基于弯沉盆参数的沥青路面动态弯沉综合修正系数

董元帅 唐伯明 刘清泉，3 朱洪洲

(1东南大学交通学院，南京210096)(2重庆交通大学土木建筑学院，重庆400074)(3交通运输部公路科学研究院，北京100088)

我国沥青路面设计体系在分析结构响应时，采用静态的参数和指标不能如实反映路面材料的力学特性，致使根据此理论计算的弯沉与实测弯沉之间存在较大的偏差.有现场实测数据表明，实测弯沉为理论弯沉的1/2或者更小，部分路段出现无法测出弯沉的情况［1］.为建立两者之间的联系，《公路沥青路面设计规范》［2］引入弯沉综合修正系数F，F为实测弯沉与理论弯沉的比值.

为了改善现行的沥青路面设计方法和指标，国内十余家单位经过多年努力于2007底初步建立了新指标体系下的动态参数设计方法，但缺少相应的路面质量验收方法.目前，国内多家单位逐步采用落锤式弯沉仪(FWD)作为验收的工具，然而FWD测试的弯沉属于动载弯沉，无法直接用于沥青路面的弯沉验收.随着FWD在国内验收的日益普及，有必要通过室内或现场试验提出基于动态参数体系的弯沉综合修正公式.

1 试验路弯沉数据的采集

室内足尺试验施工方便，既可以较好地模拟实际路面中复杂的应力环境，又可以避免土基的湿度变化对路表弯沉的影响，故本研究进行了室内足尺试验路的铺筑.在尺寸为12 m×3 m×2 m的试槽中铺筑了3种结构形式的试验路段，路面具体结构如下:

路段1 碎石土+20 cm水稳碎石+20 cm AC-20+10 cm AC-16+5 cm SMA-13;

路段2 碎石土+20 cm水稳碎石+20 cm级配碎石+10 cm AC-16+5 cm SMA-13;

路段3 碎石土+20 cm水稳碎石+20 cm水稳碎石+10 cm AC-16+3 cm SMA-13.

试验路每施工完成一层，均使用FWD进行定点弯沉检测.各结构面层顶面的中心点弯沉统计结果如表1所示.

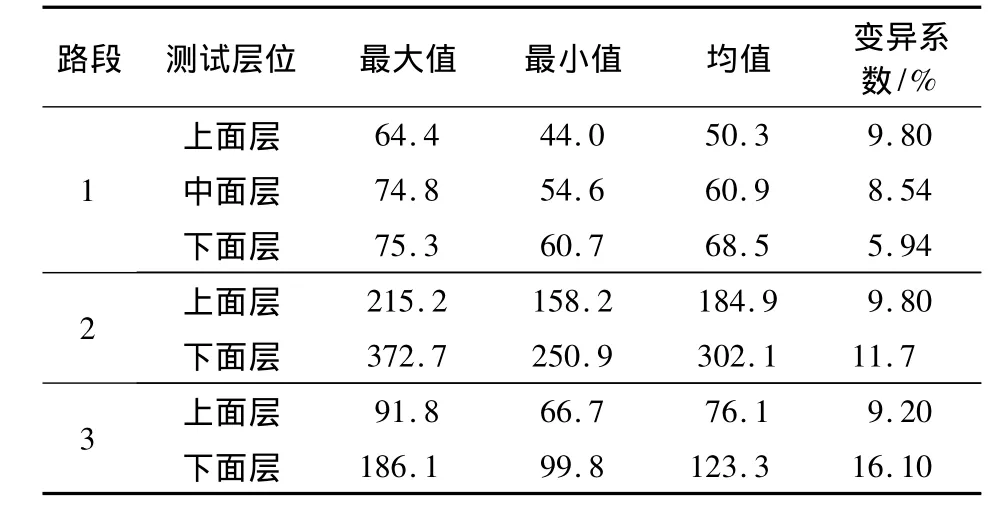
表1 足尺试验路各面层顶面中心点弯沉值 μm

2 试验路理论弯沉计算

进行温度和湿度修正后的实测弯沉值仍与理论弯沉值存在差异，影响该差异的主要原因是土基的非线性及结构层动静模量选取的问题［3］.故本研究利用ABAQUS有限元程序，采用土基和粒料层的非线性本构模型及其他结构层的动态模量计算理论弯沉.

2.1 动态模量取值

2.1.1 土和粒料

土和粒料是非线性弹-塑性材料，主要通过室内重复加载三轴试验测试其回弹模量.若不具备实验条件，可使用前人在试验基础上建立的土及粒料的动态模量经验公式估算.

本文通过颗粒分析、界限含水量及击实试验等简单的材料试验，使用文献［4-5］提出的预估方程来预估材料的回弹模量Mr:

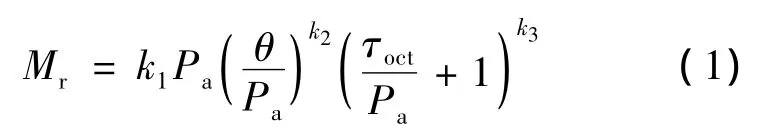
式中，θ和τoct分别为试件的体应力和八面体剪应力;Pa为大气压力;k1～k3为模型参数.

测定土基及粒料层的物性参数，代入相关公式便可得到各材料模量的计算参数，如表2所示.根据式(1)，利用有限元方法进行迭代，从而得到土基及粒料层的当量回弹模量.

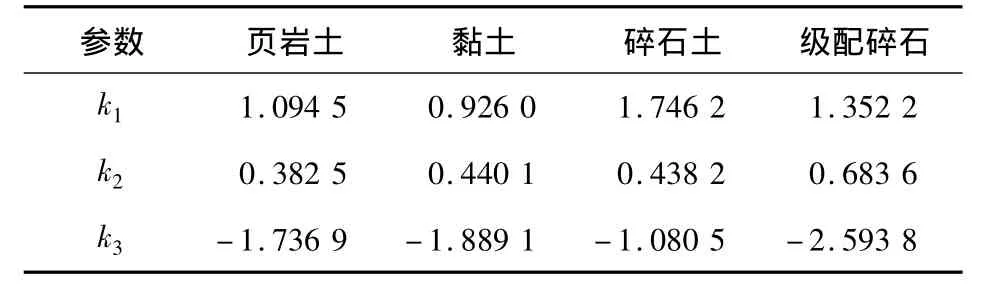
表2 三参数模型中各参数的取值

2.1.2 路面各层材料

采用SPT试验仪对沥青混合料SMA-13，AC-16和AC-20进行了动态模量测试.动态模量试验采用正弦荷载应力控制方式，试验温度为5，10，20，30，40，50 ℃.由于汽车行驶速度为 70 km/h 时对路面响应区间的作用时间大约为0.1 s，因而采用10 Hz的加载频率来测试沥青混合料的动态回弹模量.以试验路芯样的密度为依据，对旋转压实成型的试件进行了密度控制.3种沥青混合料在10 Hz下的测试结果平均值如图1所示.

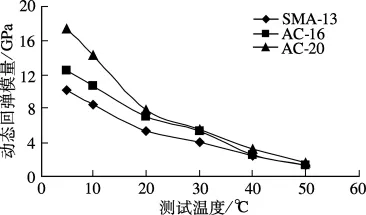
图1 3种沥青混合料动态模量测试结果平均值

由图1可明显地看出，沥青混合料是一种感温材料，不同温度下测得的动态回弹模量值有较大的差异.由于FWD测试各结构层顶面弯沉时温度并未处于标准温度(20℃)，为剔除温度对理论弯沉与实测弯沉之间差异的影响，本研究采用模量温度修正的方法，将沥青混合料的模量修正到测试温度状态下.根据图1回归建立的3种沥青混合料的温度修正公式如下:

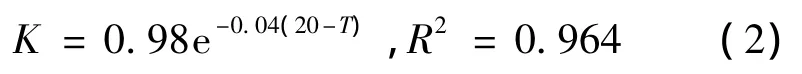
式中，K为标准温度下的沥青混合料回弹模量E20℃与任意温度T下的模量E之比.

采用同样的设备与方法测试了半刚性基层的芯样，测试结果为:上基层和下基层水稳材料动态模量的平均值分别为15.538和13.315 GPa.

2.2 有限元模型的建立

采用通用的ABAQUS有限元计算程序进行计算，计算模型模拟室内试槽的特性，尺寸采用4 m(行车方向)×3 m(宽度方向)×2 m(路基深度)，选择C3D20R单元的中等网格精度进行非线性有限元计算.边界条件为固定路基底面并限制各结构层侧面法向位移.采用与FWD荷载盘面积相当的圆形荷载，即单圆半径δ=15 cm，且垂直均布荷载为 0.7 MPa.

在现有的有限元分析软件中均未提供如式(1)所示的回弹模量本构模型，因此，在进行回弹模量计算之前，需要将该本构模型移植到有限元分析软件中，从而在计算中通过调用该模型来获得材料的应力与应变结果.本研究采用ABAQUS中Standard分析模块所提供的用户材料子程序接口UMAT 进行材料本构模型的二次开发［4，6］.

2.3 考虑材料非线性的理论弯沉计算

考虑土基和粒料层非线性的路表理论弯沉计算步骤如下:

①输入参数，在ABAQUS程序的CAE中建立三维有限元分析模型;

②通过荷载步Geostatic分析，构建路面结构中的初始应力场;

③调用UMAT用户子程序，进行三维有限元弹性非线性分析，得到路表各结点的弯沉wi.

以结构3为例，计算时需输入的材料参数如表2～表4所示.非线性有限元分析得到的路基回弹模量分布和位移场如图2和图3所示.

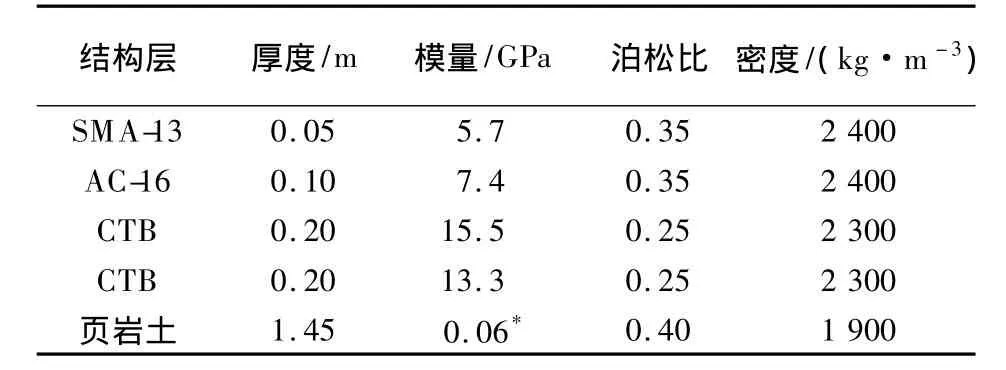
表3 沥青路面算例结构

表4 路基土非线性模型参数取值

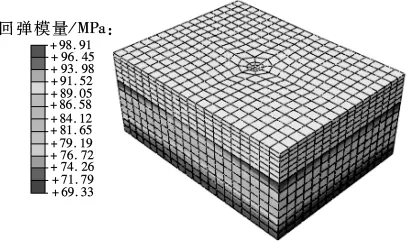
图2 土基回弹模量分布图

图3 非线性分析的总位移场

利用有限元程序计算3种结构各面层顶面的弯沉，其结果汇总于表5.由于测试下面层和中面层时温度较低，为模拟足尺试验路的实际受力状况，在计算理论弯沉时，沥青层模量进行了相应的温度修正，故结构1的下面层理论弯沉比上面层要小.

表5 计算得到的当量回弹模量及相应的路表弯沉

3 F的回归与分析

3.1 F修正值的计算

按照定义计算了沥青路面弯沉综合修正系数，并将各自结构的弯沉综合修正系数的范围及均值列于表6中.其中，F为实测弯沉与表5中理论弯沉的比值，Fj为实测弯沉与采用规范推荐模量计算得到的理论弯沉的比值.由表6可知，采用动模量计算得出的理论弯沉与FWD测试弯沉比较接近，F值的范围为0.7～1.4.而由于静态体系下的模量偏小，相应的计算弯沉较大，故大部分实测弯沉与静态理论弯沉的比值小于0.5.

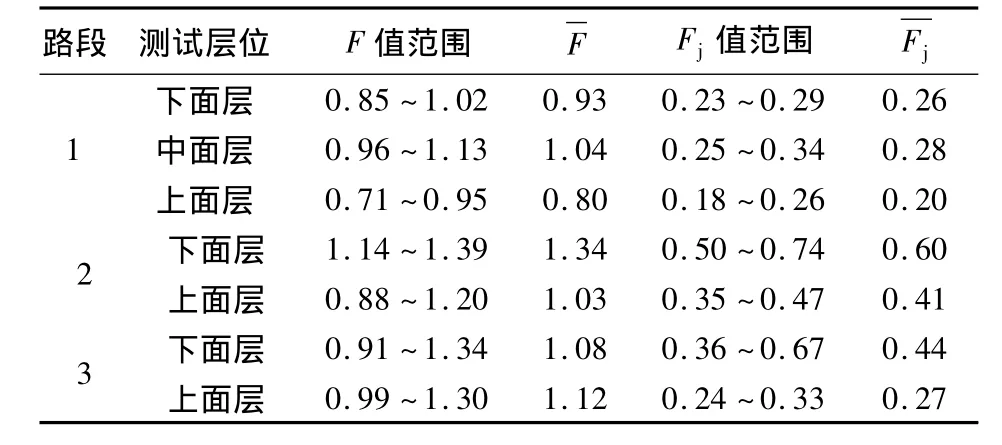
表6 不同路面组合下的弯沉综合修正系数

3.2 F修正公式的回归

文献［2］中F的修正公式只包含2个变量:实测弯沉lS和土基模量E0.lS值表征路面的整体强度，其大小主要取决于土基模量，这与公式中的变量E0产生了重复，因而考虑能否应用其他变量代替lS.作者初步考虑将面层与基层的模量比E1/E2、面层与基层的弯曲刚度比D1/D2代替lS作为回归公式的变量.

由于土基模量的非线性，其当量回弹模量受路面厚度的影响较大［3］，因此初步选定路面厚度H为F值的影响变量之一.

采用灰熵分析法选取F修正公式的变量，以F值作为评价指标，对上述5个影响因素进行显著性评价［7］，其结果如图4所示.各影响因素的灰熵关联度排序为:H＞lS＞E0≈E1/E2＞D1/D2.

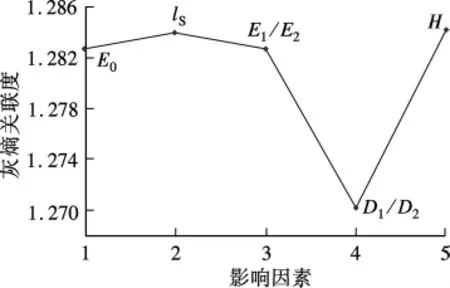
图4 不同因素的灰熵关联度

土基模量E0为F修正公式的主要影响变量，

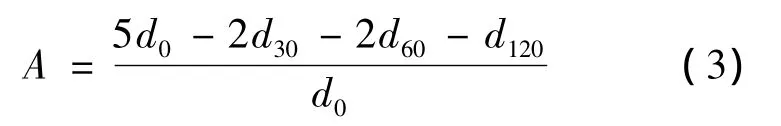
式 中，d0，d30，d60，d120为 距 荷 载 中 心 0，30，60，120 cm位置处的路面弯沉值(μm).

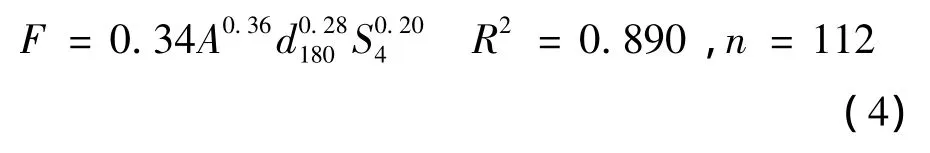
以表6中的F为因变量，以A，d180和S4为自变量，利用SPSS软件用取对数的方法将非线性回归转化为线性回归问题，从而得到了以下的F修正公式:以该变量作为判别标准，灰熵关联度大于E0的变量视为F修正公式的主要影响变量，而远远小于E0的变量则认为是非主要影响变量，故可舍去.最终选定的影响变量为:路面厚度H、实测弯沉lS、土基模量E0和面层与基层的模量比E1/E2.

若采用设计模量(E0和E1/E2)回归公式，会因设计模量与实际模量间存在的误差而影响F修正公式的精度.因而本文考虑以实测弯沉盆参数建立F修正公式.

FWD所测试的弯沉盆数据蕴含大量的信息，不同的弯沉盆参数可以表征路面整体强度、各层模量等信息［8-10］.为了利用弯沉盆参数表征上述选定的影响变量，通过对弯沉盆参数的敏感性分析［3］，将远端弯沉d180和斜率类指标S4(S4=(d45-d60)/45)代替E0和H作为回归公式的主要参数.

结合工程研究发现，用面积指标比最大弯沉指标更能准确地反映路面强度水平［11］，并且同一段路的面积指标比最大弯沉指标离散性小，更利于公式的回归.另外，通过计算可以发现，上面一层的模量与下面各层的复合模量比值越大，面积指标Ai就越大，因而本研究将面积指标Ai代替路表实测弯沉lS和 E1/E2.

为了消除试验路刚性下卧层的影响，本研究建立了一个新的面积指标A，即

3.3 F修正公式的检验

为考察式(4)的修正效果，选取室外不同结构的路表实测弯沉盆进行F修正公式的验证，并与现行沥青路面设计规范中提供的F公式进行比较.图5给出室外6段试验路的各种弯沉综合修正系数值.图中，结构1～4为半刚性基层沥青路面，其余结构为柔性基层沥青路面.

F推荐公式的回归数据来自室内试槽的测试数据，而验证数据来自室外试验路的数据，二者的数据没有相关性.通过图5可看出，采用本研究回归的公式所计算的F值与根据定义所得到的F值较为统一，二者在数值上相差不大.说明F推荐公式的验证效果比较满意，具有一定程度的适用性.

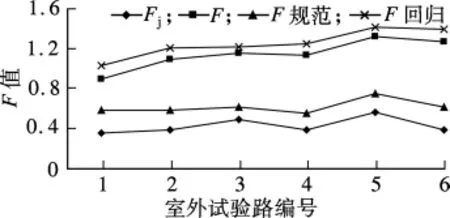
图5 试验路各种弯沉综合修正系数值比较图

3.4 验收示例

弯沉综合修正系数F主要用于新路验收，具体流程如下:

1)使用FWD采集需验收路段的弯沉盆数据.

2)根据本文建立的F修正公式编写程序，计算该路段的弯沉综合修正系数F值.

3)根据公式lt=d1/F，得到lt，并与基于动模量计算的理论弯沉lL相比较.

4)若lt＜lL，则说明该路段验收通过;反之，则不通过.

采用F推荐公式进行路表弯沉验收，与现在的验收程序略有不同.现行沥青路面设计规范以弯沉作为设计指标，在验收前便提出一个验收标准:实测弯沉小于该值，则验收通过;反之，则不通过.而本文F推荐公式的变量全部采用实测弯沉，故只有在验收结束后才会计算出F值和验收标准.这样做的好处是只有在验收结束之后才知道验收是否合格，可避免在验收过程中数据造假的行为发生.

以图5中结构1为例，利用FWD采集的弯沉盆数据代表值计算得到的弯沉综合修正系数F为1.02，lt=100.3/1.02 μm =98.3 μm ＜ lL=112.3 μm，故结构1验算通过.按规范进行验收和按本文回归的F修正公式进行验收，6条试验路全部验收通过.从而亦可说明本文建立的F推荐公式具有一定程度的适用性.

4 结论

1)采用SPT试验仪测试3种沥青混合料在不同温度下的动态回弹模量，并且根据研究的需要建立了沥青混合料模量的温度修正公式.

2)利用ABAQUS有限元程序，调用UMAT编写土基和粒料层的非线性本构模型子程序，并使用其他结构层的动态模量值来计算路表理论弯沉.FWD测试弯沉值与计算得到的弯沉值较为接近，其比值在0.7 ～1.4之间.

3)通过回归分析，得到了基于弯沉盆参数的F 修正公式，即 F=0.34A0.36d0.28180S0.204.采用室外试验路数据考察该式的修正效果，结果表明该式计算所得到的F值与根据定义所得到的F值在数值上相差不大，能适用于半刚性基层及柔性基层沥青路面.

4)根据F推荐公式编制了新的弯沉验收程序.对6条试验路同时使用规范和本文建立的方法进行验收，2种方法验收结果一致.结果表明，本文建立的F推荐公式及验收方法具有一定的适用性及可行性.

References)

［1］胡春华.沥青路面弯沉修正问题研究［D］.上海:同济大学道路与机场工程系，2005.

［2］中交公路规划设计院.JTG D50—2006公路沥青路面设计规范［S］.北京:人民交通出版社，2006.

［3］董元帅.沥青路面动态弯沉综合修正系数研究［D］.重庆:重庆交通大学土木建筑学院，2010.

［4］凌建明，罗志刚.路基与粒料层动态模量参数研究［R］.上海:同济大学交通运输工程学院，2007.

［5］AASHTO.AASHTO guide for design of pavement structures［S］.Washington DC:American Association of State Highway and Transportation Officials，2002.

［6］NCHRP.Finite element procedures for flexible pavement analysis［R］.Washington DC:Transportation Research Board，2004.

［7］董元帅，唐伯明.基于灰熵法的综合弯沉修正系数研究［J］.路基工程，2010(6):51-53.Dong Yuanshuai，Tang Boming.Research on the deflection correction coefficient based on grey entropy relation algorithm［J］.Subgrade Engineering，2010(6):51-53.(in Chinese)

［8］ASTM D5858.Guide for calculating in situ equivalent elastic moduli of pavement materials using layered elastic theory［S］.West Conshohocken，PA，USA:ASTM International，2003.

［9］ASTM D4695.Standard guide for general pavement deflection measurements［S］.West Conshohocken，PA，USA:ASTM International，2008.

［10］Ni Fujian，Zhou Lan，Ding Junfeng.Evaluation parameter of asphalt pavement with semi-rigid base based on deflection basin［C］//Transportation Research Board 89th AnnualMeeting. Washington DC，2010:01152434.

［11］Xu Bing.Assessing pavement layer condition using FWD deflection data［D］.Raleigh，NC，USA:Department of Civil Engineering，North Carolina State University，2000.