混沌映射同步的上市公司聚类分析
2011-06-06李嵩松惠晓峰
李嵩松,惠晓峰
(哈尔滨工业大学 管理学院,黑龙江 哈尔滨 150001)
股票市场是当今备受瞩目的金融市场之一,股票指数是股票市场的指示器,它是度量组成该指数的所有股票的市场平均价格水平及其变动情况的指标.因此,对构成股票指数的成分公司的聚类分析不仅具有理论意义同样也具有重要的实践意义.
聚类分析是一种多元统计分类方法,是对给定的一个有N个元素组成的数据集,构造K个分组,每一个分组就代表一个聚类,K<N[1].这种方法不必事先知道分类对象的分类结构,其基本思想是:从一批样品的多个观测指标中,找出度量样品之间或指标之间的相似程度的统计量,构成一个对称的相似性矩阵;在此基础上进一步找寻各样品(或变量)之间或样品组合之间的相似程度,按相似程度的大小,把样品(或变量)逐一归类,关系密切的归类聚集到一个小的分类单位,关系疏远的聚集到一个大的分类单位,直到所有样品或变量都聚集完毕,形成一个亲疏关系谱系图,更自然地和直观地显示分类对象(个体或指标)的差异和联系[2].当不能获得聚类所需要的一些前提信息时,采用非参数法是个有效的办法.非参数法聚类对数据结构很少做假设,它不是基于各种各样的距离的,而是基于密度的,是要在数据空间里寻找高密度区域.此外,由于聚类的数量事先没有选定,当要获取一个层次数据体系结构而并非一个固定划分时,这类方法会更适合[3-4].联动算法(凝聚和分裂)是非参数法中的一种,它输出的是显示在不同尺度下聚类解的整体层次结构树形图[5].这种联动算法中的凝聚方法从只包含一个元素的聚类出发,在每一步都合并有最小距离的2个聚类.在没有对数据的内在结构做任何假设的条件下,为了得到层次分类体系,采用了一种被称为混沌映射聚类算法[6-7]的非参数聚类方法,也就是依赖于混沌映射同步的聚类方法[8-10].混沌映射聚类算法有着广泛的应用:例如被应用在带有线粒体的DNA序列人类演化的研究方面[11];被应用在疾病映像病理脑电图记录的诊断研究中[12-13];并且还被应用在寻找地下煤矿方面[14]等.
1 混沌映射聚类算法
在混沌映射聚类算法最初被引入作为主要算法时,是将要被聚类的那些元素嵌入一个D维的特征空间里.在这个框架下,每个数据点都被看成在承载混沌映射动力学的网格上有一个对应的位置.也就是说,映射变量 xi∈[-1,1](i=1,2,…,N)被分到格子上的每个对应位置上,并且将相邻映射之间的短程相互作用看成是关于位置间距离的指数递减函数.相应在原始数据空间中的高密度区域,在静态的体系下同步映射聚类会出现.映射之间的互信息可以作为构造聚类的相似性指标,也可以用来重构分层树的一个尺度参数[15].
如果能够提供一个关于相似性(不一定必须是数学意义下所指的距离)的N×N矩阵替代所有数据信息的特征向量时,两两混沌映射聚类算法就能够很容易被实现.
当处理聚类时间模式 yi(t)时,相关系数cij(cij∈[-1,1])就是对相似度的一个自然测度,表达式为

式中:<·>表示的是在所研究的时间周期内的日平均,日平均是在整个时间序列区间内计算的.在Kullmann的研究中[16],金融时间序列之间的相关系数作为超顺磁性聚类SPC(Super paramagnetic clustering)算法[17-18]的输入信息.超顺磁性聚类算法与混沌映射聚类算法有着相近的原理,物理系统经常被用来划分非齐次铁磁模型数据.运用Potts模型,对每个数据点和相邻位置间的短程相互作用,用给定旋转状态数Si代替映射变量,用spin-spin关联函数代替相似性指标的互信息作为聚类的数据.在超顺磁的框架下,相对于数据类别联合自旋区域就会出现.Kullmann通过引入如下spin-spin强度作为相关系数Cij的函数把SPC方法推广到反-铁磁方式耦合:

式中:符号函数sgn把公司股票价格之间正(负)相关系数映射成了Potts模型自旋状态数之间正(负)的相互作用;cij是公司i和公司j之间的相关系数.考虑到以下2个原因:1)相互作用Jij应该为相似性的一个快速递增函数:为了把问题的长程信息转化成短程信息;2)值较小的相关系数是由噪音引起的,而不是那些带有信号的信息,但是又不想让这些较小的相关系数影响结果.参数(a,n)的选取应该保证超顺磁状态的存在,但是在这样的区域里面,获得的结果相对于参数(a,n)的选取并不敏感.对参数细微的调整能够更清晰地观察数据的变化,也就是说,使磁化率函数的峰值更尖锐,使他们之间的平缓变化区域更大.整偶数n用来调节相互作用的变化范围;指数项中的因子n/(n-1)用来改变相互作用函数的拐点.参数a的选取是每一个自旋的最大相关系数的平均值:
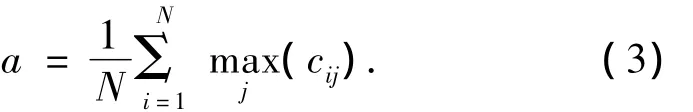
基于混沌映射动力学,金融时间序列之间的相关系数应该被映射到取值在[0,1]映射之间的正的相互作用区间.因此,式(2)自然地在cij≥0时可以进行有效运算;当cij<0时,令Jij=0.通过这种办法,就可以在相关系数为正的公司之间建立起一个带有指数增加的部分耦合映射格子.尽管并不能像全局耦合情况下那样能够找到真正的同步和相同动力状态聚类的信息,然而,在随机耦合系统下,仍然能够观察到几乎同步的映射聚类.如果只保留正的相关时间序列的相互作用,就可以得到具有相同时间行为的一组公司的几乎同步的映射形式,尽管相关公司看起来是属于不同聚类的.混沌映射可以写成如下表达式:
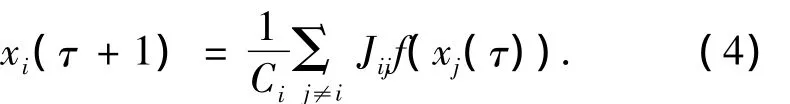

2 实证研究
2.1 样本和数据
为了使实证研究更具有代表性和说明性,实证研究数据选取了由香港恒生指数公司编写的中国内地25指数.该指数是由市值最大的25家主要营业收入或资产来自中国内地的公司组成的,是追踪在香港上市中国大型股公司表现的高投资性指标.表1显示的是组成恒生中国内地25指数的成分公司的代号及其所属行业.
选取了组成恒生中国内地25指数的全部25家成分公司的日收盘股票价格数据,数据期间为2009年1月1日至2009年12月31日,全年共开市248天,共6200个数据.

表1 恒生中国内地25指数成分公司及其所属行业Table 1 HangSeng mainland 25 index companies
2.2 计算和分析
运用混沌映射聚类算法对组成恒生中国内地25指数的全部25家成分公司进行聚类分析,所以在这里N=25.采用两两分组形式,共有N(N-1)/2=300个组.每对两两公司的相关系数cij可以通过表达式(1)计算得到,其中,Y是通过2个公司股票价格时间序列的对数变差来计算的:

式中:Pi(t)是公司i在第t天的股票收盘价格.相关系数cij的运算结果是一个25×25的对称矩阵,如表2所示.

表2 相关系数cij的部分计算结果Table 2 A portion of cij
当cij<0时,称这2个公司成反相关关系,成反相关的公司组数Nc<0的个数与总组数相比是一个相对较小的数,并且成反相关的公司的相关系数的平均值 <c>c<0几乎为零.
作为数据处理的结果,树状图被用来显示在互信息Iij取不同值时,聚类的层次结构说明如下:
1)从每个映射xi(t)中逐位提取序列Si使其满足:
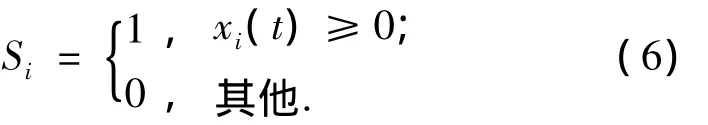
2)分别计算在整个序列中出现Si状态的概率P(Si),并相对于序列长度进行归一化,类似的,P(Si,Sj)为在序列 Si和 Sj中同时出现状态(Si,Sj)的概率.
3)计算数据熵Hi和相关熵Hij,表达式如下:

4)则互信息Iij可以表示为Iij=Hi+Hj-Hij.
互信息是映射之间关系的一种度量[19],取值在独立映射时的Iij=0和同步映射时的Iij=ln2之间.鉴于此,互信息Iij能够用作相似指标对上市公司进行分类.通过一个特定的水平集I∈[0,ln2]来分割树状图,这样就能够得到基于Iij≥I条件下的上市公司的聚类.水平集I的选取依赖于聚类解的某一稳定准则.为此,通过寻找在最大可能范围下I的稳定状态,可以使聚类熵S(I)被用来在整个层次内选择最稳定的划分方式:
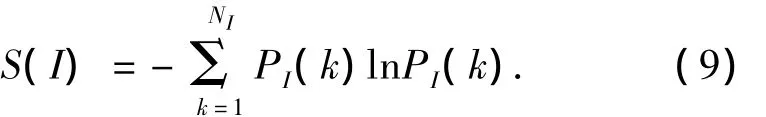
式中:PI(k)是数据属于聚类k的比例,NI为在水平集I的聚类个数.
这个模型依赖于一个参数,正的偶整数n用来调节相互作用的范围.这个参数n的最优值选取都依赖于在式(9)中不同的聚类划分情况下熵的稳定准则.一旦选取了参数n之后,聚类的所有结构体系就可以以一个树状图来显示.图1给出了在2009年组成恒生中国内地25指数的全部25家成分公司的树状图结果.其中,选取了参数n=8.

图1 恒生中国内地25指数成分公司聚类树状图Fig.1 Dendrogram of the clustering of Heng Seng mainland 25 index companies
3 结束语
在以香港恒生中国内地25指数成分中的上市公司为样本的实证研究中,通过将上市公司的股票价格间的关联程度作为该金融时间序列的相关系数,并以此相关系数作为相似性的度量指标,对上市公司进行两两模式的聚类分析.由于混沌映射间的耦合作用被引入到系数函数中,使该动力系统能够对上市公司按照相似性程度进行聚类,并得到了属于相同产业背景下的公司通常是聚类在一起的聚类结果.由于股票市场的复杂性和不确定性,无论什么方法想要准确描述上市公司的变动情况是很困难的,还有很多问题值得进一步研究.
[1]FUKUNAGA K.Introduction to statistical pattern recognition[M].San Diego:Academic Press,1990:1-25.
[2]韩江舟,葛世伦,盛永祥.1999年度沪深两市中期上市高科技公司股票聚类分析[J].华东船舶工业学院学报:自然科学版,2001,15(2):86-91.
HAN Jiangzhou,GE Shilun,SHENG Yongxiang.The clustering analysis of stock indexes of high technology companies in Shanghai and Shenzhen stock exchanges[J].Journal of East China Shipbuilding Institute:Natural Sciences,2001,15(2):86-91.
[3]ELTON E J,GRUBER M J.Modern portfolio theory and investment analysis[M].New York:J.Wiley & Sons Press,1995:36-57.
[4]BOUCHAUD J P,POTTERS M.Theory of financial risks[M].Cambridge:Cambridge University Press,1999:78-96.
[5]JAIN A K,DUBES R C.Algorithms for clustering data[M].New York:Prentice-Hall Press,1988:76-81.
[6]ANGELINI L,De CARLO F,MARANGI C,et al.Clustering data by inhomogeneous chaotic map lattices[J].Physical Review Letters,2000,85:554-565.
[7]MANRUBIA S C,MIKHAILOV A S.Mutual synchronization and clustering in randomly coupled chaotic dynamical networks[J].Physical Review E,1999,60:1579-1589.
[8]KANEKO K.Relevance of dynamic clustering to biological networks[J].Physica D:Nonlinear Phenomena,1994,75:55-73.
[9]KANEKO K.Clustering,coding,switching,hierarchical ordering,and control in a network of chaotic elements[J].Physica D:Nonlinear Phenomena,1990,41:137-172.
[10]KANEKO K.Spatiotemporal chaos in one-and two-dimensional coupled map lattices[J].Physica D:Nonlinear Phenomena,1989,37:60-82.
[11]MARANGI C,ANGELINI L,MANNARELLI M.Clustering mtDNA sequences for human evolution studies[J].Modelling Biomedical Signals,2001,21:196-208.
[12]BELLOTTI R,CERELLO P,TANGARO S.Distributed medical images analysis on a grid infrastructure[J].Future Generation Computer Systems,2007,23(3):475-484.
[13]BELLOTTI R,De CARLO F,STRAMAGLIA S.Chaotic map clustering algorithm for EEG analysis[J].Physica A:Statistical Mechanics and its Applications,2004,334(1):222-232.
[14]ANGELINI L,De CARLO F,MARANGI C.Chaotic neural network clustering:an application to landmine detection by dynamic infrared imaging[J].Optical Engineering,2001,40(12):2878-2889.
[15]ANGELINI L,de CARLO F,MARANGI C,et al.Clustering data by inhomogeneous chaotic map lattices[J].Physical Review Letters,2000,85:554-565.
[16]KULLMANN L,KERTESZ J,MANTEGNA R N.Identification of clusters of companies in stock indices via Potts super-paramagnetic transitions[J].Physica A:Statistical Mechanics and its Applications,2000,287(3):412-419.
[17]GETZ G,LEVINE E,DOMANY E.Super-paramagnetic clustering of yeast gene expression profiles[J].Physica A:Statistical Mechanics and its Applications,2000,279(1):457-464.
[18]BLATT M,WISEMAN S,DOMANY E.Superparamagnetic clustering of data[J].Physical Review Letters,1996,76:3251-3254.
[19]SOLE R V,MANRUBIA S C,BASCOMPTE J.Phase transitions and complex systems simple,nonlinear models capture complex systems at the edge of chaos[J].Complexity,1996,13:13-26.
