平流层飞艇运动分析与仿真

胡国昌，吴美平

(国防科技大学机电工程与自动化学院，湖南长沙410073)

由于平流层的战略地位以及现代科技的进步，平流层飞艇成为近年来各国研究热点［1］．飞艇在高空执行特定任务(如侦察、监视、通讯等)需要其能够自主控制以及自主运行．由于飞艇具有与飞机不同的结构特点，因此，在设计控制系统时，需充分掌握飞艇的运动特征．

文献［2-5］采用牛顿法建立了平流层飞艇非线性动力学模型，而文献［6-8］采用拉格朗日法也得到了同样的结果．以此为基础，文献［9-10］进行了稳定性和能控性分析，但只研究了在确定参数条件下的局部能控性，没有考虑到飞艇运行中参数易变化的特点．文献［11-12］研究了飞艇的运动模态和飞行特点，但其对象为低空飞艇，高空飞艇的情形如何有待进一步分析．总体来讲，目前的文献没有针对平流层飞艇运动特性从理论上进行较为详细地分析，而且只研究了局部能控性，运动模态的分析也较为简单．基于以上背景，引入大系统中的结构能控性方法［13］，综合分析飞艇稳定性、能控性和运动特性，并进行相应的仿真研究，以期对飞艇控制策略的设计提供一定的指导．

1 飞艇动力学模型

1．1 飞艇模型结构

本文研究的平流层飞艇假设为软式飞艇，呈椭球体外形，尾翼采用“+”结构布局，并且装有升降舵和方向舵控制舵面，尾部配备推进装置，底部为吊舱，其两侧分别安装涵道风扇，用于实现矢量推进．飞艇整体布局如图1所示．

1．2 非线性动力学模型及其线性化

由于运行环境和副气囊充放气的影响，飞艇重心位置是变化的，为便于描述其运动，艇体坐标系原点选为体积中心．

为得到有意义的飞艇运动方程和分析其运动特性，采用下列基本假设:

1)在平流层中飞行的飞艇近似为刚体，忽略其弹性效应;

2)飞艇的体积中心与浮心重合;

3)飞艇具有对称平面 ，且重心在对称面内，惯量积．采用拉格朗日法得到飞艇六自由度非线性动力学模型［6-8］:

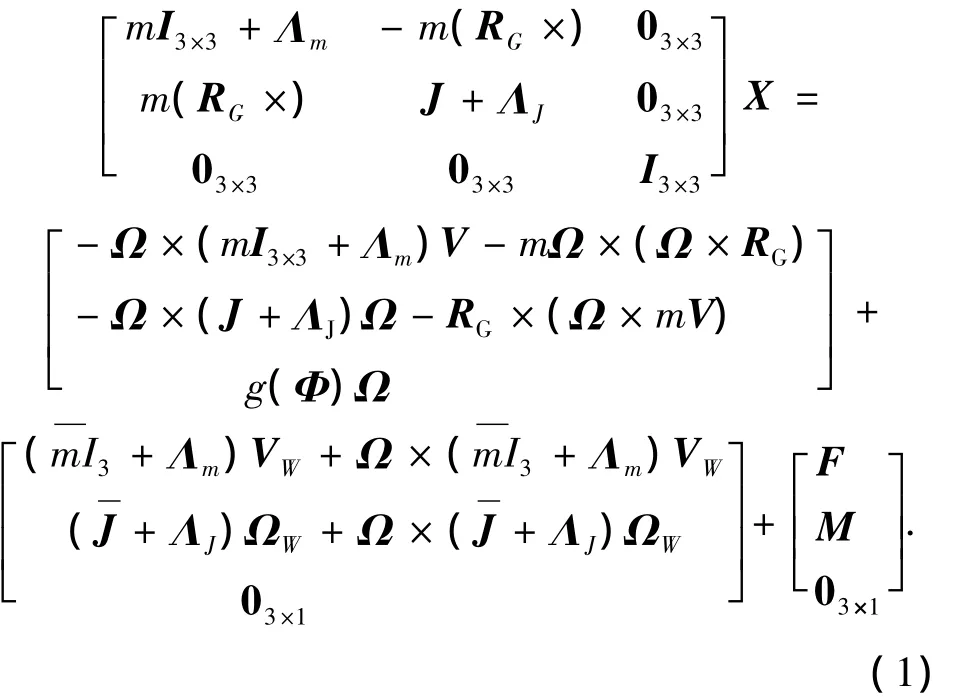
将式(1)写为标准状态方程形式:

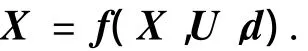
式中:f(·)为矩阵形式的非线性函数，控制输入U=［P FTVTFTVDμyδeδr］T，P 为尾部推进器推力，FTVT、FTVD分别为左右风扇推力之和与之差，μy为风扇绕飞艇横轴的转角，δe、δr分别表示升降舵偏角、方向舵偏角，d为外界干扰，包括风的作用．各参数的意义以及作用力的表达式详见文献［3］．

类似于飞机等飞行器，飞艇的运动可以分为基准运动和扰动运动．基准运动指各运动参数完全按照预定规律变化的运动，通常为配平的定常飞行．扰动运动是飞行中受到外界干扰而偏离基准运动的运动．采用小扰动线性化方法对飞艇动力学模型进行线性化，即假设扰动运动相对于基准运动为小偏量，从而略去高阶小项使得运动方程为线性的．该方法分2步实现:1)设定基准运动，求取相应的控制量．本文假定基准运动设为无倾斜、无侧滑且迎角为零的等速水平直线飞行，2)对原运动方程在基准运动情况下进行一阶泰勒展开，即得到飞艇运动线性近似方程:

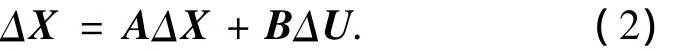
在本文假设条件下，飞艇线性近似运动方程可以解耦为纵向和横侧向2个方程:

2 动力学模型稳定性分析

2．1 运动稳定性及其判定

稳定性讨论系统运动状态受初始扰动后的动态特性，即研究初值的微小扰动是否会引起系统状态轨线无限偏离的问题，是在没有控制作用时系统自身固有的性质．由稳定性的定义可知［14］，求出系统(数学模型为微分方程组)的通解后，其稳定性是比较容易判定的．但是形如式(1)的非线性系统很难求出解析表达式，因此难以判定其稳定性．一种解决办法是采用李亚普诺夫第二方法;另一种方法则是线性近似法．李亚普诺夫第二方法需要找到李亚普诺夫函数，这在非线性系统中是非常困难的．因此本文采用线性近似法，其思路为将非线性系统线性化，进而根据下面引入的2个定理判断原系统的稳定性．

定理1 如果线性近似系统的特征方程没有零实部的根，则非线性系统零解稳定性与此线性近似系统的稳定性相一致［14］．

定理2 如果线性近似系统的特征方程有零实部的根，则非线性系统零解的稳定性不能由此线性近似系统的稳定性确定，此种情形称为临界情况，稳定性与非线性项有关［14］．

2．2 飞艇运动稳定性

通过上一小节的推导，飞艇运动的稳定性可由线性近似系统(式(2))进行判断，而线性近似系统的稳定性可直接通过矩阵A的特征值进行判定．

由小扰动线性化过程可知，基准运动不同则线性近似方程也不同．飞艇的基准运动为等速水平直线飞行，前向速度(以下简称平衡飞行速度ue)影响特征值．图2和表1为平衡飞行速度1～45 m/s时纵向运动特征值的变化情况．可知飞艇纵向运动的4个特征值:一个非常接近虚轴的负实根λL1，一个绝对值稍大的负实根λL2，以及一对正实部共轭根λL3、λL4．由于存在实部为正的特征值，飞艇纵向运动不稳定．同时，随着平衡飞行速度增大，λL1变化很小，λL2向负方向变化较小，而 λL3、λL4向正方向变化较大，因此纵向运动稳定性进一步变差．

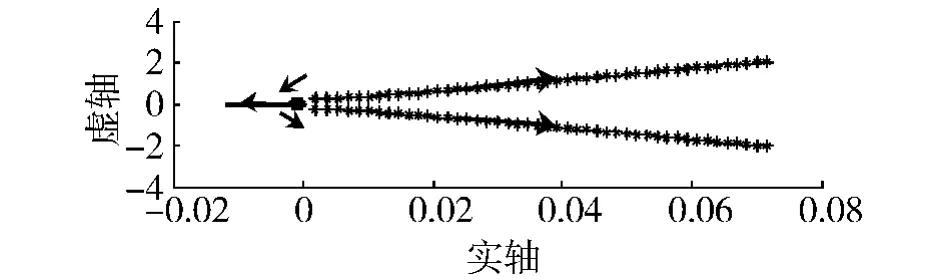
图2 纵向特征值Fig．2 longitudinal eigenvalue

图3和表2为平衡飞行速度1～45 m/s时，横侧向运动特征值变化情况．飞艇横侧向运动特征值由2 对共轭特征根λS1、λS2和 λS3、λS4组成．由于存在实部为正的特征值，飞艇横侧向运动不稳定．随着平衡飞行速度增大，λS1、λS2由正实部逐渐变为负实部，并且负实部开始远离虚轴而后又向虚轴靠近，而λS3、λS4总体上向正方向变化较大，因此纵向运动稳定性进一步变差．

图3 横侧向特征值Fig．3 Latitudinal eigenvalue

表1 Ue变化时的纵向特征值Fig．1 longitudinal eigenvalue of varying Ue

表2 Ue变化时的横侧向特征值Fig．2 latitudinal eigenvalue of varying Ue

综上所述，飞艇的纵向和横侧向运动均不稳定，即飞艇运动是不稳定的．

2．3 运动模态

飞艇运动可看成是各个特征值相应运动模态的一个线性组合，特征向量和初始条件的影响体现于不同运动模态的“权重”上［15］．由前一节的讨论知:纵向运动分为3个运动模态;而横侧向运动含有2个运动模态．同一个运动模态在相同初始条件时，由各特征向量相对大小可知相应运动参数表现的强弱．为了解各个运动模态，将特征向量进行如下处理［8］:

1)进行无量纲化处理，即将线速度对应的特征向量除以平衡飞行速度Ue，角速度对应的特征向量除以Ue/(VB)1/3(其中VB为飞艇体积)，而角度对应的特征向量不变．

2)选定幅值最大特征向量，除以其幅值，使其为单位量，其他的特征向量也除以这一幅值．

3)将2)所得的特征向量画在图中．

算例:取平衡飞行速度为18 m/s，则纵向特征值为:0．028 4-0．826 1i、0．028 4+0．826 1i、-0．004 6 和 -0．001 0;横侧向特征值为:0．041 7+0．774 0i、0．041 7-0．774 0i、-0．009 1+0．525 0i和-0．009 1-0．525 0i．图 4 和图 5 为经过以上处理得到的纵向和横侧向特征向量图(共轭特征值只画出实部为正的相应的特征向量)．

从图4可知:纵向运动分为摆动、缓慢阻尼和快速阻尼3个运动模态，分别对应(a)～(c)3个子图，摆动模态主要由俯仰角速度体现，是一不稳定模态;快速阻尼模态则由前向速度体现;缓慢阻尼模态主要体现在俯仰角变化上．从图5易知:横侧向运动包含偏航振荡和滚动衰减2个模态，分别由(a)～(b)个图体现，其中偏航振荡模态是发散的，在偏航角速度中体现得最明显;而滚动衰减模态是稳定的，主要在滚动角速度中体现．同时横侧向的2种模态有一定的耦合关系．

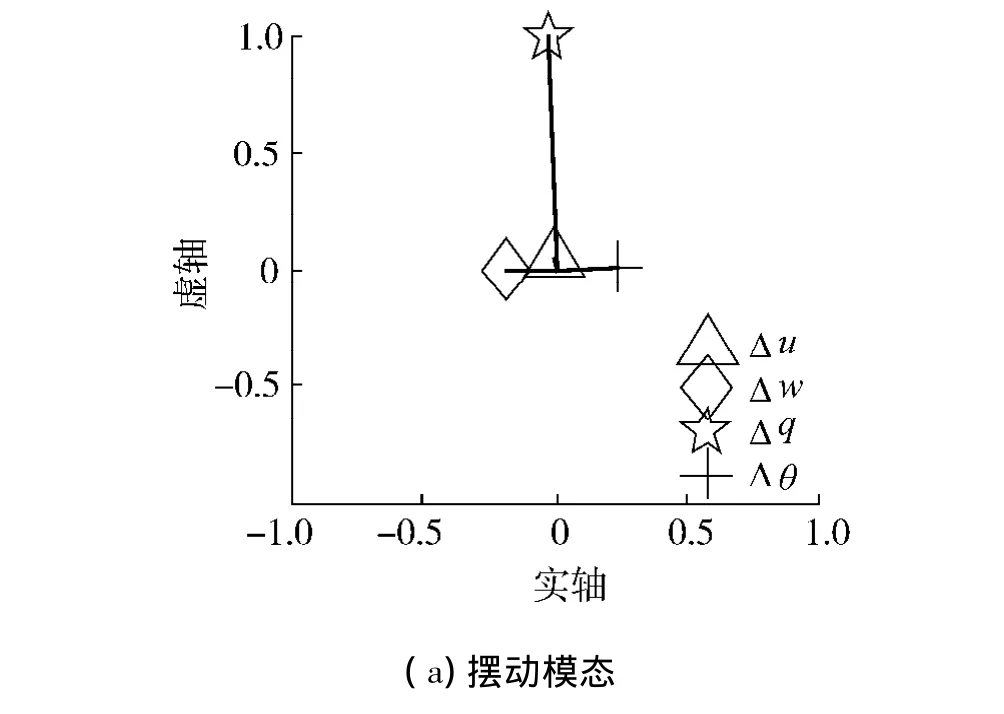
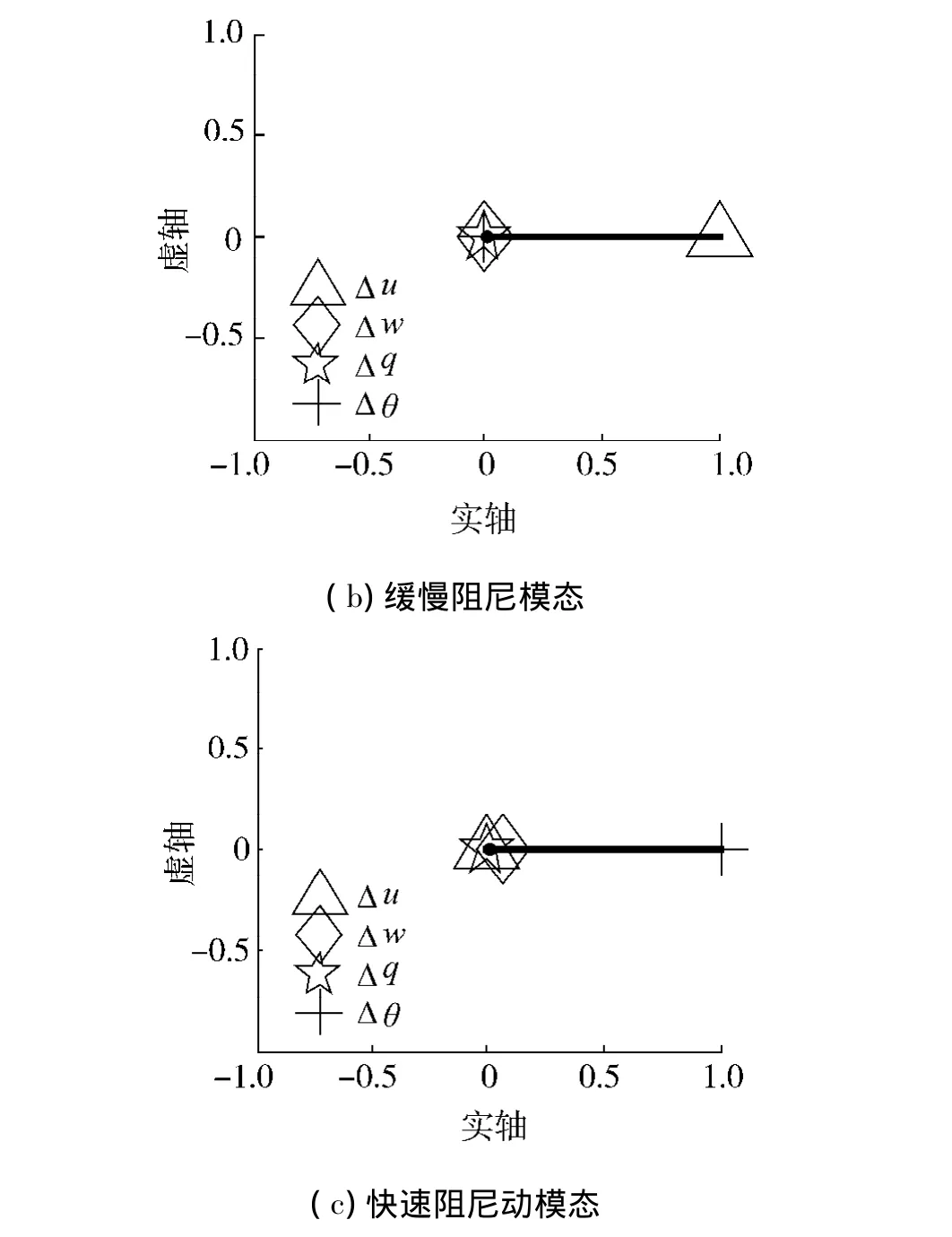
图4 纵向特征向量Fig．4 Longitudinal eigenvector

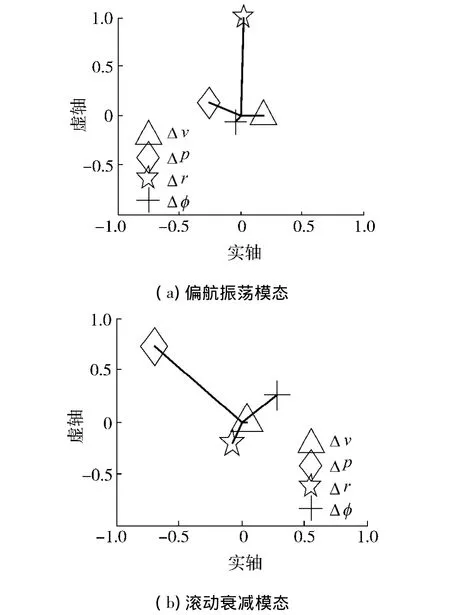
图5 横侧向特征向量Fig．5 Latitudinal eigenvector

3 动力学模型结构能控性

飞艇动力学模型是一个典型的非线性系统，而非线性系统的全局能控性往往难以衡量，因此常研究其在某一工作点附近的能控性(即局部能控性)．局部能控性的判定只能在参数完全确定情况下进行，而平流层飞艇运行中自身参数易变化，因此需实时对其进行判断，这是费时而不必要的工作．所以，本文参考大系统理论的结构分析方法，研究其结构特征及结构能控性，从而克服局部能控性判断的不足．首先引入一些相关定义和定理．

针对式(2)描述的系统，设矩阵A、B中有些元素固定为零元素(由系统实际结构参数决定的)，另一些元素不确定，可以任意取值．

结构能控性:若(A，B)有一个在通常意义上能控的结构等价对，则称(A，B)结构能控．

r型矩阵:若一个n×m矩阵A，对于满足不等式m-r≤k≤m的某个数k，含有(n+m-k-r+1)×k零子矩阵，则称矩阵A是r型的，记作form(r)．

定理3 对于系统(A，B)，扩展的能控性矩阵C有form(n2)，n为A的维数，则系统不能控．否则系统能控［13］．

考虑平流层飞艇动力学模型线性近似以后的纵向和横侧向的结构能控性，其扩展能控性矩阵均不为form(n2)，由定理三知飞艇运动是结构能控的．

4 仿真分析

根据以上对飞艇的动力学模型的分析，研究其在扰动和控制作用下的运动性能．

4．1 扰动响应

由于垂直方向和侧向初始速度扰动较为常见，因此本文讨论飞艇非线性和线性近似模型对这2种初值扰动的响应．仿真条件:初始高度 h0=21 300 m，初始速度u0=18 m/s，其余运动参数初始值为零．

图6(a)和(b)分别为非线性和线性近似模型存在Δw的扰动情况下，各运动参数响应曲线．由于横侧向运动参数的响应为零，因此图中没有示出．由图可见，运动参数 u、w、q、θ都出现振荡，并且逐渐发散，体现了纵向运动不稳定的特点．扰动越大，响应也越大．按照2．3节对各运动参数进行相应的无量纲处理方法，则图6同样能得到俯仰角速度最能体现摆动模态的结论．相同扰动量作用下，同一运动参数在线性近似模型比在非线性模型中的响应更大，这是由于线性化误差引起的．

图6 等速直线平飞对初始扰动Δw的响应Fig．6 Response of the airship to initial disturbance of Δw

图7(a)和(b)分别为非线性和线性近似模型在存在Δv的扰动时各状态变量响应曲线．由图可见，运动参数均出现明显振荡，并且很快发散，体现了横侧向运动的不稳定特性．在非线性模型中，虽然只有横向扰动，但是由于横侧向和纵向运动的耦合，使得纵向运动参数也不为0，而且均振荡和发散．比较图7(a)和图7(b)，在相同扰动量作用下，线性近似模型中运动参数比非线性模型中的响应更大，这是由于存在线性化误差的原因．图(a)中的φ、ψ发散很快，主要是由于纵向和横侧向运动耦合，交叉影响的缘故．对图中各运动参数进行相应的无量纲处理，可知横侧向的振荡发散模态在偏航角速度中体现得最为明显．

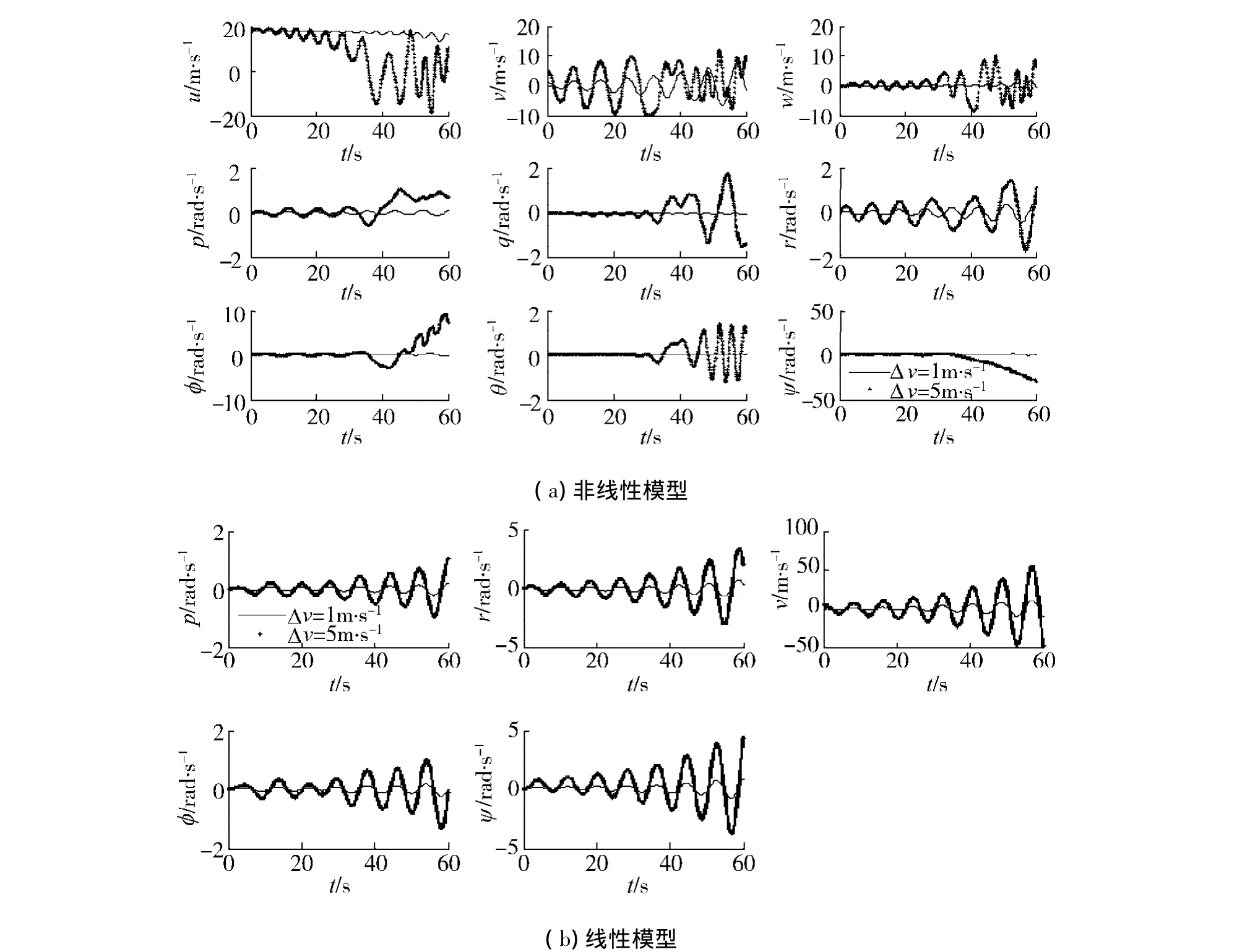
图7 等速直线平飞对初始扰动Δv的响应Fig．7 Response of the airship to initial disturbance of Δv

综上所述可知，飞艇运动是不稳定的．摆动模态在纵向运动各参数中均有明显的体现，而2种阻尼模态体现得不明显，这是由于它们的时间常数大，被摆动模态掩盖了．偏航振荡模态在横侧向运动参数中得到了明显的体现，由于该模态造成各运动参数很快发散，因此滚动振荡模态体现得不太明显．

4．2 控制作用响应

下面分别就升降舵、方向舵和主推力对系统的作用进行分析，其仿真条件同4．1节．

图8(a)和(b)分别为非线性和线性近似模型存在升降舵偏转的情况下，各运动参数响应曲线．由于横侧向运动参数未受影响，因此图8(a)中没有示出．从图中可知，等速直线平飞时，升降舵正向偏转，u、w、q、θ很快出现振荡，飞艇抬头向上飞行．并且易知，升降舵偏转越大，振荡幅度越大．同一运动参数在相同控制量作用下，线性化模型与非线性模型的响应幅值大小相差不大，说明线性化误差对控制的影响较小．

图8 等速直线平飞对控制作用δe的响应Fig．8 Response of the airship to initial disturbance of δe

图9为存在方向舵偏转的情况下，飞艇非线性和线性近似模型各运动参数响应曲线．由图易知，等速直线平飞时，方向舵偏转，飞艇横侧向和纵向运动参数均振荡，但横侧向参数振荡更剧烈些，同时幅度更大．方向舵正向偏转，飞艇低头减速飞行．方向舵偏转越大，振荡幅度越大．在相同控制量作用下，线性化模型比非线性模型的响应幅值小，这是因为非线性模型中纵向和横侧向耦合影响所致．

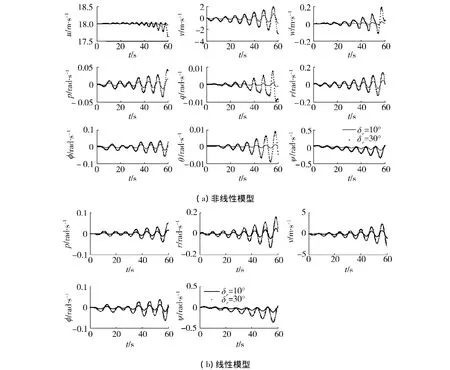
图9 等速直线平飞对控制作用δr的响应Fig．9 Response of the airship to δr

对水平匀速直线飞行的飞艇施加主推力，其运动参数变化如图10所示．由于主推力的方向始终在纵向平面内，因此施加主推力不会影响横侧向运动，而前向速度振荡地增大．主推力作用方向不经过飞艇重心，造成俯仰角的振荡，从而产生垂直方向的速度．主推力对线性近似模型的控制作用与对非线性模型的控制作用大致相当，线性化较为合理．

图10 等速直线平飞对控制作用P的响应Fig．10 Response of the airship to initial disturbance of P

综上所述，控制机构能对飞艇运动很快产生影响，但是由于飞艇运动自身不稳定，需要一定的控制算法才能保证其控制性能指标．飞艇纵向和横侧向可以进行解耦控制，升降舵和主推力进行纵向运动控制，而方向舵控制横侧向运动．

5 结束语

掌握平流层飞艇运动特性是对其进行控制的基础和前提．本文以某平流层飞艇动力学模型为基础，分析了稳定性，讨论了运动模态，同时研究了结构能控性．在此基础上，对初值扰动和控制作用下飞艇的运动特性进行了仿真分析，得出如下主要结论:飞艇运动不稳定，纵向的摆动模态以及横侧向偏航振荡模态占支配作用;飞艇动力学系统结构能控，升降舵、主推力影响纵向运动参数，方向舵控制横侧向运动参数;对非线性动力学模型进行线性化进而解耦为纵向和横侧向2个子系统是合适的;线性化误差对初值扰动的响应影响较大，而对控制作用的影响很小．

［1］曹秀云．近空间飞行器成为各国近期研究的热点(上)［J］．中国航天，2006，6:32-35．

［2］KHOURY G A，GILLET J D．Airship technology［M］．London，Cambridge University Press，1999:58-70．

［3］MUELLER J B，PALUSZEK M A．Development of an aerodynamic model and control law design for a high altitude airship［C］//．AIAA Unmamed Unlimited Conferene．Chicago，USA，2004．

［4］欧阳晋．空中无人飞艇的建模与控制方法研究［D］．上海:上海交通大学，2003:23-78．

OUYANG Jin．Research on modeling and control of an unmanned airship［D］．Shanghai:Shanghai Jiao Tong University，2003:23-78．

［5］王海峰，宋笔锋，钟小平．飞艇运动建模与仿真验证［J］．飞行力学，2009，27(1):31-35．

WANG Haifeng，SONG Bifeng，ZHONG Xiaopin．Modeling and simulation verification of motion for an airship［J］．Flight Dynamics，2009，27(1):31-35．

［6］AZINHEIRA J R，MOUTINHO A．Influence of wind speed on airship dynamics［J］．AIAA Journal of Guidance，Control and Dynamics，2002，25(6):1116-1124．

［7］AZINHEIRA J R，MOUTINBO A．Erratum-influence of wind speed on airship dynamic［J］．AIAA Journal of Guidance，Control and Dynamics，2008，31(2):443-444．

［8］MOUTINHO A B．Modeling and nonlinear control for airship autonomous flight［D］．Lisbon:University of Lisbon，2007:33-78．

［9］王晓亮，单雪雄．飞艇稳定性和能控性分析［J］．计算机仿真，2005，22(8):40-44．

WANG Xiaoliang，SHAN Xuefei．Analysis of stability and controllability of airship［J］．Computer Simulation，2005，22(8):40-44．

［10］LI Y W，MEYER N．Modeling and simulation of airship dynamics［J］．Journal of Guidance，Control，and Dynamics，2007，30(6):1691-1700．

［11］欧阳晋，屈卫东，席裕庚．轻于空气的飞艇纵向运动的分析及仿真［J］．上海交通大学学报，2003，37(6):961-963．

OUYANG Jin，QU Weidong，XI Yugeng．Longitudinal motion analysis and simulation for Lighter-than-air(LTA)airship［J］．Journal of Shanghai Jiao Tong University，2003，37(6):961-963．

［12］LIU Y，HU Y M，WU Y L．Stability and control analysis based on airship dynamic modeling［C］//Proceedings of the IEEE International Conference on Automation and Logistics．Jinan，China，2007:2744-2748．

［13］王翼，张朝池．大系统控制:方法和技术［M］．天津:天津大学出版社，1993:77-100．

［14］胡跃明．非线性控制系统理论与应用［M］．北京:国防工业出版社，2005:153-170．

［15］郑大钟．线性系统理论［M］．2版．北京:清华大学出版社，2002:98-101．