利用场路结合方法分析磁轴承悬浮力

王大朋， 王凤翔

(沈阳工业大学电气工程学院，辽宁 沈阳 110870)

0 引言

在高速电机系统中，普通的机械轴承存在着摩擦和磨损，而且需要润滑系统，由此会带来使用寿命下降及润滑油污染等一系列问题。磁轴承是利用电磁力使转子悬浮在定子中转动，具有无机械摩擦和磨损、无需润滑、能耗低、噪声小、寿命长等优点，特别适合于在高速电机等领域应用［1－2］。

磁轴承一般分为主动磁轴承、被动磁轴承和混合磁轴承三类［3－5］。因为主动磁轴承更容易控制，且应用技术比较成熟，所以目前获得实际应用的主要是主动式磁轴承。由于磁轴承系统的复杂性，目前对磁轴承的悬浮力分析一般以电路和磁路分析为基础，忽略磁饱和及漏磁等影响，在工作点附近运行范围内进行线性化处理，很少采用基于磁路耦合或场路分析结合的方法对悬浮力进行分析［6－11］。

为了能够更准确地计算磁轴承的悬浮力，本文首先基于磁路分析推导了主动式径向磁轴承的悬浮力线性化模型。然后利用有限元法分析了磁轴承在不同偏置电流和转子位移下的悬浮力特性曲线，确定了最佳偏置电流，对其线性化悬浮力模型的位移刚度系数和电流刚度系数进行修正，并建立了超出线性化范围悬浮力的非线性模型。最后对所建立的磁轴承悬浮力模型进行了实验验证。

1 基于电路和磁路分析的径向磁轴承悬浮力线性化模型

主动式径向磁轴承类似于一台电机，定子通常采用8个齿槽，又分为两种磁路结构，如图1所示。图1(b)所示磁路结构可以消除垂直和水平方向悬浮力控制绕组电流磁场的相互影响，有利于悬浮力的解耦控制，是本文所研究的磁轴承结构。

图1 径向磁轴承结构Fig.1 Structure of radial magnetic bearing

为了研究的方便，本文对单自由度转子的受力分析。单自由度(X方向)系统结构如图2所示。

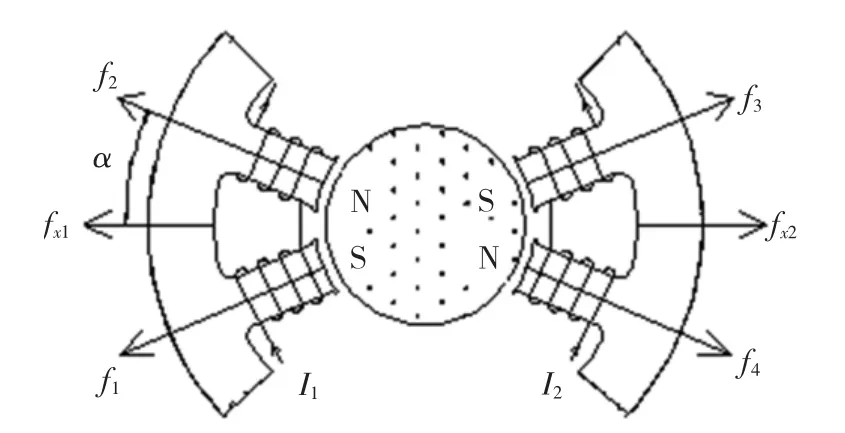
图2 单自由度磁轴承示意图Fig.2 Schematic diagram of magnetic bearing with single degree of freedom

由图2可看出，当定子左右控制绕组分别通入电流I1和I2后，转子承受的X方向上的合力为

当不计铁心磁阻并假设定子与转子表面之间的气隙均匀为δ0、磁极面积为S、真空磁导率为μ0、每个磁极线圈匝数为N/2和通电电流为I时，考虑到磁极与垂直方向的夹角α后，转子在X方向左右受力分别为

当转子沿X轴的位移为x时，令K=μ0SN2，则

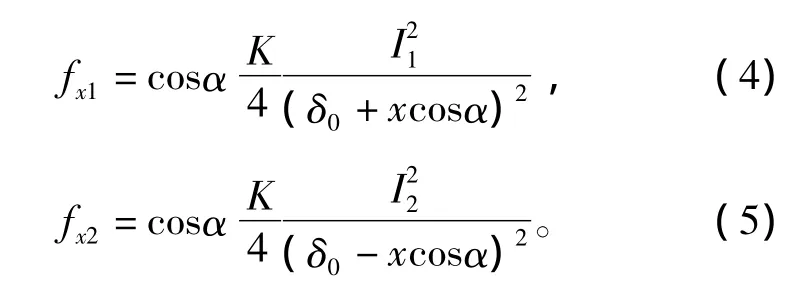
通常悬浮力采用差值控制方式，即左右悬浮力控制绕组一个通以偏置电流ib与控制电流ix之和，而另一个则通以偏置电流ib与控制电流ix之差的电流，因此转子在X方向上的受力可表示为

考虑到正常悬浮的转子处于平衡位置附近，此时 xcosα≪δ0，则式(6)可以化简为

因此转子在X方向上的稳态受力可表示为

其中kxi和kxx分别为电流刚度和转子偏移刚度，计算公式为

2 基于磁场分析的径向磁轴承悬浮力特性

上一节推导的是悬浮力的一种近似的线性表达式，本节将采用有限元磁场分析方法，计算不同定子绕组控制电流和不同转子偏移下的悬浮力特性，以便获取更为准确的悬浮力模型。所分析的径向磁轴承系统参数为:定子内径64.5 mm;定子外径75 mm;定子齿宽14 mm;转子外径64 mm;单边气隙长度0.25 mm;轴向长度20 mm;线圈匝数130匝。

为了分析方便，采用单独改变转子偏移和控制电流的情况进行分析。在单独改变转子偏移位置的分析中，控制电流ix被设置成0，对于每个给定转子偏移x，改变偏置电流ib(偏置电流变化范围为1.0～4.5 A)，分别进行磁场分析计算转子所承受的悬浮力。采用类似的方法，可以计算单独改变控制电流时的悬浮力。图3为在不同的偏置电流下，悬浮力与转子偏移的关系曲线，而图4则为不同转子偏移下悬浮力与偏置电流的关系曲线。

在图3中可以看到当偏置电流ib≥3 A时，悬浮力－转子偏移曲线变得接近了，随着偏置电流的进一步加大，在不同位置的悬浮力反而开始降低了，这是由于磁路中的磁饱和引起的。在图3中也可以看到在偏置电流ib≤3 A的情况下，当转子位置x≥0.1 mm时，悬浮力－转子偏移曲线的非线性情况变得明显了。在图4中，可以看到当转子偏移位置ix≥0.125 mm时或偏置电流ib≥2.5 A时，期望的力与偏置电流的平方关系不存在了，这是也是由于磁饱和效果造成的。

图3 不同偏置电流下悬浮力与转子偏移的关系(控制电流ix=0)Fig.3 Levitation forces versus rotor displacements for different bias currents(control current ix=0)

图4 不同转子偏移下悬浮力与偏置电流的关系(控制电流ix=0)Fig.4 Levitation force versus bias current for different rotor displacements(control current ix=0)

图5是在固定转子偏移(x=0)时不同偏置电流下悬浮力与控制电流的关系曲线。在磁轴承的实际应用中为了避免悬浮力的跳变，控制电流一般不超过偏置电流，故图中对于不同的偏置电流悬浮力曲线具有不同的长度。由图5可以看出，当偏置电流和控制电流大于2.5 A时，悬浮力与控制电流呈非线性关系。

图5 不同偏置电流下悬浮力与控制电流ix的关系(转子偏移x=0)Fig.5 Levitation force versus control current for different bias current(rotor displacement x=0)

综合以上两种情况的分析结果，可以选择磁轴承偏置电流为2.5 A，线性化模型的适用范围为|x|≤0.1 mm，|ix|≤2.5 A。

3 磁轴承悬浮力线性化模型系数的修正

由于解析法所得到的线性化模型的两个系数是转子在平衡点附近的分析结果，同时在解析法的分析中忽略了转子和定子的磁阻影响。为了提高悬浮力线性化模型的精确度，可以利用磁场分析结果，对于线性化模型表达式(8)中的电流刚度和转子偏移刚度系数进行修正。

偏置电流 ib=2.5 A，转子偏移 x不大于0.1 mm，控制电流不大于偏置电流时，由有限元软件计算所得的悬浮力数据如表1所示，特性曲面如图6所示。

表1 利用有限元计算所得的悬浮力数据Table 1 The data of levitation force by FEA element

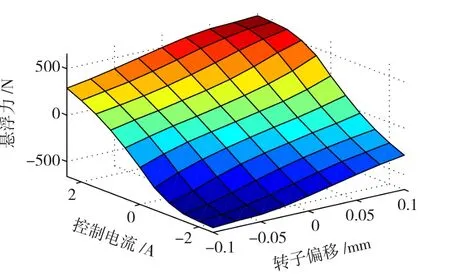
图6 悬浮力与转子偏移和控制电流的关系Fig.6 Relationship between levitation force，rotor displacement and control current

在图6中可以看到悬浮力与转子位置和控制电流的关系除了在(－2.5 A，－0.1 mm)和(2.5 A，0.1 mm)点附近接近一个平面，可以用线性化模型来表达悬浮力与转子偏移和控制电流的关系为

因为磁轴承控制器的调节作用，磁轴承一般不工作在(－2.5 A，－0.1 mm)和(2.5 A，0.1 mm)点附近，所以采用表2中灰色部分的数据，利用最小二乘法对式(11)中的转子偏移和控制电流刚度系数进行估计，估计所用公式为

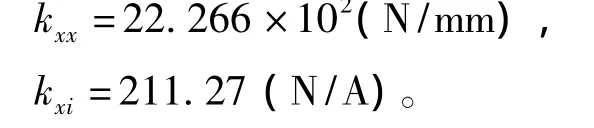
而由电路和磁路分析得到的线性化模型(8)和式(9)计算结果为

可以看出利用有限元磁场分析得到的结果与利用磁路分析所得到的结果有所不同，显然采用磁场分析所得到结果具有较好的精确度。

4 磁轴承线性化区外的悬浮力模型分析

在磁轴承正常工作时，一般工作在线性化模型的适用范围之内，但是在磁轴承起浮或者受到较大扰动力冲击时，有可能超出正常的线性化模型的范围，所以有必要对线性化模型适用范围外的悬浮力进行分析。

利用有限元法对线性化模型适用范围外的悬浮力进行了分析，计算范围为:

由于这两部分超出线性化模型的范围是关于原点对称的，本文详述了对第一部分的分析，用类似的方法即可求出另一部分的非线性模型。对第一部分利用有限元软件计算得到不同控制电流和偏移位置的悬浮力数据如表2所示，特性曲面如图7所示。

由图7可以看出悬浮力与控制电流和转子位置是非线性关系。利用多项式拟合软件1stopt，输入相对应的悬浮力、控制电流和转子偏移数据，通过快速公式拟合搜索命令，求出磁轴承悬浮力的近似非线性表达式可以表述为

表2 当－0.20 mm≤x≤－0.10 mm时，利用有限元计算所得的非线性部分悬浮力数据Table 2 The data of levitation force in nonlinear region by FEA element when －0.20 mm≤x≤ －0.10 mm

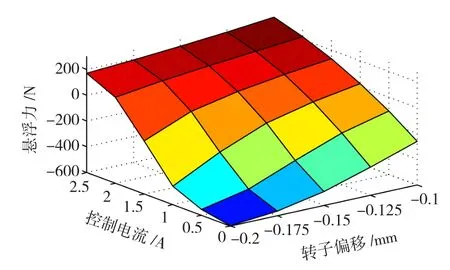
图7 当－0.20 mm≤x≤－0.10 mm时，悬浮力与偏移位置和控制电流的关系Fig.7 Relationship between levitation force，rotor displacement and control current when－0.20 mm≤x≤ －0.10 mm

对于第一部分，式(12)中系数可以确定如下:

用同样的方法可以求得第二部分的非线性表达式与式(12)相同，式中系数可以确定如下:

为了验证所得到的悬浮力计算公式的正确性，对于式(12)计算的悬浮力与由有限元计算所得的悬浮力进行了比较，如图8所示。可以看出，由拟合多项式计算的悬浮力与由有限元计算的悬浮力相差很小，这表明在磁轴承超出线性工作范围时，利用拟合多项式来计算磁轴承的悬浮力是可行的。

图8 非线性区由拟合公式(12)与有限元计算悬浮力的比较Fig.8 Comparison of calculated levitation forces using expression(12)with using FEA

5 磁轴承悬浮力模型的实验验证

为验证由磁场分析所得悬浮力计算模型的准确性，本文利用实验室的一台用于高速永磁电机的磁轴承系统，对于由计算模型所得的悬浮力进行了实验验证。

因实验条件所限，只对磁轴承线性化模型适用范围内的悬浮力进行了测试。首先通过调节PID参数使磁轴承处于稳定的静态悬浮，将径向轴承的X方向自由度调整到水平，确保在X方向的自由度不受转子重力的影响。然后调整传感器偏置找到电磁中心(在X方向的两线圈中的电流大小相等都是2.5 A)，测量转子在中心位置时控制电流与悬浮力的关系。在转子的一端施加X方向的外力，磁轴承控制系统将调节控制电流使转子处于电磁中心位置，此时由控制电流产生的电磁力等于所加载的外力。记录所施加外力转子处于电磁中心实现稳定悬浮所需要的控制电流。测试结果与计算所得悬浮力的对比如图9所示。

然后测量控制电流为零时转子偏移与电磁力的关系。改变位移参考电压，令转子偏离中心位置，调节PID参数，使转子稳定悬浮。在转子的一端施加X方向的外力，此时磁轴承控制系统会调节控制电流保证转子位于给定位置，直到控制电流为零，因此由偏置电流产生的电磁力等于所加载的外力。记录转子偏移位置和相应的电磁力。实验结果与计算所得的悬浮力对比如图10所示。

由图9和图10可以看出，与磁路法悬浮力计算模型相比，有限元法推导悬浮力公式计算值与实验结果更为接近。

图9 不同控制电流下悬浮力实验值与计算值的比较Fig.9 Comparison of tested levitation forces with calculated values for different control currents

图10 不同转子偏移位置悬浮力实验值与计算值比较Fig.10 Comparison of tested levitation forces with calculated values for different rotor displacements

6 结语

本文利用场路结合方法分析了径向磁轴承的悬浮力特性，推导了磁轴承悬浮力的线性化数学模型，确定了线性化模型的适用区域。对于线性化模型不能精确计算的区域，推导了磁轴承悬浮力的非线性数学模型。最后利用实验部分验证了所推导数学模型的有效性。研究表明，利用有限元法推导的悬浮力模型比磁路法模型更加准确有效。研究结果能够为磁轴承控制器的设计及验证提供参考。

［1］王凤翔.高速电机的设计特点及相关技术研究［J］.沈阳工业大学学报，2006，28(3):258 －263.WANG Fengxiang.Study on design feature and related technology of high speed electrical machines［J］.Journal of Shenyang University of Technology，2006，28(3):258 －263.

［2］SCHWEITZER G，TRAXLER A，BLEUDER H.Active Magnetic Bearings:Basis，Properties，and Applications of Active Magnetic Bearing［M］.Zurich:Vdf Hochschulverlag AG an der ETH Zurich，1994:4－8.

［3］曾励.永磁偏置的电磁轴承研究［R］.南京:南京航空航天大学，1999.

［4］OHJI T，MUKHOPADHYAY S C，LWAHARA M，et al.Permanent magnet bearings for horizontal-and vertical-shaft machines:A comparative study［J］.Journal of Applied Physics，1999，85(8):4648－4650.

［5］FUKATA S，YUTANI K.Characteristics of electromagnetic systems of magnetic bearings biased with permanent magnets［C］//5th International Symposium on Magnetic Bearings，August 5 －7，1998，Cambridge，USA.1998:234－243.

［6］诸德宏，洪益州，朱熀秋.基于α逆系统理论磁轴承数学模型及控制系统［J］.电机与控制学报，2009，13(4):496 －500.ZHU Dehong，HONG Yizhou，ZHU Huangqiu.Mathematical model and control of magnetic bearings based on α-th order inverse system theory［J］.Electric Machines and Control，2009，13(4):496－500.

［7］田录林，李言，田琦，等.大外径多环嵌套永磁轴承轴向磁力模型［J］.电机与控制学报，2009，13(3):349 －354.TIAN Lulin，LI Yan，TIAN Qi，et al.Planning and feasible region analysis of staticoperation points of conical magnetic bearings Axial magnetic force model for large outer diameter multi-annularnesting permanent magnetic bearings［J］.Electric Machines and Control，2009，13(3):349 －354.

［8］田录林，李言，王山石，等.双筒永磁向心轴承磁力工程化解析算法研究［J］.中国电机工程学报，2007，27(6):57 －61.TIAN Lulin，LI Yan，WANG Shanshi，et al.Research on magnetism engineering analytical calculation method for bi-barrel-shaped radial permanent magnetic bearings［J］.Proceedings of the CSEE，2007，27(6):57 －61.

［9］Christopher P F.Modeling and identification of active magnetic bearings and a toothless self-bearing servomotor［D］.Alberta:U-niversity of Alberta，2009.

［10］朱熀秋，邓智泉，袁寿其，等.永磁偏置径向－轴向磁悬浮轴承工作原理和参数设计［J］.中国电机工程学报，2002，22(9):54－58.ZHU Huangqiu，DENG Zhiquan，YUAN Shouqi，et al.The working principle and parameter design for permanent magnet biased radial-axial direction magnetic bearing［J］.Proceedings of the CSEE，2002，22(9):54－58.

［11］梅磊，邓智泉，赵旭升，等.基于磁通量计算的混合型轴向—径向磁悬浮轴承参数设计［J］.中国电机工程学报，2009，29(24):115－120.MEI Lei，DENG Zhiquan，ZHAO Xusheng，et al.Parameter design of hybrid axial-radial magnetic bearing based on magnetic flux calculation［J］.Proceedings of the CSEE，2009，29(24):115－120.