基于小波分形分析和脊波网络的模拟电路故障诊断方法

肖迎群 何怡刚

（湖南大学电气与信息工程学院 长沙 410082）

1 引言

模拟电路故障诊断自20世纪60年代以来构成了现代电路理论的热点研究领域和前沿研究领域，现已经发展成了网络理论中公认的第三大分支[1]。由此，业内的许多专家与学者已经提出了各种应用于模拟电路故障诊断的方法[1-8]。然而，由于模拟电路中元器件参数的分布性、广泛的非线性以及故障特征的复杂性，使得模拟电路故障诊断系统在其所构建系统的复杂性和故障诊断的正确性等方面还存在很多亟需解决的问题。为此，将神经网络和小波分析等方法应用于模拟故障诊断系统，以期有效地提高模拟电路故障诊断的效率和正确性。在文献[2]中，作者将被测电路的脉冲响应信号不加任何预处理就作为神经网络的输入，从而对于一个很小的被测电路就导致一个很大的神经网络结构。所以，文献[3-4]中，作者将被测电路的脉冲响应信号进行了小波分析、主元分析（PCA）和数据归一化的预处理，获得了最优特征模式作为神经网络的输入，这在一定程度上减少了神经网络输入端子数，且其故障诊断的正确率仅97%左右。而在文献[5]中，作者在基于文献[3-4]中提出的预处理方法的基础上，利用张量小波构成的小波网络对模拟电路进行诊断，使得故障诊断正确率有了更进一步的提高，达到99%左右，但是这却带来了小波网络的隐层小波元构造的复杂性。另外，文献[7]提出的基于遗传算法和神经网络的故障诊断系统需要同时采集多个测试点的数据而使得样本数据的获取非常的困难。在文献[8]中，作者是在频域内对故障响应信号进行分析处理以实现故障诊断，由于需要对响应信号实施频域变换，也导致了样本数据获取的困难和处理步骤的增多。

因此，本文针对上述文献中出现的问题和不足，构造了一种新型的基于脊波的脊波神经网络即脊波网络应用于模拟电路的故障诊断。脊波[9-10]是一种新的逼近多变量函数的有效工具，它相对于傅里叶变换和小波变换来说具有更好的逼近速率。从一定意义上说，脊波是一种带有方向信息的小波函数，具有更多的维数信息，能处理更高维的数据，对直线性和曲线性状的奇异性具有很好的逼近效果，从而广泛地应用于多变量函数逼近和图像处理领域当中[11-14]。所以，利用脊波构成的脊波网络不仅克服了小波网络应对高维输入样本时需要大量的增加小波元节点的构成数目，增加网络的复杂度的不足，而且充分利用脊波函数的时频局部化特性以及利用方向信息处理线性和超平面奇异性现象的优势特点，以紧凑的结构和良好的泛化性能对模拟电路的故障模式实施有效而精确地诊断。同时，本文采用一种新型的小波分形分析方法对故障响应信号进行预处理，这种方法相对于通常采用小波能量计算法取得的故障特征模式来说，具有更好的精确性和更强的理论性，它是对故障响应信号进行小波分析的基础上获取其小波系数的分形维特征信息用作诊断网络的输入数据的。由于分形维特征对信号具有良好的表达特性，将其由PCA和数据归一化方法实施维数和特征提取后所获得的最优特征模式，不但具有最少维数的模式特征矢量，而且，当用作脊波网络的输入数据时能更精确地完成模拟电路的故障诊断。

2 小波分形分析

2.1 小波变换

小波作为一种新型的信号分析方法应用于信号与图像处理的广泛领域之中[15]。小波是将信号分解为能反映其本质信息的逼近部分和细节部分以便于进行进一步的分析和处理。小波变换是通过对一个母小波ψ(x)的伸缩和平移所构成的小波族实施相应的变换处理而实现的。小波族定义为

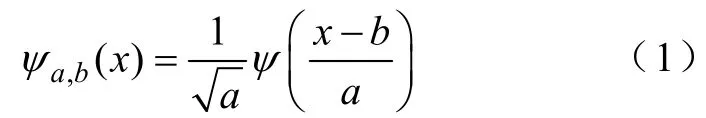
式中a，b—母小波的伸缩和平移参数。

给定一个信号f(x)和母小波ψ(x)，则信号f(x)的小波变换为

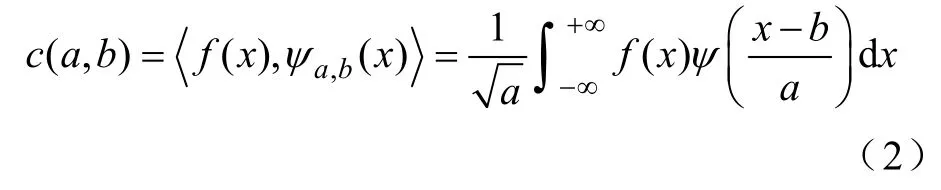
式中c(a,b)—信号f(x)的小波系数。

实际中，通常考虑信号f(x)的多分辨率分析。设{Vj}j∈Z是正交的多分辨率分析，{Wj}j∈Z是相应分解的小波空间，则f(x)在Vj上的正交投影表示为，即

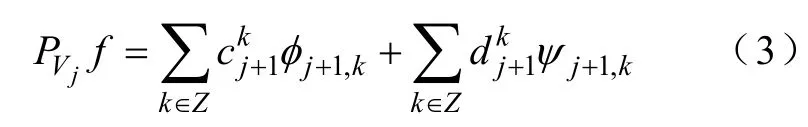
式中—f(x)在2j+1分辨率下的尺度系数；

—f(x)在2j+1分辨率下的小波系数。

由此可知，cj+1和dj+1分别为f(x)在2j+1分辨率下的逼近部分和细节部分即信号f(x)的低频分量和高频分量。相应地，{Vj}j∈Z可做出如下的空间分解

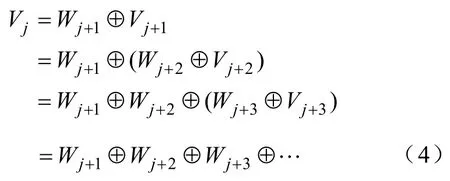
2.2 分形维

分形维数指一个几何物体的非整数维或分数维，是对自相似性图形的复杂性程度的一种度量[16-17]。在信号分析领域，信号波形或波形曲线可以看成是一种几何图形，所以分形维能对信号的复杂性进行有效的度量和实现相应特征的刻画，从而分形分析在生物医学信号处理领域得到广泛地应用[18-19]。本文使用Katz提出的信号波形的分形维数计算方法[17]来进行故障响应波形的计算以获取相应的故障特征模式。

Katz分形维数计算方法是在时域内直接对时变信号即波形曲线进行分形维数的估计计算。这种方法免去了Higuchi算法[18-19]中需构建二进制序列的预处理过程，从而具有简单直接、快速计算和节省存储空间的特点。

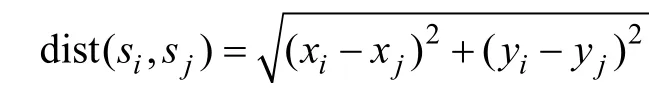
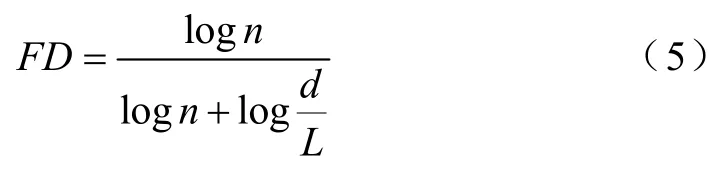
式中L—信号波形曲线的总长度即相继两点间距离的和；

d—序列的第一个点与序列中其他某个点的距离，而这个点就是相对于第一个点来说提供的距离为最大的那个，即d的数学表达式为

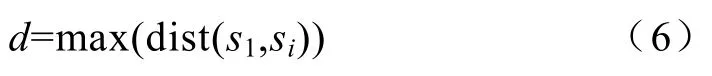
n—信号波形步长的数目，n=L/a；

a—相继两个点之间的平均距离。

根据2.1节所述的信号f(x)的小波分解方式，将信号f(x)在Vj空间的投影看作原始模式，在各子空间Vj+1,Vj+2,…,Wj+1,Wj+2,…上的投影看成小波分解的子模式，因此，本文就是对这些原始模式和小波子模式进行分形维数的计算从而获得相应的故障特征模式。

3 PCA和数据归一化

PCA[20]作为预处理的一种方式是对经过小波分形分析之后的故障数据实施进一步的维数降低和特征提取以获得最优的特征模式。具体来说，PCA就是将d维输入空间xd变换到另一个m维矢量空间zm，这里m＜d。因此，当对d维输入空间xd进行PCA处理时，首先将x写成d个正交归一化矢量ui的线性组合的形式

ui的子集和相应zi的值，从而得到x的逼近形式x˜为

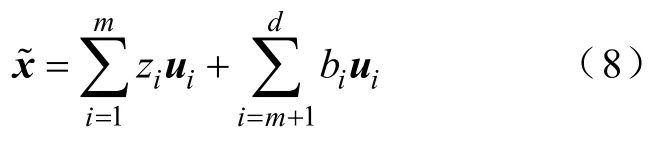
式中，剩余的i＞m+1个系数zi由bi取代。最后，定义一个对于N个样本数据的数据集具有平方和形式的Em为

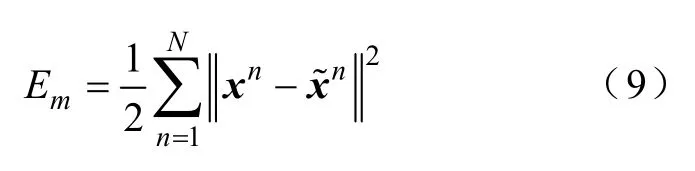
对Em进行最小化，从而得到元素为zi，i=1,…,m的矢量z即是在m维向量空间对原输入矢量x的逼近，即是相对于原输入矢量空间中x被提取的主元。

4 诊断电路及其特征提取

4.1 诊断电路与故障

本文考虑两个典型诊断电路的两类故障情形即Sallen-Key低通滤波器和四运放双二阶高通滤波器的单故障和双故障情形。使用小波分形分析和PCA来对这两个诊断电路进行信号预处理，从而获得电路故障响应的最优特征模式。为了比较方便，本文采用文献[3-4]中所给出的激励源，分别给两个滤波器施加幅值为5V，持续时间为10μs的脉冲波形，并在相应的电路输出端进行采样从而获得各自的故障时域响应信号。

4.1.1 诊断电路1—Sallen-Key低通滤波器

图1所示的即为中心频率为25kHz的Sallen-Key低通滤波器[3]，在滤波器电路中，电阻和电容的容差分别为5%和10%。给电路施加脉冲激励进行仿真时，如果电阻和电容在各自的容差范围内变化，则认为电路为无故障状态。

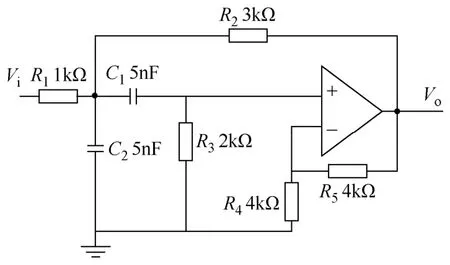
图1 Sallen-Key低通滤波器Fig.1 Sallen-Key low pass filter

单故障情形：当电路中的任何一个元件高于或低于它的正常值的50%而其他三个元件在它们的容差范围内进行变化时，对电路实行仿真从而获得所需要的故障冲激响应，然后再对这些故障响应信号进行相应地预处理最后得到9个故障类别即C1↑，C1↓，C2↑，C2↓，R2↑，R2↓，R3↑，R3↓故障和无故障类别（NF），这里↑和↓分别表示故障值高于和低于各自正常值的50%时所对应的故障状态。表1给出了Sallen-Key低通滤波器元件的正常值和故障值以及对应的故障类别。

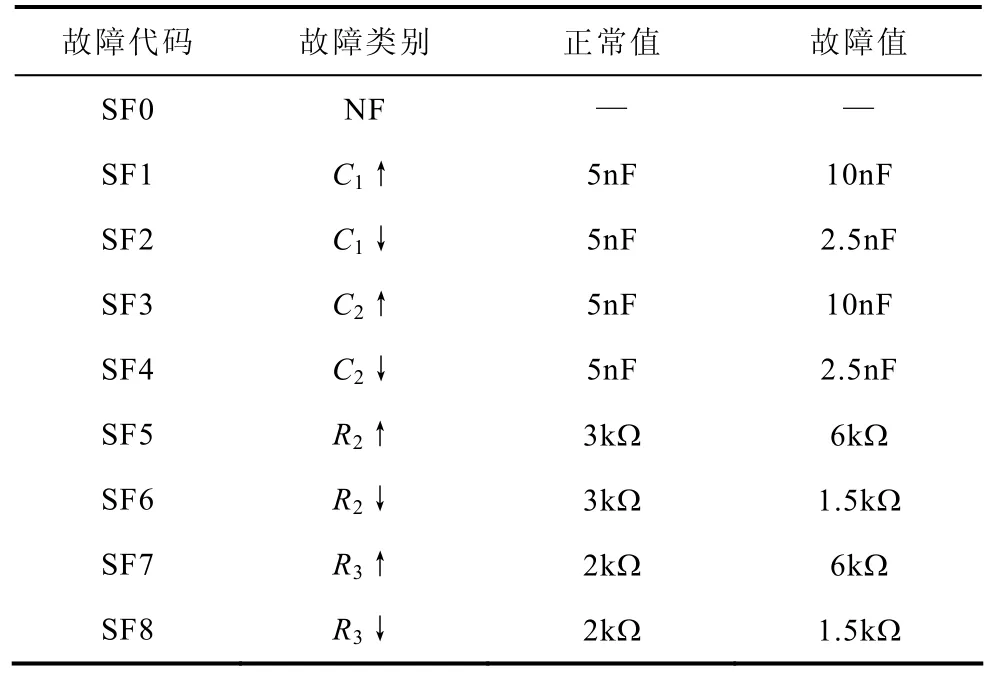
表1 Sallen-Key低通滤波器的元件正常值和故障值以及对应的单故障类别Tab.1 Single fault classes and the nominal and faulty component values used for Sallen-Key low pass filter

双故障情形：假设四个电路元件中的两个元件值同时高于或低于它们对应的正常值，而其他两个元件值却只在其容差范围内变化，从而得到相应的故障响应信号。这样，双故障类别的组合数即为=28，为了图形表示的方便性，这里只取其中一部分故障类别来加以说明，表2给出了这其中的7个故障类别。

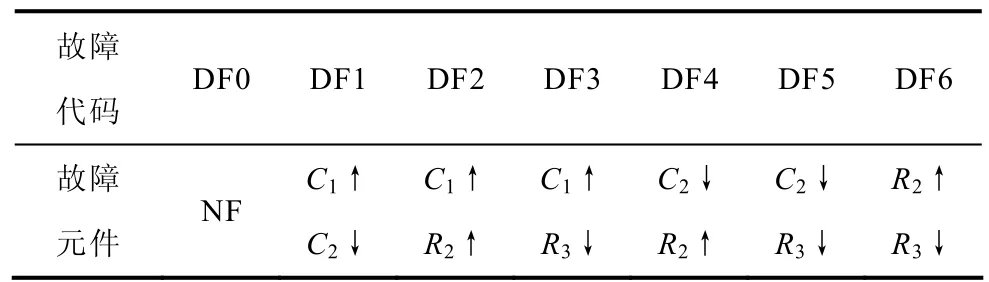
表2 Sallen-Key低通滤波器的双故障类别Tab.2 Double fault classes used for Sallen-Key bandpass filter

4.1.2 诊断电路2—四运放双二阶高通滤波器

图2所示的即为截止频率为10kHz的四运放双二阶高通滤波器[4]，其电路元件容差的设定同图1。

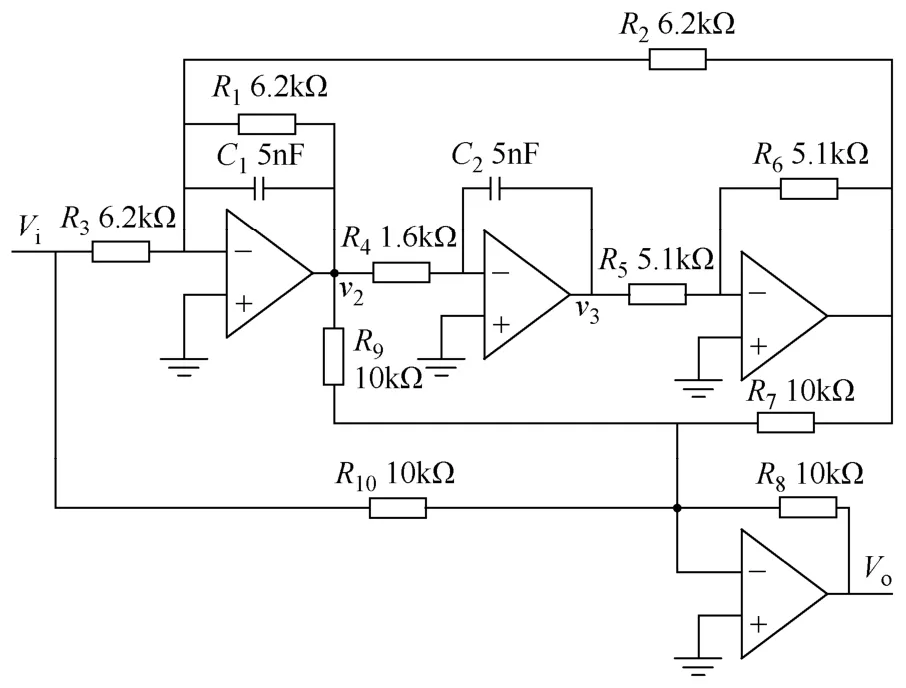
图2 四运放双二阶高通滤波器Fig.2 Four opamp biquad highpass filter

单故障情形：表3给出了电路的单故障类别以及电路元件的正常值和故障值设定情形。所以，得到13个故障类别包括C1↑，C1↓，C2↑，C2↓，R1↑，R1↓，R2↑，R2↓，R3↑，R3↓，R4↑，R4↓，和无故障状态（NF），其中↑和↓的表示情形同表1。

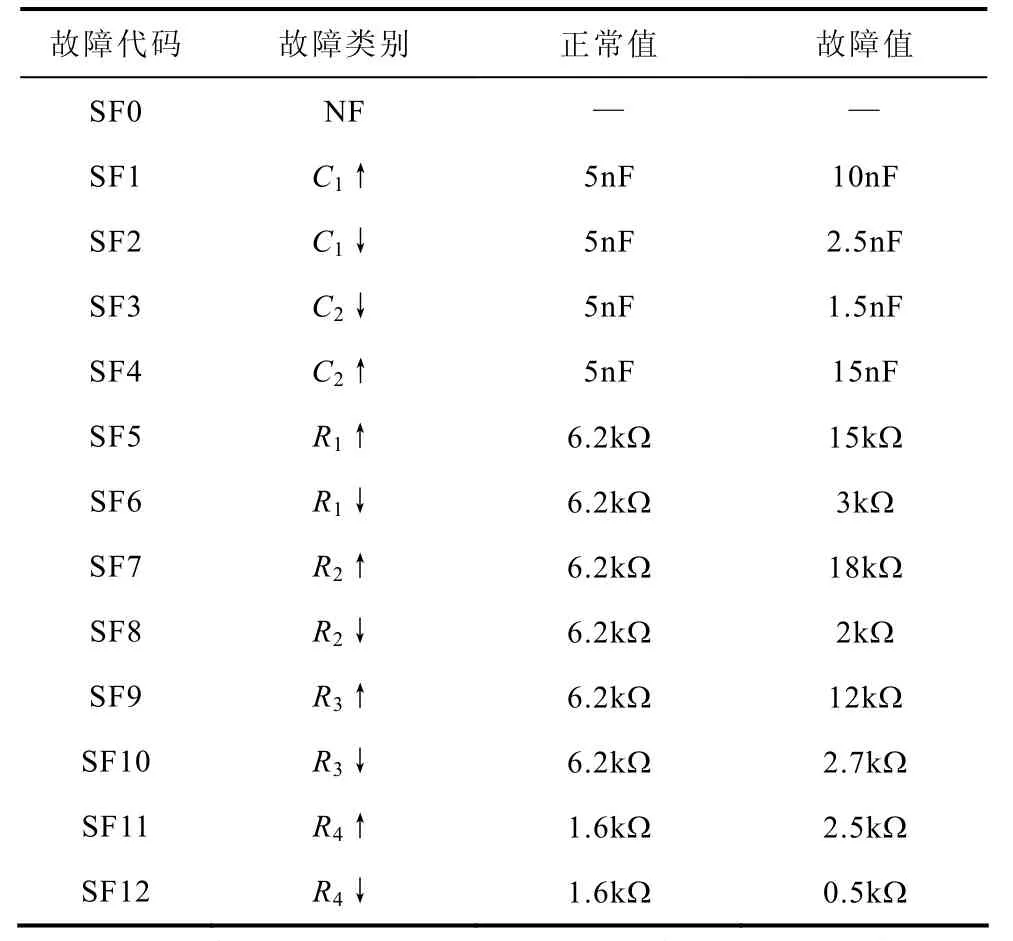
表3 四运放双二阶高通滤波器的元件正常值和故障值以及对应的单故障类别Tab.3 Single fault classes and the nominal and faulty component values used for four opamp biquad highpass filter

双故障情形：这里，假设6个电路元件中的2个元件值同时增加或减小，而其他4个电路元件值却只在它们的容差范围内变化，从而形成的故障类别数为=66，同样为了图形说明的方便性，只采用了其中一部分故障类别。表4给出了12个元件组合方式中的16个故障类别。

4.2 特征提取

这里，给两个滤波器电路分别施加幅值为5V，持续时间为10μs的脉冲波形，并采用以上所述的单故障和双故障情形时的元件故障设定值进行Spice的蒙特卡罗和参数分析，并在相应的诊断电路输出端获得对应于每个故障类别的60个故障响应信号。接着，再对这些故障响应信号进行3层Haar小波分解以获得相应的小波系数，同时对这些小波系数进行第2节所述的小波分形维数的计算从而得到每个故障响应信号的7个候选特征值。最后，对这些候选特征模式再进行PCA和归一化处理所得到的最优特征模式就作为脊波网络的样本数据以实行训练和测试。

图3给出了Sallen-Key低通滤波器中的元件C1发生C1↑故障时，对其中的一个故障响应信号f(x)进行3层Haar小波分形分析而产生的示意图。图3中，7个子图由上而下，从左至右分别对应于原模式信号f(x)和它的各层小波分解的子模式即第一层逼近系数cA1，第一层细节系数cD1，第二层逼近系数cA2，第二层细节系数cD2和第三层逼近系数cA3，第三层细节系数cD3。同时对这些模式信号进行分形维数的计算分别得到各自的分形维数为1.0041，1.1064，1.1394，1.0014，1.3792，1.0246和1.0178，再把这7个分形维数组合在一起就构成了所需要的一个候选特征矢量。最后，再对所有的故障响应信号经小波分形分析产生的候选特征矢量进行PCA和归一化处理就得到用于脊波网络实行训练和测试的样本数据集。在本文中，根据输入样本数据的相关矩阵R的特征值的特性来进行主元的选取，这些被选择出来的主元就是最终所需要的最优特征模式。因此，表5给出了输入样本数据的相关矩阵R的7个降序排列的归一化特征值，其中表中顶行的数字表示归一化特征值的个数，而SS，SD，FS和FD分别表示Sallen-Key低通滤波器的单故障情形，Sallen-Key低通滤波器的双故障情形，四运放双二阶高通滤波器的单故障情形和四运放双二阶高通滤波器的双故障情形。在这里，对小于等于0.001的归一化特征值进行截断处理，从而得到了用粗体和边框表示的被选中的主元特征值，它们均能说明各自占全体特征值99.99%的变化率。因此，根据表5中给出的结果，对SS，SD，FS和FD来说，确定它们各自被提取的主元个数为：2，2，3，3。同时，依据表5给出的被提取的主元个数，图4给出了两个滤波器电路在两种不同故障情形时的用各自主元数据即最优特征矢量表示的故障类别示意图。

表4 四运放双二阶高通滤波器的双故障类别Tab.4 Double fault classes used for four opamp biquad highpass filter

表5 两个滤波器在两种故障情形时对应于由PCA产生的输入数据的相关矩阵的降序排列的归一化特征值Tab.5 The normalized eigenvalues of correlation matrices of input data produced by PCA arranged in descending order in the two fault cases of two filters

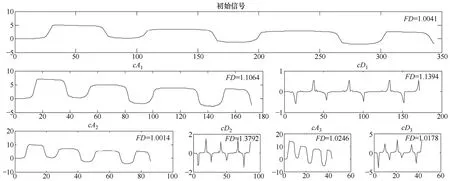
图3 三层Haar小波分形分析示意图Fig.3 Illustration of three-layer Harr wavelet-based fractal analysis

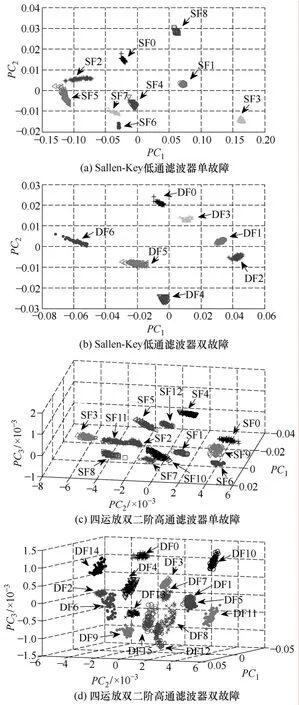
图4 两个滤波器在两种故障情形时用各自主元表示的故障类别Fig.4 The fault classes characterized by principal components in the two fault cases of two filters

5 脊波网络

5.1 脊波变换

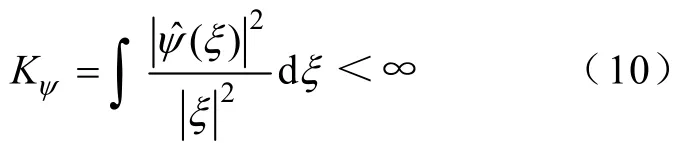
则称ψ为容许函数，而由ψ产生的脊函数ψγ就是脊波即ψγ=ψ((u·x-b)/a)，其中，参数γ=(a,u,b)中的三个变量：a表示脊波的尺度，u表示脊波的方向，b表示脊波的位置，它属于参数空间Γ，即Γ={γ=(a,u,b),a,b∈R,a＞0,u∈Sd-1,||u||=1}。参数空间Γ中的度量μ(dγ)定义为：μ(dγ)=σd/ad+1dadudb，其中σd是d维空间中的单位球Sd-1的表面积，du为球Sd-1上的一致概率度量。

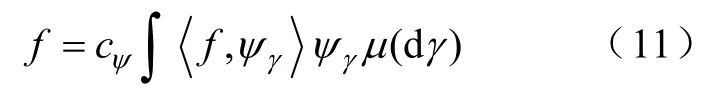
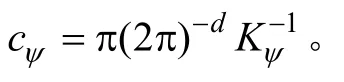
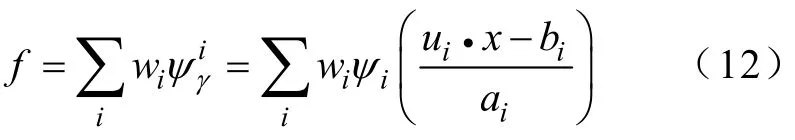
所以，式（12）可表示为：以脊波作为激活函数的多输入单输出单隐层前向脊波神经网络，这里wi为网络的输出层权值，它的值可通过网络的学习算法进行自适应调整来确定。

5.2 脊波网络体系结构

脊波网络的体系结构形式如图5所示。这是一个具有单隐层的三层（包括输入层，隐层和输出层）前向神经网络，它是将脊波函数应用于神经网络的隐层神经元作为激活函数构成脊波元而形成的脊波网络，图5中ψ(·)为脊波函数，φ(·)则根据具体应用的需要可选为Sigmoid类函数或线性函数。

将图5所示的脊波网络结构图写成数学表达式的形式为

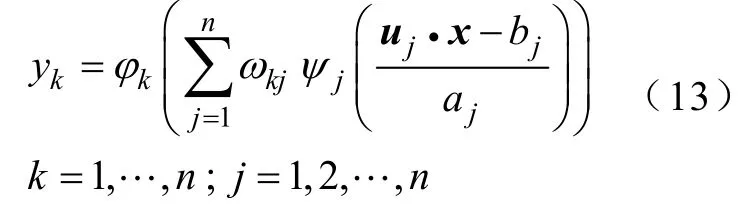
式中uj—第j个脊波元的方向矢量，

uj=(uj1,uj2,…,ujm) 且||uj||=1。

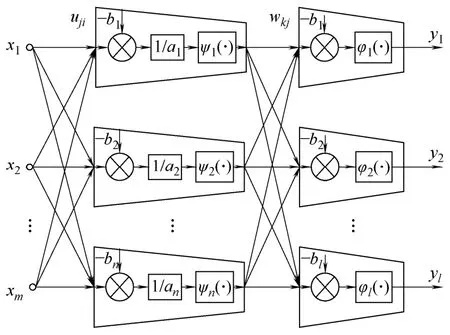
图5 脊波网络的体系结构Fig.5 The structure of ridgelet network

5.3 脊波网络结构设计

当前，研究人员已经提出了许多方法来对神经网络结构进行合理的设计，例如交叉验证法[20]、信息准则法[21-22]以及最小描述长度法[23]等等。但是这些方法一般都需要对估计函数的分布情形做出比较强的假设，或者需要进行多次试错尝试才能获得一个经验性的结果，这在一定程度上限制了这些方法的实际应用。

本文采用文献[24]提出的一种新型PCA方法来确定脊波网络的体系结构。它不需要对一些假定函数关系的参数实行估计而只需要简单的矩阵运算就能给出一个合理的结果，也即只需对将提取的主元进行一定准则的评估就能很容易确定脊波网络的体系结构。对一个特定的应用来说，脊波网络的输入节点和输出节点可根据输入和输出矢量的维数事先确定，所以这里主要就是使用PCA方法来选择脊波网络的隐层节点即脊波元的个数。其程序如下：

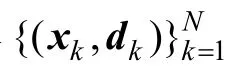
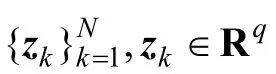
（4）最后对这组特征值进行一定准则的评估，从而取在全部特征值中占优势比重的特征值个数即为所需的隐层脊波元的个数q*。

因此，根据PCA方法确定脊波网络结构的程序，得到了由隐层脊波元的输出端数据构成的相关矩阵R的归一化特征值如图6所示。对Sallen-Key低通滤波器的单故障情形来说，依据图6得到其相关矩阵R的以降序形式排列的归一化特征值为：0.7460，0.4673，0.3487，0.2290，0.1552，0.1353，0.0868，0.0334，0.0067，0.0036，0.0019，0.0010，0.0005，0.0002，0.0002，0.0001，0.0001，0.0000，0.0000，…，0.0000。这里，统一确定将小于等于0.01的很小的归一化特征值进行截断处理，得到了占整个特征值的99.9%以上的变化率的前8个主元特征值就作为脊波网络对这种情形进行故障诊断时所使用的隐层脊波元的个数。依此类推，各获到了对应于Sallen-Key低通滤波器的单故障情形，Sallen-Key低通滤波器的双故障情形，四运放双二阶高通滤波器的单故障情形和四运放双二阶高通滤波器的双故障情形的脊波网络隐层脊波元个数分别为：8，7，16和16。

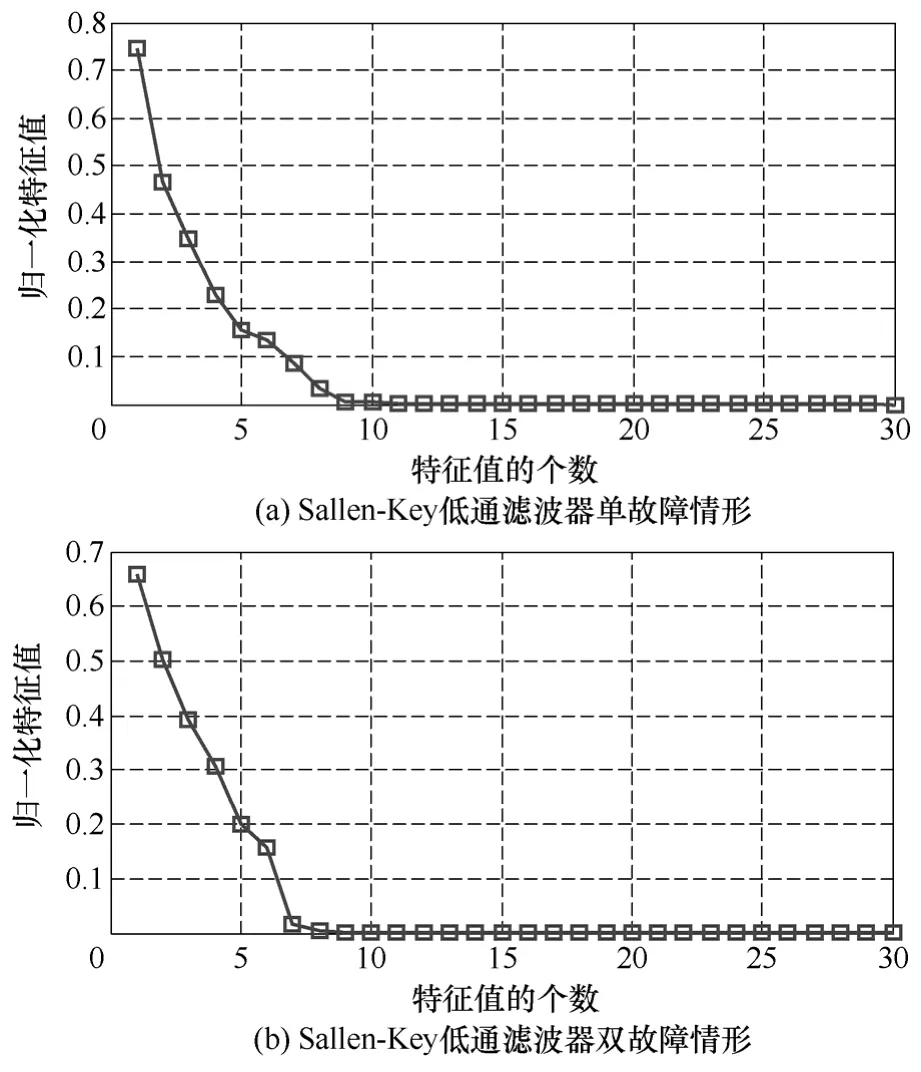
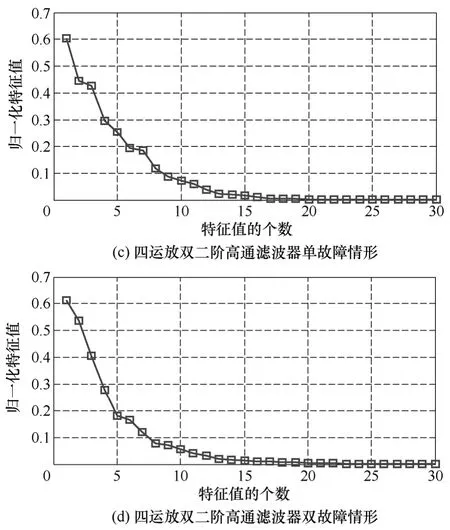
图6 两个滤波器在两种故障情形时对应于由PCA产生的隐脊波元输出数据的相关矩阵的归一化特征值Fig.6 The normalized eigenvalues of correlation matrices of the outputs of the hidden ridgelet units produced by PCA in the two fault cases of two filters

根据本节的分析，将采用一个三层的脊波网络的输出来估计每个输入数据属于不同故障类别的概率。脊波网络的输出值采用1对多即S选1的编码方法，这里假设脊波网络有S个输出神经元，如果某一输入数据属于某一故障类别p，则脊波网络的输出矢量t即为t(1)=0，…，t(p)=1，…，t(S)=0，这里S也表示待分类的故障类别的数目。因此，输入数据总是被分给由脊波网络的输出给出的具有最高概率的故障类。在本文中，脊波网络的隐层和输出层激活函数分别采用脊波函数和LOGSIG函数，训练方法采用文献[6]中所提出的最速梯度下降法和动量法相结合的方法来实施，这里统一选定学习速率为0.1，动量常数为0.2。注意，本文采用的脊波母函数是morlet小波函数[15]经适当的变换而得到的，它具有如下的形式

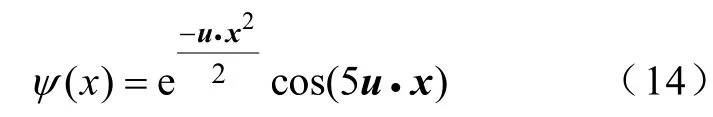
式中u—脊波的方向矢量；

“·”—内积。

6 仿真结果及其分析

根据以上各节提出的设计方法，对图1和图2所示的两个滤波器电路进行脊波网络的故障诊断，对应的训练集和测试集的大小则依据文献[4]的设置方法分别设定为每个故障类别20个和40个，即使用OrCAD10.5模拟仿真，首先生成每个故障元件即故障类别为60个的故障响应数据，然后将其导入Matlab，再在其中随机选取20个故障数据作为脊波网络的训练数据以实施对网络的训练，另外40个故障数据则作为它的测试数据以考察训练好的诊断网络的泛化性能及其故障元件诊断的正确性，接下来将通过具体例子进行详细阐述。

从图4中给出的故障类别分布图可以看出，Sallen-Key低通滤波器的单故障情形，Sallen-Key低通滤波器的双故障情形和四运放双二阶高通滤波器的单故障情形的故障类别之间都得到了很明显的区分即各种不同情形的故障类别都获得了很好的聚类结果，从而它们的故障辨识率都达到100%。同时根据上节给出的脊波网络结构确定结果，它们对应的脊波网络结构即输入节点个数，隐层脊波元个数和输出层节点个数分别为：Sallen-Key低通滤波器的单故障情形取为2，8和9，Sallen-Key低通滤波器的双故障情形取为2，7和7，四运放双极高通滤波器的单故障情形取为3，16和13。它们对测试数据进行分类所获得的故障诊断正确率均为100%。而对四运放双二阶高通滤波器的双故障情形的故障类别来说，发现DF1和DF5之间存在着少数几个故障类别的相互重叠，因此，与这种情形相对应的具有3个输入节点，16个隐层脊波元节点和13个输出节点的脊波网络进行故障诊断时，只存在着几个测试样本数据出现了错误的分类，诊断正确率达到99.9%左右。

表6给出了四运放双二阶高通滤波器对应于表4的16个双故障类别的诊断结果。表6中的每行对应于具有40个测试数据的一个故障类别，列则指对应于不同故障类别的40个测试数据被诊断的次数。例如，第二行表示属于DF0故障类别的40个测试数据全部被正确分类，而第三行则表示属于DF1故障类别的38个测试数据被正确分类，另有2个测试数据被错误分到了DF5故障类别中去了。从表6中可以看出，第7行中，存在着属于DF5故障类别的6个测试数据被错误分到DF1当中去了，它的34个测试数据得到了正确分类。因此，整个表中只有DF1和DF5类别之间存在着测试数据被错分情况，其他的故障类别都得到完全正确的分类，总的正确分类率达99.9%以上。这与图4给出的故障类别图形表示情形是一致的。

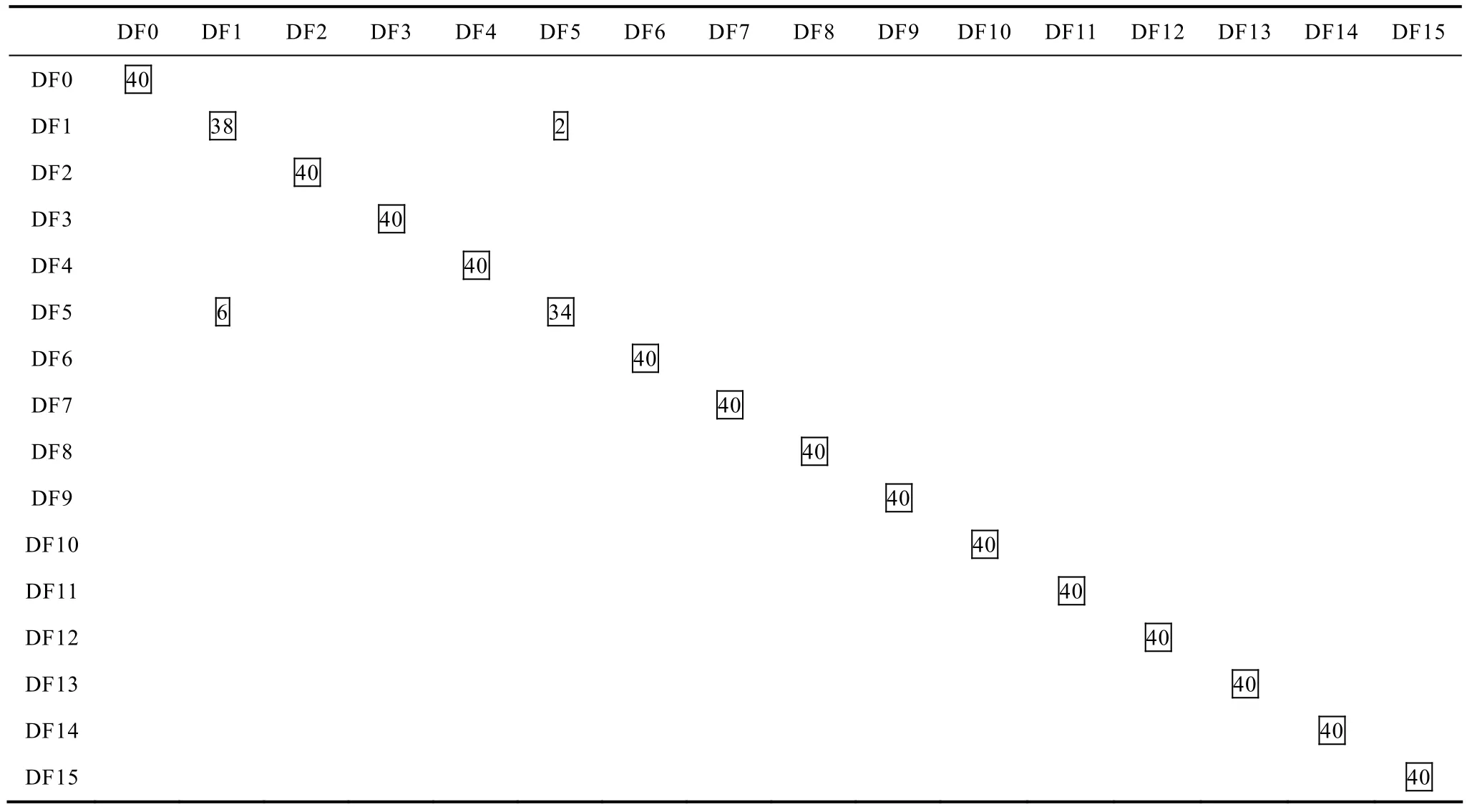
表6 四运放双二阶高通滤波器对应于表4的16个双故障类别的诊断结果Tab.6 Diagnostic result of the four opamp biquad highpass filter in diagnosing the 16 double fault classes corresponding to Table 4

将本文的脊波网络与文献[4]，文献[5]和文献[8]中的神经网络进行结构和性能的比较。

在文献[4]中，对Sallen-Key低通滤波器来说，神经网络的结构即输入节点数、隐层节点数和输出节点数依次为4，6和9，故障诊断正确率为97%，而本文的脊波网络结构为2，8和9，故障诊断正确率能达100%。对四运放双二阶高通滤波器来说，文献[4]的神经网络结构为5，16和 13，故障诊断正确率为95%，而本文的脊波网络结构为3，16和13，故障诊断正确率达100%。由此可见，本文提出的脊波网络在性能和结构上好于文献[4]中提出的神经网络诊断系统。

另外，在文献[5]中，小波网络结构为5，38和13，故障诊断正确率为99.95%。而本文的脊波网络则只需要16个隐层节点，并获得了相近的故障诊断正确率。

最后，在文献[8]中，对Sallen-Key低通滤波器能达到100%诊断率，对四运放双二阶高通滤波器却只实现99%的诊断正确率，而本文提出的脊波网络对两个滤波器电路均能实现100%的正确分类率。在结构方面，由于脊波理论的特定分析性质，本文的脊波网络在隐层节点的数量上稍多于文献[8]中神经网络。另外，文献[8]中提出的数据预处理方法是在频域内实现的，这增加了时域和频域数据转换的处理步骤，而本文的数据预处理方法是在时域内直接实现的，且能够根据故障类别之间的重叠程度灵活地选取主元的多少即最优特征向量的构成形式以实现最好的诊断。同时，本文提出的脊波网络结构选择设计方法同文献[8]中的根据经验公式来设计相比，是更具有理论依据性和灵活性，它能依据待分类数据的复杂特性灵活地选择隐层脊波元的数目，从而确定一个合理的脊波网络结构。

7 结论

本文研究结果表明，本文提出的脊波网络故障诊断系统能有效地实施模拟电路的故障诊断，对两种滤波器电路均实现几乎100%故障诊断正确率，并与以前的一些文献中提出的研究方法做了比较分析，突出了本文所采取方法的优越性，得出了令人满意的结果。同时，采用PCA方法来进行脊波网络的结构设计，使得隐层脊波元数目的确定更具有理论性、简单性、灵活性和可靠性。最后，脊波网络故障诊断系统不但能有效地诊断线性电路和非线性电路，而且能够诊断电路中的单故障和双故障甚至多故障现象。

[1] Bandler J W,Salama A E.Fault diagnostic of analog circuits[J].Proceedings of the.IEEE,1985,73(8):1279-1325.

[2] Spina R,Upadhyaya S.Linear circuit fault diagnosis using neuromorphic analyzers[J].IEEE Transactions.on Circuits and Systems II,1997,44(3): 188-196.

[3] Aminian M,Aminian F.Neural-network based analog-circuit fault diagnosis using wavelet transform as preprocessor[J].IEEE Transactions on Circuits and Systems II,2000,47(2): 151-156.

[4] Aminian F,Aminian M,Collins H W.Analog fault diagnosis of actual circuits using neural networks[J].IEEE Transactions.on Instrument Measurement,2002,51(3): 544-550.

[5] He Y,Tan Y,Sun Y.Wavelet neural network approach for fault diagnosis of analog circuits[J].IEE Proceedings-Circuits,Devices,System,2004,151(4):379-384.

[6] 肖迎群,何怡刚.基于脊波网络的模拟电路故障诊断[J].电工技术学报,2010,25(6): 155-162.Xiao Yingqun,He Yigang.A fault diagnosis method of analog circuit based on ridgelet network[J].Transactions of China Electrotechnical Society,2010,25(6): 155-162.

[7] Tan Y,He Y,Cui C,et al.A novel method for analog fault diagnosis based on neural networks and genetic algorithms[J].IEEE Transactions.on Instrument.Measurement,2008,57(11): 2631-2639.

[8] Yuan Lifen,He Yigang,Huang Jiaoying,et al.A new neural-network-based fault diagnosis approach for analog circuits by using Kurtosis and entropy as a preprocessor[J].IEEE Transactions.on Instrument Measurement,2010,59(3): 586-595.

[9] Candes E.Ridgelets: theory and applications[D].California: Stanford University,1998.

[10] Cande’s E J,Donoho D L.Ridgelets: a key to higherdimensional intermittency[J].Philos.Trans.R.Soc.Lond.A.,1999,35(17): 2495-2509.

[11] Donoho D L.Orthonormal ridgelets and linear singularities[J].SIMA J.Math.Anal.,2000,31(5):1062-1099.

[12] Candes E J.Ridgelets and the representation of mutilated sobolev functions[J].SIAM.Math.Anal.,1999,33(2): 2495-2509.

[13] Yang S,Wang M,Jiao L.Ridgelet kernel regression[J].Neurocomputing,2007,70(16): 3046-3055.

[14] Do M N,Vetterli M.The finite ridgelet transform for image representation[J].IEEE Transactions.on Image Process,2003,12(1): 16-28.

[15] Strang G,Nguyen T.Wavelet and filter banks[M].Cambridge,MA: Wellesley-Cambridge Press,1996.

[16] Falconer J.Fractal geometry-mathematical foundations and applications[M].West Sussex: John Wiley and Sons,2003.

[17] Kartz M.Fractals and the analysis of waveforms[J].Comput.Biol.Med.,1988,18(3): 145-156.

[18] Rosana Esteller,George Vachtsevanos,Javier Echauz,et al.A comparison of waveform fractal dimension algorithms[J].IEEE Transactions on Circuitd and Systems-Ⅰ: Fundamental Theory and Applications,2001,48(2): 177-183.

[19] Raghavendra B S,Narayana Dutt D.A note on fractal dimensions of biomedical waveforms[J].Comput.Biol.Med.,2009,39(9): 1006-1012.

[20] Bishop C M.Neural networks for pattern recognition[M].New York: Oxford University Press,1995.

[21] Fogel D B.An information criterion for optimal neural network selection[J].IEEE Transactions.on Neural Networks,1991,2(5): 490-497.

[22] Murata N,Yoshizawa S,Shun Ichi Amari.Network information criterion-determine the number of hidden units for an artificial neural network model[J].IEEE Transactions.on Neural Networks,1994,5(6): 865-871.

[23] Peter D Grünwald.The minimum description length principle[M].Cambridge,MA: MIT Press,2007.

[24] Yong R Park,Thomas J Murray,Chung Chen.Predicting sun spots using a layered perceptron neural network[J].IEEE Transactions.on Neural Networks,1996,7(2): 501-505.