工程施工测量基准及其坐标系统的建立方法探讨

夏显文

（中交第三航务工程局有限公司，上海 200032）

0 引言

在GPS测量技术得到广泛应用之前，较小规模的工程施工平面坐标系统常常采用一点一方向为起算数据，以此建立简单的独立工程施工平面坐标系。

随着大规模工程项目的兴起和GPS在各类工程施工测量中的广泛应用，工程施工平面坐标系统的定义方法已改变。通常的做法是选择国家坐标系统或地方坐标系统加上投影面的高程改正，有时也直接将GPS的WGS84坐标系统直接转换到工程坐标系中。由此建立的工程施工平面坐标系统可以做到任何两点间的由坐标差计算的距离与地面实测的边长一致。

但是由于改变投影面高程这一方法目前还没有明确的统一定义，因此在实际工程中采用的具体计算方法也各不相同，如所谓的“椭球膨胀法”、“椭球平移法”或者直接根据改变的高程面高度计算一个尺度，加到所选择的国家坐标系统或地方坐标系统上。这些方法在理论上定义模糊，并使得所建立的工程施工坐标系的平面坐标、大地坐标和空间坐标三者之间的简单换算关系被破坏，对后续采用GPS方法进行测量和计算带来困难。

为了解决这个问题，本文引进了工程施工测量基准、区域椭球及其定位定向的概念，并将采用GPS测设的平面控制网转换到区域椭球面上。由此建立的工程施工平面坐标系统既符合工程施工实际需要，又能达到定义明确、理论严密、过程清晰的目的。

1 参考椭球及其定位定向概念

在阐述区域参考椭球的概念前，首先需要回顾国家大地测量中关于参考椭球及其定位定向的概念。

在大地测量学中，一般采用一个恰当的旋转椭球来代表地球的形状，同某一地区大地水准面最佳拟合的旋转椭球叫做参考椭球。采用旋转椭球作为参考椭球其理由一方面是因为两者在形体上非常接近，另一方面是因为旋转椭球面是一个形状规则、数学表达方式相对简单的数学面，在其上可以做严密的数学计算。

参考椭球需要确定具体的几何参数（长半径和扁率），并对其进行定位和定向，依此建立某个区域的测量大地基准。

对于国家大地基准对应的参考椭球的定位定向需要满足以下条件：

1）椭球中心和地心重合。

2）椭球短轴平行于地球自转轴。

3）大地起始子午面平行于天文起始子午面。

2 区域参考椭球与工程施工坐标系

在我国测绘实践中，“参考椭球”的概念一般用于国家大地基准。为避免混淆，可以将在较小区域（如某个工程施工区域）内建立的工程施工测量基准对应的参考椭球称为区域参考椭球。

考虑到区域参考椭球仅应用于较小的工程施工范围内，区域参考椭球的几何参数对建立施工坐标系统的影响在数值上非常不敏感，因此区域椭球的几何参数可以定义为与某个已知的参考椭球的几何参数相同，这样既可以在使用上带来某些方便，在计算上也完全满足精度要求。

区域参考椭球的定位定向的目标是，使区域参考椭球面与工程施工范围内的水准面（一般不是大地水准面）最佳拟合。

同样，可以将经过定位定向的区域参考椭球称为工程施工坐标系的区域测量基准，区域测量基准的具体表现方式是施工控制网。

3 区域参考椭球的定位定向

3.1 方法描述

区域参考椭球的定位定向所要求的是使区域参考椭球面与工程施工范围内的水准面达到最佳拟合，这一条件还可以表述为，通过区域参考椭球的定位定向，使得区域参考椭球面与施工区域内的某个指定的水准面达到最佳拟合。

区域参考椭球作为区域测量的大地基准，其定位定向的结果也是通过区域控制网来具体体现的。因此区域参考椭球的定位定向实际包含在区域控制网（工程施工控制网）的建立过程中。

如果工程施工控制网采用GPS测量方式建立，并且通过GPS测量，已经得到控制网点在某个坐标系中的坐标（如我国的1954年北京坐标系、1980西安坐标系、2000国家大地坐标系或者直接是WGS84坐标系），那么，建立工程施工控制网的方法是：

1）测定部分或者全部控制点的正常高。

2） 根据区域参考椭球面与工程施工区域指定的水准面最佳拟合这一条件，求解一组坐标转换参数。

3） 经过该坐标转换参数通过坐标转换得到工程施工坐标系。

这样把区域参考椭球的定位定向问题归结为坐标系统转换参数的求解。

3.2 数学模型

3.2.1 同一坐标系下的空间坐标与大地坐标的换算关系

在同一坐标系下的空间坐标为（X、Y、Z），大地坐标为（B、L、H），则有：

取其微分得到：

式中：M为卯酉圈的曲率半径。

式（2）另可表示为：

3.2.2 不同坐标系下的坐标转换关系

两个不同坐标系下同一点坐标的空间坐标分别为（X1、Y1、Z1）、（X2、Y2、Z2），大地坐标分别为（B1、L1、H1）、（B2、L2、H2），则有：

式中：ΔX0、ΔY0、ΔZ0为平移量；εX、εY、εZ为旋转量；m为尺度系数。

当两个椭球的几何参数相同，且尺度系数m为0时，式（6）结合式（3）可以表示为：

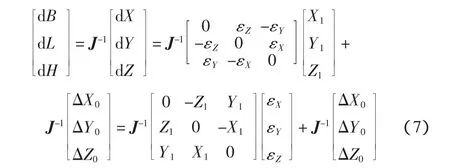
将式（7）结合式（1）、（3），得到：

3.3 参数解算

前面在表述工程施工坐标系的定义时，仅要求达到高程的最佳拟合。但在式（8）中看到，坐标转换的结果大地坐标也会产生变化。因此，在实际计算参数时可以增加对d B、d L的限制条件。

若GPS控制网点高程转换前为H1，转换后为H2，该点的正常高为h，H0为指定的工程施工坐标系的基准面的水准面高程。则：

式（9）表明，若在工程施工坐标系中控制点的正常高h等于H0时，该点的大地高H2为0。

给定计算坐标转换参数的条件可以定义为：

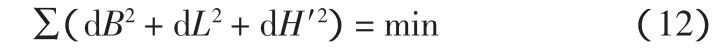
式（12）中求和的范围是控制网中所有参与计算的高程点（下同）。

为表述方便，引入以下符号：

这里引用的标记B、X与公式中其他部分字母相同但含义不同，不能混淆。m为所有参与计算的高程点总数。

这样式（12）的限制条件可以表述为：

根据式（13）的条件，可以最终得到：

作为特例，当控制网中仅有1个高程点时，可以忽略旋转参数（εX、εY、εZ），并令d L=d B=0，由式（8）得到：

4 结论

在建立工程施工坐标系统中，采用坐标转换概念确定工程施工测量基准及区域椭球定位定向参数，使得在建立工程施工坐标系的过程和方式上达到数学上的严密和统一，可避免由于采用不同方法引起的混乱和结果上的不确定性。

[1] 陈永龄.大地测量学[M].北京：测绘出版社，1957.

[2] 熊介.椭球大地测量学[M].北京：解放军出版社，1998.

[3] 朱华统.大地坐标系的建立[M].北京：测绘出版社1996.

[4] 陈健，晁定波.椭球大地测量学[M].北京：测绘出版社，1989.

[5] 刘大杰，陶本藻.实用测量数据处理方法[M].北京：测绘出版社，1998.