负孔隙水压力和毛细张力的关系及其对时效稳定的贡献

程玉梅

（中国石油大学储运与建筑工程学院，山东 青岛 266555）

0 引言

地下水位大幅度上升或下降，有效自重应力相应增加或减少，孔隙水压力变化；地下水位相对静止，也还是有孔隙水压力变化的，这是渗透作用所致，孔压大小由毛细水上升的高度确定。

渗透能产生毛细水压力，原状土从地下某深度处取出将产生负孔隙水压力，则是卸荷形成毛细水压力所致；成桩钻孔，地下连续墙成槽，基坑开挖等卸荷问题都会产生负孔隙水压力，而负孔隙水压力则与毛细水压力直接相关。

本文从毛细水压力入手分析毛细水上升高度、表面张力与渗透系数、黏滞系数、孔隙率等参数的相关性，同时分析了毛细张力对稳定发挥的积极作用。

1 表面张力与负孔隙水压力的关系

如图1所示，地下水向上渗透，水分布到土粒内部相互贯通的孔隙里，形成许多形状不一、直径互异、彼此连通的毛细管，取一根毛细水柱为分析对象：

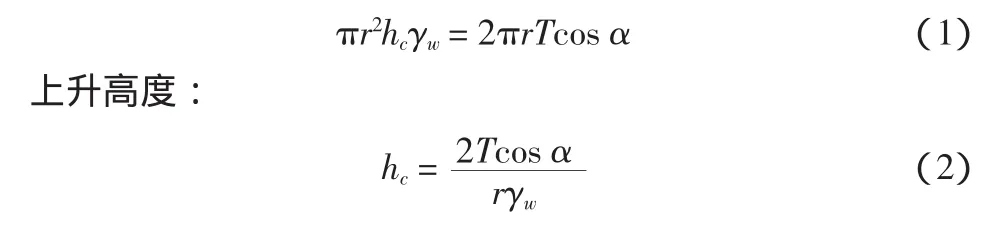
式中：hc为毛细管水上升高度，cm；T为表面张力；α为浸润角（对于大多数土α=0）；r为毛细管的半径，cm。

式中：S为单位体积的内部表面积或毛细管表面积，cm2；n为单位体积的孔隙体积，即孔隙率。

孔隙水压力：

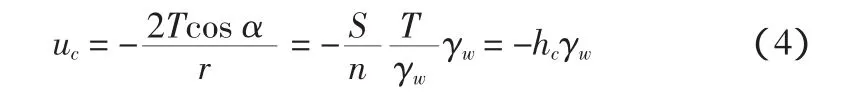
该孔隙水压力由渗透所致，应该和渗透系数k相关。

分析其中的一根毛细管（见图2），半径为r，截面积为a，截面上流速v（r1）呈抛物线分布。在L长度上有水头损失h，即水力坡降i=h/L，渗透力：

则半径为r1的管流水体所受总渗透力：

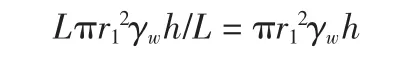
该力被周边的水体的阻力所平衡，阻力2πr1Lτ，其中τ为水的黏滞力，对牛顿黏滞流体：

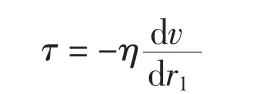
式中：η为液体黏滞系数。令阻力等于总渗透力：

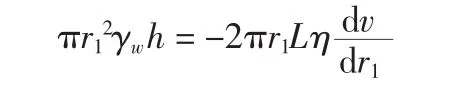
可得-2ηd v= γwir1d r1

运用边界条件r1=r，v=0，积分得半径r处的流速v=

将r1从0积分到r，可得：q0=如单位截面积有m根毛细管，则ma=n（n为孔隙率），单位截面积的流量q=mq0，从而得到q

由达西定律知：单位面积渗流量q=vt=kit

表1就是Winterkorn按公式（5）的计算结果和试验值的对比。除个别太离散外，试验值大致是计算值2倍的关系。而土的渗透系数可以依据土工试验规则给定的方法及黏滞系数η测定出，然后乘折减系数得出计算值。这样就能依据公式（5）确定S，孔隙率n由土的基本物理指标确定，由于孔隙水压力uc可以量测，则孔隙高度hc由式（4）可得，将S、uc、hc代入公式（3）就可以得到表面张力T了，这对于卸荷的基坑等工程的坑壁的时效稳定分析是很有帮助的。此表面张力与主动土压力强度进行比较就可以预估其对坑壁的稳定性贡献，这是定性的分析。

表1 毛细管水上升高度和渗透系数的关系

表面张力是负孔隙水压力产生的直接原因，孔隙水压力则可以量出或通过斯凯普顿公式进行定量的分析，也就定量地分析了毛细张力对卸荷坑壁、孔壁稳定的贡献。

2 稳定性安全系数的定义

由以上关于自重应力分析知：毛细水的存在不得不引起人们的注意。其实关于毛细水形成负孔隙水压力的分析还有其更为有价值的地方。由极限平衡理论知：在土体破坏之前，剪切角 θ＜φ′（或 sin θ＜sin φ′，见图 3）。θ与 φ′之间的差值越大，土体的安全储备越大，因此可以F=来判断土体的稳定性。

2.1 基本理论

在半无限空间土体中，钻一个半径为a的长圆柱孔，如图4。钻孔以后，柱孔周围应力分布可根据弹性理论解求得。

若初始应力场取K0=1.0，则：

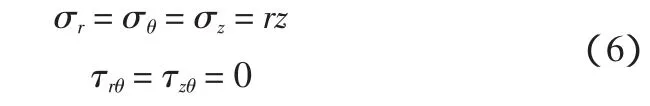
土体卸荷，柱孔周围的附加应力：

各式中：Δσr，Δσθ，Δσz分别为径向、环向及竖向应力变化值；a为圆柱孔半径；ρ为柱孔中心至计算点的距离；z为深度；γ为土的重度。

根据公式（7），计及孔内泥浆重度γs（假定无泥浆超高）时的附加应力为：

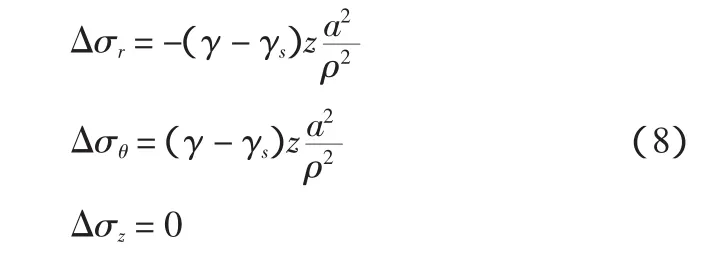
根据式（6）、（8），得孔周土体的有效应力：

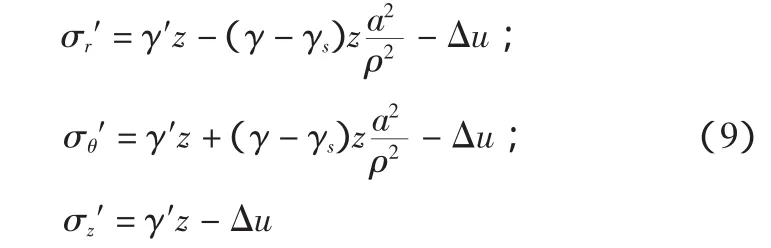
式中：γ′为土的有效重度；γs为孔内泥浆重度；Δu为由卸荷而产生的超孔隙水压力。

2.2 孔周土体的平衡条件

2.2.1 c=0且不考虑毛细吸力的影响

对于空间应力状态有：

假设土在各个方向上抗剪强度相同，则在不同距离上的稳定安全系数为：

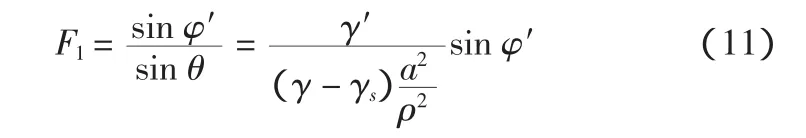
式中：F1称为基本稳定安全系数，是由土体本身的浮容重和内摩擦角而形成的；与相对距离成正比，距离孔中心越远越稳定；与泥浆重度成正比，泥浆重度越大越稳定。

2.2.2 考虑毛细吸力和黏聚力c影响

2.2.2.1 毛细吸力的计算

钻孔孔壁新鲜的表面上，由于毛细弯液面的作用形成一层所谓收缩膜，承受钻孔应力释放产生的毛细压力，增加孔壁的稳定性。实质上，毛细吸力就是卸荷而产生的负孔隙水压力。对空间应力状态，毛细吸力可以根据斯凯普顿公式计算：

式中：ΔσOCT为八面体正向应力增量；ΔτOCT为八面体剪应力增量；β，α分别为空间应力条件下的孔隙水压力参数。

由公式（8） 可得：

某工程第④层土中间12.45 m处，无侧限抗压强度qu=56.8 kPa，φ′=29°，c′=11 kPa。

因 σ1=qu，σ3=0，

根据有效应力原理 σ1′=qu-u，σ3′=-u，则由极限平衡理论得：

其中，负值代表毛细吸力，正值代表毛细压力。根据公式（9），可得考虑毛细吸力后孔周土体的有效应力：

F2称为时效稳定系数。它随着负孔隙水压力的消散而减小，是随时间而衰减的量（系数从0.625减至0），同时也是一个与深度有关的量，深度越大，土层原有的固结压力越大，试验所得到的无侧限抗压强度qu越大，则由式（14）算得的系数会大于0.625，土体越稳定。负孔隙水压力以收缩膜的形式而存在，因而土体的扰动对其影响很大。施工要赶进度，以充分利用收缩膜，减少投入。

2.2.2.2 考虑毛细吸力和黏聚力的稳定分析

毛细吸力和土黏聚力是两个十分重要的附加稳定因素。考虑毛细吸力和土黏聚力对孔壁稳定的有利影响，可将公式（10） 改写为：

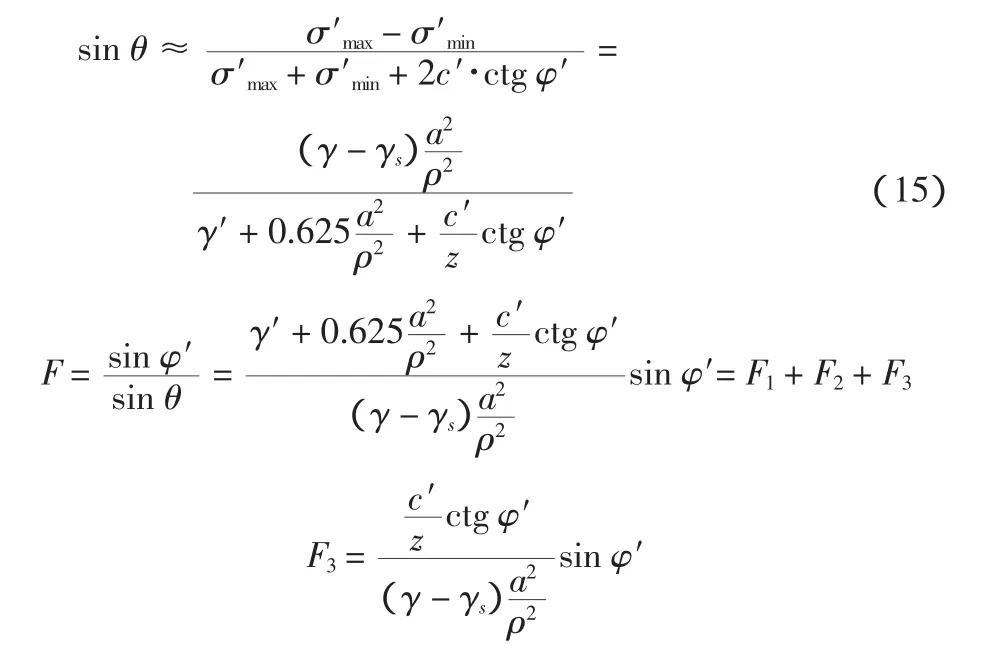
F3为反应黏聚力对稳定的有利影响部分。其影响程度随深度的增加而减小。

F称为总稳定系数，由基本稳定系数，时效稳定系数和黏聚力影响稳定系数三部分组成。下面就工程实例来分析各部分对稳定性的贡献。

3 工程实例

某工程第④层土φ=29°，饱和重度γ=18 kN/m3，有效重度 γ′=8 kN/m3，泥浆重度 γ =11 kN/m3，c′=11 kPa。第④层土中间12.45 m处，孔周土体在半径方向稳定安全系数F1、F2、F3、F如表2所示。

表2 孔周土体在半径方向稳定安全系数

从表2可以看出时效稳定系数F2在孔壁已达到了基本稳定系数的78%，这对孔壁土体的稳定具有重要意义，在2倍孔径外还占到20%左右，因而应充分利用这一有利的影响因素。

4 结论

1） 重力水产生正的孔隙水压力，毛细水产生负的孔隙水压力，由渗透系数可以初步确定毛细表面张力。

2） 钻孔孔壁总稳定系数由基本稳定系数，时效稳定系数和黏聚力影响稳定系数三部分组成。其中基本稳定安全系数是由土体本身的浮重度和内摩擦角而形成的，与相对距离成正比，距离孔中心越远越稳定；与泥浆重度成正比，泥浆重度越大越稳定；时效稳定系数，随着负孔隙水压力的消散而减小，是随时间而衰减的量；黏聚力影响稳定系数反应黏聚力对稳定的有利影响，其影响程度随深度的增加而减小。

3） 负孔隙水压力以收缩膜的形式存在，因而土体的扰动对其影响很大。施工要赶进度，以充分利用收缩膜，减少投入。

[1]胡中雄.土力学与环境土工学[M].上海：同济大学出版社，1997.

[2] 吴家龙.弹性力学[M].上海：同济大学出版社，1993.

[3]H F温特科恩.方晓阳.基础工程手册[M].北京：中国建筑工业出版社，1986.

[4] Lade P V，Duncan J M.Stress-Path Dependent Behaviour of Cohesionless Soil[C]//Proc.ASCE，Vol.102，No.GT1，1976.

[5]Harry ME.Ground Water and Seepage[M].New York：Mc Craw-Hill，1962.