8PSK信号在衰落信道下信噪比盲估计算法*
2011-06-06周新力宋斌斌龚岳州
田 伟 周新力 宋斌斌 龚岳州
(海军航空工程学院训练部1) 烟台 264001)(海军航空工程学院电子信息工程系2) 烟台 264001)
1 引言
信噪比是数据通信的一个重要指标,与误码率有直接的对应关系,可表征通信链路的性能与硬件电路设计的好坏,可为信道估计、数据解调、通信频率调整等提供重要参考依据。多年来在AWGN信道下PSK信号信噪比的估计方法已经产生了很多有意义的研究成果,这些研究算法主要分为两类:根据接收端是否有训练序列数据可用,可分为基于数据辅助(DA,Data Aided)和非数据辅助(NDA,Non Data Aided)的信噪比估计算法[1]。在基带数据模型下,以上两类算法均要求信道系数为实值,并根据有无训练序列情况,或要求信号调制方式、或在一帧数据范围内信道系数恒定等,才能取得较好的信噪比估计性能[2~7]。文献 [8]对BPSK调制信号在常见衰落信道下的信噪比估计进行了研究,该算法主要利用了衰落信道的统计特性,无需训练序列即可完成信道的信噪比估计,并将其应用于Turbo译码中,利用估计的信噪比信息进行Turbo均衡,以降低误码率,取得了良好的效果。以上介绍的几种信噪比估计算法中,除文献[3]介绍的算法为数据辅助信噪比估计算法外,其它为非数据辅助信噪比估计。在非数据辅助信噪比估计算法中,文献[2,7~8]在高斯白噪声信道下QPSK和QAM调制、衰落信道下BPSK调制时,取得了较好的估计效果,但由于计算信噪比的观测向量范数过大而导致信噪比解析式系数数值大、致使信噪比估计值易受观测量波动影响。本文针对8PSK调制信号在衰落信道下的信噪比估计方法进行研究,提出了对观测向量进行归一化处理算法,以减小其范数和信噪比估计解析式的系数值,降低观测量对信噪比估计值的影响。
2 信号模型
本文研究的信号模型,遵循美军标MILSTD-110B,信号调制方式为8PSK,码元速率为2400Baud[9]。假设接收信号经过系统均衡,且同步误差足够小,接收信号近似符合加性高斯白噪声条件,码间干扰可以忽略,则均衡输出的信号可以表示为:
y(n)=As(n)+N(n) (1)其中s(n)为8PSK调制的标准信号星座图,A为时变信道衰落系数,服从特定类型的分布;考虑到信号s(n)的实部和虚部具有正负值均匀分布的特性,为计算方便,取A为正值单边的概率分布,其对应的概率密度函数为:
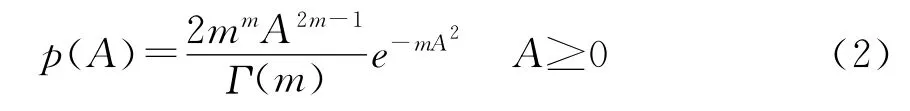
由A的分布特性可知,当m=0.5时,则信道衰落系数服从单边的、方差为1的高斯分布;m=1时,信道服从瑞利分布;当m趋于无穷大时,衰落信道蜕化为高斯白噪声信道。
N(n)为高斯白噪声,实部或虚部功率均为σ2,信道衰落系数A、信号s(n)和噪声彼此不相关。信噪比snr=E(|A|2)/2σ2。
3 信噪比计算
引入中间变量z:
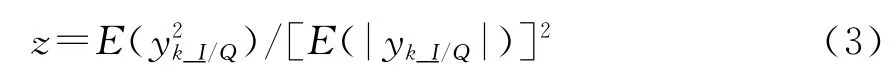
yk_I/Q表示接收的第k个码符号的实部或虚部。通过理论分析推导观测量z与信噪比的数值关系,并利用观测信号的时间平均,求解z值,从而解算信噪比。
3.1 复基带信号的分解
设8PSK信号在信号集中均匀分布,则实部与虚部的分布具有对称性,计算z时取实部或虚部的计算方式一致。现取其实部进行计算,实部取值及其对应的概率分布分别为:
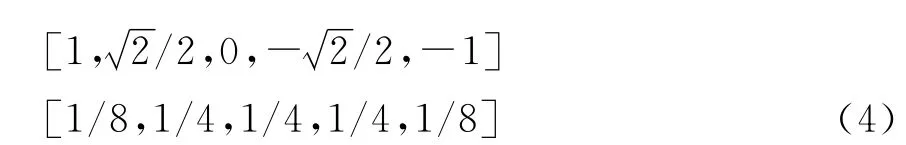
根据A与信号、噪声彼此间的不相关特性可得:
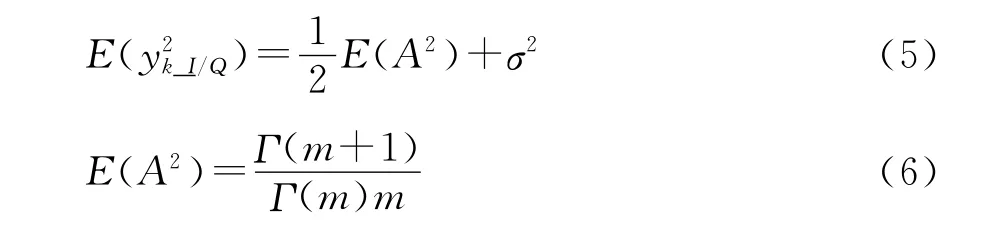
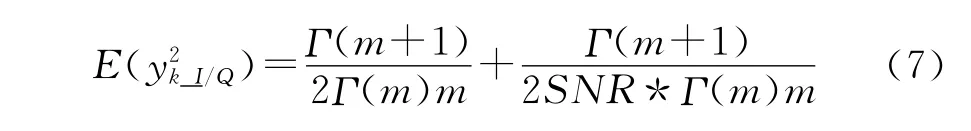
由高斯白噪声概率密度分布函数的对称性:
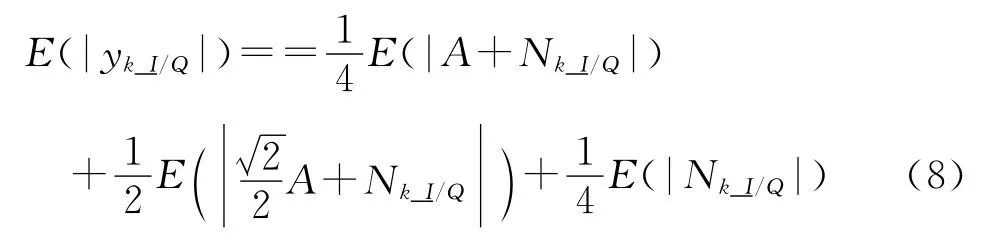
3.2 信噪比关系式解算
问题即可转化为计算E(|A+Nk_I/Q|)。利用条件概率特性,先视A为确定值,解算E(|A+Nk_I/Q||A)等式的条件期望,再对条件期望值中的随机变量A求期望。由高斯白噪声特性,可解算:
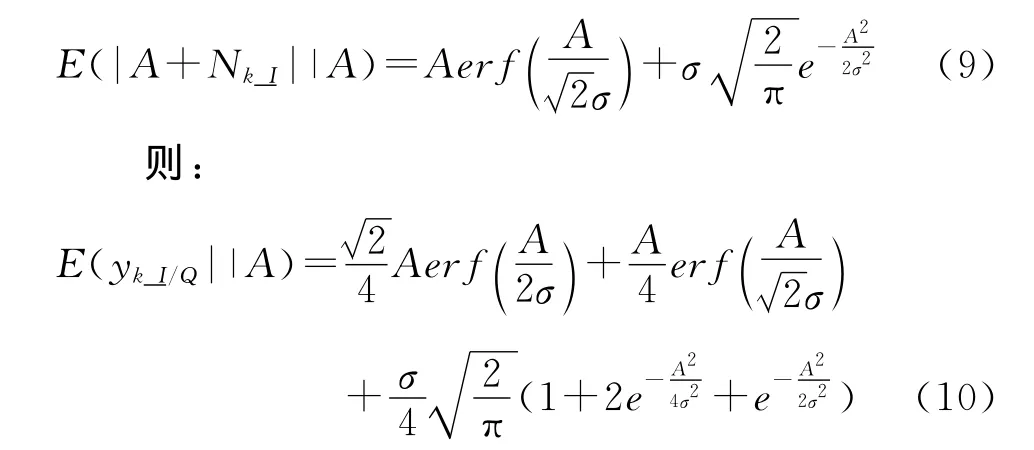
分别计算式(10)中各因子,根据文献[10~11],整理合并同类项可得:
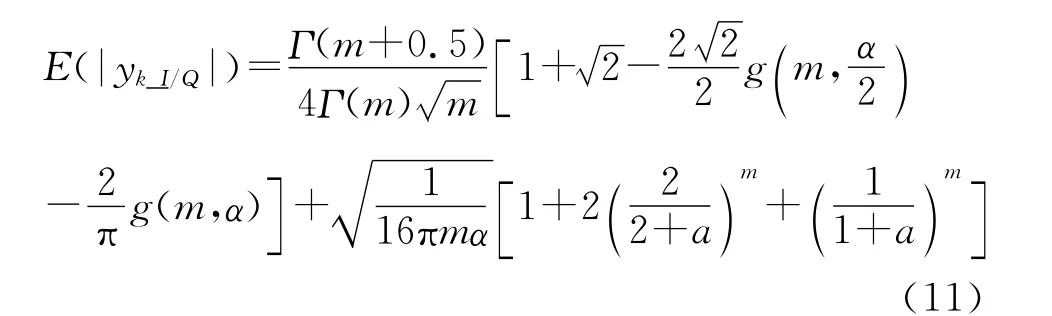
其中,
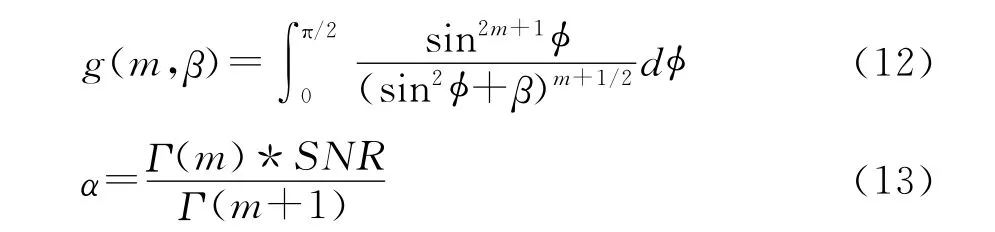
根据式(7)和式(11)得z与信噪比解析式:
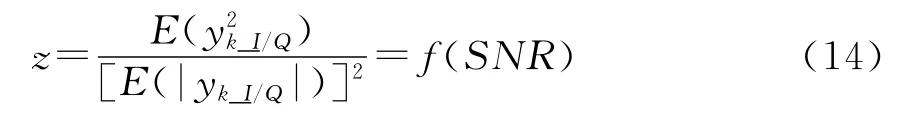
显然,单独利用实部或虚部求解的信噪比,与利用复信号求解信噪比相同。
3.3 信噪比关系式解算数据拟合
根据实际应用情况,可将信噪比范围限制在-10dB~10dB范围内,设信道系数分别服从高斯分布和瑞利分布,对应的m取值分别为0.5和1;考察-10dB~10dB范围内SNR与f(SNR)的关系,可知SNR与f(SNR)是单调函数关系,则可采用多项式数据拟合的方式,求解SNR=f-1(z)=g(z)。在数据拟合过程中发现,f(SNR)变化较小、观测量z构成的向量范数大,致使拟合多项式系数值非常大;z较小的变动可能会导致估计信噪比较大的偏移。故对z进行归一化处理,以分散z值的分布范围,降低拟合多项式系数值[13]。对每一个测试信噪比值求解的z值,作为一组向量Z,对其进行归一化处理(N为Z向量的长度,¯z为其均值):
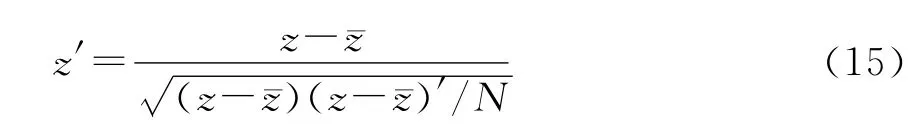
归一化f(SNR)与SNR关系如图1所示。

图1 归一化f(SNR)与信噪比的数值关系
由图1可以看出,归一化处理后,信道系数服从瑞利分布对应的中间观测量与信噪比曲线,在信噪比低于-4dB时,信噪比对中间观测向量的分辨率还比较低,易造成较大的信噪比估计偏差。因此,在进行曲线拟合时,对信道系数服从瑞利和高斯分布的情况,考察信噪比范围分别限制在-4dB~10dB和-10dB~10dB范围内。以下对6~9阶多项式拟合算法以0.1dB的步进值,进行仿真分析,多项式数值拟合关系、累积剩余误差如图2所示。
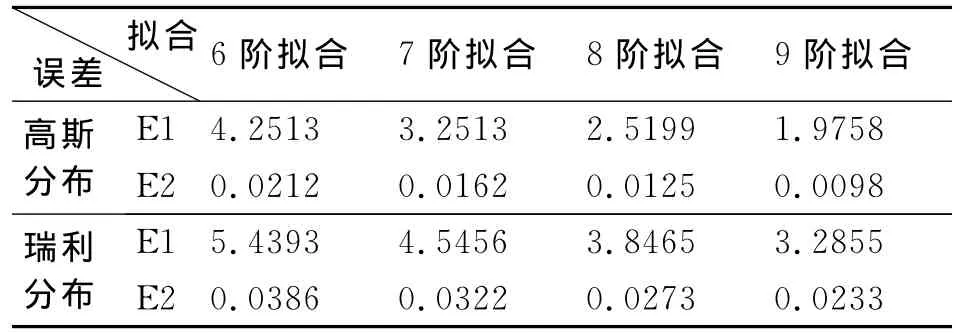
表1 归一化累计剩余误差与平均剩余误差对比
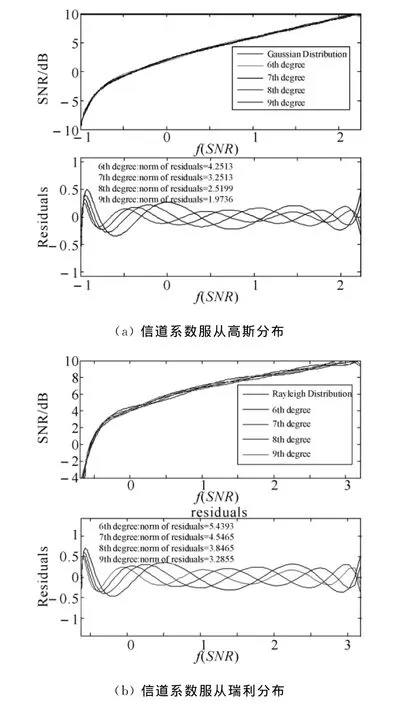
图2 不同阶数下数据拟合与累计剩余误差
不同阶数下多项式拟合的累计剩余误差与均方根误差对照表如表1所示。
经分析可知,拟合阶数越高,精度越高,相应的计算复杂度也越高;在计算复杂度与精度间折衷考虑,可采用9阶多项式进行曲线拟合。其多项式为:
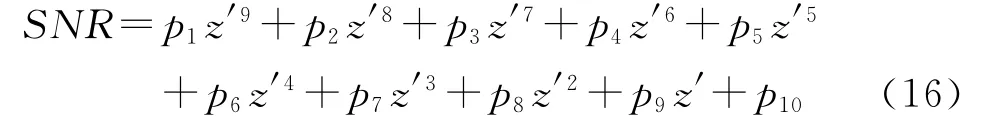
z′为归一化处理后z值。多项式(16)对应的系数如图3所示。
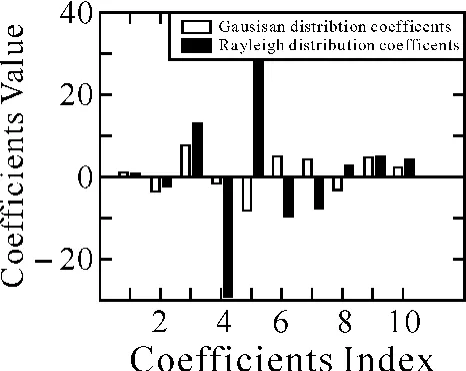
图3 归一化拟合多项式系数分布
由图3可看出,信噪比估计多项式(16)的系数值相对文献[2,8]中提出的信噪比估计算法,数值降低了3个数量级;而z′的变化范围相比z扩大近10倍,通过降低多项式系数和扩大z′值变化范围,可改善信噪比估计过程中,观测向量z的小范围变动引起估计信噪比值较大范围波动,提高信噪比估计的准确性。
在实际解算时,为充分利用接收信息,提高信噪比估计精度,取同相分量和正交分量联合估计,再对值进行归一化处理
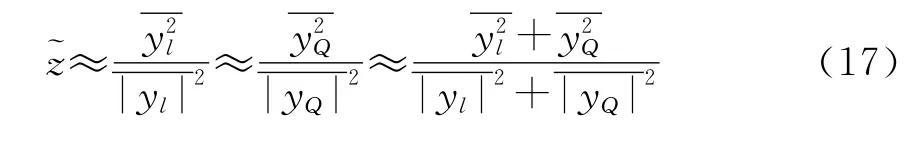
4 信噪比仿真
在信道系数服从高斯分布和瑞利分布情况下,取观察数据为2000和1000个码符号,分别利用接收信号实部、虚部和实部与虚部平均估计信噪比,进行100次蒙特卡罗仿真,估计信噪比与参考信噪比对比如图4、图5所示。

图4 2000个码符号的信噪比估计对照图

图5 1000个码符号的信噪比估计对照图
仿真结果表明,在0~8dB范围内,利用接收信号实部和虚部联合估计的信噪比精度非常高,2000个样本数据时,信道系数服从高斯分布和瑞利分布信噪比平均误差分别低于0.30dB和0.33dB;在0dB~8dB信噪比区间外,估计信噪比呈现极大值或极小值的单边偏离特性,估计误差大。改变接收数据长度,在采样样本数据为1000个码符号时,有效估计的信噪比范围进一步缩小,对信噪比的要求更高,这表明该算法对数据的统计特性要求高。另外,从仿真试验还可以看出,采用实部与虚部相结合的联合估计,比单独采用实部或虚部估计的效果要好;通过实部与虚部的统计平均,减小了中间观察向量的波动效应对信噪比估计的偏差影响。采用该算法估计信噪比的优点在于不需要训练序列为辅助数据,只需明确信道系数服从的分布特性,即可估计信噪比。其局限性在于它要求接收信号足够长才能提供对信噪比的精确估计;但较长接收信号,不利于信噪比信息的实时引用;如在窄带短波通信系统中,按照美军标MIL-STD-110B的标准,2000个码符号将至少跨越40帧的接收信息,不利于信噪比估计信息的实时应用。
5 结语
本文提出了一种信道衰落系数分布统计特性可用解析式描述的、归一化8PSK调制信号的信噪比盲估计算法;算法采用高阶多项式归一化拟合方式,通过将接收信号观测量作为影响信噪比的参数值求解信噪比,计算复杂度低、算法稳定。在信道衰落系数服从高斯分布和瑞利分布情况下进行的性能仿真表明,该算法在采样数据足够长的情况下,能适用在信噪比0dB~8dB范围内的信噪比估计,估计误差低于0.4dB,验证了该算法适用于衰落信道下8PSK调制信号信噪比估计的可行性。
[1]BEAULIEU N C,TOMS A S,PAULUZZID R.Comparison of four SNR estimations for QPSK modulations[J].IEEE Communication Letters,2002,4(2):43~45
[2]许华,樊龙飞,郑辉.一种精确的QPSK信号信噪比估计算法[J].通信学报,2004,25(2):55~60
[3]蒋政波,洪伟,刘进,等.基于数据辅助的AWGN信道下 QPSK信号信噪比估计[J].通信学报,2008,29(6):119~125
[4]REN G,CHANG Y L,ZHANG H.A new SNR's estimator for QPSK modulations in an AWGN channel[J].IEEE Trans on circuits and systems,2005,52(6):336~338
[5]SHIN J D,SUNG W J,KIM I K.Simple SNR estimation methods for QPSK modulated short bursts[C]//Proc IEEE GLOBECOM,2001:3644~3647
[6]Beaulieu,N.C.,Toms,A.S.,Pauluzzi,D.R.Comparison of four SNR estimators for QPSK modulations[J].IEEE Communications Letters,2002,4(2):43~45
[7]许华,樊龙飞,郑辉.QAM信号的非数据辅助信噪比估计方法[J].电子与信息学报,2005,275(2):202~205
[8]A.Ramesh,A.Chockalingam,L.B.Milstein.SNR estimation in generalized fading channels and its application to Turbo decoding[C]//International Conference on Comunications,2001(ICC2001)
[9]MIL-STD-188-110B.Interoperability and performance standards for data modems[S].US Dept of Defence,May 27,2000
[10]J.W.Caring.A New Simple and Exact Result for Cacaulating the Probability of Error for Two-Dimensional Signal Constellations[J].Proc.IEEE MILCOM'91,1991,10:571~575
[11]M.K.Simon,M.S.Alouini.Digital Communications over Generalized Fading Channels:A Unified Approch to Performance Analysis[M].Jihn-Wiley,2000
[12]胡海荣,覃亚丽,林文耀.基于分数阶傅里叶变换的LMS自适应滤波[J].计算机与数字工程,2009,37(2)
[13]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004,9:80~83
