大型泵站箱形进水流道内部流动数值模拟
2011-06-05周济人
周济人,金 燕,刘 超
(1.河海大学水利水电工程学院,江苏 南京 210098;2.扬州大学水利科学与工程学院,江苏 扬州 225009)
0 引 言
泵站进水流道是前池与水泵叶轮室之间过渡段,其作用是使水流由前池流向叶轮室的过程中能更好地转向和收缩,使水泵叶轮进口具有较好的流速分布和压力分布,进水流道内流态的优劣直接影响水泵的性能及安全运行[1]。某大型低扬程泵站为满足自引、自排、抽引及抽排要求,泵站进出水流道设计为箱形双向形式。目前对双向流道泵装置的研究多为模型试验[2-6],对其内部流场了解较少。本文采用CFD数值模拟方法[7-9]能够获取进水流道内的流场,可以详细了解流速分布情况,尤其是泵进口的流速分布,对改善进口水流条件,保证水泵性能的发挥和安全运行具有重要的意义。
1 计算模型
本文采用FLUENT软件对大型低扬程泵站双向箱形进水流道内部三维紊流流动进行数值模拟。
1.1 计算区域
数值模拟以进水流道为计算对象,前池和进水流道外形轮廓为计算边界,取整个进水流道包围的水体为计算区域,如图1所示。为了模拟水泵叶轮进口条件,进水流道出口设置了圆柱轮毂体。应用有限体积法离散和SIMPLE算法计算求解速度场和压力场。
1.2 控制方程
进水流道内水流运动作为一种收缩型管道运动,只要设计得当不易出现回流现象,因此采用标准k~ε紊流模型可满足计算精度要求。
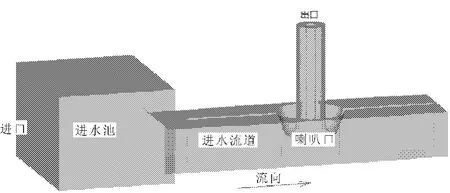
图1 计算区域
标准k~ε紊流模型是半经验公式[10],主要是基于紊动能和紊动能耗散率。其中k方程是精确方程,ε方程是由经验公式推导出的方程。
紊动能k方程
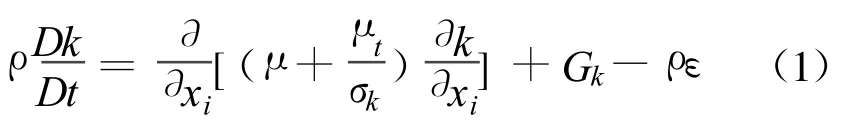
紊动能耗散率ε方程
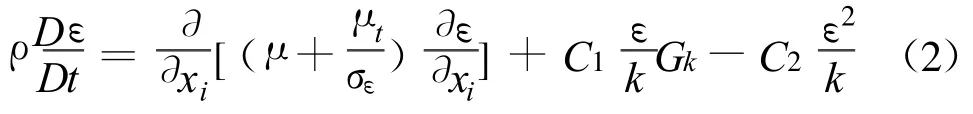
式中 :μt=为紊流粘性系数;Cμ为常数;Gk为由于速度梯度引起的应力生成项:

标准k~ε紊流模型方程中的常数通过经典实验得到,各相关常数如下:
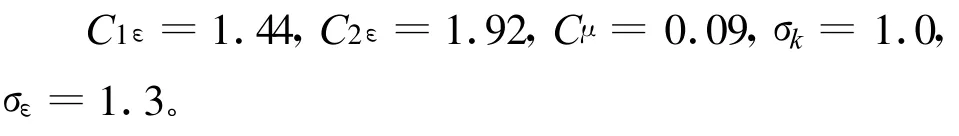
1.3 边界条件
1.3.1 进口边界
取在进水池上游较远处,认为来流已是充分发展的紊流,比较均匀。进水池入口的流速场给定,在水深方向设为对数式分布。
1.3.2 出口边界
取在泵吸水管出口处,认为出口流动已成单向状态,计算区域的解不受出口下游影响。
1.3.3 固壁边界
进水池中的固体壁面包括边墙、吸水管及其圆柱轮毂体等,采用标准壁面函数法,并在固体边壁处规定无滑移条件。
1.4 网格划分
进水流道采用非结构化四面体网格和六面体网格相结合的混合网格,以适应隔墩、喇叭口等不规则部件。
2 流场计算结果及分析
2.1 流场计算工况点的选取
通过数值模拟,可以得到进水流道内流场的速度、压力、流线等信息。为了便于分析、说明和比较,选取三个典型的工况点进行分析,分别是最优工况(Q=20 m3/s)、小流量工况(Q=15 m3/s)和大流量工况(Q=25 m3/s)。
以下各图中压强单位为Pa,流速单位为m/s。
2.2 粒子迹线图
图2为最优工况下整个流道的粒子迹线图,由图可知,水流由进水池进入喇叭口过程中直线段的流线均较为平顺,当进入喇叭口下方时流线急剧弯曲,由于进水流道的后部空间较大,水流的自由度大,在来流的带动下流道的后壁死水区流线紊乱,形成缓慢回流和漩涡,但该区流速较小。

图2 进水流道内的粒子迹线图
2.3 压力和流线分布
为了进一步研究进水流道内的流动情况,在最优工况下,截取了几个具有代表性的断面进行分析,分别是进水流道隔墩两侧的对称面(Z=-0.5 m,Z=0.5 m),靠近进水流道面层的断面(y=-0.5 m),靠近进水流道底层的断面(y=-2.7 m),具体位置见图3(a)和图4(a)。图3(b)、图3(c)、图4(b)、图4(c)显示的是不同断面上的速度等值线和压力云图。由图可知,从前池到进水流道,压力分布沿着水流的方向逐渐降低,流速逐渐增大,流态平顺。但在进水流道的后部是死水区,流速很小,且有明显的漩涡。从纵断面来看,进水流道内在隔墩的两侧断面上的压力分布和流速分布十分接近,说明水流基本上是对称的,死水区的漩涡靠近后壁;从水平断面来看,靠近流道底部的流速和压力比靠近流道面层的流速和压力分布更均匀些,靠近面层的断面上在喇叭口后部出现了对称的一对漩涡。
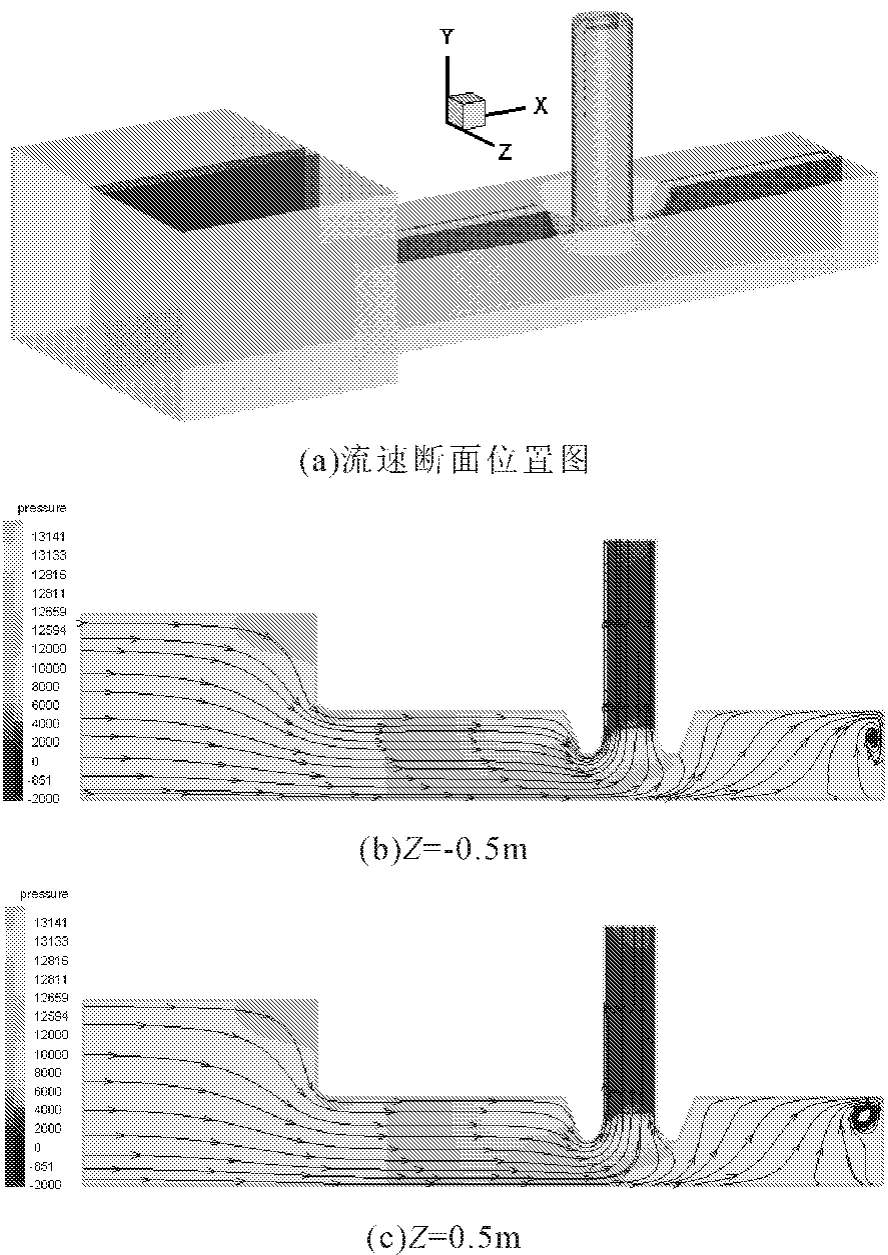
图3 不同纵截面速度等值线图和压力云图

图4 不同水平截面速度等值线图和压力云图
2.4 横向流速
图5是进水流道内从进口到出口不同横截面(从左到右依次编为 1-1、2-2、3-3、4-4、5-5)上的横向流速分布云图,由图5可知,1-1至4-4断面的横向流速均较小,其中3-3断面的横向流速最小,断面最大的横向流速仅为0.08 m/s。由于靠近吸水喇叭口,5-5断面表现为靠近隔墩横向流速大,靠近流道底部和顶部横向流速小的特征。
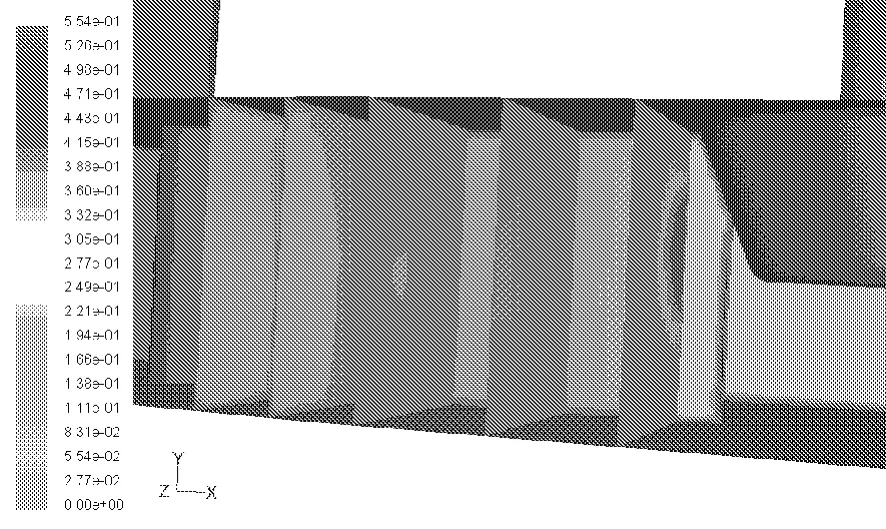
图5 不同横截面上的横向流速云图
2.5 水力损失计算
在计算中,可利用表面积分功能,得到流道进出口的总压,流道水力损失 Δ h由下式算得:
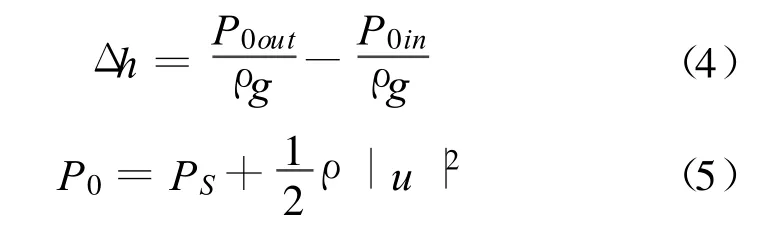
式中:P0out为流道出口的总压;P0in流道进口的总压;PS为表面静压;u为流体速度。
各工况的数值计算水力损失值与流量关系曲线如图6所示。由图6可知,对不同工况的计算表明,进水流道内的水力损失随着流量的增大而逐渐增大,并与流量基本上成二次方关系,这与文献[11]得到的结论相符。
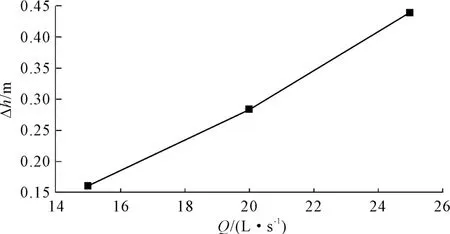
图6 进水流道内水力损失
3 结 语
(1)基于CFD数值模拟,获得了箱形进水流道内部流动的规律,从前池到进水流道直段水流顺直,流态平稳,当进入喇叭口下方时流线急剧弯曲,在进水流道后部死水区有明显的漩涡。
(2)分析了进水流道内不同断面的流速和压力云图,从前池到进水流道,压力分布沿着水流的方向逐渐降低,流速逐渐增大,流态平顺。但在进水流道的后部靠近后壁和喇叭口的位置出现漩涡。
(3)通过对不同工况内水流流动的数值模拟,预测了不同工况下进水流道内的水力损失,其规律是水力损失随着流量的增大而逐渐增大,并基本呈现二次方的关系。
[1]刘超.水泵及水泵站[M].北京:中国水利水电出版社,2009.
[2]刘超,周济人,汤方平,等.低扬程双向流道泵装置研究[J].农业机械学报,2001,32(1):49-51.
[3]周济人,刘超,袁家博,等.大型泵站箱涵式双向进水流道试验研究[J].扬州大学学报(自然科学版),1999,2(4):79-82.
[4]葛强,陈松山,王林锁,等.涵箱型双向流道在船坞泵站应用研究[J].水泵技术,2004,(4):40-43.
[5]葛强,陈松山,王林锁,等.钟形箱涵式进水流道泵装置特性模型试验研究[J].水力发电学报,2006,25(5):129-134.
[6]王林锁,陆伟刚,陈松山,等.“工字型”双向流道泵站装置特性试验研究[J].水力发电学报,2001,20(2):79-85.
[7]LI Yaojun,WANG Fujun.Numerical investigation of performance of an axial-flow pump with inducer[J].Journal of Hydrodynamics,Ser.B,2007,19(6):705-711.
[8]Constantinescu G S,PatelV C.A numericalmodel for simulation of pump-intake flow and vortices[J].Hydr Engrg,ASCE,1998,124(2):123-134.
[9]成 立,刘超,薛 坚,等.基于CFD流动分析的泵站肘形进水流道水力特性研究[J].应用基础与工程科学学报,2008,16(6):891-899.
[10]Rodi W.Turbulence models and their application in hydraulics experimental and mathematical fluid dynamics[C]//Delft:IAHR Section on Fundamentals of DivisionⅡ,1980:44-46.
[11]汤方平,袁家博,周济人.轴流泵站进出水流道水力损失的试验研究[J].排灌机械,1995,(3):13-14.
