顺层岩质边坡稳定性分析与应力监测研究

2011-06-05魏俊奇王礼珍

水利与建筑工程学报 2011年6期

魏俊奇,王礼珍,王丽

(1.陕西省交通建设集团公司靖王分公司,陕西榆林 719000;2.西安公路研究院,陕西西安 710054;3.陕西省交通建设集团公司榆靖分公司,陕西榆林 719000)

0 前言

随着大规模建设由平原区向西部山区挺进,建设过程中不可避免的开挖形成了大量的岩质边坡,对这些人工开挖形成的岩质边坡的稳定性评价越来越成为边坡工程研究领域的重点和热点。顺层岩质边坡是一种较为常见的岩质边坡类型,由于受到平行结构面存在的影响,边坡较易沿结构面滑动而失稳,因此需要对该类边坡的稳定性进行监测。传统的监测方式主要以位移监测为主,但该方法代价高,预警时间滞后,不适合于这类大量存在且失稳具有突发性的边坡类型。本文尝试采用应力监测,即采用锚杆受力监测边坡内部应力变化的方式对顺层岩质边坡的稳定性进行评价,并结合达渝高速一段边坡的现场试验监测成果,评价了该监测方法的可行性[1]。

1 有限元计算模型的建立

首先采用有限元计算方法对边坡易失稳的敏感部位进行分析,为现场应力监测试验确定监测位置。

1.1 采用的方法与屈服准则

采用强度折减的方法求解边坡达到极限平衡状态时的滑动面位置。强度折减法的原理在于通过不断降低岩土体的抗剪强度参数,使边坡逐渐达到极限平衡状态而失稳,计算公式如式(1)、式(2)所示。其中Fs为折减系数,即安全系数;c、φ分别为岩土体的粘聚力与内摩擦角;cs、φs分别为折减后岩土体的粘聚力与内摩擦角。

较为常见的屈服准则多为Mohr-Coulomb准则,但由于Mohr-Coulomb准则在 π平面上的投影存在棱角,所以出现了不同的修正形式,主要有内切圆锥、内角外接圆锥、外角外接圆锥、内切圆锥、等效摩尔圆即等面积圆屈服准则,如图1所示。由于等面积圆的面积等于不等角六边形Mohr-Coulomb屈服强度的面积,可以代替传统的Mohr-Coulomb屈服准则,不仅可以消除Mohr-Coulomb屈服准则的屈服面为不规则六边形截面存在的尖顶和棱角给数值计算带来的困难,而且计算平均误差小、离散度小[2-4]。本文有限元计算采用的屈服准则为徐干成、郑颖人等人的研究得出的Mohr-Coulomb等面积圆屈服准则,表达式如式(3)所示,Mohr-Coulomb等面积圆屈服准则中的参数 α、k的表达式为[5-7]式(4)、式(5)所示,有限元计算中将式(1)、式(2)中对 c、φ折减转化为对α、k折减,如式(6)所示。

式中:I1为应力张量的第一不变量;J2为应力偏量的第二不变量;α、k与介质内摩擦角φ和凝聚力c有关的系数。

式中:c、φ分别为岩土体的粘聚力与内摩擦角。

1.2 有限元计算模型的建立

计算选取的岩质边坡高度为30 m,边坡坡度为1∶0.5,平行的结构面间距分别为 10 m 、5 m、3 m、1 m等4种情况,结构面宽度为0.2 m,倾角为30°。并采用的数值计算软件MSC.Marc软件进行计算,计算网格在结构面位置处加密,在岩体位置处则划分较为稀疏。计算采用的本构关系为摩尔库伦等面积圆屈服准则,由于岩石强度较高,所以仅在计算过程中不断降低结构面位置处的岩土体强度参数,使边坡达到失稳,此时计算不收敛。计算模型分析边坡破坏形式的有限元网格划分图如图2所示,计算所选择的参数见表1。

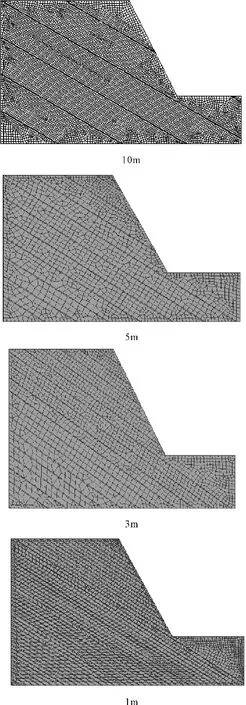
图2 不同结构面间距的有限元网格划分图

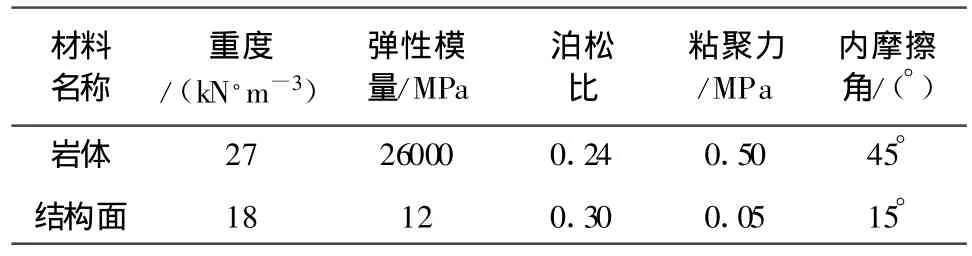
表1 计算采用的材料参数

2 计算结果分析

图3 边坡失稳时的滑动面图

从图3中可以看出顺层岩质边坡失稳时滑动面位于软弱结构面位置处,其位置为地面以上最接近边坡坡脚处的结构面,结构面间距越小这种趋势越明显,当结构面间距过小时(间距=1 m),破坏区域增大,可以认为顺层的岩质边坡失稳时都是在最接近坡脚处的结构面处出现破坏,该处为稳定性敏感部位,采用应力监测时应以该位置处为主。

岩块内部由于粘聚力较大,岩块自身很难出现剪切破坏,而软弱结构面处由于抗剪强度较低所以破坏位置处出现在岩块与结构面的交界处(见图4(a)),在交界处维系 G·sinα与τ的力学关系,当 τ=G·sinα,边坡处于极限平衡状态。其中G=0.5·ρ·a·b·|sinβ|(取岩块的厚度为 1 m),τ=c+σ·tanφ。对同一边坡可以认为边坡体材料是各项均值同性的,即 ρ、β、τ的值是固定的,在 G·sinα中其值随着a、b、sinα的变化而变化。对于顺层岩质边坡可近似认为其边坡结构面之间是平行关系,由图4(b)中可知 Δ OAD 的重心位置为O1,Δ OBC的中心位置O2在OO1的延长线上,可以得出二者与节理面的夹角均为90°-α,则sinα的值是不变的。G·sinα只是与a、b有关的物理量,随着a、b的增大而增大。在临空面以上最近于坡脚处的结构面处的a、b值最大,从而产生的下滑力也是最大的,最容易在该处出现滑塌。

以往对公路岩质边坡一般采用测斜管位移监测的形式,该方法具有明显的滞后性,即监测到大的位移变形时边坡已经破坏,无法及时加固。以上的理论分析结果表明和顺层岩质边坡破坏息息相关的物理量应该是边坡岩体的受力而不是变形。本文有鉴于此采用在顺层边坡结构面位置处布设测力锚杆进行受力监测,即在锚杆上焊接钢筋计进行应力量测的方法,通过应力的变化来评价边坡的稳定性[7-9]。

图4 几何计算简图

3 现场测试数据分析

达渝高速铜锣山隧道出口处的一段岩质高边坡为典型的顺层岩质边坡,边坡高22.8 m,为三级边坡,坡度均为1∶0.75,由于该边坡的结构面倾角为30°,与坡面倾角相差不大,故岩层在坡面出露位置不多,结构面间距为1.6 m;监测锚杆与水平面夹角为20°,位置均在每级边坡最近于坡脚处的结构面上方,锚杆直径为28mm,钢筋计布设位置约为距锚头1 m、3 m、5 m(如图5所示),通过对该边坡的稳定性进行长期的监控分析,评价该边坡的安全状况。

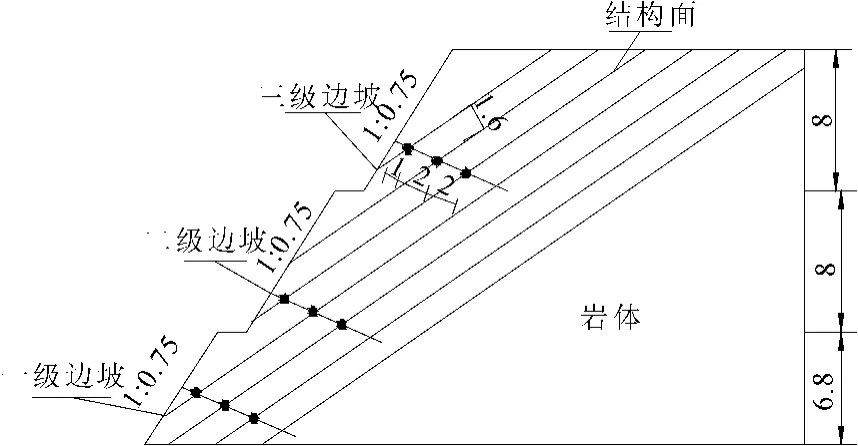
图5 钢筋计布设图

现场试验的结果如图6所示,监测结果显示钢筋计的应力均是在前40 d内出现较大的变化,一级边坡变化最明显的1 m深度位置处锚杆轴力由0变化为23MPa;二级边坡变化最明显的1 m深度位置处锚杆轴力由0变化为11MPa;三级边坡变化最明显的1 m深度位置处锚杆轴力由0变化为7.7MPa。而在后期基本趋于稳定,一级边坡受力最大的1 m深度位置处锚杆应力稳定为30.6MPa左右;二级边坡受力最大的1 m深度位置处锚杆应力稳定为15MPa左右;三级边坡受力最大的1 m深度位置处锚杆应力稳定为19.6MPa左右。这是由于边坡卸荷作用影响下,内部应力进行一定的调整,当应力调整完成时,边坡趋于稳定,此时监测数据也趋于稳定。每级边坡位于最近于该级边坡坡脚处、且在地面或平台以上的结构面位置处监测锚杆的应力最大,这与数值计算、理论分析的结果相吻合,一级边坡钢筋计应力最大,最大值为30.6MPa,小于钢筋设计抗拉强度300MPa,表明该边坡在开挖后内部应力变化完成后基本趋于稳定状态。