基于模糊积分多元决策模型的桩基础选型优化*

祝彦知，禹 光，程 楠

(1.中原工学院建筑工程学院，河南郑州450007;2.中讯邮电咨询设计院有限公司郑州分公司，河南 郑州450007;3.郑州大学信息工程学院，河南郑州450052)

在工程实践中，经常遇到一些多目标决策问题，设计方案优选是常见问题之一，在这类决策问题中，一般有多个决策人员对多方案从多个目标进行评价和选择。对这些目标的评价，有些目标是可以得到定量值(如工期、造价等)，而有些目标则较难得到定量值(如技术难度、环境因素等)，决策人员往往只能对这些目标给出定性的估计和评判。由于实际问题的复杂性及客观存在着的模糊性，使方案优选问题存在着模糊性，在这种情况下，若把模糊数学中的隶属度理论运用上去，问题将得到改善。

模糊决策作为模糊数学的一种具体应用方法，最早是由我国学者汪培庄教授［1］提出的。由于其数学模型简单，容易掌握，对多因素、多层次的复杂问题评判效果比较好，并得到广泛的应用。例如阮连法等［2］应用模糊方法进行设计方案比选;胡国祥等［3］应用模糊优选理论选择基础工程方案;赵可、冉立平［4］应用模糊综合评判进行桩基础设计方案优选，并通过工程实例说明该法的有效性;李刚［5］应用模糊综合评判进行桩基础设计方案优化选择;肖盛燮等［6］对模糊综合评判方法在土木及水利工程中的应用进行了系统研究。

对于系统状态结构因素复杂的庞大决策系统，最简单、实用的方法是首先将其合理划分成决策单元，并根据其间的逻辑关系使其层次化，然后构造各决策单元的决策指标体系，在此基础上，对各决策指标属性进行量化处理，最后对决策单元内决策指标进行合成处理。其中，决策单元内指标之间的逻辑合成技术以及具有层次性逻辑结构关系的决策单元之间的合成技术是顺利完成整个决策过程的关键。

桩基础选择要综合考虑各种因素，在桩基础工程实践中，开发了大量的各式各样的桩型，而且一些新的桩型还在不断地涌现。对于某一个具体的工程而言，采用什么桩型是一个需要慎重对待的问题。成功的桩基设计应该尽可能选用技术性能更好、经济效益更高以及适合现有施工条件的桩型。

为了在桩基础选型优化中综合考虑各种定性、定量因素的影响及各指标的模糊性特征，获得经济上合理、技术上可行的最优桩型，笔者认为，应用分层模糊积分多元决策模型［7］无疑是一条新的途径。

1 基于模糊积分多元决策的桩基选型优化原理

在文献［7］中根据模糊积分的有关理论，首先给出了满意度的定义和计算公式，进而对基于模糊测度的模糊积分加以改进，推导出有限集合上的分层模糊积分多元决策模型。模糊测度的特性在于不必要满足通常测度中的可加性仅需满足单调性即可。因此，用直观的模糊测度去度量模糊事件，使得模糊测度作为测量人们主观意向性的测度既具有理论价值又具有实际价值，从而可以更方便地从理论上研究多元决策问题。

有关模糊测度和模糊积分的定义、有限集合上模糊积分多元决策模型及分层模糊积分多元决策模型的基本理论详见文献［7］，应用模糊积分多元决策模型进行桩基础选型优化的基本原理与步骤如下:

(1)取所有待优化的桩基础方案为备择对象集V，V={V1，V2，…，Vq，…，Vl}，共有l个桩基础方案有待选择，Vq代表第q个桩基础方案，列出影响桩基础方案优选的各个侧面的所有单因素指标集X(因素集)，即 X= {x1，x2，…，xi，…，xn}，xi代表第i个单因素指标。

(2)作因素集X的P划分，得X/P={X1，X2，…，Xj，…，Xm}，记Xj={xj1，xj2，…，xjk，…，xju}，P划分的多少需要视具体问题的性质而定，一般可分为两层即可，第一层根据影响桩基础方案的指标特征将指标分成若干大类，第二层为各类指标中所包含的详细条目。P划分完成后，聘请有经验的专家或工程技术人员对X/P中的每一因素集合Xj和Xj中的xjk(k=1，2，…，u)给出其模糊测度。

(3)利用文献［7］给出的满意度公式计算各备择对象Vq(q=1，2，…，l)中各因素指标的满意度值，得到应用模糊积分多元决策模型进行桩基础方案优选的计算模式:

计算X/P中的每一因素集合Xj的Ej(j=1，2，…，m)，其中，

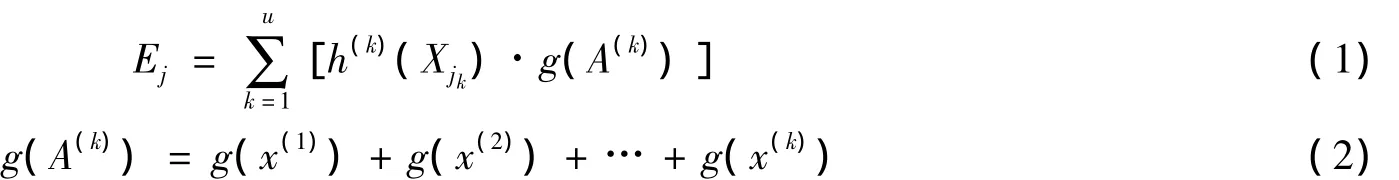
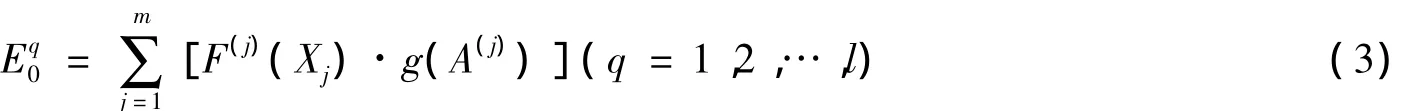
2 实例分析与讨论

为了验证上述计算模型的合理性，并便于同文献［5］的结果进行比较，以某房地产公司开发项目为例进行分析。该项目位于某市中心，周边为密集居民区，为了早日发挥项目经济效益，要求工期尽量短，施工时尽量减少噪音和污染，根据该工程地质条件较差的特点，考虑有静压PHC管桩、预制方桩、沉管灌注桩、钻孔灌注桩、人工挖孔桩五种桩型。根据该工程具体情况，确定以方案的工期、造价、环境、技术作为评价因素，邀请10名设计、施工、监理等方面专家进行方案评价。5个方案的4个因素指标值见表1，其中工期、造价为经测算后的定量指标。

首先作因素集 X={x1，x2，x3，x4}的 P 划分，得 X/P={X1，X2}，其中 X1={x1，x2}，含两个单因素指标，表示待优选桩基方案经济指标中的工期和造价指标，X2={x3，x4}，含两个单因素指标，表示待优选桩基方案指标中的环境和技术指标。根据对影响决策的各因素指标的相对重要程度进行分析，经10位该领域的专家综合评定，确定出各因素的模糊测度值(如表2所示)。

表1 各桩基方案因素指标

表2 因素集P划分和各因素模糊测度g值表

针对一个具体的工程项目，可供选择的桩基础方案有很多种，而且影响桩基础选型的因素往往会很多。因此，采用基于模糊积分多元决策的桩基础选型优化的计算模型，手工计算相当复杂，随着决策指标的增多，有时甚至难以实现，可以根据上述原理，编制程序进行计算，计算结果见表3、表4。从表4的计算结果可以看出，静压PHC桩为最优决策方案。

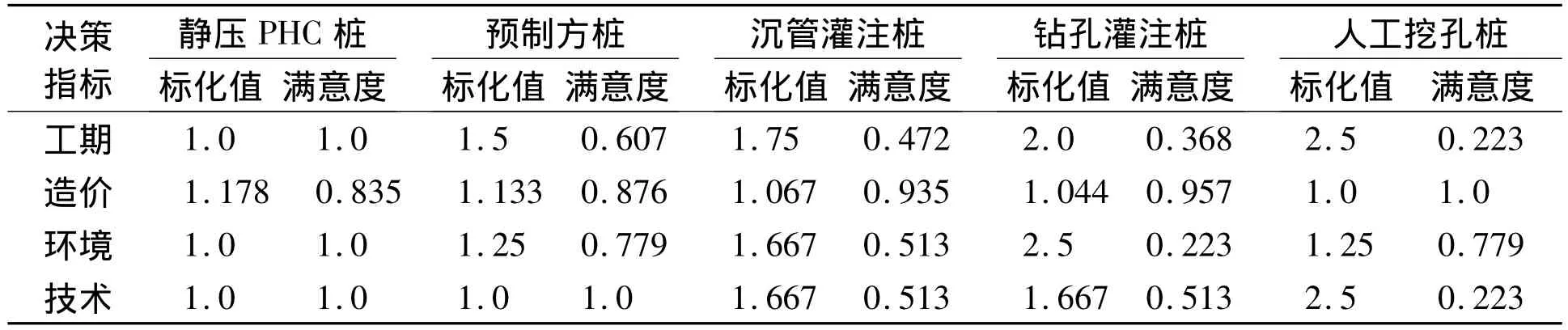
表3 各桩基方案各指标的标化值和满意度

计算分析表明，本文的优选结果与文献［5］中的结果是一致的。但由于该方法是以模糊系统理论中的模糊测度概念为基础，结合模糊积分方法将逻辑加权方法发展为积分合成方法，不仅考虑了待决策系统因素状态特征的重要程度，而且强调了各因素之间的相互关系、相互制约对整个决策系统的影响，使得该方法更具有先进性。

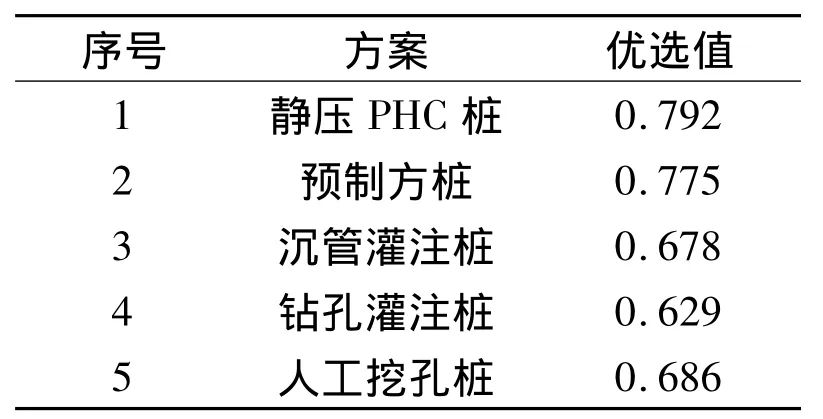
表4 模糊积分多元决策结果表

3 结语

基于模糊积分多元决策的桩基础选型优化模型，用直观的模糊测度去度量模糊事件，在模糊环境下进行桩基础选型优化，充分反映了各桩基础整体指标的相对优劣，可以全面考虑桩基础施工方案选择过程中各种定量与定性因素的影响，若干影响大但权重小的因素也可通过模糊积分对结果产生影响，避免了其它模糊多元决策方法诸如权重大的因素在结果得到反应、而权重小但影响大的因素被屏蔽掉等一些不足。

［1］汪培庄.模糊数学集合论及其应用［M］.上海:上海科技出版社，1983.

［2］阮连法，熊鹰，陶琦.模糊方法在设计方案比选中的应用［J］.建筑经济，1999(9):19－22.

［3］胡国祥，吴峻，周纲.模糊数学优选理论在选择基础方案中的应用［J］.地基基础工程，2003(10):59－61.

［4］赵可，冉立平.基于模糊综合评判的桩基础设计方案优选［J］.建筑管理现代化，2001(1):16－18.

［5］李刚.软土地基上桩基础优化设计［D］.武汉:华中科技大学，2006.

［6］肖盛燮，王平义，吕恩琳.模糊数学在土木与水利工程中的应用［M］.北京:人民交通出版社，2004.

［7］程楠，祝彦知.深基坑支护体系的模糊积分多元决策研究［J］.系统工程理论与实践，2002，22(8):121－126.