含非线性接触碰撞的大口径舰炮弹链柔性铰多体模型

胡胜海，郭彬，邓坤秀，徐鹏

(哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001)

大口径舰炮具有射程远、毁伤能力强的特点，在现代水面舰艇的战术体系中具有重要的地位和作用.目前，我国大口径舰炮技术比较落后，尤其是欠缺相对成熟的供弹系统的支持.某型大口径舰炮在供弹过程中频繁出现由于供弹平台上的炮弹晃动过大造成的扬弹机卡弹问题.为了解决该问题，从动力学的途径对某型大口径舰炮链式供弹平台上的弹链进行研究是十分必要的.由于某型大口径舰炮的弹链在结构上的特殊性，现有的中、小口径炮弹链带模型［1-2］不能很好地反映出其动力学特性.因此，本文应用多体动力学理论［3］建立了某型大口径舰炮的弹链柔性铰多体动力学模型，并在此基础上分析了不同材料的弹筒以及不同片弹簧刚度系数下炮弹的晃动.

1 大口径舰炮供弹系统组成及原理

某型大口径舰炮的供弹系统由链式供弹平台和链式扬弹机组成，如图1所示.供弹平台主要包括供弹链轮、弹链、导向架和导轨，其中弹链由底部装有滚轮的一段链条和两侧装有片弹簧的弹筒装配而成，其结构如图2(a)所示.扬弹机位于弹链的运动轨迹上，主要包括扬弹链轮、扬弹链、固定在扬弹链左、右链边的上、下弹托和底部开口的扬弹筒，其结构如图2(b)所示.某型大口径舰炮的供弹原理是:在供弹链轮的驱动下，供弹平台上的弹链沿导轨步进运动.当炮弹运动到扬弹位置时，弹链运动停止，扬弹链轮正转，下弹托托着炮弹到扬弹筒的中间位置并与上弹托完成炮弹的交接，之后扬弹链轮反转，由上弹托托着炮弹继续扬弹.

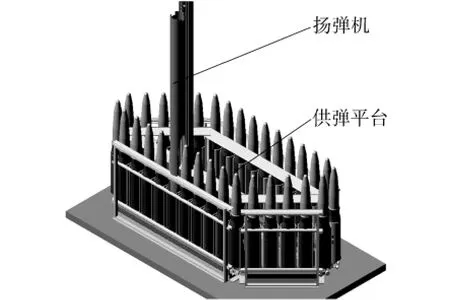
图1 某型大口径舰炮供弹系统Fig.1 Ammunition feeding system of large caliber naval gun

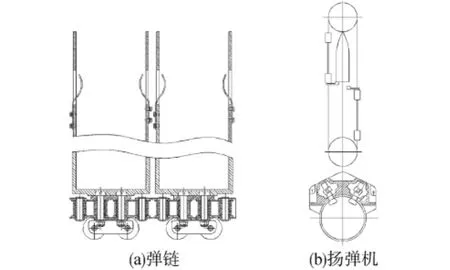
图2 大口径舰炮弹链及扬弹机原理结构Fig.2 Principle structure diagram of ammunition chain and lifter of large caliber naval gun

由于供弹链轮与弹链啮合时存在的多边形效应、啮合冲击以及弹链间歇运动过程中周期变化的惯性力引发剧烈的振动，容易导致炮弹在扬弹位置的位置误差从而引起在扬弹口处卡弹.

2 弹链柔性铰多体动力学模型

在建立弹链动力学模型时需要考虑的主要问题是弹筒上的片弹簧以及弹筒底部链条如何处理.对于片弹簧，较好的方法是利用有限元的方法进行处理，这种方法可以准确地模拟片弹簧的变形以及因此产生的弹性力，但是将极大地增加计算量，因此本文将其考虑成无质量弹簧，在变形量较小并恰当选择刚度系数情况下，并不会产生太大误差.对于链条，普遍的处理方法是将每个链节简化为集中质量，通过弹簧—阻尼器连接各集中质量［4-5］.由于炮弹的质量要比链节大得多并且无法考虑弹筒的高度，因此这种方法不适合用于某型大口径舰炮弹链的动力学建模.相对而言，柔性铰多体模型则可以更好地反映弹链的结构特性.在弹链的柔性铰多体模型中链节为具有一定尺寸形状的刚体，链节间通过六自由度的弹簧—阻尼器柔性铰连接.若将弹簧刚度系数取的足够大，弹筒与链节之间的固定连接也可按柔性铰处理.

2.1 弹链运动学递推方程

对于弹链中任意一个刚体Bi，可在刚体上附一连体基，这样其位姿可以用描述该连体基相对于惯性基的平移位置坐标ri和描述连体基相对于惯性基的转动姿态坐标θi唯一确定，即

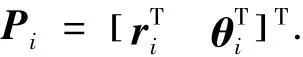
为了分析弹链的运动学，考虑如图3所示的任意2个邻接物体Bi-1和Bi，并在其各自的质心处附一连体基.为了描述方便，将柔性铰与滑动铰、转动铰统一为广义铰的形式.定义外接物体相对于内接物体Bi-1的铰坐标为

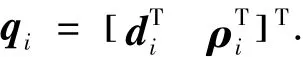
由图3可得到物体Bi-1和Bi的位置和角速度运动学关系:

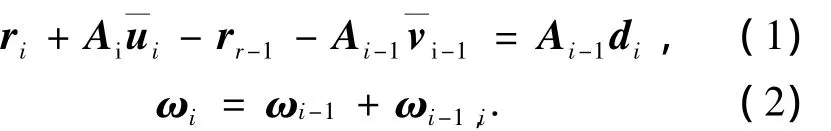
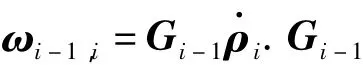
将式(1)、(2)对时间求导可得物体Bi-1和 Bi的速度和角加速度运动学关系:

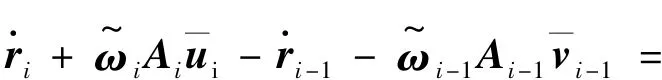
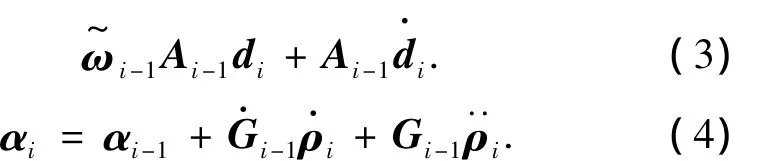
对式(3)再次求导可得物体Bi-1和Bi的加速度运动学关系:

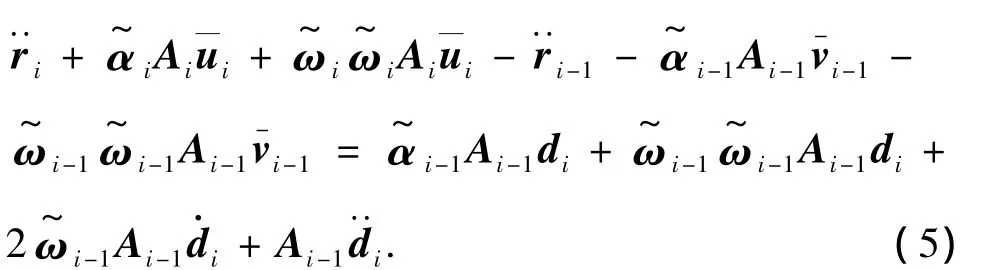
将式(4)、(5)写成矩阵的形式:

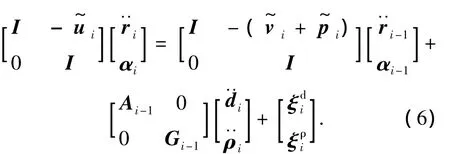
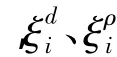
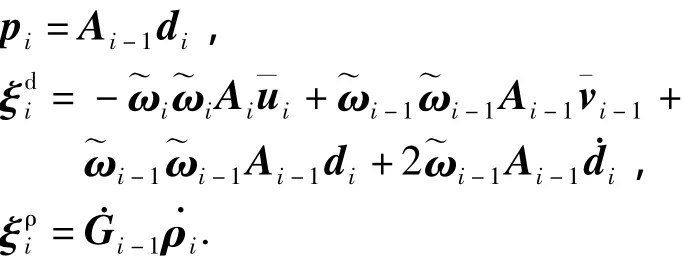
对式(6)进行整理并简化可得

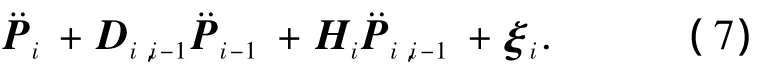
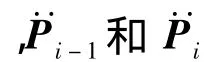
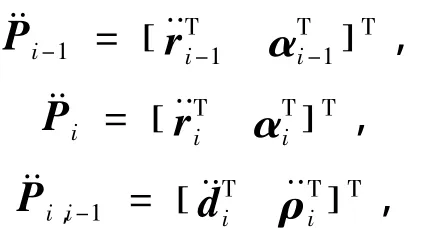
利用式(7)，可写出n个物体递推方程:

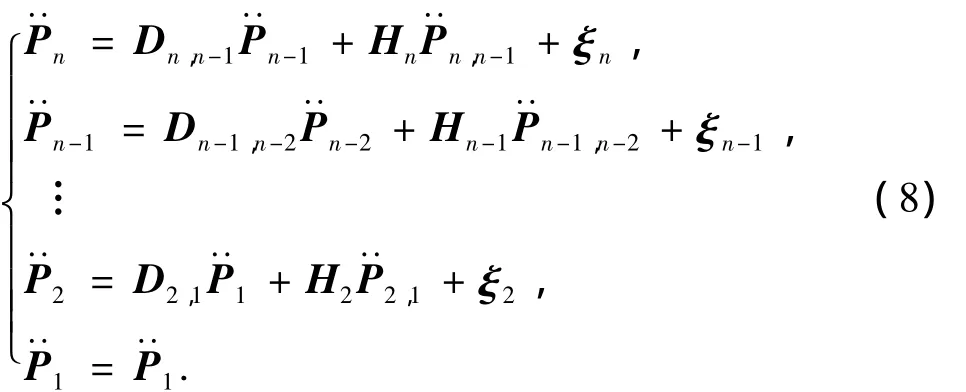
将式(8)写成矩阵的形式:

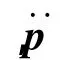
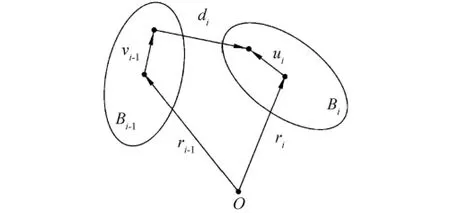
图3 邻接物体的相对运动学Fig.3 Relative kinematics of adjacent bodies

2.2 弹链系统动力学方程

弹链系统的动力学方程可分2个部分建立，炮弹为无约束物体，应用牛顿欧拉方法可直接得出其动力学方程，其外力主要为碰撞力;链条和弹筒间存在运动学约束，其动力学方程需要在牛顿欧拉方法基础上结合前面的运动学递推方程得到

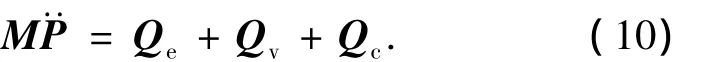
式中:M为质量矩阵，Qe为外力阵，Qv为与速度相关的力阵，Qc为约束力阵.

将式(9)代入式(10)并左乘BT，并注意到BTQc整理可得

当发生接触碰撞时，则在系统动力学方程右侧中的广义力项引入等效接触力，广义力矩阵应更改为

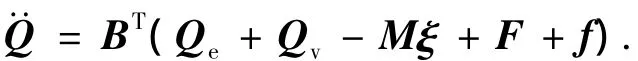
式中:F、f分别为等效接触力和摩擦力的广义力阵.弹链的动力学计算流程如图4所示.

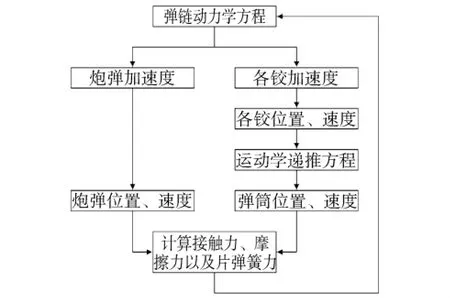
图4 弹链动力学计算流程Fig.4 Dynamic calculation flowchart of ammunition chain

3 含摩擦的弹链接触碰撞分析

某型大口径舰炮的供弹过程中存在多种接触碰撞问题，如滚子与链轮、滚子与导轨、炮弹与导向架以及弹筒与导向架的接触碰撞等，并同时伴随摩擦，而所产生的摩擦力是供弹阻力的主要形式，对弹链的供弹性能有着重要的影响，因此建立考虑摩擦的接触碰撞模型是十分必要的.

3.1 非线性接触碰撞模型

接触碰撞的力学模型可分为2类:1)用弹簧以及阻尼器分别反映物体的变形和碰撞的能量损耗;2)忽略碰撞过程的细节，认为碰撞在瞬间完成，碰撞使速度产生突变.第一类模型在数值计算的实现上较方便，但是最早的第一类模型是线性的，模型存在诸多局限性［6］如:1)在碰撞接触开始时存在非零的阻尼力;2)在接触过程中的恢复阶段，接触力和阻尼力之和有可能出现负值;3)当相对位移为零时，阻尼力出现最大值.针对这些局限性问题，很多学者发展出一种非线性模型，实践表明非线性模型与真实情况吻合程度较理想，因此本文采用非线性的第一类模型进行大口径舰炮弹链的接触碰撞分析.

Hunt和Crossley［7］提出一种非线性弹簧—阻尼模型，碰撞过程中产生的接触力与碰撞点相互侵入的深度和侵入速度之间的关系近似为

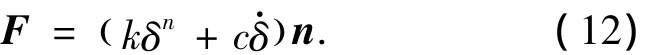
式中:k、c分别为刚度和阻尼系数，n为非线性指数，一般取n=1.5.碰撞力的方向n指向两物体各自表面在接触点处的内法线方向.

对于式(12)中的阻尼系数c，Lankarani和 Nikravesh［8］给出了一种具有迟滞效应的形式:

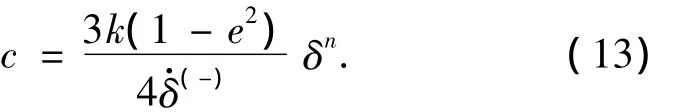
利用式(13)可得含迟滞阻尼的接触力形式:

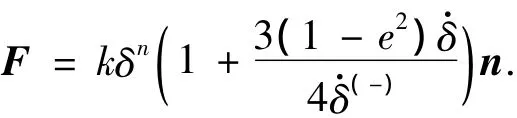
3.2 接触刚度系数的确定

在接触模型中，一个很重要的问题是如何选择恰当的接触刚度系数.接触刚度系数如果取得过小将造成较大的计算误差，过大则容易导致计算失败.弹链柔性铰多体模型中滚子与链轮接触的刚度系数可按以下方法确定［9］.对于滚子与齿沟圆的接触，其穿透量是关于压力载荷的函数:

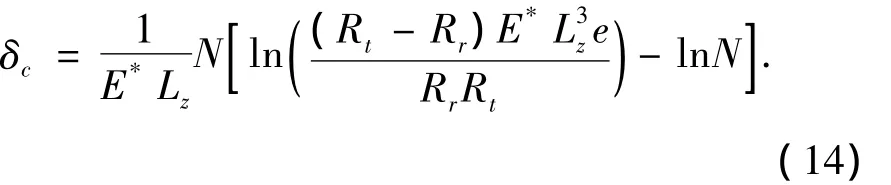
3.3 接触状态的判定

2个物体上可能接触点的相对位置可以用一个间隙函数 Ψ(q，t)表示［10］，假设一个正的小量 ε，如果两物体满足:

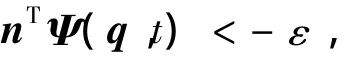
则认为两物体间碰撞开始，需要进一步确定计算接触力所涉及到参数，如侵入深度、侵入速度以及接触法线和切线方向.如果两物体满足:

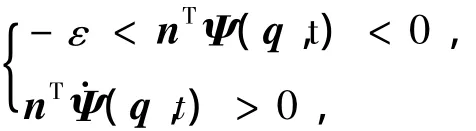
则认为二者间碰撞结束.

3.4 动态摩擦模型

Canudas de Wit等［11］提出的 LuGre摩擦力模型是一个动态的摩擦模型，连续性较好，能更好地描述摩擦的非线性行为.该模型用一个一阶微分方程描述了诸多摩擦现象，如库伦摩擦、预滑动、可变静摩擦力以及摩擦滞后.根据该模型，摩擦力是接触力和速度的函数:

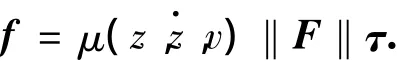
式中:z为状态变量，μ为摩擦系数，τ为与运动速度(趋势)相反的切线方向.

4 不同材料的弹筒和不同片弹簧刚度系数下弹链动力学分析

在弹链动力学方程中一个重要的参数是柔性铰的刚度系数，可按链节销轴与套筒的接触刚度系数确定.由于链节销轴与套筒的接触类似于滚子与齿沟圆的接触，因此其接触刚度系数按式(14)计算.已知弹链材料为40Cr，销轴与套筒接触部分的长度为42 mm，可计算出弹链柔性铰刚度系数kf=542 kN/mm.

根据扬弹筒直径，炮弹的晃动应限制在10mm内.由于两侧导向架可很好地限制炮弹的横向晃动，因此本文主要分析炮弹的纵向晃动.考虑到弹筒和片弹簧是影响炮弹位置精度的2个主要因素，因此分别在弹筒使用不同的材料和片弹簧使用不同厚度的2种情况下进行分析.

第1种情况下片弹簧刚度系数ks取0.1 kN/mm(按弯片弹簧挠度公式计算)，弹筒分别为铝制和钢制，炮弹在扬弹位置的纵向晃动量和片弹簧作用力如图5、6所示，可见使用钢制弹筒情况下炮弹在扬弹位置的初始晃动量约为6 mm，与使用铝制弹筒情况下约13 mm的晃动量相比减小了54%，片弹簧作用力减小了约30%.

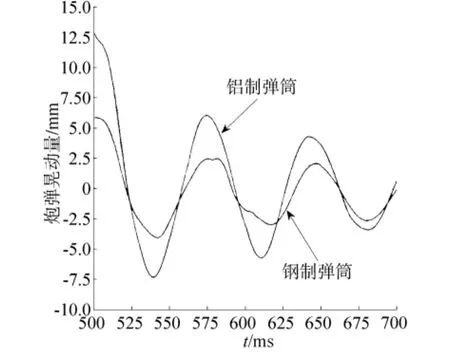
图5 不同材料的弹筒下的炮弹晃动Fig.5 Rocking of shell at shell container with different materials

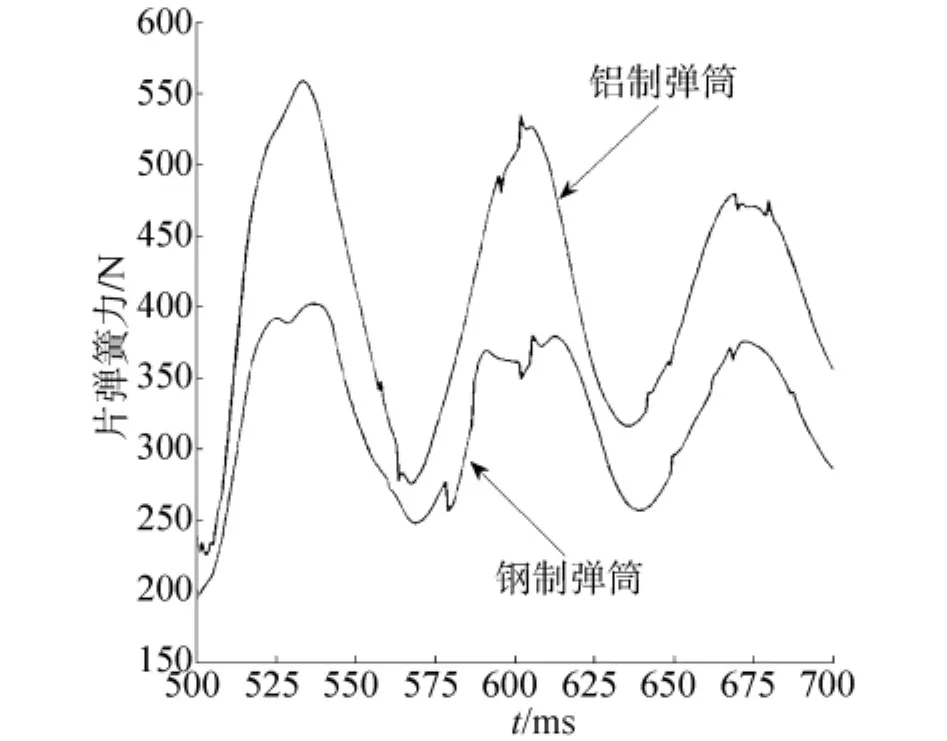
图6 不同材料的弹筒下的片弹簧力Fig.6 Leaf spring forces at shell container with different materials

第2种情况下采用钢制弹筒，按片弹簧厚度的不同，片弹簧刚度系数 ks分别取0.05、0.1、0.2 kN/mm.炮弹在扬弹位置的纵向晃动量和片弹簧作用力如图7、8所示，可见片弹簧刚度系数取0.1 kN/mm时，炮弹在扬弹位置的初始晃动量比刚度系数取0.05 kN/mm时减小了约3 mm，而刚度系数分别取0.1 kN/mm和0.2 kN/mm时，炮弹在扬弹位置的初始晃动量相差不大，但计算时间增加了10%.此外，在不同刚度系数的片弹簧下，由于片弹簧预变形相同，因此其预载荷与刚度系数成正比，这在图8中表现为3条片弹簧力曲线存在偏移.

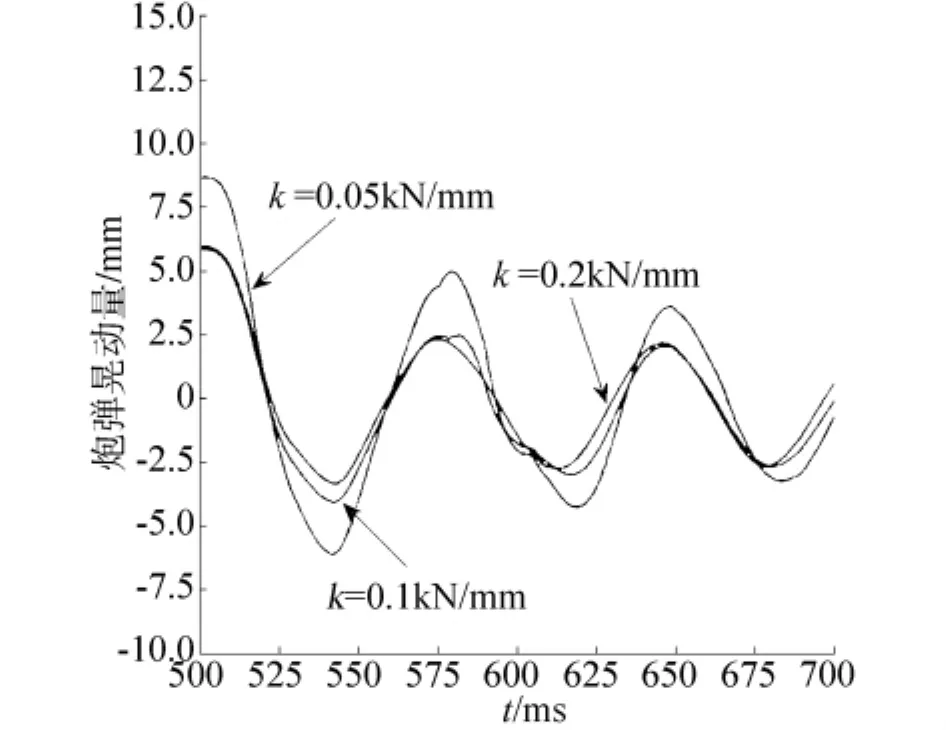
图7 不同片弹簧刚度系数下的炮弹晃动Fig.7 Rocking of shell at leaf spring with different stiffness coefficients

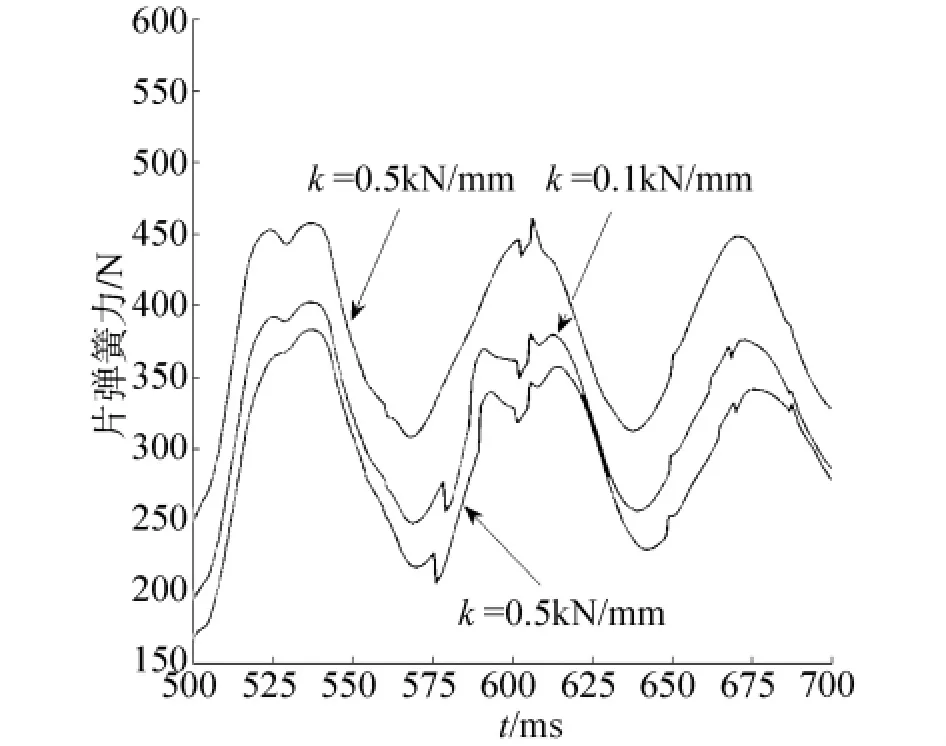
图8 不同片弹簧刚度系数下的片弹簧力Fig.8 Leaf spring forces at leaf spring with different stiffness coefficients

5 结论

本文对某型大口径舰炮在供弹过程中因炮弹晃动过大引起的扬弹机卡弹问题进行了研究，通过比较不同弹筒材料和不同片弹簧刚度系数两种情况下炮弹在扬弹位置的晃动，得到了以下结论:

1)使用钢制弹筒对减小炮弹在扬弹位置的晃动有明显作用，约为使用铝制弹筒情况下的46%;

2)为了减小炮弹在扬弹位置的晃动，应选择厚度较大，即刚度系数较大的片弹簧，但刚度系数增加到某一数值后对炮弹晃动的减小作用并不明显却增加了计算时间，可按其刚度系数为弹链柔性铰刚度系数的0.2‰左右确定片弹簧的厚度.

本文的研究为减小某型大口径舰炮链式供弹平台中炮弹的晃动、提高其供弹可靠性和安全性提供了理论依据.

［1］姜铁牛.30 mm自动炮弹链供弹特性匹配［D］.南京:南京理工大学，2007:1-3.

JIANG Tieniu.The matching problem on the feeding characteristic of 30mm automatic gun［D］.Nanjing:Journal of Nanjing University of Science and Technology，2007:1-3.

［2］章定国.航炮弹链中的碰撞动力学［J］.南京理工大学学报，1995，19(3):210-213.

ZHANG Dingguo.The impact dynamics in the system of bullet chain of airplane gun［J］.Journal of Nanjing University of Science and Technology，1995，19(3):210-213.

［3］SHABANA A A.Computational dynamics［M］.2nd ed.New York:Wiley Interscience Publication，2001:443-456.

［4］XU Lixin，YANG Yuhu，CHANG Zongyu，et al.Dynamic modeling of a roller chain drive system considering the flexibility of input shaft［J］.Chinese Journal of Mechanical Engineering，2010，23(3):367-374.

［5］XU Lixin，YANG Yuhu，CHANG Zongyu，et al.Clearance influence on dynamic response of intermittent roller chain drive［J］.Chinese Journal of Mechanical Engineering，2010，23(6):699-708.

［6］刘才山，陈滨.多柔体系统碰撞动力学研究综述［J］.力学进展，2000，30(1):7-14.

LIU Caishan，CHEN Bin.A global review for the impact dynamic research of flexible multibody systems［J］.Advances in Mechanics，2000，30(1):7-14.

［7］HUNT K H，CROSSLEY F R E.Coefficient of restitution interpreted as damping in vibroimpact［J］.Journal of Applied Mechanics，1975，42(2):440-445.

［8］LANKARANI H M，NIKRAVESH P E.A contact force model with hysteresis damping for impact analysis of multibody systems［J］.Journal of Mechanic Design，1990，112(3):369-376.

［9］HU Shenghai，GUO Bin，DENG Kunxiu，et al.An efficient contact analysis for roller chain［C］//2011 International Conference on Mechatronics and Intelligent Materials.Zurich:Trans Tech Publications，2011:290-294.

［10］盛秋峰，洪嘉振，刘铸永，等.含接触碰撞的变拓扑系统动力学仿真［J］.上海交通大学学报，2008，42(8):1222-1237.

SHENG Qiufeng，HONG Jiazhen，LIU Zhuyong，et al.Dynamic simulation of multibody system with variable topology［J］.Journal of Shanghai Jiao Tong University，2008，42(8):1222-1237.

［11］刘丽兰，刘宏昭，吴子英，等.机械系统中摩擦模型的研究进展［J］.力学进展，2008，39(2):201-213.

LIU Lilan，LIU Hongzhao，WU Ziying，et al.An overview of friction models in mechanical systems［J］.Advances in Mechanics，2008，39(2):201-213.