含马氏链的股票指数模糊随机预测模型

李嵩松，惠晓峰

(哈尔滨工业大学管理学院，黑龙江哈尔滨150001)

股票指数的涨跌可以反映出股票市场的整体走势，所以对于股票指数的预测一直是研究人员、机构投资者以及普通股民们最关注的热点之一.股票指数的预测方法有很多种:时间序列分析(time series analysis)［1］、多元回归模型(multiple regression models)［2］、人工神经网络(artificial neural network)［3］和遗传算法(genetic algorithms)［4］等.其中人工神经网络方法，需要市场指数、技术指标和市场的基本因素等作为输入信息，而这些信息是很难界定和选择的［5］，因此影响了该方法的发展;在遗传算法中，股票数据巨大的噪音和广阔的维度也使其发展受到了限制.

相反地，由于马尔可夫过程具有无后效性特征，该特征能使输入的数据和处理量大幅缩减，并且马尔可夫过程可以描述一般的股票市场情况［6］，因此马尔可夫预测方法被广泛应用在股指预测中:HASSAN和NATH运用隐马尔可夫模型(hidden Markov model)预测了航空公司的股票价格［7］;BAUERLE和RIEDER在对股价和利率的最优组合研究中改进了马尔可夫方法［8］.近年来，模糊随机方法(fuzzy stochastic method)被应用在多个领域［9］，在股指预测方面，WANG利用该方法提出了一种模糊随机预测模型［10］，并进行了实证研究，得到了令人满意的预测结果［11］.本文引入马尔可夫链的概念到模糊随机预测模型当中，改进了预测参数，并对沪深300指数数据进行了实证研究.

1 股票指数预测模型

1.1 模糊随机预测模型

股票在股票市场上进行交易时，股票价格是在不停变动的，这种情况被认为是一种随机过程.用随机变量Xt表示在t时刻的股票价格;Pn用来表示在n=0，1，2，…时，随机变量Xt上涨或者下跌的概率.如果Xt=n，从时间t经过很短的时间变化Δt到时间(t+Δt)，对于股票价格上涨或下跌有如下假设:1)股票价格上涨的概率是与Δt成比例的，表示为bnΔt;2)股票价格下跌的概率是与Δt成比例的，表示为dnΔt;3)上涨和下跌是不相关的随机事件;4)bn和dn是与n成比例关系的，表示为bn=λn和dn=μn，当n=1时，λ和μ分别表示单位时间股票价格上涨或者下跌的概率.

根据以上假设，可以得到关于Pn(t)的表达式:

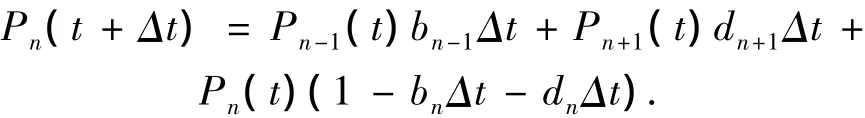
由此，Wang等［11］提出了一种实时股票价格模糊随机预测的模型:

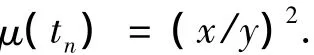
式中:x表示指定时间的目标价格，tn表示指定时间的那一天，y表示在同一天指定时间中的最高价格.

1.2 马尔可夫链方法

马尔可夫链(Markov chain)是数学中具有马尔可夫性质(Markov property)的离散时间随机过程.该过程中，在给定当前知识或信息的情况下，只有当前的状态用来预测将来，过去(即当前以前的历史状态)对于预测将来(即当前以后的未来状态)是无关的.马尔可夫性质的数学表达为

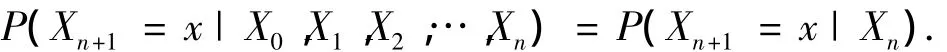
式中:随机变量X0、X1、X2、…、Xn分别表示的是在时间0、1、2、…、n下X的状态，x为过程中的某个状态，Xn+1对于过去状态的条件概率分布仅是Xn的一个函数，与X0、X1、X2、…、Xn-1都无关.系统在Xn=i这个状态的概率用ai(n)表示;系统由状态Xn=i经过一步转移到达状态Xn+1=j的概率，称为一步转移概率，记为pij.状态空间S里的随机过程{Xn，n≥0}如果满足下列条件，就是一条马尔可夫链:如果i和j都属于状态空间S，那么

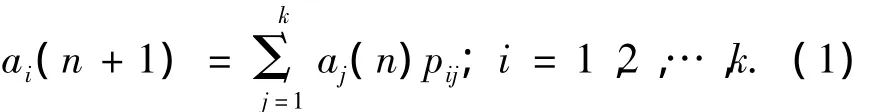
并且ai(n)和pij都满足以下条件:

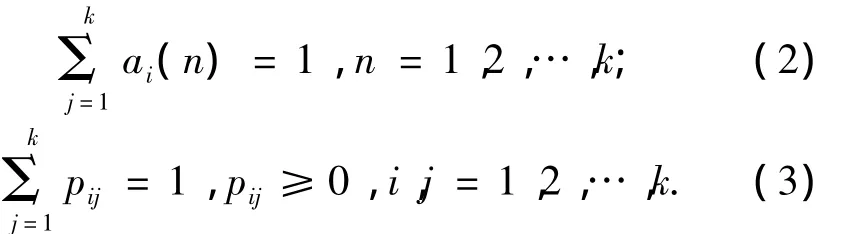
1.3 预测模型的改进

由于股票指数的变动是一种随机过程，并且满足马尔可夫链的无后效性特征，因此将马尔可夫链的概念引入到模糊随机预测模型当中，用以改进其中的预测参数.

将股票指数每日数据按小时分成组，用随机变量Xn来表示在第n小时股票指数的状态.Xn=1表示股票指数上升状态;Xn=2表示股票指数下降状态，其中n=1，2，….yi(n)表示在第n小时股票指数状态上涨(i=1)或下跌(i=2)的概率，即yi(n)=P(Xn=i).用pij表示股票指数从某小时的i状态(Xn=i)，转移到下个小时的j状态(Xn+1=j)的概率，即转移概率pij=P(Xn+1=j|Xn=i).Xn+1只与上一个状态Xn和转移概率pij有关，与之前的状态Xn-1、Xn-2、…都无关，因此根据以上关系式，可以得到如下表达式:

把从一个特定小时的状态i到下一个小时的状态j的变化率用rij来表示，其数学表达式为

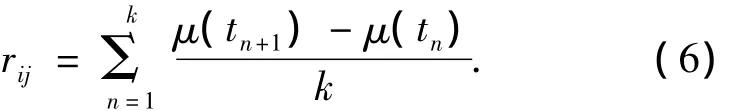
函数μ(tn)被定义为

式中:x表示指定时间的股票指数，tn表示指定时间的那一天，y表示在同一天各个指定时间中最高的股票指数.

由此，根据式(4)和(5)可以得到预测模型参数r的表达式:

2 沪深300指数预测的实证研究

2.1 样本数据

沪深300指数是由上海证券交易所和深圳证券交易所联合编制的，共选取300只A股作为样本，其中沪市有179只，深市有121只.沪深300指数样本选择的标准为规模大、流动性好、交易活跃的主流投资股票，覆盖了沪深市场六成左右的市值，具有良好的市场代表性.因此对沪深300指数的预测研究对掌握整个A股市场的走势具有很大帮助.本文选取了沪深300指数的整点分时(60 min)数据，数据期间为2009年1月1日至12月31日，全年共开市244天，如表1 所示:每天分选 09:30、10:30、11:30、14:00 和15:00共5个时刻，分时数据共1 220个.

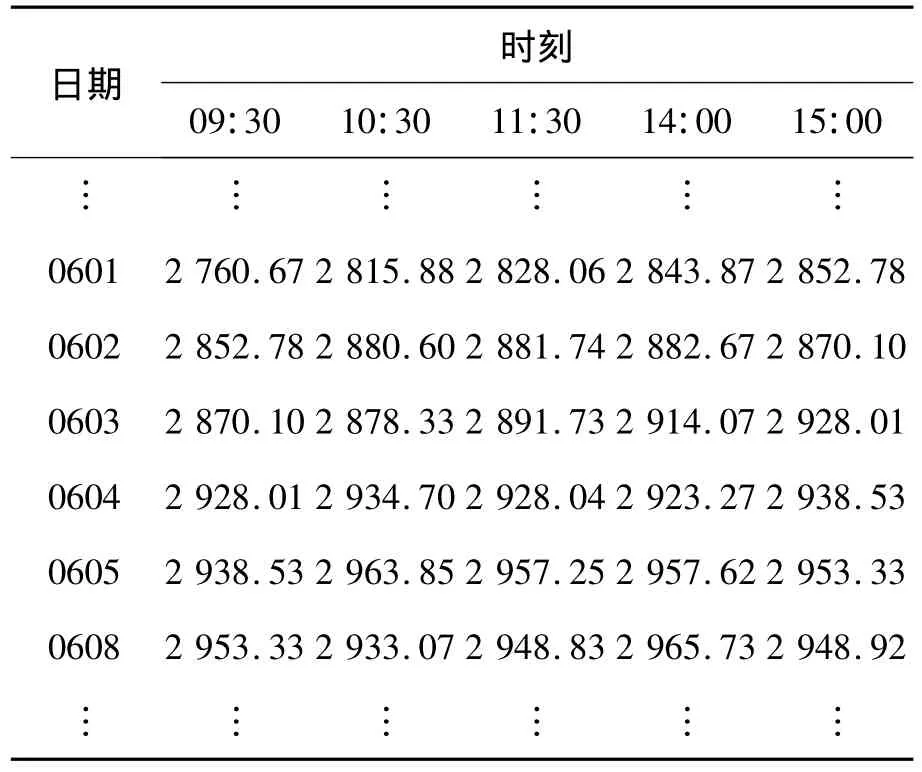
表1 沪深300指数60 min整点数据Table 1 60 minutes data of HS300 stock indexes

2.2 股票指数上涨或下跌的概率

本节根据式(4)和(5)，将计算出股票指数上涨或下跌的转移概率p11、p21、p12和p22.

在表示下一时刻股票指数上涨或下跌情况的表2中，“1”表示下一时刻股票指数上涨;“0”表示下一时刻股票指数下跌，即如果当前时刻的股票指数大于或等于前一时刻的股票指数，那么就用“1”表示;如果当前时刻的股票指数小于前一时刻的股票指数，那么就用“0”来表示.例如在表1中，0601在10:30的股票指数是2 815.88，大于同一天09:30股票指数2 760.67，因此，在表2中，0601在10:30处用“1”表示股票指数比上一时刻09:30上涨.

转移概率p11表示上一时刻股票指数上涨并且这一时刻股票指数也上涨的概率，可以通过用表2中指定时间段内出现(1，1)的次数除以这一时间段内的数据总数来获得;p12表示的是上一时刻股票指数上涨但这一时刻股票指数却下跌的概率，可以通过用表2中指定时间段内出现(1，0)的次数除以这一时间段内的数据总数来获得;p21表示的是上一时刻股票指数下跌但这个时刻股票指数却上涨的概率，可以通过用表2中指定时间段内出现(0，1)的次数除以这一时间段内的数据总数来获得;p22表示的是上一时刻股票指数下跌并且这一时刻股票指数也下跌的概率，可以通过用表2中指定时间段内出现(0，0)的次数除以这一时间段内的数据总数来获得.举例说明:假设只计算0601～0605这5天的转移概率，表2中在09:30～10:30这个时间段内出现(1，1)的次数为4次，数据总数为5个，因此得到p11=4/5=0.8.

表3显示的是2009年全年244个开市日，按每日4个时段分别计算得到的转移概率p11，p21，p12和p22.

表2 下一时刻股票指数上涨或下跌情况Table 2 Stock index rising or falling in the next time

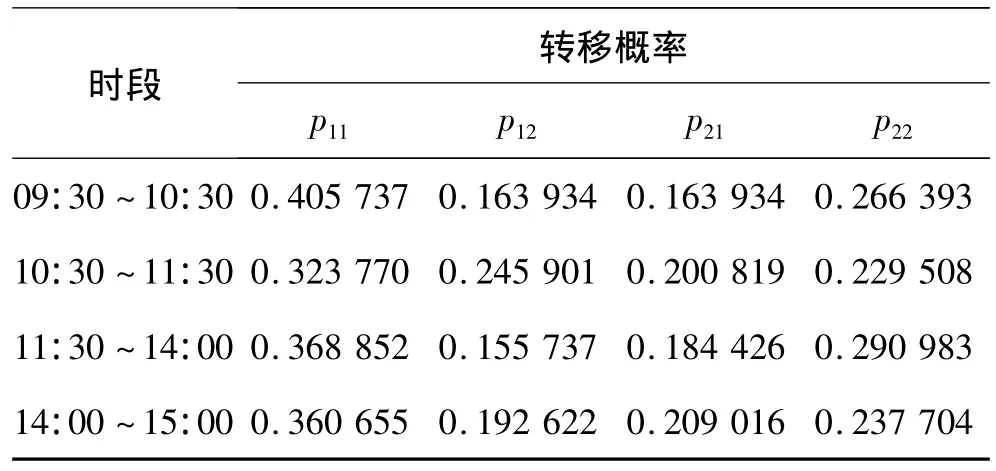
表3 每个时段的转移概率Table 3 Transition probabilities in each time period

2.3 预测参数

根据式(7)所定义的μ(tn)，举例说明:0602这一天5个时刻的股票指数如表4所示，其中最高值出现在14:00这个时刻，股票指数为2 882.67，即y=2 882.67，因此在09:30 这一时刻的 μ =(2 852.78/2 882.67)2=0.979 369 8.以此类推可以得到每天5个时刻分别的μ值.

表4 μ的部分计算结果Table 4 A portion of

预测模型中的rij表示的是股票指数从状态i到状态j的变化率，通过前面计算出的μ值以及式(6)可以分别计算出股票指数变化率的所有情况r11、r21、r12和r22，计算结果显示在表5中.

由于已经计算出转移概率p11、p21、p12、p22和变化率r11、r21、r12、r22，根据式(8)，可以计算出预测参数r，结果显示在表6中.

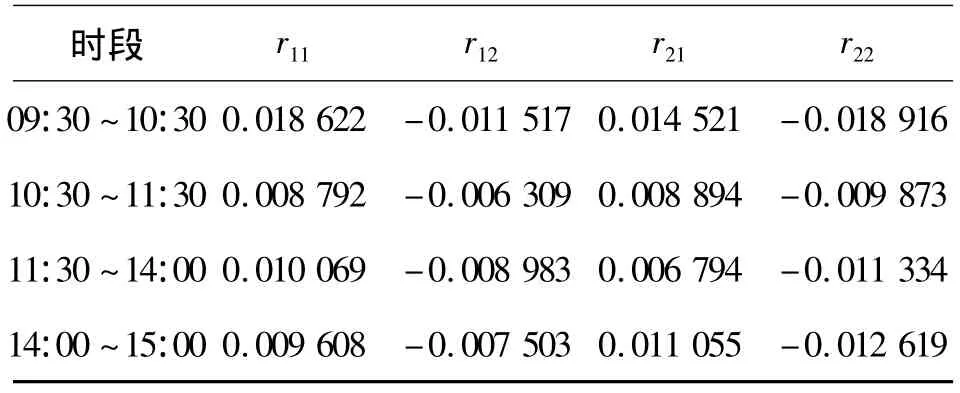
表5 股票指数变化率Table 5 Change rates of stock index

表6 预测参数rTable 6 Parameter r

2.4 预测结果

根据预测模型Xn+1=Xner，分别用改进前的预测参数和改进后的预测参数对2009年全年的沪深300指数60 min分时数据进行预测，部分预测结果、相对误差和优劣比较情况显示在表7中.

表7 预测值和相对误差Table 7 Predicted values and deviations

用改进后的预测模型预测得到的结果中，相对误差最大值是2.907×10-2，比用改进前的预测模型预测的结果中相对误差最大值4.023 ×10-2减小1.115 ×10-2;用改进后的预测模型预测得到的结果中，相对误差最小值是1.549×10-6，比用改进前的预测模型预测的结果中相对误差最小值1.819 ×10-5减小1.664 ×10-5.在优劣比较中，如果用改进后的预测模型预测得到的预测值相对于真实值的相对误差，小于或等于用改进前的预测模型预测得到的预测值相对于真实值的相对误差，即改进后的预测模型的预测值优于改进前的预测模型的预测值，那么就用“1”表示;相反则用“0”表示.经过统计比较，在2009年全年1 220次预测值的相对误差比较中，共得到864个“1”，有71%的改进后模型预测的预测值优于改进前模型的预测值.此外，2009年沪深300指数的真实值与改进后模型预测值的对比情况用图1显示.从图1中可以看出，采用改进后模型预测得到的预测值与沪深300指数的真实值十分接近.

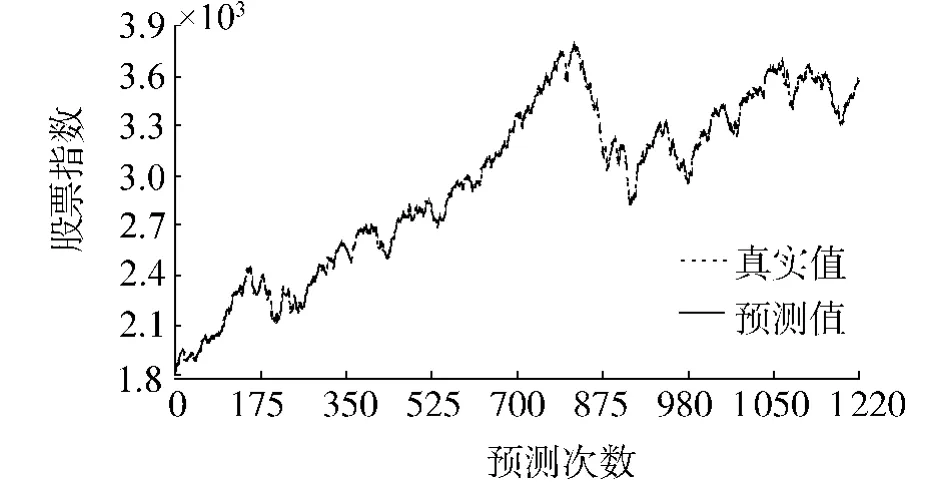
图1 沪深300指数真实值与预测值Fig.1 HS300 stock index true values and predicted values

3 结束语

通过将马尔可夫链概念和转移概率引入到模糊随机预测模型当中，改进了模糊随机预测模型的预测参数，并以2009年沪深300指数为样本进行了实证研究.研究表明，考虑股票指数上涨或下跌的概率以及从上一状态转换到下一状态的转移概率后，计算得出的预测参数可以更好地反映出股票指数变动的真实性;并且得到，改进参数后的预测模型预测得到的数据比未改进参数的预测模型预测得到的数据更接近真实的股票指数的验证结果.然而由于股票市场的复杂性和不确定性，很难准确描述股票指数的变动情况，所以还有很多问题值得进一步研究，比如基本面信息对所提预测模型的影响等.

［1］LENDASSE A，BODT E，WERTZ V.Non-linear financial time series forecasting—application to the Bel 20 stock market index［J］.European Journal of Economic and Social Systems，2000，14(1):81-91.

［2］胡蓉.基于多输出支持向量回归算法的股市预测［J］.云南民族大学学报:自然科学版，2007，3(16):189-192.

HU Rong.Application of multi-output support vector regression in stock market index forecasting［J］.Journal of Yunnan NationalitiesUniversity:NaturalSciencesEdition，2007，3(16):189-192.

［3］FILIPPO C.Forecasting price increments using an artificial neural network［J］.Advances in Complex Systems，2001，4(1):45-56.

［4］KORCZAK J，ROGER P.Stock timing using genetic algorithms［J］.Applied Stochastic Models in Business and Industry，2002，18(3):121-134.

［5］YAO J T，TAN C，POH H.Neural networks for technical analysis:a study on KLCI［J］.International Journal of Theoretical and Applied Finance，1999，2(8):221-241.

［6］ZHANG Q.Stock trading:an optimal selling rule［J］.SIAM Journal on Control and Optimization，2002，40(1):64-87.

［7］HASSAN M R，NATH B.Stock market forecasting using hidden Markov model:a new approach［C］//Proceedings of 5th International Conference on Intelligent Systems Design and Applications.Washington DC，USA，2005，192-196.

［8］BAUERLE N，RIEDER U.Portfolio optimization with Markov-modulated stock prices and interest rates［J］.IEEE Transactions on Automatic Control，2004，49(3):442-447.

［9］LUHANDJULA M，GUPTA M.On fuzzy stochastic optimization［J］.Fuzzy Sets and Systems，1996，81(1):47-55.

［10］CHIANG D，CHOW L，WANG Y F.Mining time series data by a fuzzy linguistic summary system［J］.Fuzzy Sets and Systems，2000，112(5):419-432.

［11］WANG Y F.On-demand forecasting of stock prices using a real-time predictor［J］.IEEE Transactions on Knowledge and Data Engineering，2003，15(4):1033-1037.