从Shannon信息论到认知信息论

卢侃

(哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001)

Shannon信息论主要是通信的信息理论.但所提出的＂信息就是不确定性的消除＂这一基本论点，不仅适用于描述通信的过程，也适用于描述认知的过程.因为，人类每次认知的结果，都是对于外界事物信息的不确定性的减少或完全消除.透沏地说，通信也属于一种间接的认知，即将一些人的认知传给另一些人使之认知而已.

Shannon信息论的精髓在于将通信的内容抽象为信息，赋予信息以数学的形式，将通信过程中的信息加工变为严格的数学运算.如果一个信源的实际信息熵小于其占用的编码空间，那么，就可以对信源参数做一种编码压缩的数学变换，使新编码所占用的空间可以压缩到接近甚至等于原始信源的信息熵.这样，就可以用较少的信道容量完成通信而不丢失信息.如信道中有干扰，则增加相应的监督码量来纠错而保证信息的无损传输.最后在接收端，还要做一种译码的数学反变换以完整地恢复原始信号.这就是Shannon的信源编码和信道编码的基本数学原理［1-2］.

人类认知活动其实也是一种信息加工的活动.原则上说，也是可以用严格的数学运算来加以描述.即类似于Shannon的＂通信的数学理论＂，应该也有一种＂认知的数学理论＂.一旦这个理论建立，认知信息的活动就有了严格的数学模型.将这个模型实用化以后，一个可以做复杂运算的电子计算机就可以实现认知的运算，从而出现真正的模拟人类认知的电子大脑［3］.

1 认知信息加工的原材料、产品和加工的数学实质

1.1 认知信息加工的原材料

人在感知外界时，感觉器官要输入大量的物理或化学刺激(通常称为信号).这些信号因不同感官而有质的不同;而相同感官输入的同质信号又因空间和时间的离散采样而有序位的不同，它们组成有标的数据集合.数据集合的标号提供感官的性质、感知的位置和时间、感知的方向等信息;数据集合中的序号则提供对同质信号所做的离散空间和离散时间的采样序位等信息;数据的取值为在一定的感觉精度之下的信号量化值.如果把一个人出生以来输入大脑的所有感知信号数据集合存为数据库，那就构成一个庞大的数据集团.这个数据集团就是该个人得以认知世界的全部的素材基础［4］.

1.2 认知信息加工的产品

这是一个外部客观世界反映在认知者脑海中的信息世界.由于世界所包含的信息量是如此庞大，一个人脑不可能全部容纳世界的所有信息［5］.因此，人脑中的世界信息是将外部世界加以简易化以后的信息.生物进化到人类，已经选择了一种极为优化的简易化的认知模式.将这种模式阐述如下:

1)大脑将世界的信息结构分为2部分:一部分是世界中实际情况的信息，另一部分则是世界中各种规律的信息.这2部分信息共同储存于大脑之中，构成大脑的全部知识——实况性知识和规律性知识.

2)大脑将世界的实况性信息分解为一个一个实物对象来加以认知.这是因为:一方面，实物是认知者在生活中所必须直接打交道的对象;另一方面，世界上实物的数量虽然无穷，但任何人只要选取其中与自己有关的一小部分(顶多上万个)去做认知也就够了，使认知对象大为简约;更为重要的一个方面，就是每个实物都具有一系列涵属于其自身的信息，认知一个实物就同时认知到其大量的有关信息，能起到“闻一知十”的认知效果.

3)每个实物的信息包括该实物是否存在，有什么属性，在各个时间点有什么状态(包括在何处，取何姿态，在做什么)等等，为认知者所关注的可以逐一列述的项目.其中，属性信息是基本不随时间变化的信息(至少是在一段时间中不变化的信息)，而状态信息则是随时间作变化的信息.

4)无论是属性信息还是状态信息，都有相应的标量或矢量的量化取值，这些取值的精度一般达到“认知适用”的要求即可.(有时，“认知适用”的取值只取在几种以至两种模式之中——这就是多元或二元信息，后者如动物生育属性只有胎生、卵生这两种模式取值，等等.)

1.3 实况性信息由不确定到清晰的加工

实际上实物的性态参数都是客观的存在，它们在某一时间点上的取值也应该是唯一的.但在准确认知以前，认知者对其取值常常不能确定，一般可以用在取值集上的概率分布函数来加以描述.

设某性态参数ρ，其“认知适用”的取值集为V，

在未准确认知时，ρ在V集合中可能取值的概率分布为

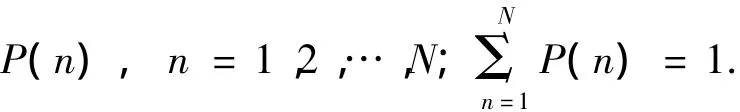
此时，对ρ值认知的不定度U为

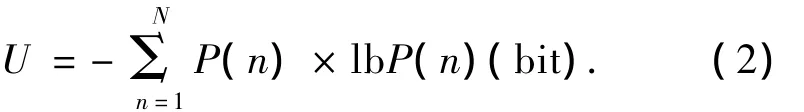
定义清晰度C:

可见，不定度U越大，清晰度C越低.

如已经获得事物某个性态方面的准确取值的信息，即消除了该信息的全部不确定性，此时该项信息的不定度U为零，或清晰度C为1(百分之百).

当一个实物全部需要认知的性态信息清晰度都为1时，就认为在“认知适用”意义上对该实物已完全了解.

1.4 加工后的世界实况性信息表现为数据文件集团

世界中“认知适用”的诸实物信息可以在脑中编列为一个一个的数据文件.其文件中应包含有该物的形象属性信息，还有若干用抽象概念和参数来表述的属性信息和状态经历信息.(就如一个人物的档案，应有他的照片——形象信息，还有若干条用取值来表述的他的主要属性和主要经历的概念性信息.)

当大脑调用一个实物的形象信息数据时，它可以将此数据用想象的心理机制产生出一个该实物的形象来;而且，还可以将此形象还原到它在外界的(与自己相对的)原有位置之上.

如果把世界中的诸实物的形象信息按照实物所在位置排列起来，加上在脑中已有的场景形象信息作为背景，人脑就可以把世界的总体形象想象出来(同时还能把各实物的概念信息联想到各实物之上).于是，在他脑中，就产生一个分布着诸实物的整体性的世界，一个他可以能动地在其中做应对行动以谋求生存的世界.

除了单个的实物而外，人脑还把若干实物组成集体(其中也包括实物系统)来加以认知.此外，还有“事”和“事件”，通常也和实物一样，被当做认知的对象.它们的信息同样也是实况性信息，也会在脑中被编列为一个一个的数据文件.

1.5 加工后的世界规律性信息也同样表现为数据文件集团

至于世界的规律性信息，它虽然不属于单个的实物(或实物集体)，但它反映若干实物(或实物集体)性态间互相制约的关系，它可以使大脑从一些已知的实况信息推测到另一些未知的实况信息，将脑中的信息世界极大地丰富起来.

规律性信息通常用概念性语句来表述，也可以用数学(或逻辑)的关系式来表述.这些表述可以是确定性的，也可以是概然性的.无论是语句还是公式本身都要用符号来进行编制，而符号必然会以相应的数据编码形式在脑中存在.因而，每个可以用符号来编程的反映规律的文件，其本身仍然是一个数据文件.调用此数据文件也就是应用此项规律.

1.6 认知的数学实质

人脑对于世界的全局性的认知，其实质就是将他有生以来感知信号的数据集团加工成他对世界认知的实况性信息和规律性信息的数据集团，是一种从数据集团到数据集团的庞大而复杂的数学变换.

这里所指的数学变换是广义的，不仅是数学解析式的(线性、非线性，等式、非等式)变换，也包括逻辑变换和程序转移指令等变换.当然，这种变换会比通信中所做的编码、译码变换复杂很多，这也就是大脑为什么有极其复杂的神经结构的原因.

2 认知信息变换的基本数学规律

然而，细细推究起来，从感知信号数据集团到世界信息数据集团之间的数学变换，仍然存在一种基本的数学规律，这个规律主宰认知活动的全过程.以下就来讨论这个基本的规律.

2.1 从感知信号中加工出“象”信息为一种减熵变换

世界信息中，无论是实物(实事)信息还是规律信息，都体现为一种数据约束 .如大部分实物都有一个基本不变的外部形状，这是由事物自身结构性的约束所造成.这个形状被认知者的眼睛看到，于是在其视觉信号中，就出现一个基本不变的图像，图像中的信号数据也会保持一种相对约束的关系.信息理论指出，在信号集合中所出现的任何数据约束，都在数学上体现为一种“减熵”(decrease in entropy，dH表示)，即信号不定度的减少.也就是说，客观事物的存在反映在感知信号集合之中会以一种“减熵”的形式表现出来.或者说，一旦认知者在所感知信号中检测到“减熵”，就意味着他观察到有事物存在以及该事物有何性态的信息.

如果在信号空间中的某个域上，检测到一个固定的互相约束的信号数据集合，且这个数据集合出现的概率远大于其在无序条件下可能出现的概率，则在信号空间中，认知者就观察到一个“象”.这个“象”可以是静态的图像，也可以是动态的图像;对于声音信号，则可能是一个雷声或人类语音;连续的运动、温度、压触等感觉信号也会产生出相应的“象”来.

在信号空间中出现“象”以后，可以赋予这个“象”以一个编码符号.显然，用“象”参与编码的信号数据集合的码量肯定有所压缩，因为“象”的出现就意味着“减熵”的出现.

设在Ω域上出现的象为“象A”，经计算，出现“象A”造成的减熵dHΩ为

式中:HΩ为未出现“象A”以前在Ω域上的无序信号的熵值，HΩ'为出现“象A”以后在Ω域上的熵值，PA为在Ω域上“象A”出现的概率，Hb(PA)为“象A”呈概率PA出现时所造成的不定度，函数Hb(P)为双码元的熵，当双码元的概率分别为P和1-P时，有

式中:各量单位为bit.

2.2 从诸多“象”信息中加工出“物”信息又是减熵变换

同一实物在长期被某认知者感知过程中，会多次以不同的“象”映射入其脑中的信号数据集团之内，大脑就会把这些“象”加以归纳整理，使之归属于同一个“物”，并赋予这个“物”以一个编码符号，这就是这个“实物”的名.还有，同一实物会有特定的声音(或体温等)时，大脑也会把这个声音(或体温等)的“象”赋予该实物.于是，把大量“象”(包括同质的和不同质的)看为同一实物的映象，从中处理出一个具有各种属性的实物的存在信息.这又是一次“减熵”的处理过程.

设象A1和象A2都是同一个物的映象(如面容中的眼睛和鼻子)，且均同时为认知者所观察到.因此，2个象的出现概率基本相同，设为共同的PA;

经计算，象A1的减熵为

象A2的减熵为

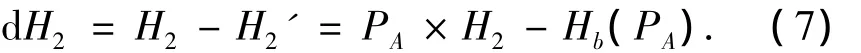
由于象A1和象A2均为同一物的映象，在同时出现，计算此种情况的减熵dH12为

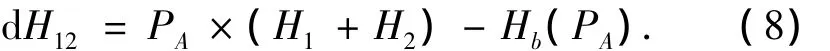
代入计算后:

即同属一物的两象的联合减熵值大于两象分别出现时的减熵值之和.

由此可见，当大脑把同一个物的所有各象赋予该物时，就会一次次地体现减熵.或者说，如大脑发现若干象信息在同时以特定的相对位置关系联合出现，并从而有明显的减熵时，大脑就认知到一个“物”.

从信号到“象”的减熵再从“象”到“物”(“事”)的减熵，这就是从信号数据集团中处理出关于世界事物(实况)信息数据集团的基本数学规律.

2.3 规律性知识的加工仍然是信息的减熵变换

至于规律性知识信息更是客观事物存在相互约束的反映.产生规律性信息也都是信息的减熵变换的结果.

2.3.1 事物分类规律

事物分类就表现为一种约束.有很大外延范围的同类物具有相同的本征属性，如“狗”类各物——即猪狗，都有四条腿、无角、有毛、嗅觉灵敏、行动快捷、为人类所豢养、忠于主人等等属性.这些同类物所具有相同的本征属性集合即在逻辑学中所称的内涵，就可以用同一个“概念”的编码符号来表示.在思维和语言中使用这种概念符号(语言或文字)就使编码量大为压缩.这当然也是＂减熵＂的结果.下面讨论一下这种减熵的计算.

将同类物O的本征属性作一个集合S，当S中各元素呈无序状态时有熵值HS;设同类物O在所有物中出现的概率为PO，则因同类物出现而使S中所呈现的熵值变为HS'，此时造成的减熵dHs应为

比较单个物和同类物，同类物内涵减少使HS减小，但外延加大又使PO加大，故减熵dHS是很显著的.

2.3.2 事物关联规律

事物关联也表现为一种约束.如有事件X和Y，在检测到2个事件联合出现的熵小于2个事件单独出现的熵值之和时，即有

这样的减熵表达式时，就发现2个事件存在关联，这就成为事物间概然性的或必然性的关联规律.

若发现

就说明2个事件是完全必然的关联.

此时，熵减量dH为

2.3.3 事物相似规律

事物性态相似也同样表现为约束［7］.很多物在静态的结构或很多事在动态的过程中存在相似性.这种相似性可以用一种减维变换来做运算而观察到.

在认知中，若广泛存在有众多不同类的物Om(m=1，2，…，M)，它们各具有相应的信息数据集合Dm，如果能找到一种减维数学变换J=T(D)(J为矢量，其维数远小于D的维数，但又必须大于零)，使

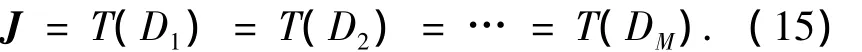
则称诸物(或诸事)之间存在相似性，J则为它们的相似中项.

认知到相似显然也是信息减熵.

2.3.4 科技理论

反映科学技术规律的现代科技理论，更是用严格的数学关系揭示了本学科参数之间的约束.一个式子就给出一种约束，排除了不符合该式子的一切可能.将科技规律作用于实物世界的信息集团之中，也必然使其熵(不定度)含量大为减少.

通常，科技工作者通过大量的观察实验，首先得到经验性的规律知识，再将若干经验性规律再做抽象性的归纳总结，就可以形成理论性的规律知识，理论知识甚至可以做成层叠的构架.

2.4 用减熵加工出的世界信息被极大地压缩了码量

把信号数据集团中的各个“象”检测出来，赋予它们以“象编码符号”;再将相关的“象”归纳为相应的“物”，赋予它们以“物编码符号”;然后，再寻找各物性态之间的联系，归纳为规律，赋予规律以“规律名符号”;从而最终建立起以这些概念符号即语言和文字为编码的整个世界事物信息档案即数据集团.可以肯定，凡是以代表大约束量的“象符号”、“物符号”、“规律名符号”等概念符号作为编码组成的信息数据集团，具有强大压缩编码量的效果.从而，在脑中“认知适用”的世界信息所占的码量也会尽可能地少.

这其实也就是为什么人类认知要使用“象”、“事物”及性态、“规律”等为词语即概念符号的语言体系的原因.

尽管各民族的语言不同，但从形象到概念的“简易化”的认知进化过程是基本相同的.所以只要经过词语的对译，不同语言的人们就可以迅速互相理解.进而言之，一个电脑机器人如果植入同样的简易化的认知软件，在其实践活动中，也就可以有仿人的智慧并能和人类进行概念性的思想交流.

虽然理论上说来，简易化认知所占的脑容量应该是最少，但大脑并不用Shannon最少码量原理来编码，而是用约束集合即＂概念＂为码元来编码.这是因为，用概念编码时，每个码元都具有一定的含义，大脑很快就对之理解，认知过程非常简捷清晰;而用最少码量原理来编码时，每个码元并无意义，必须连接一批码元到庞大的码本中去查译，这并不利于思维的活动.

3 Shannon信息理论和认知信息理论的对比

现在对比Shannon通信信息理论和认知信息理论在数学处理方面的不同之处:

1)通信理论在信源输入数据中寻找“约束”(即减熵)，为的是消除这些约束带来的冗余码量，因而在信源编码的数学变换中要消去这些约束;

而认知理论在感知输入数据中寻找“约束”，为的是发掘这些约束，使之成为事物信息的源泉，从而构建认知世界的信息体系.

2)通信理论研究的内容是:在信道容量有限的条件下，如何能保证有效地传输尽可能多的信源信息;

而认知理论研究的内容则是:在脑容量有限的条件下，如何有效地保证脑中的“认知适用”的信息世界具有最大的清晰度.

3)通信理论追求最小码量编码方法;

而认知理论中则使用“概念”来压缩编码，尽管已实现了很大的编码压缩，但并不是最小码量的编码.

4 从约束的变异中加工状态信息

那么，是不是在输入数据中只有“约束”才是认知所关注的内容呢?其实并不完全如此.前已提到，对世界信息的认知，除了事物的“存在与否”及其“属性如何”为重要的内容而外，事物的随时间变化的“状态如何”也是重要的内容.甚至在某种情况下，事物对象的当前状态对认知者具有生命攸关的重要意义.而状态信息的随时变化性质则表现为一种“变异”.但这种变异是联系于某个确定事物的变异;因事物体现约束，故状态变异是在约束基础上的一种变异.一般在大脑适时输入感知信号、检测约束即检测事物存在及其属性的同时，对事物参量的变异做出检测，确定此时的状态信息.

下面讨论从事物“象”信息的变异中加工出状态信息的数学原理.

假设某事物在大脑中已存储有一个象A，而在当前适时观察到的同一事物的象则为A';如存在有一种数学变换定式T(A，ρ)，其中ρ为一个标量或低维矢量(其维数远低于A的维数)，且有A=T(A，0).

当发现有

而ρ≠0时，则把ρ值看成为事物状态变化的参数值.

如果事物状态变化存在规律，ρ值常常是可以根据已经发生的实况信息和已知有关规律的运算加以预测.有时能准确地预测到，多数情况为预测值在很大程度上接近于实际观察之值.

如有某状态信息参数ρ，其“认知适用”的取值集为V，如式(1)所示.

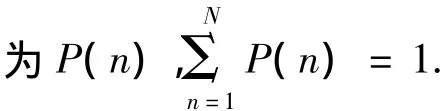
而在预测后，ρ在V集合中可能取值的概率分布变为

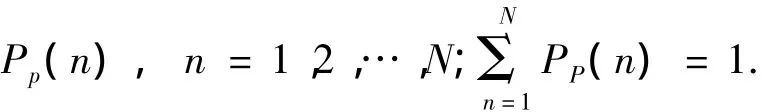
根据式(2)分别计算预测前和预测后的不定度之值为U和UP.

对于符合科学认知的预测，必有

即在预测时，将脑中的规律性知识作用于已知的实况性知识上，获得

的信息量.而在实际观察后，能准确测定ρ的取值时，认知者又进一步消除了UP所包含的全部不定度，使该信息的清晰度为1，即完全实现对该状态信息的认知.

预测方法在各种信号处理技术中都有应用.如线性预测编码——linear prediction coding在现代语音编码技术中就被广泛采用，即将出现的信号在预测后的平均不定度UP比起预测前的平均不定度U要明显减小.

实际认知中，大脑并非在所有信号数据全部取得以后再做加工，而是在每当有感知信号输入时，就立即在知觉的层级上进行快速而适时的分析计算，将有关的象信息和物信息提取出来，并根据需要指挥自身的行动;同时也会将重要的信息存入记忆;其余杂散的无序信号和无用信息则被基本清除，以节省大脑的存储空间［8］.然后，大脑再在思维的层级上，用归纳和演绎方法进行知识的推理活动，建立和丰富理论知识，用理论知识去指导自己的实践，并从实践的检验中不断修正和完善已有的知识体系.其间，大脑还要不断向他人、导师和书籍学习，这是大脑丰富其实况性知识和规律性知识的重要源泉.

5 结束语

认知信息论采用Shannon信息论中信息熵的数学概念，从输入信号数据集团中检测“减熵”以确定“象”信息;再联合诸个“象”信息用“减熵”法确定“物”(事)是否存在以及有什么样的属性的信息;同时，从所有事物性态的类比和关联中再寻找“减熵”以建立“规律”的知识信息;利用已知实况信息和规律知识去推测其他未知的实况信息，以及预测即将发生的事物状态;并在适时观察中，检测“象”的变异来确定事物当前的状态信息.这就是贯穿于“认知信息论”中的基本数学原理.

［1］SHANNON C E.A mathematical theory of communication［J］.The Bell System Technical Journal，1948，27:379-423，623-656.

［2］WIENER N.Cybernetics［M］.2nd ed.Cambridge:MIT Press，1961.

［3］HAKEN H.大脑工作原理［M］.上海:上海科技教育出版社，2000.

［4］LINDSAY P H，NORMAN D A.人的信息加工［M］.北京:科学出版社，1987.

［5］黄秉宪.脑的高级功能与神经网络［M］.北京:科学出版社，2000.

［6］ASHBY W R.An introduction to cybernetics［M］.London:Chapman＆ Hall Ltd，1956.

［7］钱学森.关于思维科学［M］.上海:上海人民出版社，1986.

［8］SOLSO R L，KIMBERLY MACLIN M，MACLIN O.Cognitive Psychology［M］.Beijing:Beijing University Press，2004.