OFDM系统用户上行有效吞吐量最大化算法

潘科，左勇，刘学勇，陈杰

(中国科学院微电子研究所通信与多媒体SoC研究室，北京100029)

近年来，为了提高频谱利用效率，正交频分(orthogonal frequency division multiple，OFDM)通信系统中的子载波和功率自适应分配问题得到了广泛研究.根据优化目标的不同，该研究方向主要包括两类问题:裕量自适应(margin adaptation，MA)问题和速率自适应(rate adaptation，RA)问题.MA问题主要是研究在用户固定传输速率和误码率约束条件下，最小化发射总功率;RA问题主要是研究在系统发射总功率约束条件下，最大化系统吞吐量.除了发射总功率的约束，RA问题又按照其余不同的约束条件，主要分为3类:1)在误码率约束下，速率最大化(rate maximization，RM)［1-2］;2)在速率约束下，误码率最小化(BER minimization，BM)［3-4］;3)有效吞吐量最大化(goodput maximization，GM)，有效吞吐量是指接收端在单位时间内正确接收到的数据量.其中前两类问题，主要是针对语音和视频传输等实时性业务，有固定的误码率要求或速率要求.第3类问题与前两者不同，它主要针对文件传输和网页浏览等非实时性业务.这类业务往往既没有固定的误码率要求，又没有固定的速率要求，但要求接收的数据完全正确.在发送端，上层的数据被打包传输;接收端对数据包进行循环冗余校验(cyclical redundance checking，CRC)，只要数据包中有错误比特，整个数据包就被丢弃，因此有效吞吐量是此类业务最重要的性能参数.

以往对资源分配的研究集中于MA、RM和BM问题，对于GM问题的研究多限于解决一个OFDM符号上的子载波分配问题，而对时间和频率资源，即OFDM符号和子载波，同时进行分配的研究很少.Devillers等［5］研究了基于GM的功率和子载波分配问题，得出子载波等误码率的功率分配方式是一种接近最优的功率分配方式的结论，但所提出的算法只适用于一个OFDM符号上的子载波分配.Stupia等［6-7］虽然把GM问题的研究扩展到了多输入多输出(multiple input multiple output，MIMO)系统，但提出的算法仍然没有考虑二维的时频资源.另一方面，文献［8-10］虽然研究了基于GM的包长优化问题，但没有结合OFDM系统用户上行GM的特点.

本文针对OFDM系统用户上行GM问题的特点，提出了一种新的用户上行资源分配策略，通过分步求解数据包长度和数据占用的子载波数的联合优化问题，并提出了一种用户上行有效吞吐量最大化算法，取得了较传统算法更高的有效吞吐量.

1 OFDM系统上行链路模型

采用时分双工的多用户OFDM系统中，多个连续的OFDM符号组成一帧，一帧分为上行子帧和下行子帧，在一帧内信道状态假定是不变的.资源分配每一帧做一次，分为上行资源分配和下行资源分配.

上行链路的资源分配过程分为两个方面.以802.16d系统［11］为例，一方面，基站端在下行子帧开始之前，以用户为单位进行多用户间的系统资源分配，用户资源分配信息在下行子帧中传输给用户端.另一方面，单个用户端在收到资源分配信息后，得知基站为其分配的上行资源，在上行子帧开始之前为其各种业务进行资源分配，本文将此种资源分配称为用户上行资源分配(user-uplink resource allocation，UURA).

本文不考虑基站端多用户间的系统资源分配问题，只研究单个用户端的UURA问题，问题的目标是使用户上行有效吞吐量最大化(user-uplink GM，UUGM).

假设用户分得的子载波数为N，带宽小于信道相干带宽，该用户各子载波的信道增益近似相等;分得的OFDM符号数为M;在用户端，精确的信道状态信息已知.OFDM系统的上行链路模型如图1所示，其中用户端的选择性自动重传(selective repeat-ARQ，SR-ARQ)模块处理基站端校验数据包后反馈的确认(ACK)或重传(NACK)请求，实现数据包的重传.系统子载波总数为Nsys.系统可使用 QPSK、16QAM和64QAM这3种调制方式.

OFDM系统中用户上行时频资源平面如图2所示.用户可用的资源包括N个子载波和M个OFDM符号，资源的基本单位为资源槽(slot，它由一个子载波和一个OFDM符号组成.若一个数据包占用n个子载波和m个OFDM符号，则占用mn个slot.

图1 OFDM系统上行链路模型Fig.1 The uplink model of the OFDM system

图2 OFDM系统用户上行时频资源平面Fig.2 The user-uplink time-frequency resource plate of the OFDM system

2 用户上行资源分配策略分析

OFDM系统的UUGM问题有2个特点:1)若给定用户的发射功率，则每个子载波上的接收信噪比与用户数据占用的子载波数成反比;2)数据包长度，即数据包占用的资源数，与数据包占用的OFDM符号数成正比.

传统包长优化算法［8-10］中有效吞吐量表达式为

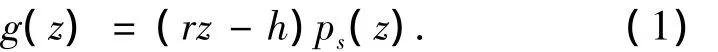
式中:z为数据包的长度，ps为数据包成功传输的概率，r是在给定的某调制方式下每个子载波上承载的比特数，h为数据包的信令消耗.由于式(1)中只有一个变量，没有体现OFDM系统中UUGM问题的特点，所以传统包长优化算法不能很好地适用于该问题.

Devillers等［5］给出的有效吞吐量表式为波数集合为V={ni|i=1，2，…，NP}，成功传输的概率集合为W={Pri|i=1，2，…，NP}，则 OFDM 系统的用户上行有效吞吐量可表示为

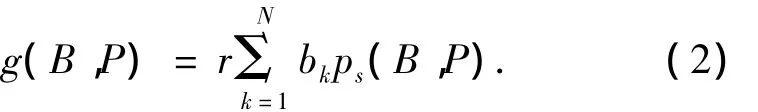
式中:bk表示子载波k上的比特数，B={bk|k=1，2，…，N}，P为各子载波上的功率组成的集合.式(2)虽然通过控制子载波上的比特数和功率可以控制用户数据占用的子载波数，但子载波分段数和OFDM符号数都被限定为1，从而限制了有效吞吐量的最大化.

本文针对OFDM系统UUGM问题的特点，提出了一种新的用户上行资源分配策略.该策略通过优化配置数据包占用的子载波数、OFDM符号数和子载波分段数，可使得有效吞吐量最大化.

假设数据包在用户时频资源平面上占用的资源块为矩形;ni、mi分别为数据包i占用的子载波数和OFDM符号数;Pri为数据包i成功传输的概率，它受数据包i的长度和每个子载波上的接收信噪比影响;NP为数据包总数.设各数据包占用的OFDM符号数集合为U={mi|i=1，2，…，NP}，占用的子载

由文献［5］可知，使同一数据包各子载波上的误码率相等是一种接近最优的功率分配方式，因此本文的功率分配采用该方式.又因为假定用户带宽小于信道相干带宽，用户每个子载波上的信道增益近似相等，所以同一数据包每个子载波上的发射功率近似相等，数据包i的误码率BERi可表示为［12］

式中:B为系统带宽，N0为零均值高斯白噪声的单边功率谱密度，g为每个子载波的信道增益，pi和SNRi分别为数据包i的发射功率和接收信噪比，c1=0.5，c2=1.5，Pri表示为

为便于分析，假设所有数据包占用的子载波数相同，OFDM符号数相同，即mi=mj=m，ni=nj=n，i=j，m和n分别为数据包OFDM符号数和子载波数;所有数据包的发射功率相同，即Pi=P/t，P为用户的发射总功率，在上行链路方向，用户的发射功率是资源分配的一个关键约束条件，t为子载波分段数.如果用户时频资源平面的频率轴方向上排列着t个数据包，那么子载波分段数为t.

将m、n、t以及式(4)、(5)代入式(3)得到新策略下有效吞吐量的表达式为

式中:M/m表示OFDM符号分段数w，说明用户时频资源平面的时间轴方向上排列着w个数据包.可知，用户分得的M个OFDM符号在新策略中将全部被用于数据传输.

将式(6)与式(1)、(2)比较可知，新策略全面地考虑了OFDM系统UUGM问题的2个特点，每个子载波上的接收信噪比与用户数据占用的子载波数nt成反比，而数据包的包长是m与n的乘积，它不但与n有关，还与m有关.

3 用户上行有效吞吐量最大化算法

3.1 UUGM问题及其分解

3.1.1 原始问题

由表示有效吞吐量的式(6)可知，数据包占用的子载波数n越大，传输的数据量越大，但每个子载波上的信噪比越低;数据包的OFDM符号数m越大，信令消耗占数据总量的比例越小，但数据包成功传输的概率越低;子载波分段数t越多，传输的数据包越多，但数据包成功传输的概率越低.因此，要使得有效吞吐量最大，就必须优化配置m、n、t.

新策略下的UUGM问题可表示为

该问题属于非线性整数混合规划问题，枚举法可求得最优解，它的复杂度为

3.1.2 原始问题的分解

为得到一种低复杂度的算法，将复杂的原始问题分解成2个较简单的子问题，即用户有效资源分配问题和数据包参数设置问题.

用户有效资源分配问题，主要研究如何合理设置用户有效资源参数，使得用户上行有效吞吐量最大化.由式(7)和(8)可知，n和t相互独立，要求nt≤N，所以用户分得的N个子载波可能只有部分被用于数据传输，即用户分得的资源并不都是有效的，只有用于传输用户数据的部分才是有效的，剩余的部分是无效的.用户有效资源的参数包括数据包的包长l和用户数据占用的子载波数x，其中l=mn，x=nt.将l和x代入式(7)，变量的个数将从3个减少到2个，得到用户有效资源分配问题的表达式:

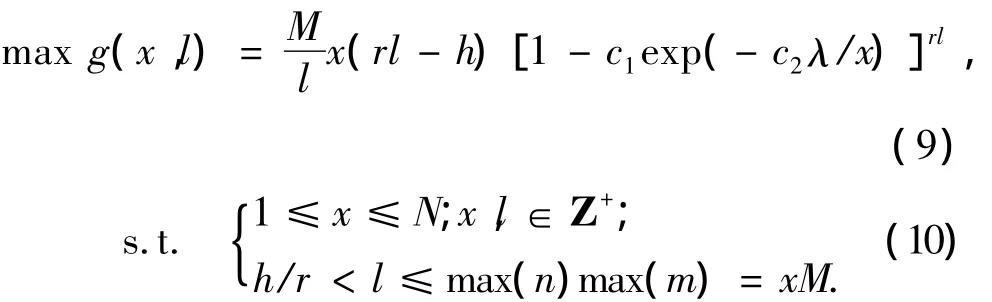
式(10)说明用户数据占用的子载波数必须小于用户可用的子载波数，要使得有效吞吐量为正值，包长必须大于信令消耗占用的资源量，而且必须不大于用户数据占用的总资源量.

数据包参数设置问题，主要研究如何合理设置数据包的参数，使得实际的有效吞吐量尽量接近用户有效吞吐量最大值.如果得到了x和l的最优解，那么只要找到m，n，t∈Z+使得l=mn，x=nt成立，则m、n和t就是原始问题的最优解.但是，这样的m、n和t很难找到，所以g(x，l)的最大值是g(m，n，t)最大值的上界，这里希望后者能尽量接近前者.又因为g(x，l)是x和l的连续函数，所以这里希望mn与l的差距和nt与x的差距都尽量小，从而使得g(m，n，t)与g(x，l)的差距尽量小.于是，数据包参数设置问题的表达式:

3.2 用户有效资源分配问题分析

单调性特征描述了函数在定义域不同区间上的单调性，它包括单调递增、单调递减、单峰、单谷和先峰后谷.单峰是指函数有且只有一个极大值点;单谷是指函数有且只有一个极小值点;先峰后谷是指函数有且只有2个极值点，其中一个为极大值点，另一个为极小值，而且极大值点的x轴坐标小于极小值点的x轴坐标.

3.2.1 目标函数单调性特征分析

为便于分析，这里放宽x、l为整数的约束条件，令x，l∈R+，并把g(x，l)分为两部分:

当x给定时，要使得f2(x，l)最大，l的最优解可以表示为［8］

定理1 存在唯一的x*∈(h/(rM)，+∞)，使得下式成立:

证明 设l1(x)=Mx，其定义域为(h/(rM)，+∞)，l1(x)在定义域上单调递增，可得

设l2(x)=L(x)，当x∈(h/(rM)，+∞)时l2(x)单调递减，可得

所以l1(h/(rM))-l2(h/(rM))＜0，l1(+∞)-l2(+∞)＞0，且l1(x)和l2(x)都为连续函数，故必然存在的x*∈(h/(rM)，+∞)使得l1(x*)=l2(x*).由l1(x)和l2(x)单调性可知x*唯一，而且由约束式(12)可知，当x＜x*时，l2(x)＞l1(x)，l(x)=l1(x);当x＜x*时，l1(x)＞l2(x)，l(x)=l2(x).因此命题得证.

由定理1可知，l(x)是(h/(rM)，+∞)上的分段函数，因而f2(x，l)和g(x，l)也是x的分段函数.把式(15)代入g(x，l)得

式中:

引理1 当x∈(h/(rM)，+∞)时，g1(x)是x的单峰函数.

证明 将式(12)和(17)代入式(16)可得

由于g1(x)＞0，所以g1(x)和lng1(x)的单调性相同.令y(x)=lng1(x)，对y(x)求导可知:

由于y'(x)连续，所以存在h/(rM)＜＜+∞，使得y')=0.对y(x)求二阶导可知y″(x)＜0，即y'(x)单调下降.所以，当h/(rM)＜x＜+∞时，y'(x)有且只有一个零点，y(x)有且只有一个驻点，等价于g1(x)有且只有一个驻点.又因为g1(x)连续，有

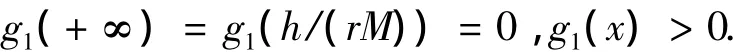
所以，当x∈(h/(rM)，+∞)时，g1(x)有且只有一个最大点，是x的单峰函数，命题得证.

引理2g2(x)和'(x)的单调性特征与λ无关.

证明 令 λ 分别等于 λ1和 λ2，其中 λ1=αλ2，且 α∈R+，α ≠1，令

因为对于任意x1必然存在x2=x1/α，使得

所以g2(x，λ =λ1)与g2(x，λ =λ2)一一对应，极值点个数相同.因为α＞0，所以g2(x，λ=λ1)与g2(x，λ=λ2)的单调性特征相同.又因为 λ1和 λ2是任意取值，所以g2(x)的单调性特征与λ无关，λ的变化只是对g2(x)函数曲线的压缩或拉伸.

引理3 当h=1，2，…，2 048且x∈(0，+∞)时，g2(x)有且只有一个极大值点和一个极小值点.如果令极大值点和极小值点的x轴坐标分别为x1和x2，那么x1＜x2.

证明 根据式(16)可知，g2(x)的单调性特征只与参数λ和h有关，而引理2已证明g2(x)的单调性特征与λ无关.所以当h=1，2，…，2 048，即为有限的离散值时，假定λ为常数，将h逐一代入g2(x)检验命题的真假.因为g2'(+∞)=d，d是大于0的常数，所以在x较大时g2(x)单调递增，在检验时x不必取到无穷.所有检验结果均表明了g2(x)在(0，+∞)上有且只有一个极大值点和一个极小值点，且x1＜x2.因此，命题得证，g2(x)是先峰后谷函数.

引理3中h是每个数据包的信令消耗量，实际系统中该消耗量为常数，这里假设该常数的取值范围为从1到2 048的整数.

g(x)是由g1(x)和g2(x)组成的两段函数，它的单调性特征由下面的定理2可知.

定理2 当h=1，2，…，2 048且x∈(h/(rM)，+∞)时，g(x)是先峰后谷函数或者单峰函数或者单调增函数.

证明 设g1(x)的极大值点、g2(x)的极大值点和极小值点以及g(x)的分段点的x轴坐标分别为、x1、x2、x*.由定理1可知x*＞h/(rM)，由引理1可知＞h/(rM).因为g(x)是由g1(x)和g2(x)所组成的分段函数，g1(x)和g2(x)的单调性特征已知，所以g(x)的单调特征容易得到.g(x)的单调性特征如表1所示，表中a和b分别代表当x＜x*和x＞x*时g(x)的单调性特征.

表1 g(x)的分段单调性特征Table 1 The sectional monotonicity of function g(x)

表1中有2种情况并未讨论.因为L(x)为l(x)的最佳取值，所以当x∈(h/(rM)，+∞)时，g2(x)≥g1(x).假设g1(x)＞g1(x*);假设时，，得到矛盾，因此，的情况不会出现.同理可证，的情况也不会出现.

由表 1易得:当h=1，2，…，2 048且当x∈(h/(rM)，+∞)时，g(x)只能是先峰后谷函数或者单峰函数或者单调增函数.因此，命题得证.

3.2.2 L 搜索算法

定理2中，x定义域为(h/(rM)，+∞)，而考虑式(10)，则x的 定 义 域 为 ［max(1，ceil(h/(rM)))，N］，ceil(x)表示不小于x的最小整数.因而，式(9)中g(x)的单调性特征是定理2中g(x)部分定义域区间上的单调性特征.因此g(x)在式(9)定义域上的单调性特征有以下5种可能:单调递增、单调递减、单峰、单谷和先峰后谷.

单调函数和单谷函数的最大值一定都在定义域区间的端点处，只需比较端点处的函数值即可.因为x∈Z+，所以运用二分法就可以准确搜索得到单峰函数的极大值点坐标.然而，由于先峰后谷函数的定义域中存在两段单调上升的区间，通过斜率值的符号无法判断二分点的x轴坐标是否大于极大值点的x轴坐标，所以先峰后谷函数的极大值点坐标无法直接运用经典的二分法得到.

定理3 当h=40，41，…，2 048时，设x1和x2分别为g2(x)的极大值点和极小值点的x轴坐标，那么'(x)是单谷函数，且存在唯一的极小值点，其x轴坐标为，使得

图3 L搜索算法流程Fig.3 The flow chart of L search algorithm

3.3 数据包参数设置问题分析

由式(11)可知，数据包参数设置问题为整数非线性混合规划问题，如果用枚举法逐一搜索3个变量，其复杂度为O(MN·lnN).为了降低复杂度，提出了一种次优的M搜索算法，该算法只搜索每包OFDM符号数这一个变量，其复杂度为O(M).

一方面，为了使(x-nt)2最小，本文放宽了对t为整数的约束，使t取实数.其中对于任意整数x和n，t=x/n;当t为非整数时，t=ti+tf，ti为t的整数部分，tf为t的分数部分.x个子载波被相应地分为两部分:1)nti个子载波，2)剩下的(x-nti)个子载波，打包时两部分将分别处理.

另一方面，由于t=x/n，式(11)等价于min|lmn|.为了使|l-mn|最小，逐一搜索m，对应的n由l/m四舍五入得到.因为l/m=n≤max(n)=x，所以m的搜索范围是l/x≤m≤M.如果m是M的因子，在同等条件下将被优先选择.当w=M/m非整数时，w=wi+wf，wi为w的整数部分，wf为w的分数部分.M个OFDM符号被相应地分为两部分:1)mwi个OFDM符号，2)剩下的(M-mwi)个OFDM符号，打包时两部分将分别处理.因为子载波与OFDM符号都分别被分为了两部分，所以组合起来有4种类型的数据包，如表2所示.如果出现包长小于h/r的情况，则不给该类型的包填充数据.

表2 数据包类型参数Table 2 Parameters of data packet

M算法的流程如图4所示.其中，m|M表示m整除M，rd(x)表示对x四舍五入，mopt、nopt、topt分别是算法得到的数据包的OFDM符号数、子载波数及子载波分段数.

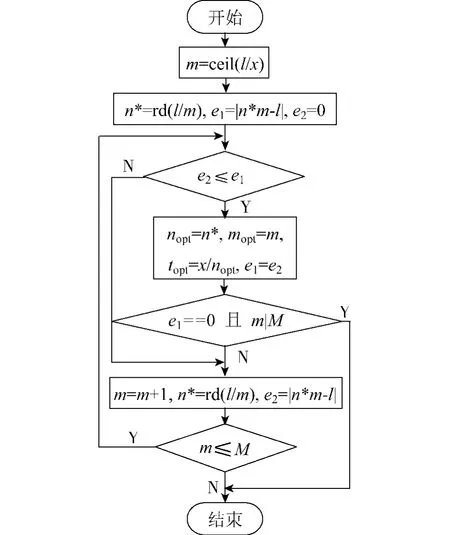
图4 M搜索算法流程Fig.4 The flow chart of the M search algorithm

3.4 UUGM算法及其复杂度分析

结合L和M搜索算法，本节提出了一种用户上行有效吞吐量最大化算法UUGM.该算法的流程如图5所示，其中，J表示调制方式的种类数，j表示第j种调制方式，gmax表示最大有效吞吐量.由3.2节可知，L搜索算法的复杂度与二分法的复杂度相同，为O(lnN)，由3.3节可知M搜索算法的复杂度为O(M).UUGM算法先调用L搜索算法，再调用M搜索算法，所以它的复杂度为O(lnN+M).

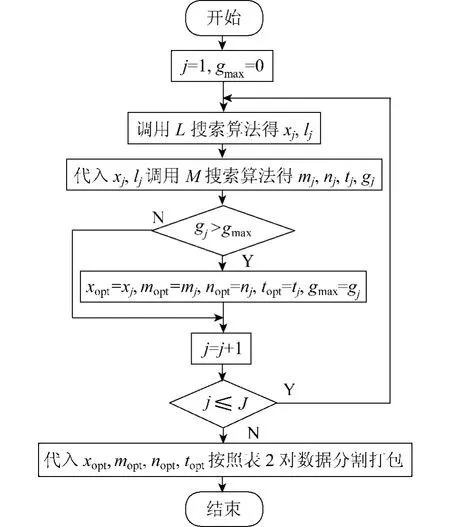
图5UUGM算法流程Fig.5 The flow chart of the UUGM algorithm

已有算法(如传统策略下的包长优化算法(GB_CLASSIC)［8］、M_OFDM_TDMA 算法［5-7］和 OFDMTDMA非优化算法)的复杂度如表3所示.其中，GB_CLASSIC算法的每个数据包占用的子载波数固定为N，OFDM符号数可由解析表达式求得，复杂度为O(1).M_OFDM_TDMA算法是文献［5-7］的算法在用户带宽小于相干情况下的等效算法，每个数据包占用的OFDM符号数固定为1，子载波数为自适应控制变量，复杂度为O(lnN).OFDM-TDMA非优化算法中，每个数据包占用的子载波数为N，符号数为1.

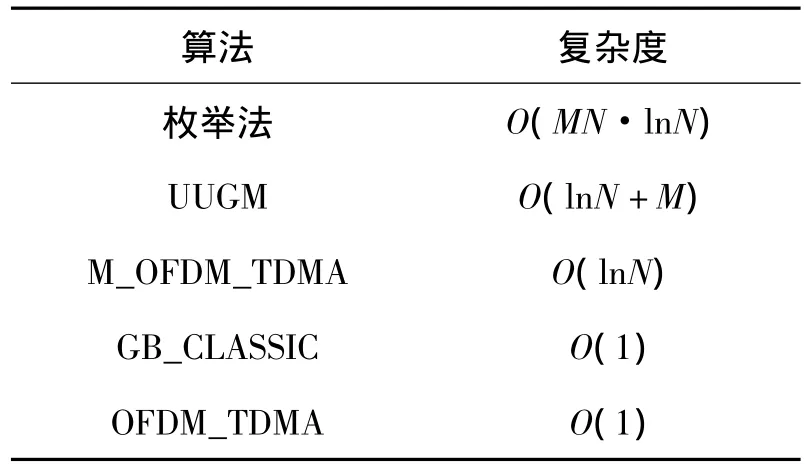
表3 算法复杂度比较Table 3 Computational complexity of algorithms

从表3可见，GB_CLASSIC和OFDM_TDMA算法复杂度最低，但从后面的仿真结果得到，它们的有效吞吐量也是最低的.而UUGM算法的复杂度虽然略高于M_OFDM_TDMA算法(M通常远小于N)，但远低于枚举法.

4 仿真结果分析

通过仿真将UUGM算法的性能与枚举法和已有的基于GM的算法进行了比较.仿真系统参数为Nsys=1 024，N=128，M=20，h=64，用户带宽小于相干带宽，信道增益服从瑞利分布.用户的有效吞吐量值为传输1 000帧后得到的平均值.

UUGM算法与枚举法的有效吞吐量如图6所示.可见，UUGM算法的有效吞吐量接近于枚举法(EX).图7为UUGM算法与已有算法的有效吞吐量比较.

图6 UUGM算法和枚举法的有效吞吐量Fig.6 The goodput of the UUGM algorithm and the enumeration method

图7 4种算法下的用户有效吞吐量Fig.7 The user goodput of 4 algorithms

由图7可见，4种算法当中，OFDM-TDMA算法由于未进行任何优化，有效吞吐量最低.GB_CLASSIC算法虽然复杂度较低，但有效吞吐量较低.M_OFDM_TDMA算法与UUGM算法复杂度相当，有效吞吐量相对较低.相比之下，新策略下UUGM算法的有效吞吐量明显高于其他3种算法.例如当平均信噪比为0 dB时，UUGM算法的有效吞吐量为278.1 bit/帧，而其余3种算法中最大的有效吞吐量为97.19 bit/帧，前者比后者高出了186%;当平均信噪比15 dB时，UUGM算法的有效吞吐量比其余3种算法中的最大有效吞吐量高出了5%.

5 结束语

提出的用户上行有效性吞吐量最大化算法UUGM，以少量提升计算复杂度为代价，较传统算法明显地提高了有效吞吐量.本文对信道近似平坦的假设是基于单个用户的上行带宽较窄情况，而频率选择性信道下的有效吞吐量优化问题将有待进一步研究.

［1］BASHAR S，DING Z.Admission control and resource allocation in a heterogeneous OFDMA wireless network［J］.IEEE Trans on Wireless Communications，2009，8(8):4200-4210.

［2］KO H，OH S，KIM B，et al.Simple bit allocation algorithms with BER-constraint for OFDM-based systems［C］//WCNC09.Budapest，Hungary，2009:1-5.

［3］ERMOLOVA N Y，MAKAREVITCH B.Low complexity adaptive power and subcarrier allocation for OFDMA［J］.IEEE Trans on Wireless Communications，2007，6(2):433-437.

［4］ERMOLOVA N Y，MAKAREVITCH B.Performance of practical subcarrier allocation schemes for OFDMA［C］//PIMRC07.Hilten Athens，Greece，2007:1-4.

［5］DEVILLERS B，LOUVEAUX J，VANDENDORPE L.Bit and power allocation for goodput optimization in coded parallel subchannels with ARQ［J］.IEEE Trans on Signal Processing，2008，56(8):3652-3661.

［6］STUPIA I，VANDENDORPE L，LOUVEAUX J，et al.Power allocation for goodput optimization in BICM-OFDM systems［C］//ICC08.Beijing ，China，2008:3604-3608.

［7］STUPIA I，GIANNETTI F，LOTTICI V，et al.BICMBOFDM link resource adaptation［C］//ICC09.Dresden，Germany，2009:1-5.

［8］MODIANO E.An adaptive algorithm for optimizing the packet size used in wireless ARQ protocols［J］.Wireless Networks，1999(5):279-286.

［9］CICCARESE G，BLASI M D，MARRA P，et al.A packet size control algorithm for IEEE 802.16e［C］//WCNC08.Las Vegas，USA，2008:1420-1425.

［10］ZHANG Y，SHU F.Packet size optimization for goodput and energy efficiency enhancement in slotted IEEE 802.15.4 networks［C］//WCNC09.Budapest，Hungary，2009:1-6.

［11］IEEE.IEEE Std 802.16d，IEEE standard for local and metropolitan area networks—part 16:air interface for fixed broadband wireless access systems［S］.Hoboken:IEEE，2004.

［12］GOLDSMITH A J，CHUA S.Variable-rate variable-power MQAM for fading channels［J］.IEEE Trans on Communications，1997，45(10):1218-1230.