基于EMD和HHT的航空发动机转子－机匣振动信号分析

徐可君，秦海勤，江龙平

(海军航空工程学院 青岛分院航空机械系，青岛 266041)

由于结构形式和现实安装条件的限制，航空发动机的振动信号通过机匣拾取。而机匣振动信号是转子系统所激振动经过多层结构传递以及与系统内其他激振源所激振动相互调制后的综合反映，加之机匣质量分布和各部分连接刚性的不同使得转子－机匣系统的振动信号一方面呈现出强烈的非线性和非平稳性［1，2］，另一方面振动信号经过多层结构的传递后部分故障信息衰减较为严重。因此基于传统的线性理论对航空发动机实测振动信号进行分析难以有效提取故障信息，受到了限制。

经验模态分解法(Empirical Mode Decomposition，EMD)是近年来提出的一种针对非线性和非平稳信号处理的新方法，是对传统的以傅里叶变换为基础的线性稳态谱分析的一大突破［3－7］。EMD基于信号自身的局部特征时间尺度，把原始信号分解为若干内在固有模态函数(IMF)，而不是像傅里叶变换把信号分解成正、余弦函数。它是自适应的，非常适合处理非线性和非平稳信号。

本文将EMD和HHT方法引入航空发动机转子－机匣系统的振动信号分析，某台发动机的台架实测机匣振动信号的分析结果表明，该方法具有较高的故障诊断精度，并较好地再现了高压压气机转静系统碰摩故障的演变过程。

1 EMD和HHT基本原理

EMD方法假设任何信号都是由基本信号——IMF组成，即若干个IMF相互叠加便形成复杂的复合信号。每一固有模态函数表示信号的一个内在特征振动形式，它满足以下两个条件:① 整个信号中，极值点数和过零点数相等或至多相差一个;② 在任意点，由局部极大值点和局部极小值点分别确定的上、下包络线均值为零，即信号关于时间轴局部对称。

对于任意时间序列x(t)经过经验模态分解后得到一系列固有模态函数 c1，c2，…，cn和一个剩余分量，如下表示为:

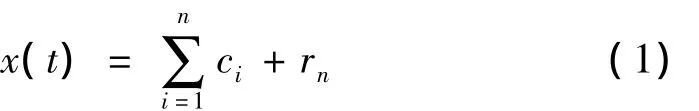
经验模态分解后的各IMF是单组分的信号分量。对c1，c2，…，cn分别进行Hilbert变换得到与其相对应的解析信号:

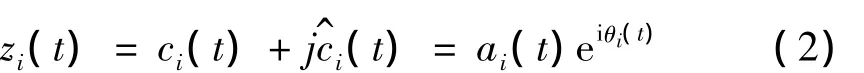
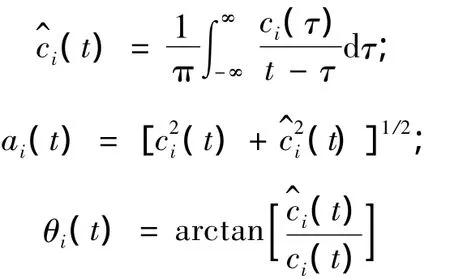
定义瞬时频率为:

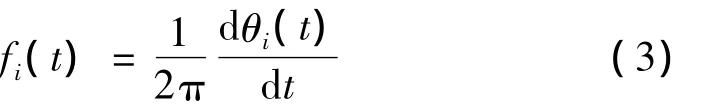
则原始数据可进一步表示为:

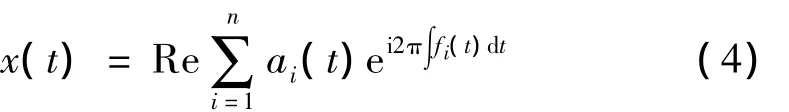
这里忽略了剩余分量rn，因为rn通常为单调函数或者值很小，Re表示取实部。定义式(4)右边为Hilbert谱:

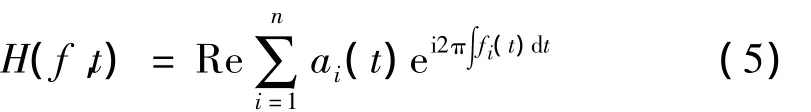
H(f，t)对时间t积分则得边际谱为:

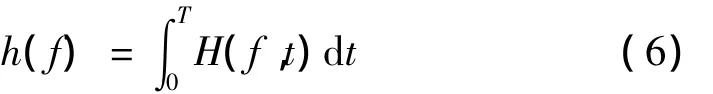
其中T为信号的时间长度。

上述过程即为希尔伯特－黄变换(Hilbert-Huang Transform，HHT)。

相同信号x(t)的傅里叶展开式为:

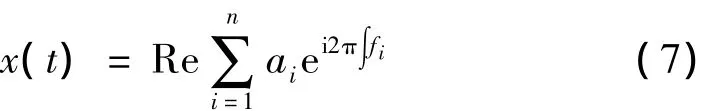
其中ai，fi为常数。比较式(4)和式(7)可看出，HHT对信号的瞬时频率表示是傅里叶展开的一般化，它不但提高了信号表示的效率，而且可表示变化的频率，突破了傅里叶变换的束缚。傅里叶频谱中某一点频率上的幅值表示在整个信号中有一个含有此频率的正弦或余弦函数组分。而H(f，t)或h(f)中有某一频率的能量出现时只表示该分量在某一局部出现过，它既可在其他局部消失也可在其他局部继续存在。这正是边际谱与傅里叶谱的本质区别，也是边际谱的优越性。

2 航空发动机转子－机匣振动信号分析

为了验证EMD和HHT对振动信号分析的有效性，对某型航空发动机的台架实测机匣振动信号进行了验证分析。

该型航空发动机在台架测试时安装有三个测振点，分为前测点、中测点和后测点。其中前测点位于低压压气机机匣前安装边右侧;中测点位于安装在扩散机匣上的点火燃油喷嘴支架上部;后测点通过低压涡轮轴承座振动传感器组件安装在7号轴承支座的下部。

三个测振点能够比较客观真实地反映该型发动机的振动情况，但又各有所侧重。前测点主要反映低压压气机的振动;中测点综合反映发动机高低压转子的振动，但对高压转子的振动更敏感;后测点主要反映低压涡轮的振动，一定程度反映高压转子的振动［9］。

发动机在台架测试按正常程序加速过程中，当高压转速上升至9606 r/min(76%NH)左右时中测点振动突然增大，继续升速，振动有所减小。当高压转速升至12134 r/min(96%NH)左右时，中测点振动超限报警。在下降过程中，当高压转速降至8216 r/min(65%NH)左右时，中、后测点振动同时增大，中测点的增幅尤为显著。前测点在此过程中一直在正常范围内。

为了分析振动增大和振动超限报警的具体原因，在这三个转速附近对中测点和后测点分别测取了若干稳态下的振动信号。每次采集按整周期采样，每周期采集128个点，采集了16个周期，共2048个点。

图1和图2为利用EMD和HHT对增速过程中高压转速为9930 r/min(78.5%NH)时中、后测点的振动信号分析结果。

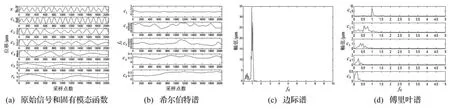
图1 增速过程中78.5%高压转速下中测点信号分析结果Fig.1 The results for middle measuring signal at the speed of 78.5%NH in the acceleration process

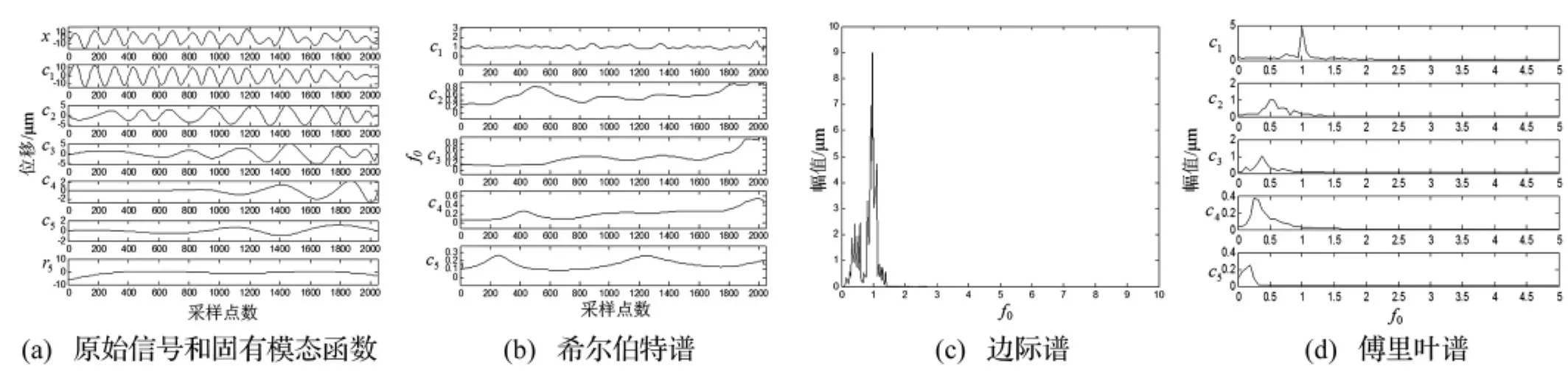
图2 增速过程中78.5%高压转速下后测点信号分析结果Fig2 The results for rear measuring signal at the speed of 78.5%NH in the acceleration process

图3 增速过程中90%高压转速下前测点信号分析结果Fig3 The results for middle measuring signal at the speed of 90%NH in the acceleration process

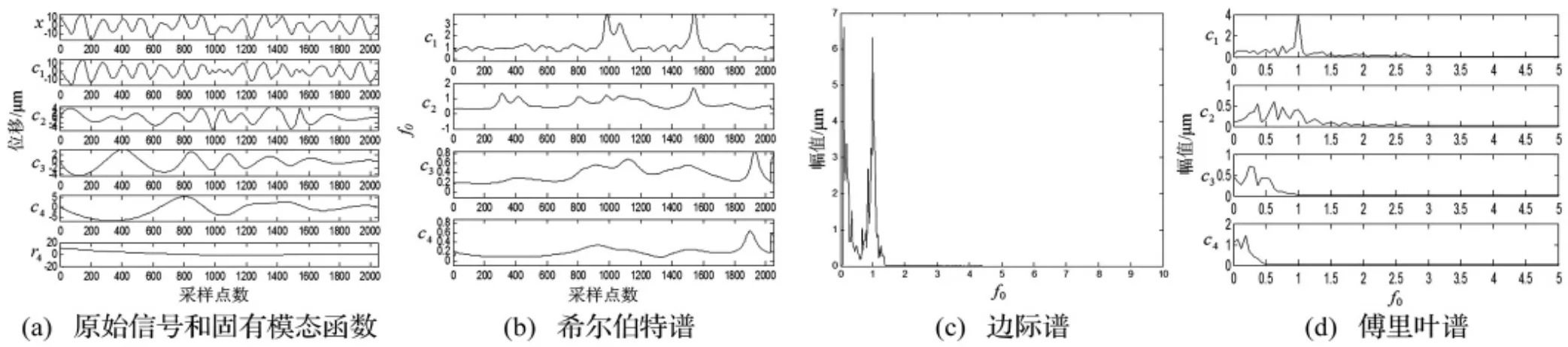
图4 增速过程中90%高压转速下后测点信号分析结果Fig4 The results for rear measuring signal at the speed of 90%NH in the acceleration process

分析图1和图2可得，利用EMD把原始信号分解成了5阶IMF和一个剩余分量。分析图1(b)和图2(b)可看出，第一阶IMF对应系统的工频，第二阶到第五阶IMF对应系统的低倍频分量。工频分量贯穿整个采样周期，而其他各阶IMF对应的低倍频分量在整个采样周期中是时变的。后测点的低倍频分量随采样周期的增加稍有波动，但总体上频率呈上升趋势。中测点的低倍频分量采样过程中频率波动较大，并随阶次的提高趋于平稳。这不仅说明了系统运行时发动机各部件激起的低倍频分量相互调制使得振动复杂化，而且进一步证明了发动机机匣的振动信号是非平稳非线性的。对比图1(d)和图2(d)可知，虽然传统的傅里叶变化产生的连续谱值也表明机匣的振动信号是非线性的，但对于频率随采样周期的变化以及频率的局部信息等却无从知晓。

分析图1(c)和图2(c)的边际谱可知，工频分量明显占优，尤其是中测点的工频分量非常明显。结合中测点的安装部位对于高压压气机非常敏感的特性，初步判断在76%高压转速附近中测点振动增大是由于高压压气机不平衡引起。

为了证实该判断的正确性，对11364 r/min高压转速(90%NH)下中、后测点的信号进行分析，如图(3)和图(4)所示。

分析图3和图4可得，在90%高压转速下中、后测点的信号被分解为4阶IMF和一个剩余分量。分析图3(a)可知，中测点的原始信号存在削波现象，表明高压压气机转子和静子机匣发生了碰摩。第三阶IMF很好地展示了发生碰摩的采样时刻，即在开始阶段、200采样时刻左右、600采样时刻左右、800采样时刻左右和1200采样时刻左右系统发生了碰摩。图3(b)第一阶和第二阶IMF分量的瞬时频率在200采样时刻左右和1200采样时刻左右频率存在突变，也表明在这两个时刻附近系统发生了碰摩。另外第三阶IMF的幅值和瞬时频率从1400采样时刻开始明显变小，进一步表明系统在1400采样时刻左右开始脱离碰摩状态。

图3(a)第三阶IMF的幅值相对于其他阶IMF的幅值明显增大，意味着发生碰摩时系统能量主要集中于第三阶IMF。图3(c)的边际谱也证实了低倍频分量非常大以致工频都被淹没。这表明发生碰摩时转、静系统并非整周期接触，而是遵循“碰摩—弹开—碰摩—弹开…”的过程。

图4(a)后测点的各阶IMF虽然没有直接反映高压压气机的碰摩故障，但图4(c)的边际谱中与碰摩周期相对应的低倍频分量与系统工频相当，反映出了高压压气机的碰摩故障。傅里叶谱虽然也表明系统低倍频分量较大，但对于系统是否发生碰摩，以及碰摩的演变过程等无法作出判断。

因此，可得系统在12134 r/min(96%NH)高压转速附近，中测点振动超限报警是由于高压压气机转静子发生碰摩导致振动过大所引起。

对于减速过程中，高压转速8216 r/min(65%NH)左右中、后测点的信号分析结果与图1和图2类似，也表明高压压气机不平衡导致中、后测点振动增大。

综合图1～图4可得该台发动机在加速过程中当高压转速上升至9606 r/min(76%NH)左右时，由于高压压气机不平衡导致中测点振动增大，随着转速的增加振动值有所减少。当转速增至12134 r/min(96%NH)左右时，高压压气机转静系统发生碰摩，从而引起中测点振动超限报警。在减速过程中虽然系统退出了碰摩状态，但不平衡量依然存在，因此在8216 r/min(65%NH)高压转速附近，中、后测点的振动值增大。

发动机分解检查发现，高压压气机转子存在较大的不平衡量，且静子机匣内壁存在摩擦的痕迹，证实了EMD和HHT用于航空发动机转子—机匣振动信号分析的有效性。

3 结论

将EMD和HHT方法引入到航空发动机的转子—机匣振动信号分析中，并对某台发动机的台架实测信号进行了分析。所得主要结论:

(1)EMD方法根据信号的局部时间特征尺度，能够把复杂的机匣振动信号分解为有限个IMF和一个剩余分量。各阶IMF的希尔伯特谱清楚地表明了频率随采样周期的动态变化特性;

(2)边际谱与傅里叶谱相比较能够更真实客观地反映系统的频率和幅值分布;

(3)通过EMD和HHT能够较为清楚地再现转静系统碰摩故障随转速和采样周期的演变过程，克服了傅里叶谱无法同时获得时域和频域信息的缺陷。

［1］徐可君，江龙平.基于Lyapunov指数能谱熵的转子－机匣系统故障诊断研究［J］.机械强度，2007，29(4):557 －561.

［2］江龙平，徐可君，秦海勤.基于Lyapunov指数谱的转子－机匣系统故障诊断研究［J］.振动与冲击，2007，26(5):49－51.

［3］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London，Series A，1998，454:903 －995.

［4］Cheng J S，Yu D J，Yang Y.A method for gear fault diagnosis based on the empirical mode decomposition［J］.Internationl Journal of Plant Engineering and Management，2004，4(9):230－235.

［5］Loh C H，W u T C，Huang N E.Application of the empirical mode decomposition-Hilbert spectrum method to identify nearfault ground-motion characteristics and structural responses［J］.Bullet in of the Seismological Society of America，2001，(91):1339－1357.

［6］樊长博，张来斌，王朝晖，等.基于EMD与功率谱分析的滚动轴承故障诊断方法研究［J］.机械强度，2006，28(4):628－631.

［7］高 墙，杜小山，范 虹，等.滚动轴承故障的EMD诊断方法研究［J］.振动工程学报，2007，20(1):15－18.

［8］钟佑明.希尔伯特－黄变换局瞬信号分析理论的研究［D］.重庆:重庆大学，2002.

［9］秦海勤，徐可君，江龙平.某型发动机机载振动监测测振点选择研究［J］.推进技术，2007，28(6):697 －700.