高频雷达海杂波的多重分形建模方法研究

盛 文 任 吉

（空军雷达学院，湖北 武汉 430019）

1.引 言

建立在高频雷达海杂波特性分析基础上的目标检测问题，是目前国内外研究中有待突破的一个难点。目前，针对海杂波特性分析研究还主要集中在微波波段［1］，尽管高频段海杂波特性与微波波段呈现出大体相似的特性，但是由于缺乏必要的实验手段和具体数据，国内外针对高频雷达海杂波特性分析的研究非常少。更重要的是，如果通过建立专门的试验设备开展研究工作花费巨大，而且利用实装获得实测数据的途径十分有限，因此，建立高频雷达海杂波的模型就显得尤为必要。传统的杂波机理建模需要定量地描述散射单元的特征，这导致了杂波机理模型往往是极其复杂的且计算量巨大［2］。统计建模将杂波描述为无显著特点的、普适的平稳随机过程，而近年来的研究证明统计模型显然忽视了某种非线性和非平稳的特征。由于人们缺乏对海杂波本质的足够认识，至今都没有任何数学或者物理的解释来支持统计建模，同时也没有看到海杂波其实只是“貌似”随机的过程［3］。

随着Benoit Mandelbrot提出分形理论，为研究海杂波特性提供了崭新的思路和理论工具。近年来，研究海杂波领域的学者们也注意到，基于刻划分形特性的不变量的目标检测在海杂波研究中具有重要的意义，并取得了令人满意的效果［4－9］。另一方面，基于分形理论对海面的描述［10］和对海杂波建模也受到了相当程度的重视。我国学者王红光等［11］利用分型布朗运动（Fractional Brownian Motion，FBM）模型为海杂波建模，并基于分形模型对目标检测进行了研究。随着多重分形（Multifractal）理论被引入时间序列分析，许多学者发现海杂波数据往往并不能用简单的分形模型来刻画，而多重分形可能会取得更好的效果，并利用多重分形方法对海杂波特性进行了分析，得到较好的结果。本文重点讨论多重分形在海杂波时域分形建模中的应用，利用高频雷达海杂波具有的多重分形特性建立高频雷达海杂波的时域分形模型，并通过与实测数据的多重分形性的对比和统计特性验证分析，得出了仿真的高频雷达海杂波具有先验的统计特性的结论，同时也证明了海杂波时域多重分形模型的合理性和有效性。

2.分形理论与海杂波建模

2.1 分形理论

分形是非线性科学研究的主要对象之一，利用分形的方法人们就可以利用分形参数来刻画自然界中的某些复杂现象。分维数是刻画分形的一种重要参数，基本的理论介绍如下。

2.1.1 时间序列分维数的估计

分维数是最重要的分形参数之一，也是分形特性的度量。人们提出了许多分维的估计方法。本文采用相关分形维数来刻画海杂波序列的分形特征。其估算方法可以归纳如下：首先对时间序列｛x1，x2，...，xN｝ 进行相空间重构，对于任意给 定的正数r＞0得到m维相空间 ｛Y1，Y2，..，Ym｝ ，计算所有的距离‖Yi－Yj‖∞＜r对应的点对在所有的点对中所占的比例Cn（r），即

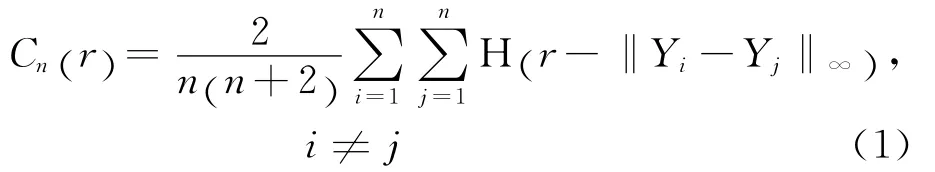
式中：H（）·为Heaviside单位函数，即

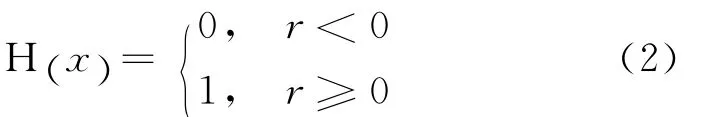
则相关分形维数D可以表示为

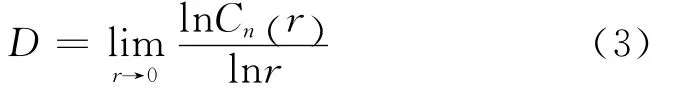
长程相关Hurst指数与分维数的关系为

2.1.2 多重分形理论

多重分形分析的方法有很多，主要有q阶矩结构分割函数法、消除趋势波动分析法（MF－DFA）和基于标准配分函数（统计矩）法、计盒方法，采用q阶矩结构分割函数法进行分析。对于给定的时间序列x（n），使用q阶矩结构分割函数法进行多重分形分析的步骤如下：

1）构造归一化序列｛xi｝，且有xk≥0，

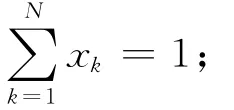
2）将序列｛xi｝分为v个长度为s的子区间，这样可以得到每个区间上的盒概率为

式中Ns＝［N／S］；

3）由此可以得到q阶分割函数

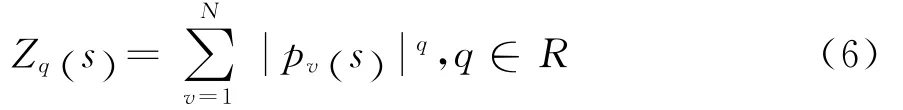
对变量s，在数学意义上，如果某一序列为多重分形序列，那么就满足幂律关系

式中：τ（q）为质量指数，与q呈非线性关系，且非线性程度为多重分形性的度量。奇异吸收子作为几何学对象通常是多重分形的。从这个意义上讲，一个完整的奇异吸收子可能是被分割成了许多或者可能是无限多子集，每一个子集有自己的分维数，并且在原始吸收子中它们的权重是适当地定义的［12］。

刻画多重分形的另外一个重要指数是奇异指数α（q），也是质量指数τ（q）与q呈非线性程度的度量，即多重分形性强弱的度量。α（q）可以由质量指数τ（q）的微分得到，即

定义

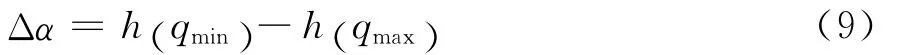
为多重分形性程度，显然Δα越大，质量指数τ（q）与q呈现非线性程度越明显，多重分形就越强。

2.2 分形理论与海杂波建模

基于分形理论的海杂波建模主要分为基于分形海面的散射机理模型和简单的时域模型。文献［13］根据海面的分形特性将被保留在雷达回波中，给出了海杂波散射机理模型。但是，经过分析可以发现：该模型的计算相对复杂且计算量巨大。下面介绍另一种便于计算的方法——时间序列的分形模型。

直接对回波建立时域建模是分形理论在海杂波建模中的另一应用，其优点在于可以用一个简单的迭代函数系统（IFS）和较少的参数产生复杂的信号。如果已经知道海杂波具有分形特性且已知海杂波的分形参数就可以反演出海杂波的时间序列，或者再加入目标信息即可得到一般目标的回波。最常见的由Weiestrass函数法、FBM增量法和小波三种方法产生。

以上三种FBM信号产生方法均满足或近似满足FBM的定义，产生的FBM信号也比较理想，但也存在一些问题。FBM增量法中，增量满足相关性，但还存在一定的差距；小波方法则要求所选用的小波应具有高阶原点矩为零的特点，而且阶次愈高愈好；Weiestrass函数法产生的FBM信号的模型相对比较理想。

但是，文献［14］研究表明高频雷达海杂波可能为具有多个单一分形的组合并且海杂波具有多重分形特性。由此可见，假设海杂波是单分形的时间序列会得到错误的结论。所以，从概率的意义上讲，作为一个“完整的”具有多重分形特性的奇异吸收子的海杂波来说，它的精确的分维数值是无法确定地得到，而可能出现的分维数值只是以一定的机率呈现出来，当测量的次数无限大的时候，就可以近似地得到其分维数的概率密度函数。

3.高频雷达海杂波的时域分形模型及其仿真计算

3.1 高频雷达海杂波的时域分形模型

基于以上分析，高频雷达海杂波可以看作是大量单一分形在概率意义上的线性组合，不同分形具有特定的权系数，这些权系数可假定满足如下条件

1）权系数之和为1，即

式中：n反映模型的复杂度，显然其值越大仿真的模型越精确。由此，每个分量对应的权值可以看作某一随机事件的概率，而所有的概率之和为1。显然，就可以假设所求的权系数为某一随机事件的概率分布，本文主要针对均匀分布、正态分布和χ2分布等几种常见的分布形式进行分析。

2）每个单一分形序列的分维数Di为均匀分布，且已知模型整体上表现出来的分维数D0应位于所有可能的分维数Di的几何中心，即

由此，如果权系数为一正态分布的概率密度函数的形式分布，就可以看作是中心分维数在构造的多重分形的时间序列中贡献最大。

3）最优权遵循误差最小原则，即

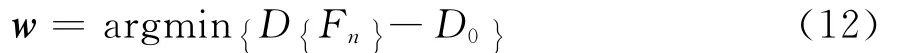
根据以上假设，得到的海杂波时域分形模型为

式中：wi为单一分形的权系数；fi为单一分形，对应的分维数为Di，即D｛fi｝＝Di，D｛·｝表示求分维数，单一分形fi为简单的分数布朗运动。

本文采用的海杂波数据是在HF波段雷达上采集到的海面后向散射回波信号。根据2.1.1节估算相关分维数的方法，计算了本文所有256批实测的高频海杂波周期积累信号的分维数，得到分维数的均值为1.732。这就是多重分形的分维数的几何中心，即所有的实测数据整体上表现出来的分维数。

3.2 高频雷达海杂波模型的仿真计算

在简单地分析了均匀分布、正态分布和χ2分布等几种常见的分布形式之后，可以发现，在满足3个假设的情况下，正态分布形状N（D0，σ2）的权值能较好地刻画出多重分形的时间序列。基于此，将在满足3个假设的前提下，采用具有正态分布的概率密度函数形状的权值对单一分形序列加权求和来描述多重分形序列，即杂波数据的时域多重分形建模。当复杂度系数n选定以后，分布的中心为实测的高频海杂波分维数的均值1.732，此时只需要对分布的形状——“胖瘦”进行一维搜索即可。具体仿真流程如图1所示。

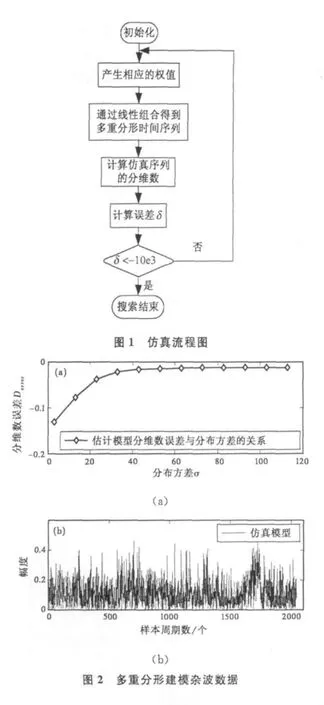
为了保证新建立的模型精度和仿真速度，选取复杂度系数n＝50进行仿真计算。权值的搜索过程为：将分布方差σ2＝［0，100］平均地分成10份，在每一份进行100次搜索（即最小的搜索步进为0.1），观测每一次的分维数的误差。可以看出：将10次搜索中每一次的最小值显示在图2中，由图2（a）可以看出：当仿真多重分形权值分布的方差达到62.9时，模型就具有稳定收敛的误差，此时得到的时域模型显示在图2（b）中。

4.高频雷达海杂波模型的验证分析

模型的验证分析主要是考察时域多重分形模型、FBM模型和实测数据的多重分形性的相似性。利用质量指数函数和奇异指数来度量多重分形性的强弱，从而验证多重分形模型比FBM模型更加能够匹配实测数据的多重分形性。除此以外，为了更加严谨，验证仿真杂波数据与高频雷达海杂波的统计特性，将比较仿真数据与最可能模型幅度分布的概率密度函数（Probability Density Function，PDF）。为进一步考察两个分布的拟合优度，对仿真数据的“拖尾”与由参数估计得到的理论分布模型做了修正的K－S检验。

4.1 分形模型的多重分形性验证

首先对海杂波时域模型进行多重分形特性验证。利用q阶矩结构函数分割法［15］对海杂波时域模型做多重分形分析。图3是q为－20～20，步长为4共11组值时的双对数关系图。可以看出整体上呈现了很好的线性关系，因此，满足式（7）中的幂律关系，即说明在规定的尺度变化范围内海杂波模型具有无标度性，也就是说海杂波模型具有分形的特性。

为了比较仿真模型与实测数据的多重分形性的相似性，同时为了说明仿真模型比文献［11］的FBM模型具有更强的多重分形性。首先产生256批符合最优权值的多重分形模型，再利用文献［11］中的FBM模型产生256批分形数据。然后分别计算实测数据、FBM模型和多重分形模型数据的质量指数函数τ（q）和奇异指数α（q）的误差图，分别显示在图4、图5和图6中。

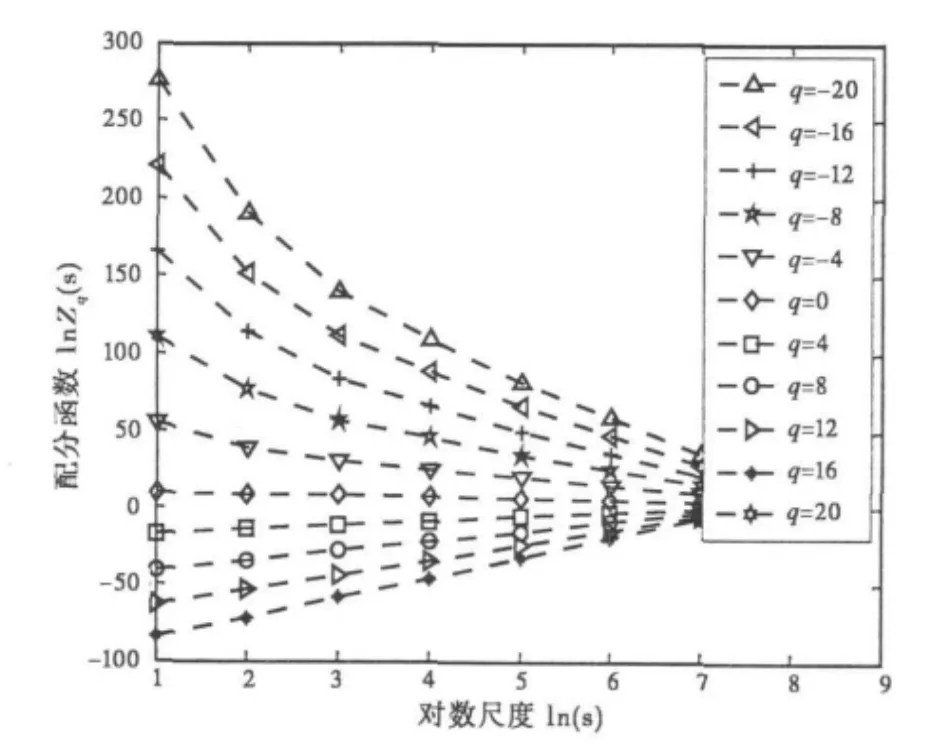
图3 配分函数lnZq（s）与对数尺度ln（s）的关系

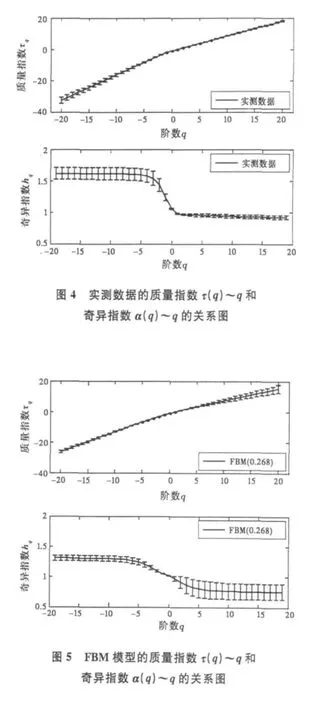
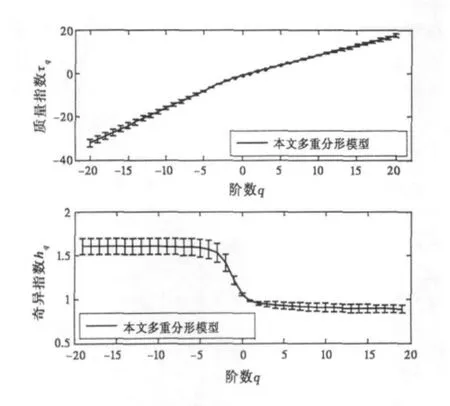
图6 多重分形模型的质量指数τ（q）～q和奇异指数α（q）～q的关系图

从图4～6可以看出，三种数据的质量指数函数τ（q）都是q的一个上凸的函数，即τ（q）与q之间都存在着较强的非线性关系，这表明了三种数据都具有一定的多重分形的特性。同时可以注意到，实测数据和多重分形模型比FBM模型具有更为明显的弯曲，即实测数据和多重分形比FBM模型具有更强的多重分形性。同时多重分形模型和实测数据的Δα都比FBM模型的Δα要大，也能反映实测数据和多重分形比FBM模型具有更强的多重分形性。除此以外，可以很清楚地看出：多重分形模型比FBM模型更加能匹配实测海杂波数据的多重分形性。这就证明了多重分形模型的合理性。

4.2 多重分形模型数据与经验统计估计模型的PDF比较分析

首先对仿真数据分别估计瑞利分布（Rayleigh）、韦布尔分布（Weibull）和对数正态分布（Log－Normal）模型的相关特征参数，由表1给出。然后与理论模型比较由仿真数据估计的经验分布（柱状图），同时为了观察我们感兴趣的数值较小的尾部数据的特性，将结果在对数坐标下显示出来，如图7所示。同时将实测数据的估计经验分布也附在图7中，由仿真结果可以清楚地看出：多重分形模型不存在长的拖尾现象，数据幅度接近瑞利分布。这与文献［16］认为低分辨率雷达海杂波的幅度统计特征接近瑞利分布的研究结论是一致的，而且分形模型的分布与实测数据的分布具有相似性，从而进一步说明了海杂波时域多重分形模型的合理性。

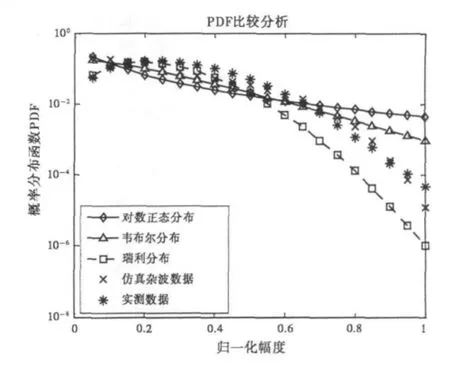
图7 仿真数据与估计模型的概率密度函数比较分析

表1 仿真杂波数据的模型参数估计

4.3 多重分形模型数据的K－S统计检验

为了进一步检验拟合优度，我们使用一种修正的两点K－S统计检验。标准的两点检验验证两个随机序列是否具有相同的分布。在标准的检验中使用了分布的整个定义范围内的数据，而在修正版中，只用一部分数据［17］。因为拖尾的数据直接影响对目标的检测，所以我们对拖尾的数据特别感兴趣。固定不同的门限值并且只考虑比门限值更大的采样值。对于不同的门限值，在原假设为真的前提下，将由参数估计得到的理论积累分布函数（Cumulative Distribution Function，CDF）与仿真数据构造的经验CDF相比较，若它们的最大差别大于临界值，则拒绝原假设，反之亦然。

利用K－S检验方法分别对两个不同的门限值，即门限1和门限2，分别表示标准两点检验和其幅度值大于0.667（它可以将拖尾数据隔离开来）的数据进行了检验，结果如表2所示。其中α表示显著性水平，H的值为1就表示最大偏差量De大于临界值Dcri，同时拒绝原假设，反之亦然。可以清楚地看出，对全部数据（门限1）的检验结果可以发现，这3种典型的分布都拒绝了原假设，即仿真数据不服从这3种假设分布中的任何一种。但是也可以看到，瑞利分布的最大偏差值最小，几乎达到了临界值，这也验证了前面由仿真数据估计的PDF比较分析结果——仿真数据幅度近似服从瑞利分布，这与先验的海杂波的统计特性是一致的。更进一步，对于我们感兴趣的尾部数据（门限2）进行检验发现，当显著水平为0.05和0.1的时候，对数正态分布和瑞利分布都可以接受原假设。但是，当进一步提高显著性水平到0.2的时候，只有瑞利分布可以接受原假设，进一步地说明高频雷达海杂波时域多重分形模型幅度具有瑞利分布的统计特征。

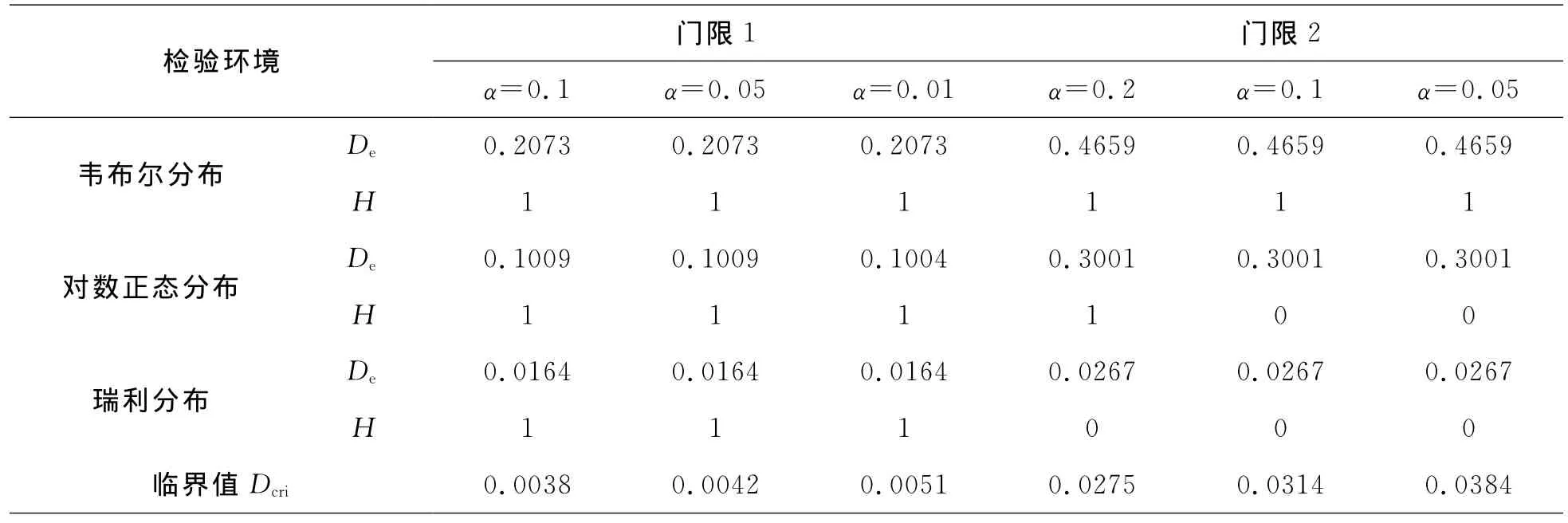
表2 柯尔莫哥洛夫－斯米尔洛夫检验

5.结 论

本文重点讨论分形理论在海杂波建模，特别是在高频雷达海杂波的时域分形建模中的应用。在高频雷达海杂波多重分形特性的基础上建立高频雷达海杂波的时域分形模型，通过对韦布尔分布、对数正态分布和瑞利分布3种最常用的海杂波幅度的概率密度函数的比较分析并且利用修正的K－S统计检验，得出了高频雷达海杂波的多重分形模型具有瑞利分布的统计特性的结论，证明了海杂波时域多重分形模型的合理性，这对于高频雷达海杂波建模与仿真及其背景下目标检测研究具有现实意义。

本文的一个最基本的限制就是：由于实测数据有限且对海杂波的入射角、极化方式、风速、风向以及海情等先验信息缺乏，所以得到的数据模型可能只匹配与原始观测数据相同或者相似的观测环境的测量数据。在以后的研究中需要在大量实测数据的基础上进行更加全面深入的研究。但是同时也注意到，本文的意义在于从一个新的视角来建立海杂波模型，并且基于非线性理论的高频海杂波模型对于研究海杂波的特性以及目标检测都有现实意义。

［1］扈罗全，林乐科，朱洪波.三种重拖尾分布海杂波的比较与分析［J］.电波科学学报，2007，22（6）：1061－1067.

HU Luoquan，LIN Leke，ZHU Hongbo.Comparison and analysis of three kinds of distribution of sea clutter with heavy tails［J］.Chinese Journal of Radio Science，2007，22（6）：1061－1067.（in Chinese）

［2］BERIZZI F，GRECO M.Fractal approach for sea clutter generation［J］.IEE Proceedings：Generation，Transmission and Distribution，2000，147（4）：189－198.

［3］HAYKIN S.Chaotic characterization of sea clutter：new experimental results and novel applications［J］.Signals，Systems and Computers，Conference Record of the Twenty－Ninth Asilomar Conference on.Pacific Grove，CA，1995，2：1076－1080.

［4］LO T，LEUNG H，LITVA J，et al.Fractal characterisation of sea－scattered signals and detection of seasurface targets［J］.IEE Proceedings－F，1993，140（4）：243－250.

［5］杜 干，张守宏.分形模型在海上雷达目标检测中的应用［J］.电波科学学报，1998，13（4）：377－381.

DU Gan，ZHANG Shouhong.Radar ship targets detection based on fractal model［J］.Chinese Journal of Radio Science，1998，13（4）：377－381.（in Chinese）

［6］GUAN J，LIU N，ZHANG J，et al.Multifractal correlation characteristic for radar detecting low－observable target in sea clutter［J］.Signal Processing，2010，90（2）：523－535.

［7］XU X.Low observable targets detection by joint fractal properties of sea clutter：an experimental study of IPIX OHGR datasets［J］.IEEE Transactions on Antennas and Propagation，2010，58（4）：1425－1429.

［8］LIU N，CHE Z，GUAN J，et al.Fractal－based variable step－size least mean square algorithm for radar target detection in sea［C］／／2009International Radar Conference Radar"Surveillance for a Safer World"（RADAR 2009）.California，USA，2009：1－5.

［9］LIU N B，GUAN J，ZHANG J.Fuzzy fractal algorithm for low－observable target detection within sea clutter［C］／／IET International Radar Conference.Guilin，China，2009：1－4.

［10］郭立新，徐 燕，吴振森.分形粗糙海面电磁散射的波束模拟法［J］.电波科学学报，2004，19（z1）：50－55.

GUO Lixin，XU Yan，WU Zhensen.Beam Simulation method of scattering for fractal rough sea surface［J］.Chinese Journal of Radio Science，2004，19（z1）：50－55.（in Chinese）

［11］王红光，康士峰，张忠治.海杂波的分数布朗运动模型及其应用［J］.现代雷达，2005，27（11）：58－62.

WANG Hongguang， KANG Shifeng， ZHANG Zhongzhi.Fractional brownian motion model of sea clutter and its application［J］.Modern Radar，2005，27（11）：58－62.（in Chinese）

［12］HU J，TUNG W，GAO J.Detection of low observable targets within sea clutter by structure function based multifractal analysis［J］.IEEE Transactions on Antennas and Propagation，2006，54（1）：136－143.

［13］LIN N，LEE H P，LIM S P.Wave scattering from fractal surfaces［J］.Journal of Modern Optics，1995，42（1）：225－241.

［14］GAO J，YAO K.Multifractal features of sea clutter［C］／／Radar Conference，2002Proceedings of the IEEE.LOS ANGELES，USA，2002：500－505.

［15］HO D S，LEE C K，WANG C C，et al.Scaling characteristics in the taiwan stock market［J］.Physica A，2004，332：448－460.

［16］焦培南，张忠治.雷达环境与电波传播特性［M］.北京：电子工业出版社，2007.

［17］FARINA A，GINI F，GRECO M V，et al.High resolution sea clutter data statistical analysis of recorded live data［J］.IEE Proceedings：Radar，Sonar and Navigation，1997，144（3）：121－130.