大型水轮发电机定子绕组谐波及其力波分析

2011-06-03唐博进杜建国张成平

大电机技术 2011年5期

唐博进，吴穹，杜建国，张成平

（中国长江三峡工程开发总公司机电工程部，湖北宜昌 443002）

引言

三峡右岸电站某型号机组发电机定子槽数为 510槽，采用分数槽双层波绕组设计，每相5分支并联，转子磁极为40对极。

此型号首台机组于2007年10月投产，机组运行后直观感觉振动噪音较大，站在上盖板上有麻脚感，且能听到“嗡嗡”的振动噪音。经测量发现机组定子铁心振动较大，频谱分析表明其中100Hz分量偏大。在650MW 负荷下，定子铁心 100Hz振动幅值达到了73.5μm。

1 振动原因分析

引起该机组铁心100Hz振动的可能原因有两个：一个是定子绕组并联支路间的环流引起的分数次谐波磁场；另一个是定子绕组大小相带布置方式引起的分数次谐波磁场。

该型机组的定子绕组设计满足分数槽双层波绕组支路对称条件[1]，绕组支路对称设计，各支路的电动势完全相等，理论上并联支路间环流为零。为此，测试了定子绕组在断开各并联支路前后、空载工况下定子铁心的振动幅值。结果表明，定子铁心100Hz振动均在5μm以内，这从实践上证明支路间环流对定子铁心100Hz振动影响不大。环流不是引起铁心振动的原因。

大型水轮发电机组定子绕组常采用分数槽设计，绕组电流在定转子间气隙中可能产生分数次谐波磁势，且各次谐波的分布系数不相同[2]。分数次谐波与基波磁场相互作用，在铁心中产生力波节点，可能会引起铁心振动。尤其是这类谐波中极对数接近基波极对数的反转谐波，其在铁心中产生的力波节点数较小，因而可能引起较大的振动。

2 分数槽绕组磁动势谐波分析

分数槽绕组在各相带内的极相组有大有小，第二对极下的各相导体，不一定是第一对极的重复，一个单元电机[3]才形成一个完整的周期。如果设此周期为T，对应的角频率ω= 2 π /T，从傅里叶分析可知，此周期内的波形可分解为一系列谐波：

其中1,2,k=∞…，ka是各阶谐波的幅值系数，kθ是于各阶谐波初始相位角。

为了避开实际定子绕组中每相有多个并联支路的干扰，假定单元电机中每相均只有一个支路。从单元电机的角度分析各次谐波产生的原因及大小。

设每相槽数为N，其大小相带槽数分别为1N、2N则大小相带槽数之和等于每相槽数，即将单元电机中各槽按照其对应的电角度映射在 0～2π 的相位圆周上，并按顺序对各槽重新编号，可以画出极相带布置表格，见表1。

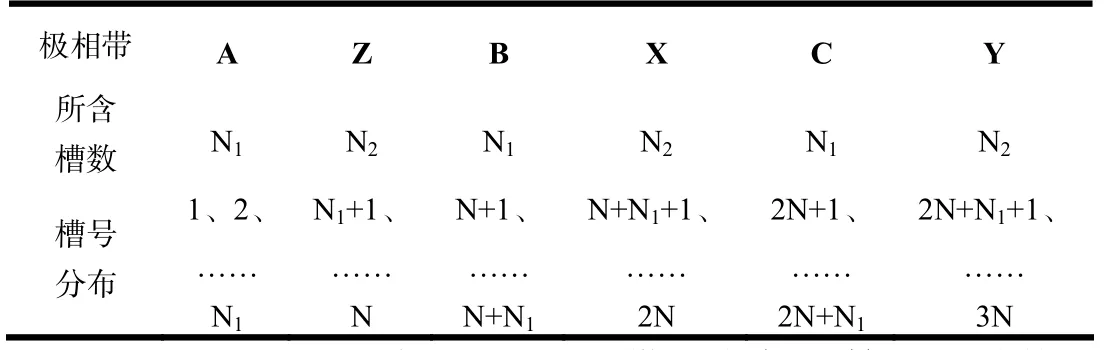
表1 单元电机极相带布置表格

至此，可以根据A-X极相带，方便的算出磁动势分布系数，以基波为例：

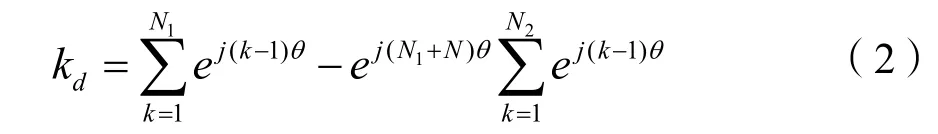
其中θ是同一相带中相邻槽之间的空间电角度，它满足：

其中Y为整数，是定子绕组的跨距[3]；α是定子相邻槽之间的电角度；Q是定子总槽数；P是电机的磁极对数。如果是谐波，设谐波次数为ν，则ν次谐波的磁动势分布系数为：

从（1）式中知道若以单元电机为一个周期，设对应的角频率为ω0，则第k次谐波的频率为kω0；单元电机中含p对磁极，因此实际谐波的次数为ν=k p，于是出现了分数次谐波。当k＜p时就是低次谐波，k=p时就是基波，k＞p时就是高次谐波。需要注意的是，由于单元电机中含有3相且每相绕组的空间分布相差 120°，因此对单元电机而言不存在k= 3n(n= 1 ,2,…) 次谐波。

该大型水轮发电机定子总槽数Q= 5 10，极对数P= 4 0，则每极每相槽数：

其中m是相数，此处为3；b、c、d为整数，且c、d互质。

根据定子绕组的基本参数可知，机组的单元电机数为[2]：

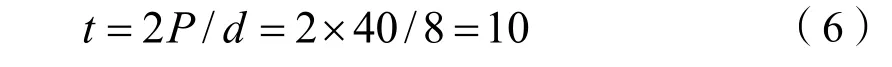
其中每个单元电机的磁极数：

每个单元电机槽数：

单元电机每相槽数为：

该大型水轮发电机的定子绕组跨距 13Y= 。将其与 510Q=、40P= 一并代入（3）与（4）式，可以得到单元电机各种大小相带布置方式下各次谐波的绕组分布系数，见表2。

表2 某机组单元电机大小相带布置谐波分布系数

虽然表2计算的是单元电机中各次谐波的分布系数，但实际上也是整个发电机的各次谐波分布系数。不同之处在于整个发电机含有10个单元电机，因此谐波极对数相应要乘以10。

3 磁动势谐波的力波分析

该机组气隙磁场中存在10对极、20对极、50对极、70对极、80对极等谐波。这些谐波与定转子间气隙中的基波磁动势互相作用，对定子铁心形成了力波。力波的节点数越少，对定子铁心振动的影响就越大。

以 20对极的磁动势谐波为例，将其与基波（40对极）磁动势沿定转子气隙展开画在同一张图中，如图1所示，横坐标上每一格对应于实际的一个磁极宽度。其中，基波磁动势向正（右）方向运动，20对极的谐波磁动势向反（左）方向运动。

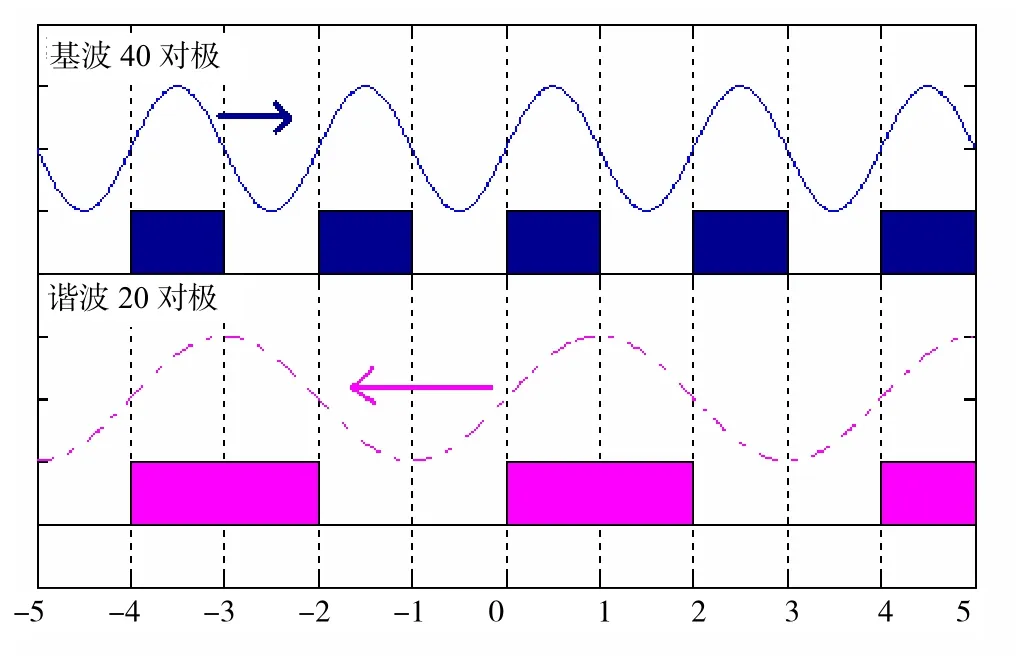
图1 基波与20对极谐波相互作用图

从图1中可以看出，每4个磁极的宽度中，基波与20对极谐波形成一个共同周期，那么二者间的相互作用力也在4个磁极的宽度内形成一个周期，即力波的波长为4个磁极宽度（即2对磁极的距离）。整个发电机转子有80个磁极，因此共有80/4=20个力波周期，也就是说20对磁极与基波形成的力波在定子铁心中有20个力波节点。

力波随着基波与20对极谐波的运动而运动，将基波与20对极谐波的正半波化为一个方波，负半波化为0，如图所示。如此形成了两个类似梳子齿部的图形，下面通过此“梳齿模型”来分析力波的传播速度。

假设有两把梳子A、B齿距不同，分别为SA、SB，且SA＞SB。如果把这两把梳子互相叠在一起，透过二者的齿部看亮光则可以看到亮段和暗段相互交替出现，形成周期性变化。这类似于磁动势相互作用形成的力波。使两把梳子之间有相对运动，可以看到亮带和暗带也以一定规律运动。若推导出此时亮带和暗带的运动规律，则实质上等效于求出了力波的传播速度。

将两把梳子的某个齿重叠在一起，则下一对齿错开的距离为S=SA-SB（SA＞SB）。保持梳子A不动，移动梳子B一个S的距离，则亮带和暗带的图像将移动一个梳子A的齿距SA。那么亮带和暗带的移动速度为：

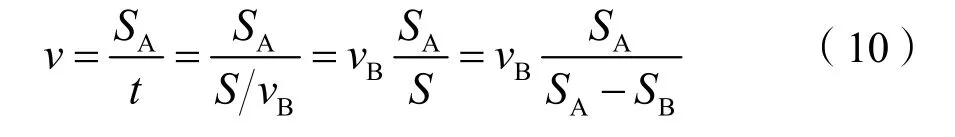
其中，Bv是梳子B的速度，由于梳子A不动，Bv其实就是二者的相对速度。于是（10）式化为：

此时，亮带和暗带相对梳子A的移动速度为v。

应用上述模型，将基波与20对极谐波看作“梳子”，则可以通过式（11）算出力波的传播速度。基波速度设定为v′，则根据谐波理论，20对极谐波的速度为-2v′，负号表示方向相反。基波相对20对极谐波的速度为v′相对=3v，根据式（11），可以算出力波相对 20对极谐波的速度为由于20对极谐波实际速度为 2v′- ，则力波在定子铁心中的传播速度为这意味着在一个工频周波的时间内基波旋转经过1对磁极的空间距离，而力波已经传播了4对磁极的空间距离。前文已经推导出此力波的波长是2对磁极宽度，那么由20对极谐波引起的力波的频率：

其中0f是工频。应用上述方法，本文推导出10对极、50对极、70对极、80对极谐波形成的力波的波长（以磁极对数表示）、节点数、速度与频率，见表3所列。

表3 各次磁动势谐波所产生的力波的特性

表3所示，10对极和70对极这两个谐波，它们与基波相互作用产生的力波是静止的。这表明在此种力波作用下，虽然定子铁心沿气隙展开在不同的空间角度位置受力大小不一样，但同一位置上随时间变化受力大小保持不变，因此铁心在此种力波下只发生形变而没有振动。

而20对极、50对极和80对极这三个谐波，它们与基波相互作用产生的力波频率均是 100Hz。因此定子铁心在这些100Hz的力波下，发生强迫受激振动，振动的频率与外力频率吻合，也是 100Hz。这很好的解释了水轮发电机组定子铁心含有100Hz振动分量的现象。

4 改造方案与改造效果

谐波与基波相互作用产生的100Hz力波使铁心发生振动，所以消除铁心100Hz振动的有效方法就是削弱对应的谐波。由于谐波的次数越高能量越小，因此我们只考虑20对极、50对极、80对极这三个谐波，更高次的谐波因能量很小对铁心的振动影响不大。

50对极谐波所产生的力波节点只有10个，它对定子铁心振动的影响是最大的；其次是20对极谐波，其产生的力波节点有20个；影响最小的是80对极的谐波，它的能量比前二者都小，并且产生的力波节点数最多，达到40个。

表 2中列出了定子绕组多种可能的大小相带接线方式下各次谐波的分布系数。该机组原有相带布置是“N1+N2= 1 0 + 7 ”。从中可以看出只有“N1+N2= 1 2 + 5 ”方式满足其20对极和50对极谐波均小于原有的“N1+N2= 1 0 + 7 ”方式，因此改为“N1+N2= 1 2 + 5”方式是最优选择。此改造方案下80对极谐波比原有方案稍有增大，但考虑到80对极谐波较小，力波节点数较多，因此不会造成定子铁心振动的加大。需要指出的是，按照此方案改造后基波系数由0.951下降为0.933，略有减小。

对该机组按上述方案进行了定子绕组大小相带布置改造。改造前后定子铁心振动数据见表4。