基于最大不失磁电流的表贴式永磁电机性能分析*
2011-06-02毕刘新王善铭杨平西
毕刘新, 王善铭, 杨平西
(1.中船重工集团公司第704研究所,上海 200031;2.清华大学电机工程与应用电子技术系,北京 100084)
0 引言
钕铁硼的应用使永磁电机的功率密度和效率都有了很大提高,表贴式永磁电机卓越的控制性能使其在变速驱动系统中得到了广泛应用,但是永磁体的潜在失磁危险一直制约着其在高可靠领域的应用[1-2]。高温、剧烈震动及冲击电流产生的电枢反应均可造成永磁材料的不可逆去磁,使电机性能降低甚至无法使用[1]。本文仅关注于电枢反应产生的去磁效应,通过建立最大不失磁电流与永磁电机结构尺寸之间的关系,推导出电机的运行极限,为永磁电机的设计以及变频器供电情况下的安全运行提供依据。
文献[3]分析了永磁材料在快速交变磁场作用下的磁化和退磁规律,并在此基础上初步探讨了永磁材料的交流失磁机理。文献[1-4]分别用磁路法和有限元法对永磁电机的失磁特性进行了研究,但均不够简单直观。文献[6-9]研究了电枢电流对永磁电机的去磁特性,但没有据此对电机的性能进行更深入的研究,也未推广至多相电机。
本文根据永磁体的退磁特性,推导了表贴式永磁电机的最大不失磁电流解析计算公式,分析了电机的相关性能与提高的措施,且本文公式均可用于多相永磁电机,最后通过有限元仿真,验证了最大不失磁电流解析计算公式的正确性。
1 最大不失磁电流
1.1 永磁电机的结构描述
图1为表贴式永磁电机的结构示意图,齿槽效应通过卡氏系数计入,图中的气隙长度为有效气隙长度。
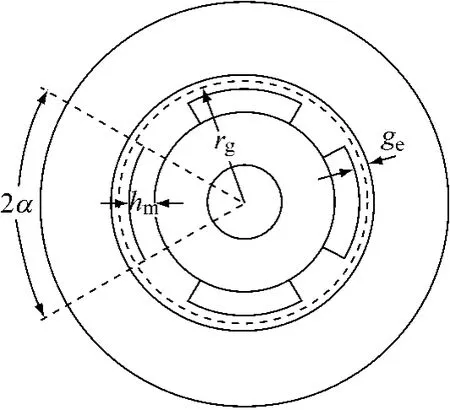
图1 表贴式永磁电机横截面示意图
图中:ge——有效气隙长度;
hm——永磁体厚度;
rg——气隙半径;
2α——每极下永磁体覆盖的电角度。
1.2 钕铁硼永磁材料的退磁曲线
典型的钕铁硼永磁材料的退磁曲线如图2所示,D点称之为拐点,D点以上部分的回复线同退磁曲线重合为一直线,永磁电机的磁性能在该区间保持稳定,一旦退磁磁场强度超过Hd后,退磁曲线急剧下降,此时回复线与退磁曲线不再重合,造成永磁体的不可逆去磁,进而导致电机的性能变差。因此,永磁电机在运行中必须保证永磁体的退磁磁场强度不得超过Hd。
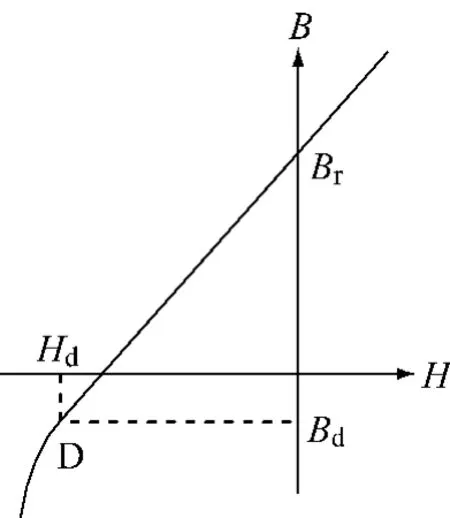
图2 钕铁硼永磁材料的退磁曲线
图中:Br——永磁体的剩磁密度;
Bd——失磁点对应的磁密。
1.3 最大不失磁电流推导
图3所示为永磁磁极和定子电枢电流共同产生气隙磁密的过程,忽略铁心饱和,其中β是定子磁动势轴线超前转子d轴的电角度,称之为内功率因数角。
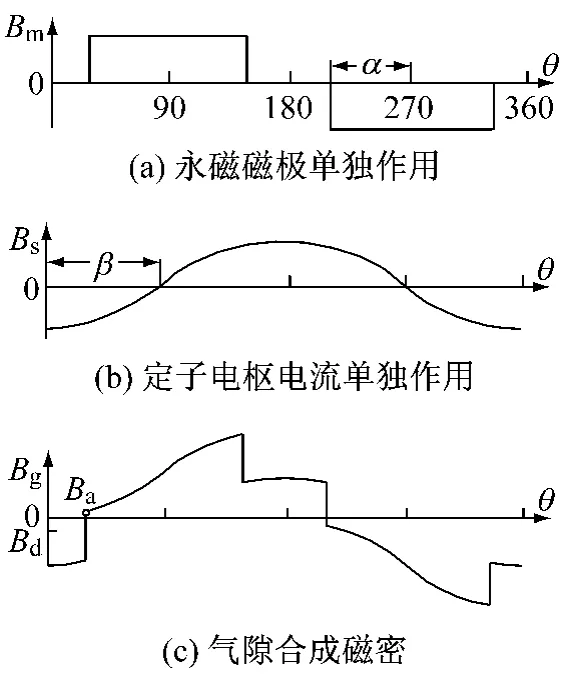
图3 气隙合成磁密示意图
图3(a)为永磁磁极单独作用时产生的磁密分布示意图,其中:
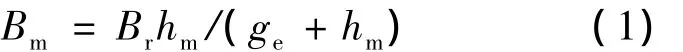
图3(b)为定子电枢电流单独作用时产生的空间基波磁密波形示意图,其磁密幅值为
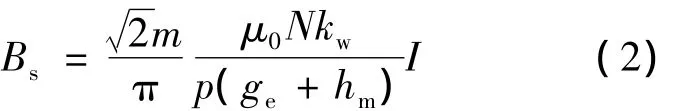
式中:m——电机相数;
N——每相绕组串联匝数;
kw——基波绕组因数;
p——极对数;
I——相电流有效值。
图3(c)为气隙合成磁密示意图,当采用Id=0的控制方法时,β=90°,对应的电枢电流为交轴性质的,此时在图中的黑点标注处永磁体承受最大的退磁磁场强度,为避免不可逆去磁,必须保证Ba>Bd[8],即
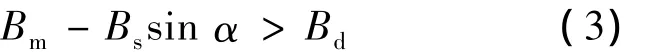
将式(1)、(2)代入式(3)可得到交轴性质的最大相电流有效值:
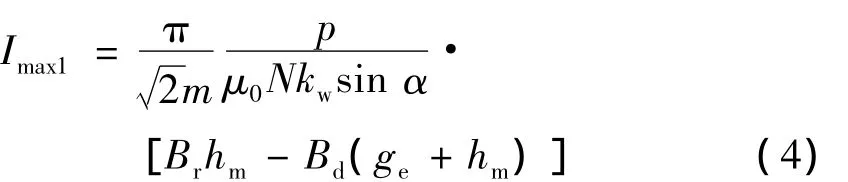
当β=180°时,电枢电流为去磁性质的直轴电流,此时的定子相电流最大值为
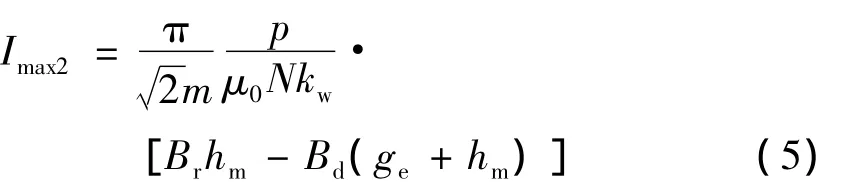
由式(4)、(5)可得出以下结论:
(1)交轴电流对永磁体的退磁效应小于去磁性质的直轴电流;
(2)增加极对数时,每极下的电枢磁动势减小,电枢反应对永磁体的去磁效应减弱;
(3)增大永磁体厚度和采用高剩磁密的永磁体可提高最大不失磁电流。
2 永磁电机性能分析
以最大不失磁电流为基础,可以进行永磁电机的性能分析。
2.1 最大转矩能力
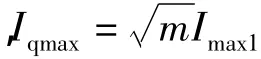
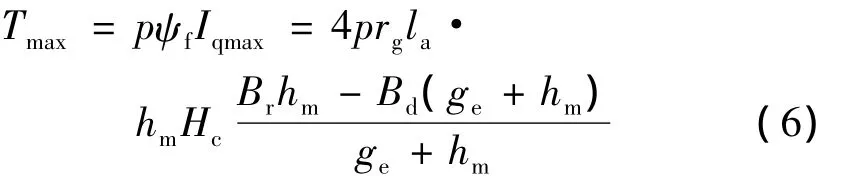
式中:la——电枢铁心长度;
Hc——永磁体矫顽力。
假设Bd=0,则式(6)简化为
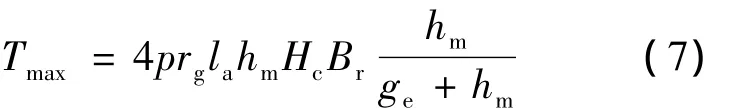
由式(7)可得出如下结论:
(1)最大转矩与电机相数无关;
(2)最大转矩与极对数、气隙半径及电枢长度成正比;
(3)增大永磁体厚度和采用高磁能积HcBr的永磁体可提高最大转矩。
2.2 最大气隙剪切力密度
气隙剪切力为电枢单位表面积的平均电磁切应力,由定义可知:最大转矩对应的气隙剪切力密度为
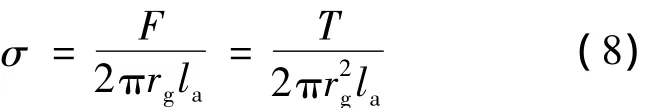
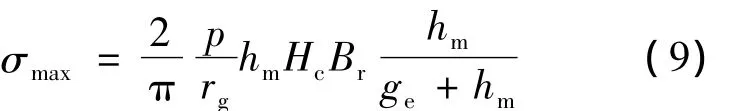
气隙剪切力密度是电机的一个非常重要的指标,表征着单位电机转子体积产生的转矩,反映了电机材料利用率,为提高气隙剪切力密度可采取以下措施:
(1)提高永磁体的最大磁能积;
(2)增加永磁体厚度,尽可能减小气隙长度;
(3)增加极对数,减小转子半径,但是电机设计中,很难兼顾这两点,一般当极对数增加时要相应增加电机的半径。
2.3 最大加速能力
径向电机的转子可以看作一个圆柱体,其转动惯量约为

式中:ρ——转子材料密度。
结合式(7)、(10)可以得到永磁电机的最大加速性能:
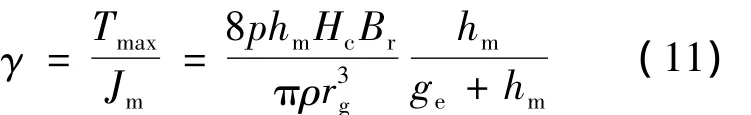
在需要快速响应的场合,往往要求电机具有尽可能大的加速性能,根据式(11)可采取以下措施来提高:
(1)减小转子半径;
(2)增加极对数;
(3)增大永磁体厚度和采用高磁能积的永磁体。
3 有限元验证
由于电机的性能分析是基于最大不失磁电流进行的,因此本文仅对最大不失磁电流进行验证。基本思路是:当电枢绕组通最大不失磁电流时,查看永磁磁极范围内的气隙合成磁密是否等于永磁体失磁点对应的磁密Bd,以此验证最大不失磁电流解析计算公式的正确性。
3.1 仿真用电机数据
本文采用的多相永磁电机的主要参数如表1所示,其中铁心材料采用DW315,具体磁化曲线参见文献[1]后的附录。
根据前文的解析公式计算结果如表2所示。
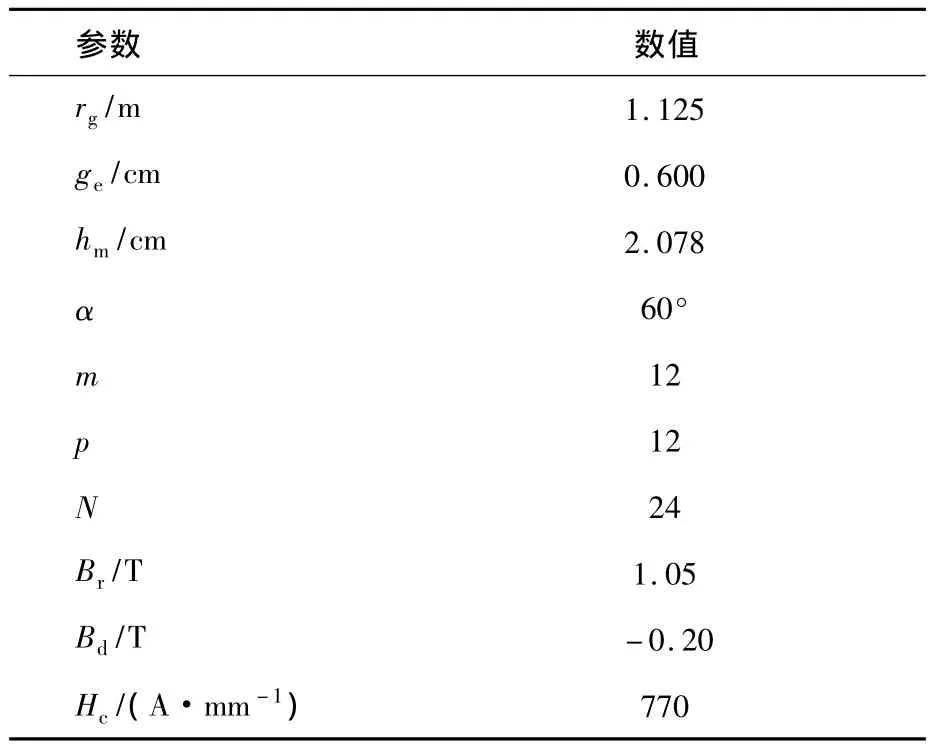
表1 主要尺寸和参数
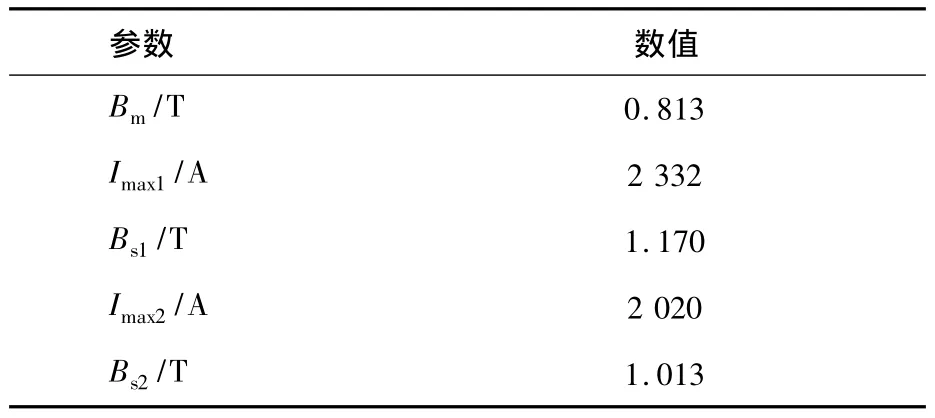
表2 解析计算结果
3.2 有限元仿真结果
本文采用ANSYS仿真软件对电机进行二维的静磁场分析。图4为永磁电机一对极下的有限元模型与网格剖分。其中边界条件设置情况如下:定子外边界和转子内边界磁矢位均设置为0;两侧设置为偶对称周期性边界条件。由于气隙相对很小,可以取气隙中间的径向磁密代替永磁磁极外边缘的磁密。
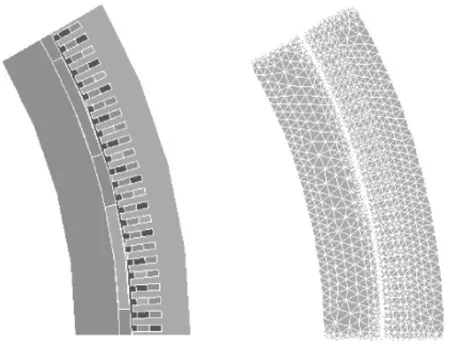
图4 有限元模型与网格剖分
图5(a)为永磁体单独作用时的气隙磁密波形,磁极范围内的磁密平均值与解析解0.813 T非常接近。
图5(b)、(d)分别为 Imax1=2 332 A,β =90°和Imax2=2 020 A,β=180°时,电枢电流单独作用下的径向气隙磁密波形。由于铁心饱和的原因,其基波幅值较解析解稍小。
图5(c)为Imax1=2 332 A,β=90°时的气隙合成磁密波形,其中虚线为(a)、(b)波形直接叠加的结果,实线为实际的合成磁密波形,两者比较可以清晰地看出铁心饱和的影响。实线的加粗部分对应于 60°~120°的磁极范围,其最小值约为0 T,与解析计算结果的-0.2 T有些出入,原因主要在于解析解仅考虑了电枢磁动势的基波效应,且忽略了饱和效应。
图5(e)为 Imax2=2 020 A,β =180°时的气隙合成磁密波形,在直轴去磁性电枢电流的作用下,合成气隙磁密幅值较小,铁心未饱和,因此电枢电流实际的去磁效应比考虑了饱和效应的图5(d)中的要大,更加接近忽略饱和的解析计算结果。但是由于齿槽效应带来的磁导不均匀,在60°~120°磁极范围内,最小磁密值为-0.4T,较理论值-0.2 T稍小,因此在实际应用中,最大不失磁电流的确定需要考虑相应的安全系数。
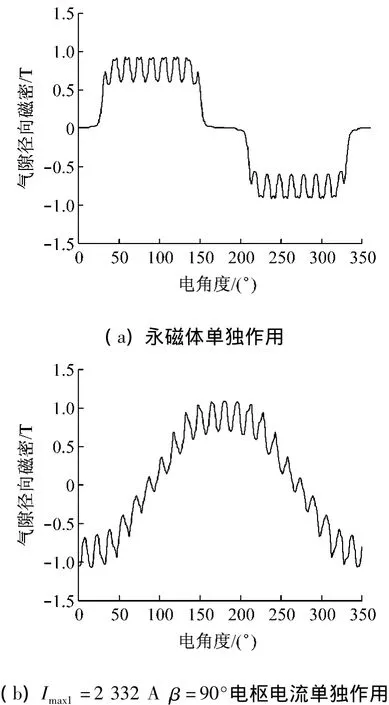

图5 有限元仿真波形
4 结 语
本文在仅考虑电枢电流基波磁动势与忽略铁心饱和的情况下,根据永磁体的退磁特性推导出了永磁电机交轴和直轴性质的最大不失磁电流解析表达式,并以此为依据分析了永磁电机的有关性能,总结了相应的提高措施。这些解析公式将电机的尺寸结构与性能联系起来,为永磁电机的设计和优化,以及变频器供电时运行极限的确定提供了依据。本文中的公式同样适用于多相永磁电机。有限元仿真波形与解析计算结果很好地吻合,证明了本文提出的解析公式的正确性。
[1]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997.
[2]王秀和.永磁电机[M].北京:中国电力出版社,2007.
[3]黄浩,柴建云,姜忠良,等.钕铁硼稀土永磁材料交流失磁[J].清华大学学报,2004,44(6):721-724.
[4]何山,王维庆,吴小艳,等.永磁同步发电机电枢反应去磁效应的分析[J].防爆电机,2005,40(2):8-10.
[5]毕刘新.表贴式多相永磁电机的设计与优化[D].北京:清华大学,2009.
[6]Sebastian T,Slemon G R.Transient modeling and performance of variable-speed permanent-magnet motors[J].IEEE Transactions on Industry Applications,1989,25(1):101-106.
[7]Sebastian T,Slemon G R.Operating limits of inverterdriven permanent magnet motor drives[J].IEEE Transactions on Industry Applications,1987,23(2):327-333.
[8]Sebastian T,Slemon G R.Transient torque and short circuit capabilities of variable speed permanent magnet motors[J].IEEE Transactions on Magnetics,1987,23(5):3619-3621.
[9]Slemon G R.On the design of high-performance surface-mounted PM motors[J].IEEE Transactions on Industry Applications,1994,30(1):134-140.
