一种小型风电机组的优化最大功率点跟踪控制算法*

黄锦成， 杨 苹

(华南理工大学电力学院，广东省绿色能源技术重点实验室，广东广州 510640)

0 引言

随着社会的进步及科学技术的发展，人类对能源的需求日益增大，而传统能源的过度开发会引起温室效应等一系列问题。风能作为一种可再生清洁能源受到广泛重视，小型风电系统作为风电行业发展的一个分支，日益受到关注［1-2］。但是风能的能量密度低且具有随机性、不稳定性和分布不均匀等特性，给风能的利用带来了许多问题。因此，研究最大功率跟踪技术，提高风力发电系统的风能转换率有着重要的意义。针对如何提高风能转换效率的问题，文献［3］提出根据测风装置检测到的风速，计算风力机的给定功率，再进行最佳叶尖速比控制。该方法需安装测风装置，这样导致系统的造价增加，同时由于风的随机性和波动性，要实现风速的精确测量较难。传统的定步长扰动最大功率跟踪(Maximum Power Point Fracking，MPPT)控制算法是:给控制量一个扰动，根据输出功率的变化来改变扰动的方向，使风力机的输出功率趋近最佳功率负载线。但是风速往往变化较快，该定步长扰动方法的调节速度往往滞后于风速的变化速度，难以使风力机的输出功率趋近最佳功率负载线。本文提出一种优化MPPT控制算法。以小型风力发电机中永磁同步发电机的输出P-ω特性曲线上各点斜率来确定占空比的扰动步长，通过模糊控制来对最大功率点进行跟踪，增强搜索的快速性和稳定性。通过在MATLAB/Simulink中搭建小型风力发电仿真系统，验证本文优化MPPT算法，并与定步长扰动法相比。仿真结果表明:该算法对小型风力发电机组最大功率的跟踪更具实时性，可以提高系统快速跟踪风速变化的能力，而且可以有效降低小型风力发电机输出功率在最大功率点附近的振荡现象，提高小型风力发电机组的风能转换效率。

1 小型风力发电机组动态模型

小型风力发电系统的结构如图1所示。

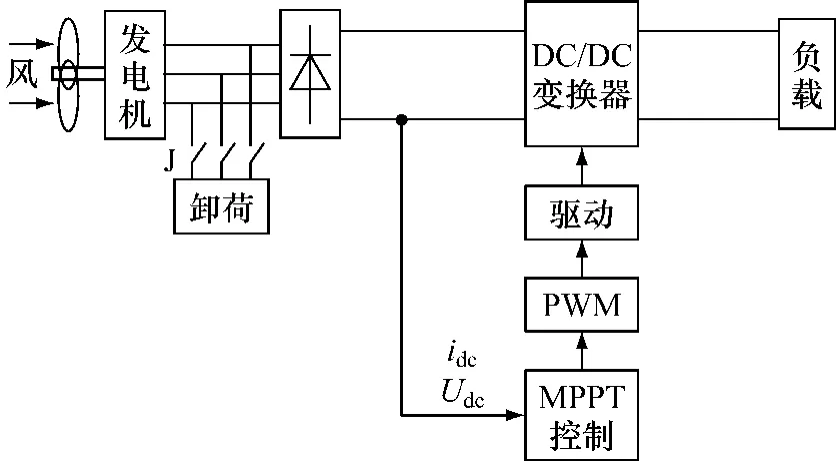
图1 风力发电系统结构图

根据风力机的空气动力学相关知识［6］，风力机输出机械功率Pm可表示为

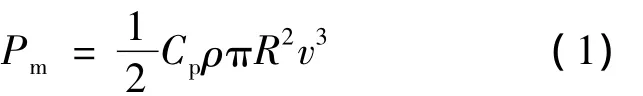
式中:Cp——风能利用系数;

R——风轮半径;

ρ——空气密度;

v——风速。

风力机与永磁同步发电机直接同轴联接，发电机的角速度ω与风力机的角速度ωm相等。根据式(1)，计算风力机输出机械转矩，即永磁同步发电机的输入机械转矩为

在忽略摩擦阻力的条件下，永磁同步发电机的转子运动方程［7］为

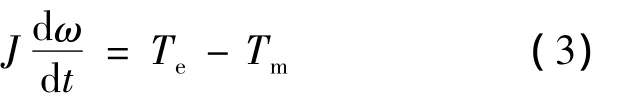
式中:J——转动惯量;

Te——发电机的电磁转矩。

在dq坐标系下，永磁发电机电磁转矩方程为

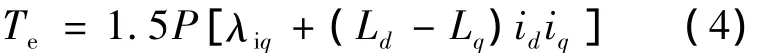
式中:P——极对数;

λ——磁链;

Ld、Lq——定子绕组的 d、q 轴电感;id、iq——dq 轴坐标系电流。

永磁同步发电机a相电流方程为

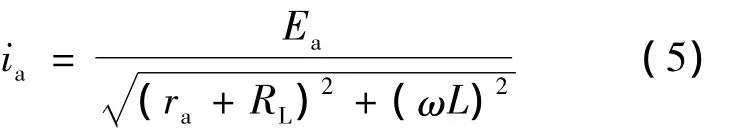
发电机的等效负载电阻为［8］

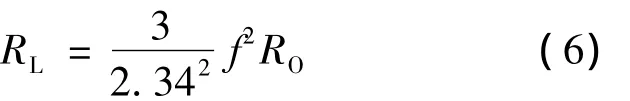
式中:Ea——a相电动势;

ra——定子等效电阻;

L——定子等效电感;

f——由DC/DC斩波电路占空比决定，f与占空比D成反比关系;

RO——负载电阻。

综合分析式(1)～(6)，通过控制DC/DC斩波电路的占空比D，改变发电机等效负载，从而改变发电机的转速，控制发电机的输出功率，使发电机工作在最大功率输出状态。

2 优化MPPT控制算法

针对定步长MPPT扰动观测法的跟踪速度和稳定性的矛盾，将变步长扰动的方法应用于小型风力发电机，以小型风力发电机的P-ω输出特性曲线的斜率来确定占空比的扰动步长，通过模糊控制来对最大功率点进行跟踪，并以DC/DC斩波电路的占空比步长为输出量对小型风力发电机实施MPPT控制。

2.1 优化MPPT控制算法设计思路

2.1.1 MPPT的定步长扰动观测法

传统定步长MPPT算法就是定时对发电机的转速控制指令值施加一定的转速扰动值进行扰动，然后观察发电机的功率变化。若发电机功率增加，那么发电机转速的扰动方向不变;若发电机功率减小，那么将发电机转速的扰动反向。

对于小型风力发电机组而言，定步长MPPT控制算法有以下缺点:①固定转速变化步长，使最大功率点搜索的快速性和稳定性相矛盾;②固定转速扰动，会产生阶梯状变化的发电机转速变化指令，使小型风力发电机的转速不稳定。

2.1.2 MPPT的变步长扰动观测法

定步长扰动观测法可以通过变化固定步长来调节小型风力发电机的输出功率。通过减小ΔD可以改善小型风力发电机在最大功率点附近的功率振荡现象，但较小的ΔD会降低对风速的响应速度;通过增大ΔD可以提高搜索速度，但是较大的ΔD会使最大功率点的功率振荡现象增强。为了克服定步长扰动观测法的上述不足，本文提出了一种变步长扰动观测法。

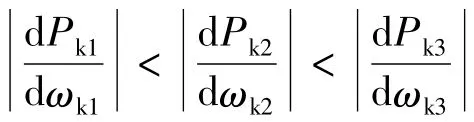
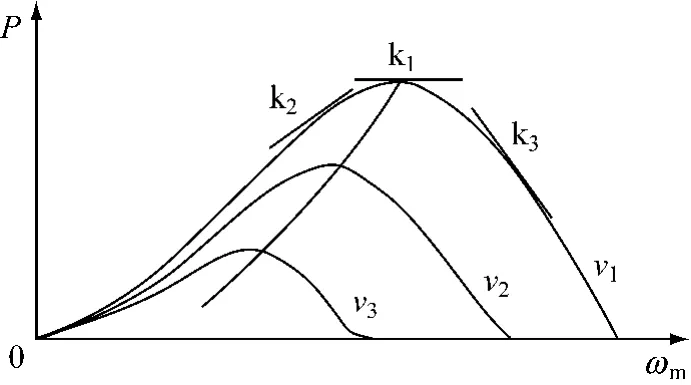
图2 小型风力发电机输出P-ω特性曲线

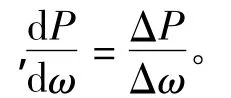
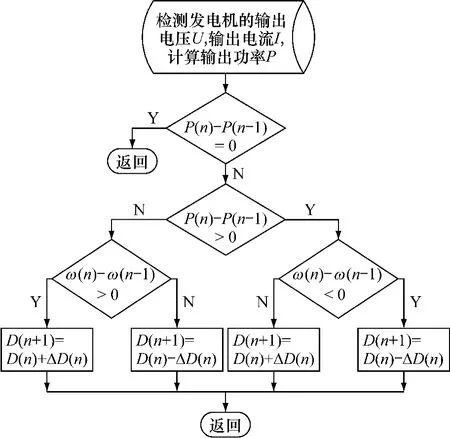
图3 变步长扰动控制流程图

2.2 模糊控制设计

模糊逻辑控制理论在很多工业控制中得到应用，尤其是数学模型不确定，输入变量多，外界影响因素多的系统。因风速的随机性和系统的耦合性，将模糊逻辑控制理论应用到小型风力发电系统中是较好的选择。小型风力发电机的变步长扰动MPPT控制的设计如下。

(1)输入量与输出量的模糊子集与论域。

由于最大功率点处P-ω曲线的斜率Kk1=0，所以模糊控制器的输入e=K(n)-Kk1=K(n)。第n时刻输出量为占空比步长ΔD(n)。将K(n)和ΔD(n)的实际值量化并映射到模糊集合论域EK和EΔD。将模糊集合论域分别定义5个模糊子集，即:

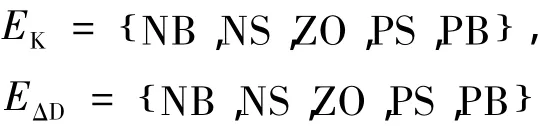
其中 NB，NS，ZO，PS，PB 分别表示负大，负小，零，正小，正大等模糊概念。将模糊集合论域EK和EΔD划分为7个和9个等级，采用离散化的数字集合表示如下:

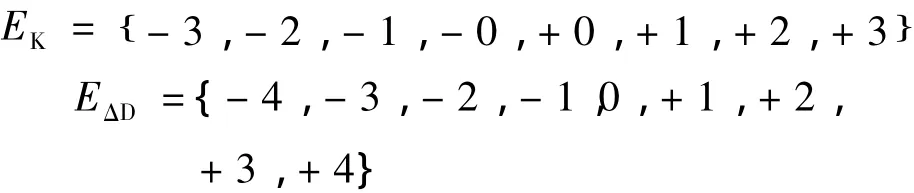
(2)隶属度函数。根据P-ω曲线的特点，选择三角形作为隶属度函数的形状，EK和EΔD的隶属度函数如图4、5所示。

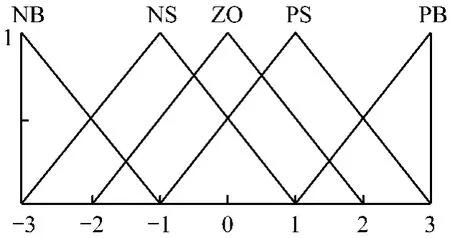
图4 EK的隶属度函数

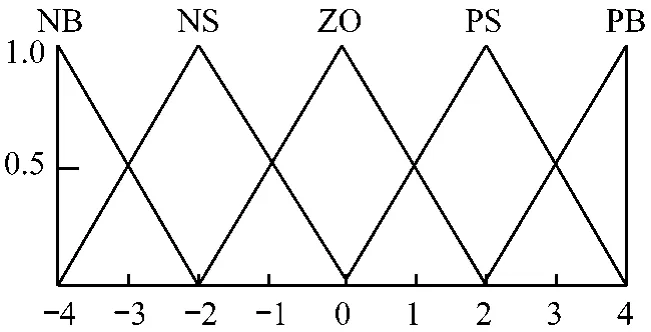
图5 EΔD的隶属度函数

(3)模糊决策表。小型风力发电机输出P-ω特性曲线，可以得到如下原则:

若K(n)的值减小，则继续向原步长调整，否则取相反的方向。离最大功率点较远处，采用较大步长以加快跟踪速度;在最大功率点附近，采用较小的步长，减少搜索损失。

根据上述原则，应用IF A THEN B模糊规则，可以得到模糊规范为:

① If K(n)=NB then ΔD=PB;② If K(n)=NS then ΔD=PS;③ If K(n)=ZO then ΔD=ZO;④ If K(n)=PS then ΔD=NS;⑤ If K(n)=PB then ΔD=NB。最后得到模糊关系R如下。

模糊控制器的输入e=K(n)-Kk1=K(n)，利用模糊关系R，可以得到模糊控制器的输出为ΔD(n)=K(n)·R，而占空比的输出为D(n)=D(n-1)±ΔD(n)。采用隶属度最大原则，可以对输出量ΔD实施反模糊化，根据输入量K(n)的值，占空比D实时改变，对最大功率点进行跟踪。

3 仿真分析

3.1 仿真原理图

优化MPPT控制算法仿真原理图如图6所示。整个仿真模型包括了风力机、发电机、MPPT控制器、DC/DC斩波电路等子模块。其中风力机的参数如下:风轮半径R为2 m，空气密度ρ为1.225 kg/m3，风速为 V，单位 m/s。

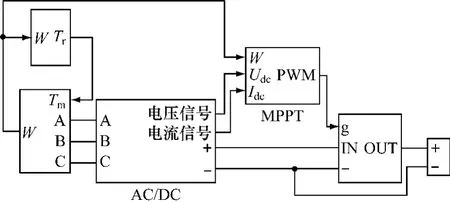
图6 优化MPPT控制算法仿真原理图

3.2 仿真试验结果与分析

当初始风速为12 m/s时，仿真结果如图7所示。

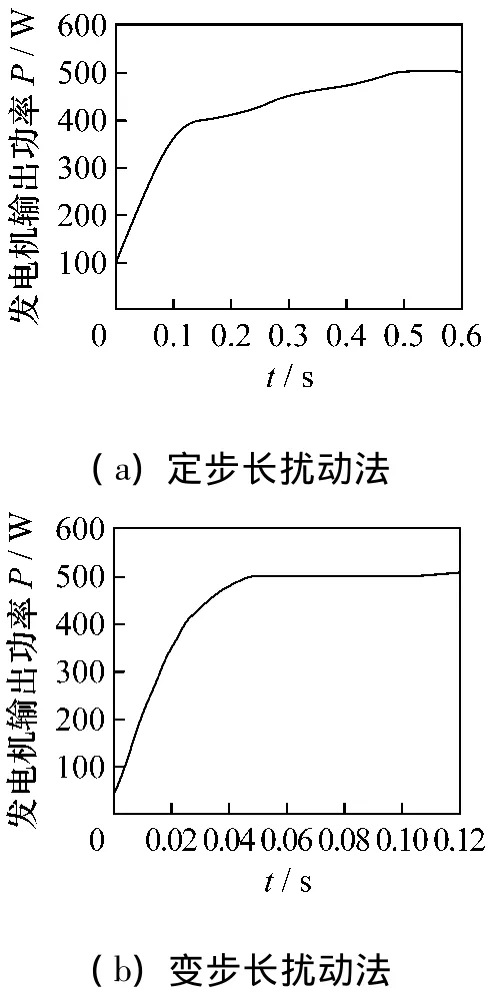
图7 固定风速下的仿真结果

由图7可以看出变步长扰动法达到稳态误差允许范围内的时间在0.05 s，而定步长扰动法达到稳态误差允许范围内的时间则是0.5 s。因此，前者的跟踪速度快于定步长扰动法。

当风速在80 ms内从14 m/s下降至8 m/s的情况下，功率波形图如图8所示。从图中可以看出风速从14 m/s下降至8 m/s时，变步长扰动法能够在0.1 s内跟踪到最大功率点，而且在最大功率点附近变步长扰动法的功率振荡现象比定步长要小。

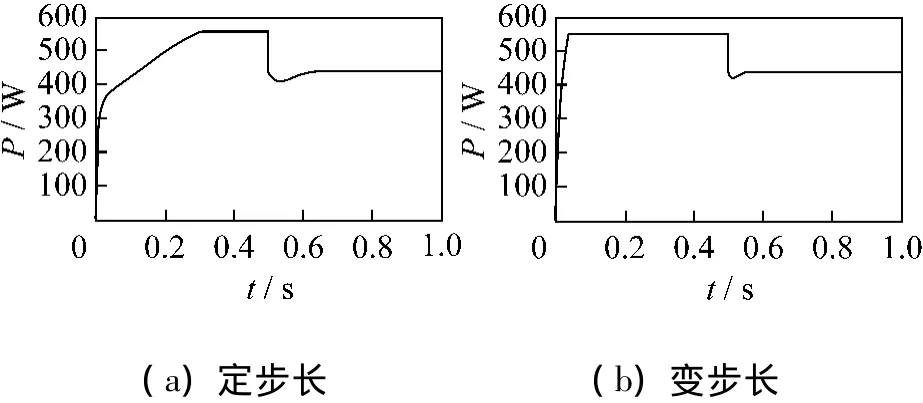
图8 变化风速下的仿真结果

4 结 语

本文在对小型风力发电系统模型进行分析的基础上，结合模糊控制策略，提出一种优化变步长扰动MPPT控制算法。利用MATLAB进行了仿真验证，且在相同条件下与定步长扰动观测法相比较，验证结果表明该算法在各种风速变化情况下均能迅速稳定地重新输出最大功率，有效地解决MPPT控制中快速性和稳定性的矛盾，提高了小型风力发电机组的风能转换效率。

［1］李永东，苑国锋.中国风力发电的发展现状和前景［J］.电气时代，2006(3):16-20.

［2］张明锋，邓凯，陈波，等.中国风电产业现状与发展［J］.机电工程，2010，27(1):1-14.

［3］许洪华，倪受元.独立运行风电机组的最佳叶尖速比控制［J］. 太阳能学报，1998，19(1):30-35.

［4］房泽平，王铁生.小型风电系统变步长扰动MPPT仿真控制研究［J］.计算机仿真，2007，24(9):241-244.

［5］房泽平.独立运行小型风力发电系统功率控制技术研究［D］.内蒙古:内蒙古工业大学，2007.

［6］叶杭冶.风力发电机组的控制技术［M］.北京:机械工业出版社，2002.

［7］唐任远.现代永磁电机理论与设计［M］.北京:机械工业出版社，1997.

［8］陈坚.电力电子变换和控制技术［M］.北京:高等教育出版社，2002.

［9］贾要勤，曹秉刚，杨仲庆.风力发电的MPPT快速响应控制方法［J］.太阳能学报，2004，25(2):171-176.

［10］夏晓敏，王坤琳，吴必军.小型风电系统MPPT模糊/PID控制仿真研究［J］.能源工程，2010(1):26-31.