临界滑水速度的计算研究

李 强，张 卓，张 立

（重庆交通大学土木建筑学院，重庆 400074）

临界滑水速度的计算研究

李 强，张 卓，张 立

（重庆交通大学土木建筑学院，重庆 400074）

利用动量定理，分别计算楔角较小（楔角小于0.4°）和楔角较大两种情况下滑水速度值。以小轿车、中型汽车和载重车为例分析车轮内压、水膜厚度与滑水速度的关系。结果表明:不论楔角较小或者较大，滑水速度与车轮内压成正比;楔角较大且车轮内压一定时，滑水速度与水膜厚度成反比。通过NASA滑水速度方程，对理论计算的滑水速度值进行验证，得出它的可靠性满足要求。

滑水;水膜厚度;临界滑水速度;动水压力

轮胎的滑水现象，也称为水漂现象或者液面效应，是指汽车在路表覆盖有一层水膜的路面上行驶时，因轮胎不能完全排除或无法排除路面水膜，从而出现汽车在水膜上行驶的现象。若路表面水膜对车轮向上的作用力等于车轮自重时，车辆就会处于临界滑水状态，此时所对应的车速为临界滑水速度（简称滑水速度）。

车辆的行驶速度超过其滑水速度，就会使车辆与地面逐步脱离，给行驶中的车辆带来不利的影响。如果水膜对车轮向上的作用力等于车轮重，就会使车辆发生临界滑水状态，此时车速处于临界滑水速度，若车辆运行车速大于滑水速度，就会导致车辆发生侧滑的危险。其原因一方面是是被水膜覆盖的道路表面的抗滑性能大大减小;另一方面是我国干线公路沥青路面的抗滑能力普遍达不到要求［1］，摩擦系数摆值F＜40的路段占50%以上，表面构造深度TD＜0.3 mm的占70%多。降雨后，抗滑能力更低，因此，雨天的交通事故比较多，造成的人员伤亡和经济损失都比较大。Khan（1994），等［2］研究认为，雨天在道路上行驶，由于路面上有水，安全问题变得更加重要。即使是技术熟练小心谨慎的司机，当路面上有水时，高速行驶也难以控制车辆，因为水膜导致摩擦力降低，甚至轮胎与路面完全分离（即发生滑水，也可称为水漂）。董斌［3］从设计的角度综合道路纵坡、圆曲线半径和路面附着系数对停车视距及弯道车速的影响进行分析，提出雨天高速公路纵坡停车视距和安全车速建议修正值。

1 滑水速度计算

1.1 滑水速度计算简介

目前国内外关于滑水速度的计算分为2大类:①是通过水力学理论计算滑水速度;②是通过数值法建立滑水速度计算模型。在理论方面国内外的主要研究主要是针对影响动水压力的因素，如路面粗糙度、车速、车重和水膜厚度以及轮胎花纹形式等，运用水力学和有限元的方法分析动水压力和其影响因素之间的关系，进而求出各个因素对滑水速度的影响规律。栾锡富［4］应用伯努利定理，得出动水压力的公式，并求出处于临界滑水时的公式，据此以ADAMS软件为平台，创建了滑水现象的动态仿真模型，通过仿真实验，得到了大量的动态参数，实现了用计算机仿真实验代替具有破坏性物理实验的方法;同济大学的李少波，等［5］应用伯努利定理计算得到了理想状态发生滑水的临界滑水速度计算式;J.R.Cho［6］根据一般耦合有限体积法和显式有限元方法提出了稳定和可靠的数值过程，模拟和研究轮胎滑水现象。通过三维图案模型可以准确的描述雨水流流经轮胎的过程，使用正交异性壳元素和惩罚Moonley-Rivlin模型有效的模拟复杂轮胎材料组成，并在随后的数值模拟实验中得出了滑水速度和动水压力成正比例关系。

当轮胎与路面接触区域之间的积水能够在加载时间内排出，不会影响到车辆的正常行驶，则被认为不发生滑水，反之则有发生滑水的可能性。车辆发生滑水时，车轮与路面之间形成的楔角是形成车辆滑水的重要条件，而楔角是描述楔段的重要参数，楔角在0.4°时对于车辆发生滑水现象影响显著［7］，故本文分析楔角较小（小于 0.4°）和楔角较大（大于或等于0.4°）2种情况下车辆的滑水速度。

1.2 楔角不同时滑水速度计算

1.2.1 楔角较小时滑水速度计算

当路表积水进入车轮与路面间的空隙时，由于水膜对车轮的向上的动水压力使车轮与路面形成一定的楔角，在楔角较小时，对此时车轮进行受力分析，如图1车轮在前进过程中受到前方水膜对其向上的托力WV及阻力WH，还受到地面对它的支撑力N及附着力f以及自重G。假设路面积水在车轮作用下，即保持着液体保持着理想状态，路面积水不可压缩，路面对液体的水平剪切力和车轮与路面间的附着力f忽略不计。

车辆在有积水的路面行驶时，车轮必定会对路面积水产生挠动，从而引起水膜发生流动，其实质是水膜内流束发生流动。由于流束受到轮胎的阻碍使得流速在轮胎表面接触点变为0，此点即为停滞点，这一过程的发生在轮胎的接地长度范围内，并且流束能量随着流速变化而转化（从动能演化为压能），当流速到达停滞点时，其能量由原先的动能完全转化为压能，也就是动水压力达到最大值。路面流束在界面上的流线如图2［8］。

假设流束在接地范围内的变化符合线性变化规律，即:

式中:v0为汽车速度，km/h;l为轮胎接地长度为，m。

根据力的作用是相互的，轮胎对水膜的作用力FX等于路表面水膜对轮胎的水平作用力WH，因此楔角较小时，沿水平方向的动量定理有（假设路面对车轮的阻力不计）:

式中:mw为水膜的质量，kg。

将式（1）代入式（2），并经过变换得:

式中:ρ为水膜的密度，1 000 kg/N;w为车轮的宽度，m;h为水膜的厚度，m。

路面与轮胎的接地面积为:

式中:G为车轮重力，N;P为车轮内压，kPa。

轮胎与地的接地长度为:

将式（5）代入式（6）可得:

再将式（7）代入式（4），可得:

式中:α为楔角。

将式（8）～式（11）变换得:

当水膜对车轮向上的作用力等于车轮自重（WV=G）时，车辆刚好处于临界滑水状态，此时车速VK为滑水速度，令WV=G，结合式（9）得:

式中:VK为临界滑水速度，km/h。

由式（13）可以看出，楔角较小时，滑水速度和车轮内压、接地长度相关，其它因素（如水膜厚度）对其不存在影响。

1.2.2 楔角较大时滑水速度计算

当楔角较大时，由于水膜水膜对车轮的向上作用力（动水压力）更大，若车轮重一定，则动水压力大于车轮自重，车辆很容易发生滑水现象，对轮胎表面进行受力分析，沿x方向利用动量定理得:

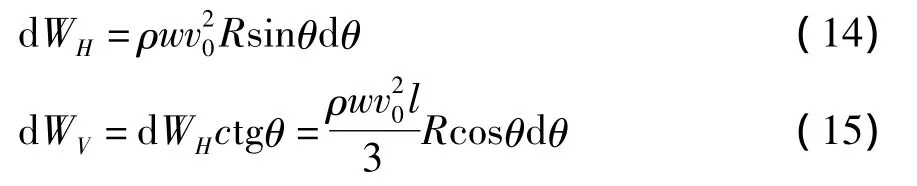
式中:θ为楔角。

对式（15）积分可得:

式中:H为水膜厚度，m;R为车轮半径，m。

当WV=G时，车辆处于临界滑水状态，代入式（16）可得临界滑水速度为:

从式（17）可以看出，水膜较厚时，滑水速度和车轮内压、车轮半径和水膜厚度相关。

1.3 对滑水速度的修正

在正常条件下，车轮通常在轮胎胎面接地压力中心处发生滑水，轮胎胎面接地压力在中心部位最大压力Pmax，一般约为轮胎内压力P的1.55倍，即:

将式（13）、式（17）和式（18）变化得:

式（19）和式（20）分别对应于楔角较小和楔角较大情况

2 滑水速度的分析

通过滑水速度计算公式（19）和（20）可知滑水速度和车轮内压和接地长度、水膜厚度、车轮半径的关系，其中不论楔角大小如何，滑水速度总与车轮内压密切相关。现分析楔角较小和较大2种情况探讨车轮内压、水膜厚度与滑水速度的关系:

1）楔角较小

楔角较小时，滑水速度和车轮内压和接地长度等因素相关，可以通过不同的车型得出车轮内压和滑水速度关系。现分别取小轿车（轮胎型号为185/70R13 86T）、中型汽车（轮胎型号为195/75R16）、载重汽车（轮胎型号为9.00R20），其内压分别是270，375，810 kPa，利用式（18）得出图 3。

图3 楔角较小时车轮内压和滑水速度的关系Fig.3 The relationship diagram of wheels pressure and water-sking speed in the case of small wedge angle

图3反映了楔角较小时车轮内压和滑水速度的关系，滑水速度随着车轮内压增大而增大。例如如果设计车速是120 km/h，小轿车和中型汽车的滑水速度（分别为 70.6、84.9 km/h）都小于120 km/h，对于车辆行驶而言是很不安全的，小轿车和中型汽车在潮湿的路面上的运行速度就不能按照在干燥的路面上行驶，而应该按潮湿路面所要求的车速行驶。

2）楔角较大

①车轮内压和滑水速度关系。楔角较大时，车辆的滑水速度和水膜厚度、车轮半径以及车轮内压相关。现利用在一定水膜厚度基础上，得出车轮内压和滑水速度的关系。假设水膜厚度为7 mm、取小轿车、中型汽车、载重汽车3种车型（型号同上），通过式（20）得出图4。

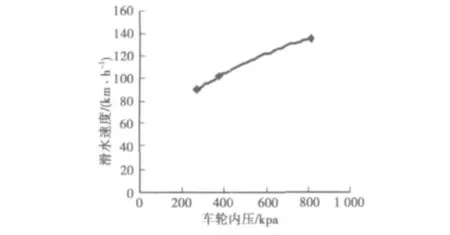
图4 水膜厚度一定时车轮内压和滑水速度的关系图方法Fig.4 The relationship diagram of wheels pressure and water-sking speed in the case of specifc water film

从图4可以看出水膜厚度一定时，滑水速度随着车轮内压增大而增大。如果设计速度为120 km/h，此时小轿车和中型汽车的滑水速度（分别为90.1，101.7 km/h）都小于120 km/h，说明无论是楔角较小或者较大，在潮湿的路面上容易发生滑水的车型多是小轿车中型汽车。这是由于小轿车和中型汽车的内压比较小，而水膜厚度是一定的，若水膜对车轮的作用力也是一定的，这2种车型对水膜的挤压力和水膜对车轮作用力达到平衡后，车辆就会发生滑水现象，若车辆依旧保持原有的大于滑水速度行驶时，此时车辆就有可能出现滑水现象。另外，同种车型在楔角较小时的滑水速度值小于在楔角较大时的值，如小轿车和中型汽车的滑水速度在楔角较小时分别为70.6，84.9 km/h，在楔角较大时分别为 90.1，101.7 km/h。这是由于楔角越大，轮胎的排水速度越快，残留在车轮表面的水分越少，这些水分对车轮的动水压力值越容易和车轮自重越难达平衡，滑水速度就越大，反之，则情况相反。

②水膜厚度和滑水速度关系。持续的降雨落在路表面后，在路表面会形成一层积水，然后这层积水通过以下方式流出到道路外:一是沿着道路横坡被流到路面以外的排水沟;二是通过路表面的“缝隙”下渗到路面的排水层，接着沿着排水路径流出到路面外;停留在路面上的积水则积聚在道路表面形成一层水膜，车辆沿着这层水膜行驶，就会出现滑水现象可能，水膜对车轮向上的作用力取决于楔角、水膜厚度的大小和车轮对水膜的挤压力，故滑水速度的出现和楔角、水膜厚度是分不开的。又根据式（20）知，在楔角较大时，滑水速度和水膜厚度相关，故利用式（20）得出在车轮内压一定的基础上水膜厚度和滑水速度关系。现假设车轮内压为270 kPa，计算结果如图5。

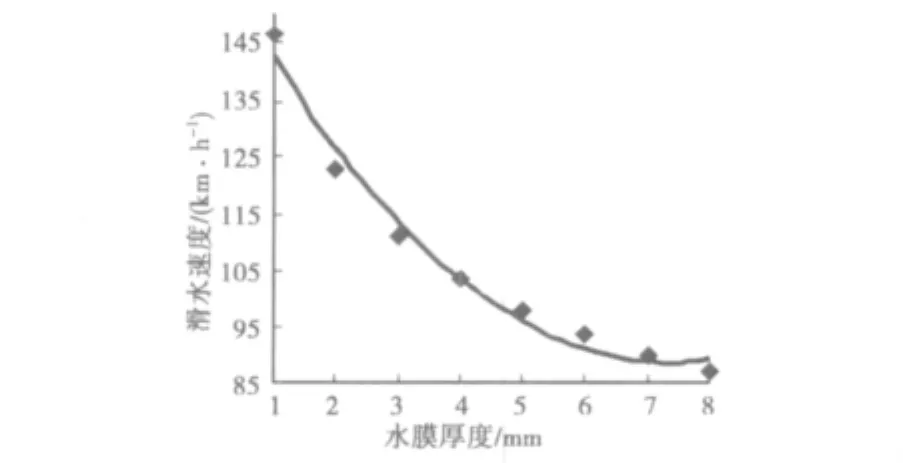
图5 车轮内压一定时水膜厚度和滑水速度的关系Fig.5 The relationship diagram of water thickness and water-sking speed in the case of specific wheels pressure

图5反映了车轮内压一定时水膜厚度和滑水速度的关系，滑水速度随着水膜厚度增加而减小。车辆之所以能在路面上高速行驶主要是因为车辆和路面有接触，车轮不断克服路面对其产生的摩擦力而不断向前滚动。但是若水膜较厚和车速较高，车轮需要在很短时间内克服路面积水对其产生的动水压力，才能与路面接触，这个不断克服动水压力的过程要求车轮在极短时间内将与之接触的积水排走，而随着水膜厚度较大，车轮向外需要排除的水的数量就增多，这就客观增加了车轮的排水难度，残留在轮胎表面的水膜数量越多，这些水分对车轮的动水压力值越容易和车轮自重达到平衡，滑水速度就越小。

3 滑水速度的验证

Horne和 Dreher［9］于1963年测得的滑水速度的试验数据验证模型。试验条件是:ASTM E524标准光滑轮胎，胎压为165.5 kPa，轮荷载为4 800 N，水膜厚度为7.62 mm。并根据实验结果得出了滑水速度和车轮内压之间的关系，就是著名的NASA滑水方程，如式（21）:

式中:V为开始产生滑溜现象的危险车速，km/h;P为轮胎气压，kPa。

利用式（20）所计算得到滑水速度值（简称理论值）与NASA方程所计算得到的滑水速度进行对比，来验证理论滑水速度可靠性，对比结果如图6。

图6反映了理论计算值和NASA计算值的关系对比结果（黑点趋势线是理论计算值，红点趋势线是NASA计算值），从图中可以看出滑水速度随着车轮内压的增大而增大，但是对于相同的车轮内压，理论所得出的滑水速度值略大于NASA滑水方程所计算的滑水速度值，但二者相差不大（只有4%差异），说明理论滑水速度值可靠性满足要求。

图6 理论计算值和NASA计算值的关系对比Fig.6 Comparision figure of theoretical value and NASA value

4 结语

通过滑水现象的分析，得出滑水速度是引起交通事故的重要因素，并分析了滑水速度产生的条件是楔角、水膜厚度和车速，原因是车轮对水膜的挤压和水膜对车轮的作用力的平衡性导致的，利用动水压力计算得到了楔角较小和较大时滑水速度计算值，分析了水膜厚度、车轮内压和滑水速度之间关系，并利用NASA滑水方程对理论计算滑水速度值进行验证，得出以下结论:

1）不论楔角较小或者较大，滑水速度随着车轮内压成正比。在潮湿路面上发生滑水的车型多是小轿车和中型汽车。

2）楔角较大且车轮内压一定时，滑水速度随着水膜厚度成反比。

3）通过NASA滑水方程与本文所得到的理论滑水速度值进行比对，得出二者相差4%，说明理论滑水速度值可靠性满足要求。

（References）:

［1］ 季天剑.降雨对轮胎与路面附着系数的影响［D］.南京:东南大学，2004.

［2］ Khan A M，Bacchus A，Holtz N M.Multilane highway design crossfall and drainage issues［J］.Transportation Research Record，1994，1471（1）:1-9.

［3］ 董斌.部分滑水条件下高速公路车辆行驶安全研究［D］.重庆:重庆交通大学，2011.

［4］ 栾锡富，周俊.滑水现象的ADAMS仿真［J］.佳木斯大学学报:自然科学版，2006，24（3）:388-389.

LUAN Xi-fu，ZHOU Jun.ADAMS simulation of water-skiing phenomenon［J］.Journal of Jiamusi University:Natural Science，2006，24（3）:388-389.

［5］ 李少波，张宏超.动水压力的形成与模拟测量［J］.同济大学学报:自然科学版，2007，35（7）:915-918.

LI Shao-bo，ZHANG Hong-chao.Hydrodynamic pressure of the analog measurements［J］.Journals of Tongji University:Natural Science，2007，35（7）:915-918.

［6］ Cho J R，Lee H W，Sohn J S.Numerical investigation of hydroplaning characteristics of three dimension patterned tire［J］.European Journal of Mechanics A/solids，2006，25（6）:914-926.

［7］ 朱永刚.考虑动压及路面粗糙度时轮胎湿牵引性能［J］.汽车工程，2007，29（7）:616-629.

ZHU Yong-gang.A study on tire wet traction performance with consideration of road roughness and hydrodynamic action［J］.Automotive Enginee-ring，2007，29（7）:616-629.

［8］ 余治国，李曙林.机轮动力滑水机理分析［J］.空军工程大学学报:自然科学版，2004，5（5）:9-11.

YU Zhi-guo，LI Shu-lin.Mechanism of wheel power water-sking［J］.Journals of Air Force Engineering University:Natural Science，2004，5（5）:9-11.

［9］ Horne W B.Tire hydroplaning and its effects on tire traction［J］.Highway Research Record，1968，214:24-33.

Calculation and Research of Hydroplaning Critical Velocity

LI Qiang，ZHANG ZHuo，ZHANG Li
（School of Civil＆ Architectual Engineering，Chongqing Jiaotong University，Chongqing 400074，China）

The paper which made use of wedge angle of momentum caculated hydroplaning critical velocity in both cases which consists of small wedge angle（＜0.4°）and larger wedge angle.Analysis of the relationship between wheel pressure，water film thickness and hydroplaning critical velocity with the exam of cars，medium cars and trucks.The results showed that:no matter small or large wedge angle，water skiing and wheel speed directly proportional to internal pressure;wedge angle is larger and the wheel pressure is constant，water-skiing and water film thickness is inversely proportional to the speed.Verifying hydroplaning critical velocity according to NASA skilling speed equation and the result show that its reliability to meet the requirements.

water-skiing;water film;hydroplaning critical velocity;hydrodynamic pressure

U491.2+54

A

1674-0696（2011）05-0989-05

10.3969/j.issn.1674-0696.2011.05.022

2011-05-30;

2011-06-28

重庆市教委科学技术研究项目（KJ100422）

李 强（1983-），男，河南三门峡人，硕士研究生，主要从事不良天气下道路交通安全方面的研究。E-mail:hanbotupian@163.com。