三塔悬索桥静力挠度可靠度分析
2011-06-02刘晓銮
刘晓銮
(同济大学 桥梁工程系,上海 200092)
三塔悬索桥静力挠度可靠度分析
刘晓銮
(同济大学 桥梁工程系,上海 200092)
采用响应面法对三塔悬索桥主梁最大挠度进行静力可靠度分析,考察三塔悬索桥主梁最大挠度对结构材料、几何尺寸及外荷载等不确定因素的变异而发生变化的规律。结果表明:三塔悬索桥主梁最大挠度可靠指标是由单主跨施加活荷载控制的,主缆弹性模量、汽车活荷载、主缆截面面积及中塔弹性模量等对主梁最大挠度的影响最为显著。
悬索桥;挠度;静力可靠度;失效概率;响应面法
传统大跨径悬索桥基本都采用两塔单跨或三跨结构形式,其最大主跨跨径已经接近2 000 m(明石海峡大桥)。三塔悬索桥是在两塔悬索桥主跨的中部增设一座主塔,以减轻主缆和两端锚碇受力的全新结构形式,中主塔在纵向只是一个通过鞍座支承主缆。与两塔悬索桥相比,虽然都以悬索为主要承重结构,但因为多了一个中塔和一个主跨,三塔悬索桥结构受力特征显然不同。由于中塔在纵向只是通过一个鞍座支承主缆,其受到的主缆纵向约束较边塔弱得多,并因此导致结构的整体刚度下降[1]。
国内外已有较多学者对两塔悬索桥做过静力可靠度分析[2-5],但目前对三塔悬索桥的研究还仅限于确定性结构分析。笔者以泰州长江公路大桥为工程背景,应用ANSYS建立了三塔悬索桥的有限元模型,应用响应面法实现了对三塔悬索桥的静力挠度可靠度分析,并进行了静力挠度可靠指标的敏感性因素分析,找到了影响三塔悬索桥静力挠度可靠度的主要随机因素。
1 响应面法
大型桥梁结构由于具有很强的非线性特征,不容易获得其极限状态方程的具体表达式,因而无法直接采用一次二阶矩法(FORM)计算其可靠指标。为了解决这个问题,采用响应面法。响应面法的核心就是采用简单的多项式来表示隐式极限状态方程。笔者采用不含交叉项的二次多项式[6]:
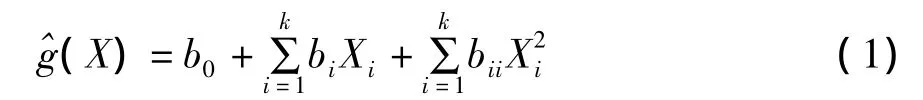
2 应用实例
2.1 实例简介
泰州长江大桥主桥为三塔悬索桥,跨径布置为(390 m+2×1 080 m+390 m),是国内也是世界上首次建造的千米级跨径的三塔悬索桥,其总体布置如图1。2个主跨矢跨比相同,均为1/9,矢高为120 m。主梁采用扁平钢箱梁,中心线处梁高为3.5 m,全宽39.1 m。边塔为混凝土桥塔,塔顶标高180.0 m;中塔为钢塔,塔顶标高200.0 m,顺桥向为人字形,分叉点在主梁以下。

图1 泰州长江大桥总体布置图(单位:m)Fig.1 General view of the Taizhou Bridge
2.2 有限元模型
采用ANSYS软件建立三塔悬索桥的空间有限元模型,如图2。主缆、吊杆采用单向受拉杆单元LINK 10模拟,考虑主缆和吊杆初始应力刚度的影响;主梁、桥塔、横梁用空间梁单元BEAM 4模拟;主梁横隔板和桥面系用集中质量块单元MASS 21模拟。主梁单元和吊杆单元通过刚臂连接。

图2 三塔悬索桥有限元模型Fig.2 FEM model of three-tower suspension bridge
2.3 静力挠度可靠指标计算
参考以往学者对两塔悬索桥的静力挠度可靠度分析成果[3,5],本文假定三塔悬索桥的结构随机变量为主缆、吊杆、主梁、边塔和中塔的弹性模量Ei、截面面积Ai和材料容重ri,主梁、边塔和中塔的截面惯性矩Ii,及汽车活荷载q,其统计特征如表1。对三塔悬索桥来说,一个主跨施加基本活荷载,另一个主跨不加载,是中塔及其上主鞍座设计的控制工况,也是三塔悬索桥设计的最主要控制工况[7]。因此,笔者在对三塔悬索桥进行静力挠度可靠度分析时,考虑2种活荷载加载方式:加载方式①,恒载+活荷载(单主跨加载);加载方式②,恒载+活荷载(双主跨加载)。活荷载以均布荷载的形式施加到主梁单元上[8]。
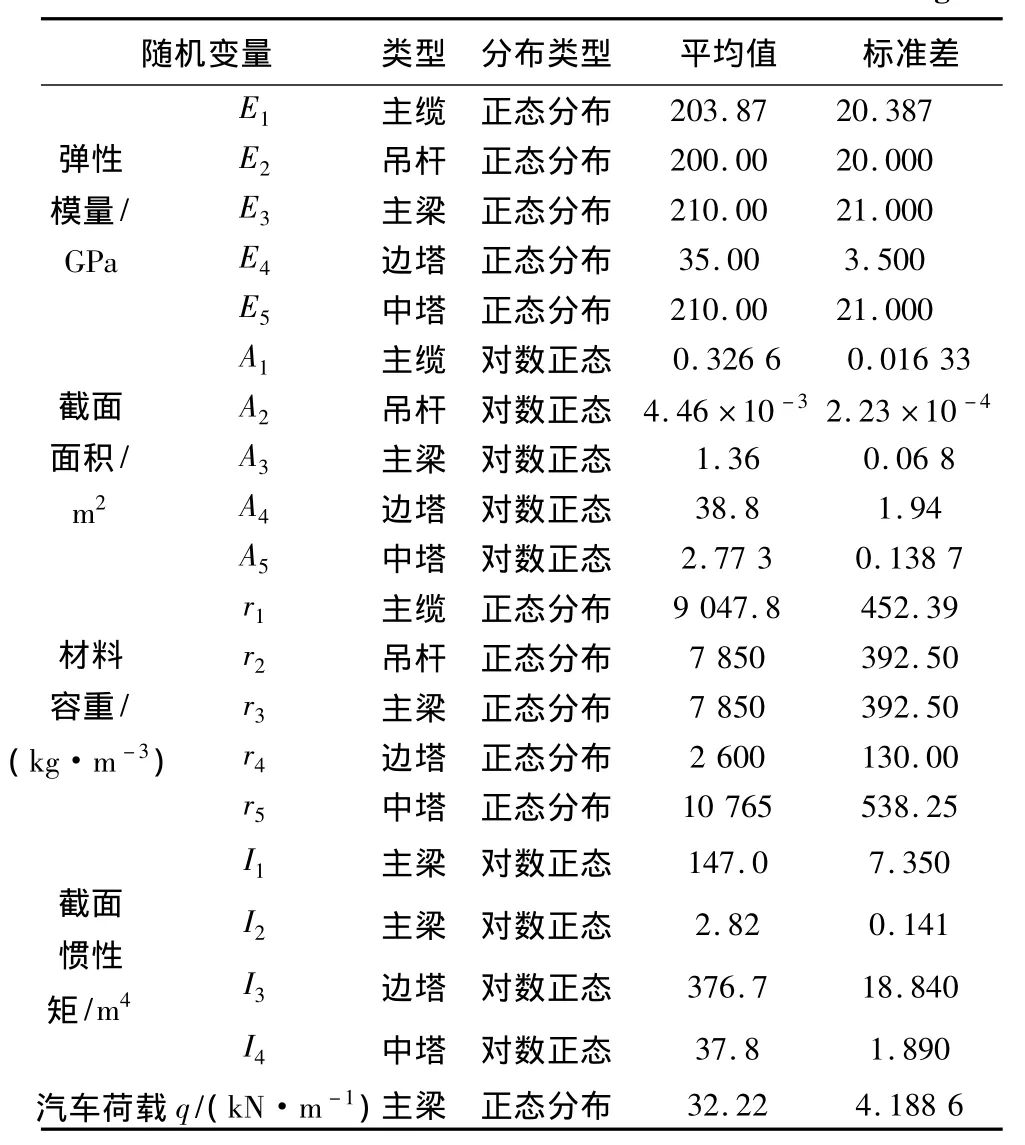
表1 泰州大桥随机输入变量的统计特征Tab.1 Statistics of the random variables for Taizhou Bridge
在对三塔悬索桥进行静力挠度可靠度分析时,关键是确定主梁的容许挠跨比。两塔悬索桥设计的容许挠跨比通常采用L/400,L为主跨跨径。韩大章和华新在对泰州大桥的关键技术问题进行分析时指出,规范制定挠跨比的限值,实质上是为了限定竖向荷载作用下的最大纵坡和梁端竖向转角以保证行车的平顺性,他们根据泰州长江大桥的具体情况,在保障行车平顺的条件下,采用最大容许挠跨比 L/250[1]。由此计算出三塔悬索桥主梁在活荷载作用下的最大竖向挠度[u]=L/250=4.32 m,建立极限状态方程:
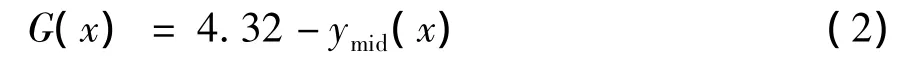
式中:ymid(x)为主梁最大挠度。
采用响应面方程模拟式(2),求解得到加载方式①的静力挠度可靠指标为0.786 2,失效概率为0.215 9;加载方式②的静力挠度可靠指标为2.812 8,失效概率为 2.455 6 ×10-3。由此可见,三塔悬索桥在单主跨加载时的静力挠度可靠指标明显低于双主跨加载时的可靠指标,因此三塔悬索桥的静力挠度可靠度是由单主跨施加活荷载控制的。李扬海,等[9]认为正常使用极限状态的目标可靠指标βT宜限在0.675~1.645之间,由此可见,泰州长江大桥静力挠度满足此目标可靠指标要求。
2.4 可靠指标敏感因素分析
可靠指标对随机变量平均值和标准差的敏感度,其具体计算公式为[10]:

式中:β是可靠指标;αi是第i个随机变量的方向余弦;μi和σi分别是第i个随机变量的平均值和标准差。
敏感度计算结果如图3。
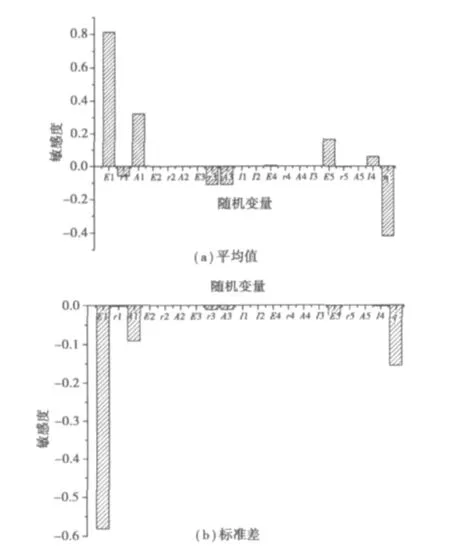
图3 可靠指标对随机变量平均值和标准差的敏感度Fig.3 Sensitivity of reliability index with respect to mean value and standard deviation of random variables
从图3可以看出,三塔悬索桥主梁最大挠度可靠指标β对主缆弹性模量E1的平均值最为敏感,其它依次为汽车活荷载q、主缆截面面积A1、中塔弹性模量E5、主梁材料密度r3、主梁截面面积A3和中塔截面惯性矩I4,对其它随机变量平均值敏感程度较低;可靠指标β对主缆弹性模量E1的标准差最为敏感,对汽车活荷载q和主缆截面面积A1的标准差次之,对其它随机变量标准差的敏感程度较低。
对比三塔悬索桥和两塔悬索桥的静力挠度可靠指标敏感性分析[3,5],发现,两者对主缆弹性模量和截面面积、主梁材料密度和截面面积以及汽车活荷载的敏感程度都比较高,但三塔悬索桥对主缆材料密度的敏感程度要低于两塔悬索桥;另外,三塔悬索桥对中塔弹性模量和截面惯性矩的敏感程度较高,而两塔悬索桥对桥塔弹性模量和材料密度的敏感程度很低。
在确定响应面方程的待定参数后,可依据式(2)计算主梁最大挠度,绘出结果如图4。
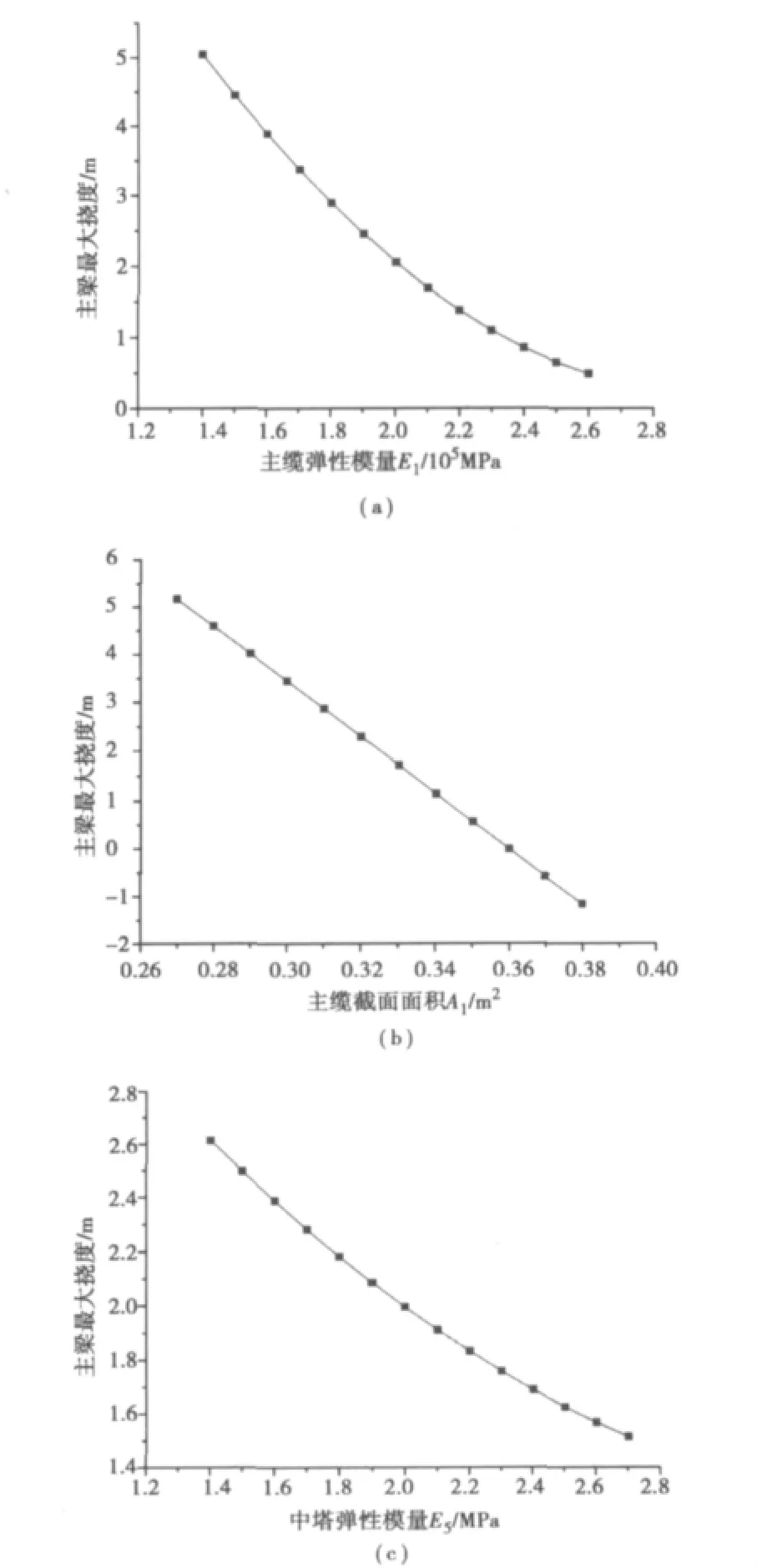
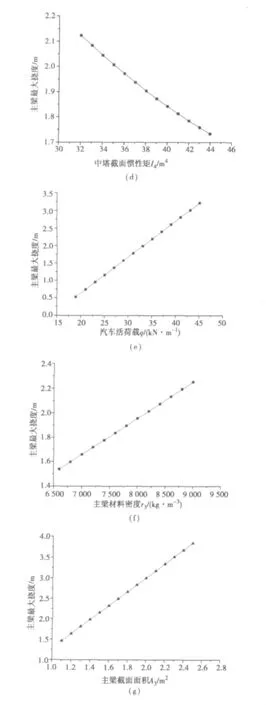
图4 随机变量对主梁最大挠度的影响Fig.4 Influence of random variable on the maximum deflection of stiffened girder
图4中横坐标是在工程应用的±3σ范围内变化[3]。从图4可以看出,三塔悬索桥的主梁最大挠度与主缆弹性模量E1和截面面积A1、中塔弹性模量E1和截面惯性矩I4的变化成反比,与活荷载集度q、主梁材料密度r3和截面面积A3的变化成正比。图中曲线斜率大致反映了各随机变量对主梁最大挠度的影响程度。对比各图可以看出,主缆弹性模量E1和截面面积A1、汽车活荷载q对主梁最大挠度的影响最为显著,与图3得出的结论一致。
3 结论
1)三塔悬索桥在单主跨加载时的静力挠度可靠指标明显低于双主跨加载时的静力挠度可靠指标。因此,三塔悬索桥的静力挠度可靠指标是由单主跨施加活荷载控制的。
2)三塔悬索桥的静力挠度可靠指标对主缆弹性模量的平均值和标准差最为敏感,这与两塔悬索桥相同,但三塔悬索桥对中塔弹性模量和截面惯性矩的敏感程度较高,而两塔悬索桥对桥塔弹性模量和材料密度的敏感程度很低。
3)采用不含交叉项的二次多项式的响应面法求解三塔悬索桥的可靠指标满足工程精度要求,可以用于三塔悬索桥的非线性随机静力分析。
(References):
[1] 韩大章,华新.泰州长江大桥的关键技术问题[J].公路,2008(6):54-58.HAN Da-zhang,HUA Xin.The key technology issues of Taizhou Changjiang Bridge[J].Highway,2008(6):54-58.
[2] Imai K,Frangopol D M.System reliability of suspension bridges[J].Structural Safety,2002(24):219-259.
[3] 石磊,刘春城,张哲,等.大跨悬索桥非线性随机静力分析[J].大连理工大学学报,2004,44(3):421-424.
SHI Lei,LIU Chu-cheng,ZHANG Zhe,et al.Nonlinear stochastic static analysis of long-span suspension bridge[J].Journal of Dalian University of Technology,2004,44(3):421-424.
[4] 郭彤.大跨度悬索桥状态评估实用方法研究与应用[D].南京:东南大学,2005.
[5] 李生勇,张哲.自锚式悬索桥主梁挠度非线性随机静力分析[J].武汉理工大学学报,2010,34(2):266-269.
LI Sheng-yong,ZHANG Zhe.Nonlinear stochastic static analysis for the deflection of main span girder of a self-anchored suspension bridge[J].Journal of Wuhan University of Technology,2010,34(2):266-269.
[6] Bucher C G,Bourgund U.A fast and efficient response surface approach for structural reliability problems[J].Structural Safety,1990,7(1):57-66.
[7] 王忠彬,万田保.泰州长江公路大桥三塔两跨悬索桥结构行为特征[J].桥梁建设,2008(2):38-40.
WANG Zhong-bin,WAN Tian-bao.Structural characteristics of three-tower and two-span suspension bridge of Taizhou Changjiang Highway Bridge[J].Bridge Construction,2008(2):38-40.
[8] 程进,肖汝诚.斜拉桥结构静力可靠度分析[J].同济大学学报:自然科学版,2004,32(12):1593-1598.
CHENG Jin,XIAO Ru-cheng. Static reliability analysis of cablestayed bridges[J]. Journal of Tongji University: Natural Science,2004,32( 12) : 1593 - 1598.
[9] 李扬海,鲍卫刚,郭修武,等. 公路桥梁结构可靠度与概率极限状态设计[M]. 北京: 人民交通出版社,1997.
[10]Hohenbichler M,Rackwitz R. Sensitivity and importance measures in structural reliability[J]. Civil Engineering Systems,1986( 3) :203 - 210.
Static Deflection Reliability Analysis of Three-Tower Suspension Bridge
LIU Xiao-luan
(Department of Bridge Engineering,Tongji University,Shanghai 200092,China)
Static reliability analysis was carried out for the maximum deflection of main girder of three-tower suspension bridge by response surface method(RSM).The law of main girder’s deflection was studied with the variation of structural parameters such as material properties,geometric dimensions and external load,etc.The results demonstrate that the static deflection reliability was controlled by the load case when the live load was uniformly distributed on one central span girder.It was concluded that the variation of modulus of the main cable,the live load,the area of the main cable and the modulus of the central tower had significant effect on the deflection of main girder of three-tower suspension bridge.
suspension bridge;deflection;static reliability;failure probability;response surface method
U442.27
A
1674-0696(2011)05-0895-04
103969/j.issn.1674-0696.2011.05.002
2011-04-25;
2011-05-20
国家自然科学基金资助项目(51008223);上海市浦江人才计划项目(09PJ1409500)
刘晓銮(1982-),男,山东寿光人,博士研究生,主要从事桥梁结构系统可靠度研究。E-mail:lxluan292@163.com。
