拱形减振橡胶垫在荷载作用下的应力分析*
2011-06-02陈玉骥罗旗帜
陈玉骥,罗旗帜,2
(1.佛山科学技术学院土木工程与建筑系,广东佛山 528000;2.湖南大学土木工程学院,湖南长沙 410082)
拱形减振橡胶垫在荷载作用下的应力分析*
陈玉骥1,罗旗帜1,2
(1.佛山科学技术学院土木工程与建筑系,广东佛山 528000;2.湖南大学土木工程学院,湖南长沙 410082)
通过实验确定了橡胶材料的Mooney-Rivlin常数。以拱形减振橡胶垫为对象,建立了空间有限元模型。考虑材料非线性和几何非线性影响以及半球形空腔内的气体压力作用,用有限元法分析了这种减振橡胶垫的应力状态和极限承载力。结果表明,在正常使用下,减振橡胶垫在含半球区域的水平正应力沿着水平方向基本上呈波浪型的变化,沿竖向基本上呈线性分布;剪应力比正应力小一个数量级;无半球区域应力分布比较均匀,变化很小;拱形减振橡胶垫中的半球形空腔的半径R、半球间距L和橡胶垫厚度h对极限承载力均有一定的影响;当R=5.5 mm,L=3 mm,h=14 mm时,拱形橡胶减振垫的极限承载力为375 kN,与正常使用下的荷载之比为3∶ 1;极限状态时拱形橡胶减振垫的厚度约为原始厚度的一半。
减振橡胶垫;超弹性材料;应力;顶面位移;极限承载力
铁道线路上,为使行车平顺,在钢轨和混凝土轨枕之间都设置了减振垫进行隔振或减振。目前应用的减振垫一般为板式橡胶垫和圆柱形橡胶减振垫。前者为实心结构,减振效果欠佳,疲劳性能也不理想;后者存在局部应力集中而发生的撕裂问题。拱形减振橡胶垫是一种新型减振产品(见图1),它是以橡胶为主体,在橡胶垫的底部均匀排列若干个独立,大小相同的半球空心气室,该半球形空腔在工作时所产生的空气压力可以起到气体弹簧的作用,有助于减少振动的传递和冲击。顶部构造能均匀分散所承受的压力,使力沿着半球顶周围向下传递,解决了局部应力集中而发生的撕裂问题,提高了其承载能力和延长其使用寿命。可见,拱形减振橡胶垫是一种较好的铁轨减振装置,具有良好的应用前景。本文根据有限元理论,采用块体单元,考虑橡胶垫的材料非线性和大变形特征,分析了拱形减振橡胶垫的应力状态和极限承载力,讨论了半球空腔的半径、半球间的距离和橡胶垫的厚度对极限承载力的影响,其结果可为拱形减振橡胶垫的推广应用提供参考。
1 拱形减振橡胶垫有限元模型的建立
1.1 橡胶材料的超弹性特征
拱形橡胶垫的橡胶材料是主要的受力材料。橡胶不同于一般的弹性材料,它属于超弹性材料,具有超弹性特征,在较小的外力作用下就能显示出高度的变形能力。而在外力除去后,又能恢复原来的形状,几乎没有永久变形。橡胶的弹性与金属的弹性不同,若将橡胶棒用力拉伸,其最大伸长通常在500%~1000%之间。除在小变形区域外,橡胶没有固定的杨氏模量[1]。
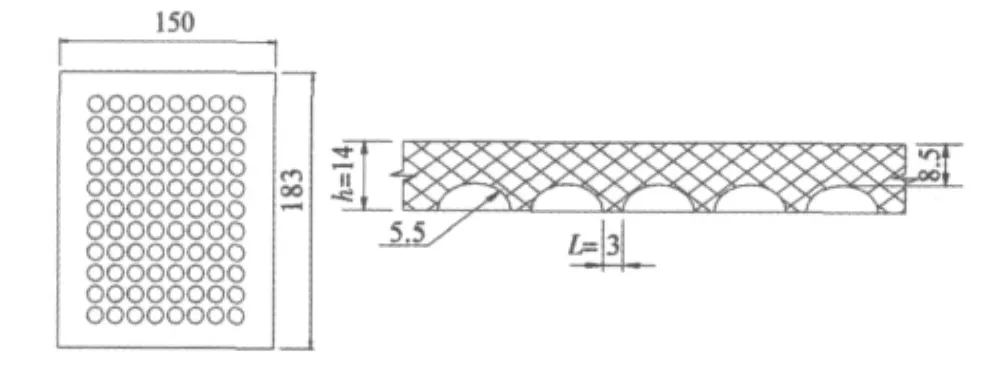
图1 拱形减振橡胶垫的尺寸图Fig.1 The size of the arch decouple rubber bearing
一般工程材料(如金属)的应力应变关系可由一条弹塑性响应曲线来描述,而对于像橡胶这样的超弹性材料,其应力应变关系则需根据应变能函数W来描述,该应变能函数W对应变分量的导数就是相应的应力分量。关于橡胶材料的应变能函数,有不同的模型[2-4]。其中,以唯象理论为基础的理论模型较为合理。这种方法由Mooney于1940年提出,然后Rivlin将其推广到了一种更通用更合理的形式。此理论的基本思想是直接从橡胶材料的大变形现象出发,不考虑具体的微观分子结构,推导出可以完全或比较近似表达橡胶材料的应力应变关系的一种数学格式。
Rivlin指出,对于各向同性材料来说,其材料的对称性对应变能函数的可能形式给予了一定限制;此外,静水压力对橡胶之类的材料基本上是没有压缩的。因此Rivlin假设橡胶材料是不可压缩的,而且在小应变状态下是各向同性的,这种各向同性不可压缩材料的应变能函数W可以用下式表达

式中:I1和I2为应变张量第一和第二不变量;Cij为Mooney-Rivlin常数。
1.2 Mooney-Rivlin常数的确定
Mooney-Rivlin常数是一种适用于不可压缩橡胶类材料的材料常数[5],现行材料手册中通常查不到超弹材料的Mooney-Rivlin常数,但可通过对材料标准试样的实验所得数据来确定这些常数。
本文采用工程软件ANSYS自带的超弹性分析程序进行材料特性拟合计算。在ANSYS中提供了用于模拟橡胶的超弹性材料单元,以及与之相对应的Mooney-Rivlin材料属性。按照式(1)所取的应变能函数的项数不同,提供了若干Mooney-Rivlin材料模型。本文计算采用5常数的Mooney-Rivlin材料计算模型,这5个常数可根据试验数据在ANSYS中计算生成。为此,作者通过对拱形减振橡胶垫取样,并对其进行标准实验[6],测得了在压力作用下的应力应变关系,并将所测得的数据通过ANSYS计算得出应变能函数所需要的常数,从而确定了所用橡胶材料的材料属性。根据实验所得的应力及应变,通过ANSYS的计算,得到了本文所研究的橡胶垫材料由Mooney-Rivlin模型所描述的应力应变关系如图2所示。
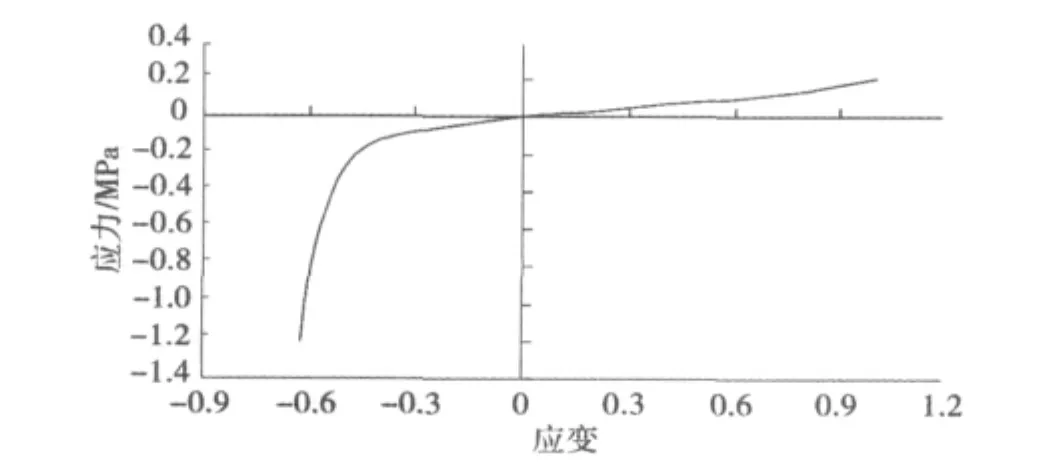
图2 在ANSYS中定义的应力应变曲线Fig.2 Stress- strain curve defined by ANSYS
1.3 减振橡胶垫的有限元计算模型
由于拱形减振橡胶垫具有对称性,包含2个对称轴,故以其1/4进行有限元分析。建模时,采用块体单元,其网格划分模型如图3所示(其中,x为沿短边方向的坐标,y为沿长边方向的坐标)。有限元分析中,打开大变形开关,以反映橡胶的大变形效应。非线性刚度方程的求解,采用增量迭代法计算,其收敛性以位移收敛准则进行控制。
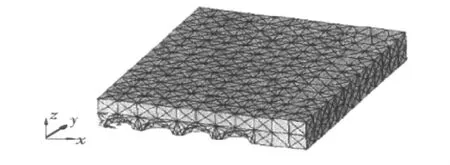
图3 1/4减震橡胶垫有限元离散模型图Fig.3 One-quarter FEM model of the decouple rubber
2 荷载的施加形式
作用于减振橡胶垫的荷载有顶面铁轨所传递的列车轴重荷载以及半球形空腔内部的气体压力荷载。
2.1 正常使用状态
在进行正常使用状态下的应力分析时,轴重荷载采用标准特种荷载,即火车的轴重为250 kN,每个减振橡胶垫上的荷载为250/2=125 kN。计算时,将该荷载均匀分布于减振橡胶垫的顶面,相应的荷载集度为125 kN/(183×150)mm2=4.55 N/mm2。半球形空腔内部的气体压力荷载是由顶面荷载作用使半球形空腔体积发生变化所引起的,它与半球形空腔体积的变化有关,故事先无法知道该气体压力的值。为了得到半球形空腔内气体的压力荷载,需进行试算。为此,先做如下假设:
(1)在施加荷载的过程中,半球形空腔内气体不会漏掉;
(2)半球形空腔内的气体变化为等温变化;
(3)气体的压力随着轴重的增加而线性增加;
(4)半球形空腔内气体的初始压力为标准大气压。
试算时,首先忽略半球形空腔内气体的存在,对减振橡胶垫施加顶面的列车轴重荷载。顶面加载采用分级加载方式,求解过程中考虑橡胶材料的材料非线性和由于大变形引起的几何非线性。然后根据减振橡胶垫在顶面荷载125 kN作用下半球形空腔的变形情况,计算其在变形后的体积,通过与变形前的体积比较,得到此时半球形空腔内气体的压力。
计算表明,整个减振橡胶垫内的所有半球形空腔变化后的形状都很接近,几乎都近似于半椭球形,故为了简化分析,假设所有半球变化后的尺寸都一样,并取平均尺寸进行计算。
根据假设(2),有如下关系:

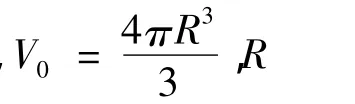

通过上述公式,得到受压变形后半球形空腔内的气体压力p1。在减振橡胶垫未受到顶面荷载时,整个减振橡胶垫边界(包括半球形空腔内壁)都受到一个标准大气压作用,该标准大气压为一平衡力系,故这时的气压不计入荷载,而以后加载时所有气体压力荷载均应以标准大气压为起点开始计算。所以在变形后半球形空腔内的气体压力应该用以下气体压力作为荷载

由于在第1次试算的各级加载时,没有考虑半球形空腔内气体压力的存在,而是在加载达到125 kN后,根据半球形空腔的体积变化反推气体压力。显然,上述分析与加载过中气体压力随半球形空腔体积的变化而改变的实际情况有所不同。所以,为模拟实际情况,应该将第1次试算得到的气体压力p按假定(3)再施加于半球形空腔内表面上,再进行加载计算,即该压力由零开始随轴重的增加而线性增加至(4)式所确定的值。当加载结束后,又可求出新的半球形空腔体积和相应的气体压力。依此循环计算,直到相邻2次计算结果相差较小时即可认为这时的压力为顶面荷载为125 kN时相应的气体压力,经过反复试算,最终得到在顶面荷载为125 kN时半球形空腔内的平均气体压力为0.351个大气压。
2.2 承载力极限状态
为方便起见,计算极限承载力时引入如以下假设:
(1)只考虑到材料的超弹性性质,不考虑到其他的因素,如橡胶材料的疲劳,以及其工作环境对材料的影响。
(2)气体压力在顶面加载过程中逐渐加大(与上面的假设(3)相同),到正常使用荷载时,假设气体压力达到最大值,然后随着顶面荷载的增加,认为出现了气体泄漏现象。当达到极限承载力时,气体正好全部漏完。顶面荷载和气体压力随时间的变化示意图如图4所示(图中t1表示达到正常使用状态所对应的时刻,t2表示达到极限承载力所对应的时刻)。

图4 荷载随时间的变化示意图Fig.4 Sketch map of load - time
3 含半球形空腔的减振橡胶垫的应力状态分析
采用上述有限元模型,考虑材料非线性以及橡胶材料受力过程中的产生的大变形,对图1所示拱形减振橡胶垫进行了有限元计算。
3.1 正常使用状态的应力分析
为了了解应力分布的规律,利用工程软件中的有关路径的定义的功能,在4个不同的平面上定义了15条路径,输出了这些路径上的应力分布情况。图5(黑色圆点表示路径的起始位置)给出了其中的8条路径。计算表明,拱形减振橡胶垫沿着y方向上的应力分布规律大致与沿着x方向的相同,但由于拱形减振橡胶垫的沿x和y方向的尺寸不一样,所以应力分量的数值有所不同。故因篇幅关系,以下只给出y=0平面上的3个路径(路径①,⑤和⑥)和y=7 mm平面上路径③的应力分布图(见图6~9)。

图5 路径示意图Fig.5 The path’s sketch map

图6 路径①的正应力、剪应力分布图Fig.6 The normal stress and shear stress distribution on path①

图7 路径③的正应力、剪应力分布图Fig.7 The normal stress and shear stress distribution on path③
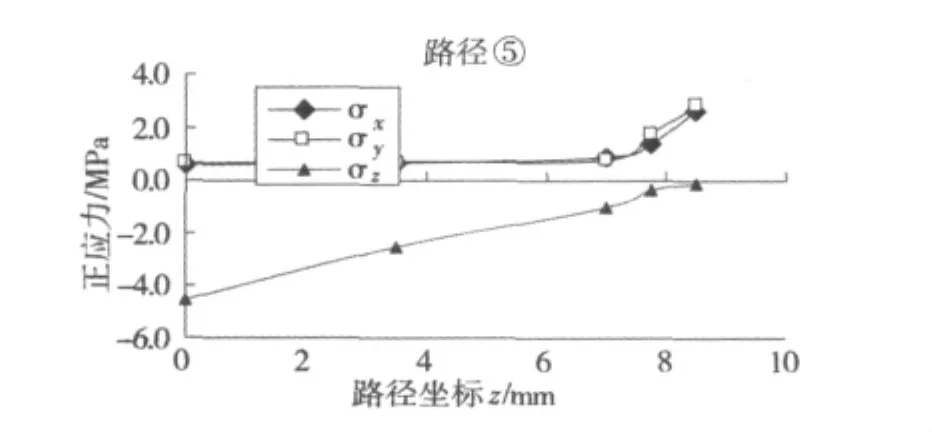
图8 路径⑤的正应力分布图Fig.8 The normal stress distribution on path ⑤
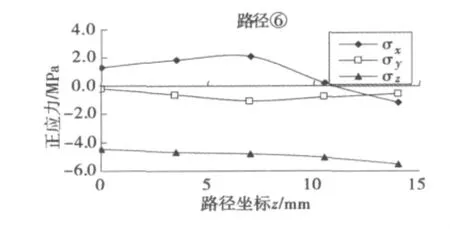
图9 路径⑥的正应力分布图Fig.9 The normal stress distribution on path ⑥
由应力分布图可见,各路径上剪应力数值都较正应力小一个数量级,故下面只分析正应力的分布情况。
(1)路径①是在半球形空腔上方的水平方向路径。在该路径上,应力σx,σy和σz在有半球空腔区域,沿着x方向均呈波浪型的分布,其极大值和极小值出现在半球顶面或2个半球空腔的中心连线的中点附近,σz(沿厚度方向的正应力)为压应力,σx为拉应力,而σy则拉压交替。在无半球空腔区域,σx,σy和σz分布近似呈水平线(σx和σy的值很小),表明应力分布较均匀。由于该条路径正好在半球形空腔的正上方,所以半球空腔的存在对于沿轴重方向的应力σz的影响比较大。
(2)路径③是不在半球形空腔上方的水平方向路径。在该路径上,沿着x方向σx和σy的分布与路径①类似,但极大值和极小值位置与路径①相反。由于该条路径没有在半球形空腔的正上方,所以σz受半球形空腔的影响比路径①较小,即σz的变化幅度很小。
(3)路径⑤是从减振橡胶垫的顶面到半球形空腔顶部的路径。在该路径上σz呈线性分布,在半球形空腔顶达到最小值;σx和σy则大致相同,呈双线性分布,在顶面附近数值很小且几乎为常数,但到半球形空腔顶部时急剧增大,在半球形空腔顶部达到最大值。
(4)路径⑥是两半球形空腔之间的竖向路径,在该路径上σz呈线性分布,在底面处达到最大值,σx和σy在拱形减振橡胶垫的顶部附近和在半球形空腔顶附近呈双线性分布,但数值的变化较小。
(5)路径①和路径③的应力分布大致代表了在整个减振橡胶垫中应力分量沿着水平方向的分布规律。
(6)其他在半球形空腔顶部竖向路径的应力分布同路径⑤的应力分布基本相同,半球形空腔之间的竖向路径应力分布同路径⑥的应力分布基本相同。
(7)边缘附近为无半球区,该处应力状态近似反映实心减振橡胶垫的受力情况。可见,在半球形空腔区的平均应力(静水压应力)明显小于实心区。表明半球形空腔中的压力,有利于减小减振橡胶垫的受力。
3.2 极限承载力分析
减振橡胶垫顶面位移随荷载的变化曲线如图10所示。
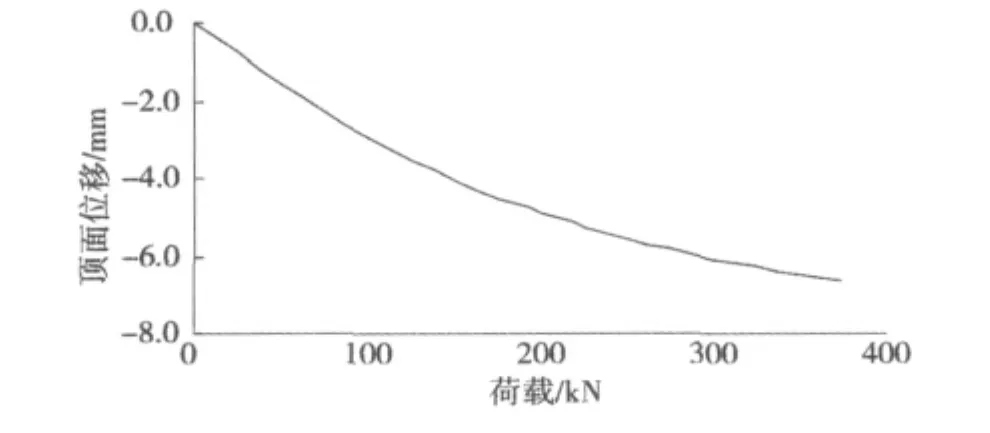
图10 顶面位移-荷载关系曲线Fig.10 The relationship of the surface displacement and load
从计算结果可以看出,拱形橡胶减振垫顶面的位移(压缩量)随着荷载的增加而增加,在荷载均匀增加的情况下,压缩量的增加先快后慢,表现出超弹性材料的性质。该拱形橡胶减振垫垫的极限承载力为375 kN,相对应的顶面位移大小为6.67 mm。这表明,其极限荷载是正常使用下荷载的3倍;当拱形橡胶减振垫的厚度接近其原始厚度的一半时,达到极限状态。
3.3 不同参数时拱形橡胶减振垫的极限承载力
3.3.1 不同R和L时拱形橡胶减振垫的极限承载力
为了考察拱形橡胶减振垫的中半球空腔的半径R、半球间的距离L对拱形橡胶减振垫极限承载力的影响,在不改变拱形橡胶减振垫的外观轮廓尺寸及半球数量的前提下,分别选定了9种不同尺寸的R和L(厚度均为h=14 mm),计算其极限承载力,其主要结果表1所示。
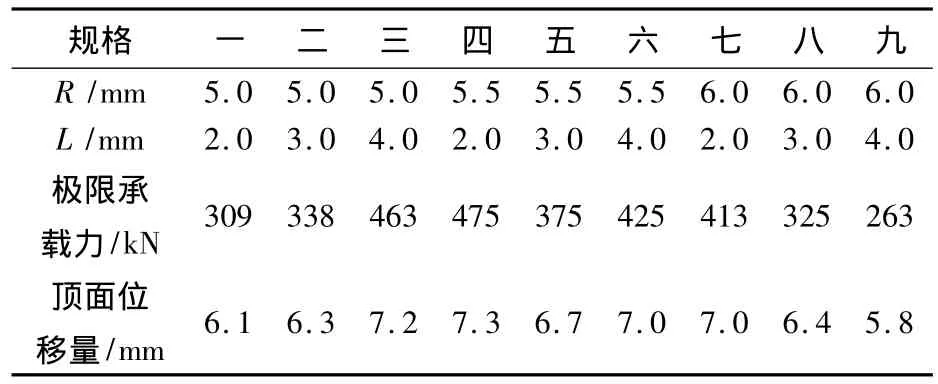
表1 不同R和L的拱形橡胶减振垫的极限承载力和顶面位移Table 1 The ultimate load and top surface displacement of arch decouple rubber bearing in different R and L
从以上结果可以看出:
(1)在半球半径为5 mm时,增加半球之间的间距,极限承载力提高;而在半球半径为6 mm时,极限承载力随半球间距的变化规律则相反。
(2)在半球半径为5.5 mm时,半球之间的距离由2.0 mm增加到3.0 mm时,极限承载力逐渐减小,与在半球半径为6 mm时的变化规律相同;而半球之间的距离由3.0 mm增加到4.0 mm时,极限承载力则逐渐增大,与在半球半径为5.0 mm时的变化规律相同。笔者认为,其原因是:拱形橡胶减振垫可以视为一组弹簧系统,由含空腔部分的弹簧(空气弹簧与空腔上的橡胶弹簧串联)与空腔之间部分的橡胶弹簧并联组成。在半球半径为5.5~6.0 mm时,半球之间的距离由2.0 mm增加到3.0 mm,由于总空腔体积的减少导致含空腔部分的弹簧刚度下降量大于空腔之间部分橡胶由于体积增大导致的弹簧刚度的增大量,故整个拱形橡胶减振垫的总体刚度是减少的。而在半球半径为5.0~5.5 mm时,半球之间的距离由3.0 mm增加到4.0 mm,由于总空腔体积的减少导致含空腔部分的弹簧刚度下降量小于空腔之间部分橡胶由于体积增大导致的弹簧刚度的增大量,故整个拱形橡胶减振垫的总体刚度是增加的。
3.3.2h改变时拱形橡胶减振垫的极限承载力
为了考察拱形橡胶减振垫的厚度对拱形橡胶减振垫的极限承载力的影响,在不改变拱形橡胶减振垫的长宽尺寸及半球数量和半径(取R=5.5 mm)的条件下,分别取3种厚度h=10,14,18 mm,计算其极限承载力,其主要结果见表2。可见,厚度越大,极限承载力越小,相应减振垫顶面位移越大;最大顶面位移约为原始厚度的一半。

表2 不同厚度时的极限承载力和顶面位移Table 2 The ultimate load and top surface displacement in different thickness
4 结论
(1)减振橡胶垫在含半球区域的水平正应力沿着水平方向基本上呈波浪型的变化,沿竖向基本上呈线性分布;剪应力比正应力小一个数量级。
(2)无半球区域应力分布比较均匀,变化很小。
(3)拱形减振橡胶垫中的半球形空腔的半径R、半球间间距L和厚度h对极限承载力均有一定的影响。
(4)当R=5.5 mm,L=3 mm,h=14 mm 时,拱形橡胶减振垫的极限承载力为375 kN,与正常使用下的荷载之比为3∶1。
(5)极限承载力状态时,最大顶面位移约为原始厚度的一半。
[1]史守峡.平面应力不可压缩橡胶薄片的非线性有限元分析[J].哈尔滨工程大学学报,1998,19(3):11 -15.
SHI Shou-xia.A finite element analysis of large strains of nearly incompressible rubber sheet[J].Journal of Harbin Engineering University,1998,19(3):11 -15.
[2]特雷劳尔 L G R.橡胶弹性物理学[M].北京:化学工业出版社,1982.
Terleilaoer L G R.The elastic physics of rubber[M].Beijing:Chemistry Industry Publishing Company,1982.
[3]弗雷克利P K,佩恩A R.橡胶在工程中应用的理论与实践[M].北京:化学工业出版社,1985.
Fuleikli P K,Pein A R.The theory and practices of the application of rubber in engineering[M].Beijing:Chemistry Industry Publishing Company,1985.
[4]朱 敏.橡胶化学与物理[M].北京:化学工业出版社,1984.
ZHU Min.Chemistry and physics of rubber[M].Beijing:Chemistry Industry Publishing Company,1984.
[5]王 伟,邓 涛,赵树高.橡胶Mooney-Rivlin模型中材料常数的确定[J].特种橡胶制品,2004,25(4):8-10.
WANG Wei,DENG Tao,ZHAO Shu-gao.Determination for material constants of rubber mooney-rivlin model[J].Special Purpose Rubber Products,2004,25(4):8 -10.
[6]易太连,翁雪涛,朱石坚.不可压缩橡胶体的静态性能分析[J].海军工程大学学报,2002,1(14):76 -80.
YI Tai-lian,WENG Xue-tao,ZHU Shi-jian.Analysis of static characteristics of nearly incompressible rubber materials[J].Journal of Naval Engineering University,2002,1(14):76-80.
[7]朱伯芳.有限单元法原理及应用[M].2版.北京:中国水利水电出版社,1998.
ZHU Bo-fang.The theory and application of finite element method[M].Second Edition.Beijing:China Water and Electricity Press,1998.
The stress analysis of the arch rubber bearing in the action of load
CHEN Yu-ji1,LUO Qi-zhi1,2
(1.Department of Civil Engineering and Architecture,Foshan Science and Technology University,Foshan 528000,China;2.School of Civil Engineering,Hunan University,Changsha 410082,China)
Mooney-Rivlin constants of rubber materials were determined by the test.The space finite element model of the arch decouple rubber bearing was established.Taking material nonlinearity and geometry nonlinearity as well as the action of the air pressure in semisphere empty rooms into account,the stress distribution and ultimate load of the arch decouple rubber bearing with semisphere empty rooms were analyzed with the finite element method.It is shown from the calculation result that in the common use state,the normal stresses in the area with semisphere empty rooms change mainly at wavy rule along horizontal direction and linearly along vertical direction;the shear stress is an order of magnitude lower than the normal stress;the distribution of stresses in the area without semisphere empty rooms are much average and the stresses change very little.The semisphere radiusR,spaceLbetween semispheres and thicknesshof the arch decouple rubber bearing have some influence on the ultimate load.WhenR=5.5 mm,L=3 mm,h=14 mm,the ultimate load of each arch rubber bearing is 375 kN,which is three time of the load in the common use state.The thickness of the arch decouple rubber bearing in ultimate state is approximately half of the original thickness.
the decouple rubber bearing;super elastic materials;stress;top surface displacement;ultimate load
O344
A
1672-7029(2011)06-0023-06
2011-05-12
国家自然科学基金资助项目(50978058);广东省自然科学基金资助项目(S2011010005037)
陈玉骥(1962-),男,海南文昌人,教授,博士,从事土木工程结构分析和弹塑性力学及其应用研究
