铁路突发事件应急物资优化调配＊

张彦春，范艳萍，杨小礼

(1.中南大学土木工程学院，湖南 长沙 410075;2.广州铁路集团公司 株洲工务段，湖南 株洲 412000)

铁路突发事件应急物资优化调配＊

张彦春1，范艳萍2，杨小礼1

(1.中南大学土木工程学院，湖南 长沙 410075;2.广州铁路集团公司 株洲工务段，湖南 株洲 412000)

为求解满足应急开始时间最早及经济性最优的铁路应急物资优化调配问题，通过分析铁路应急物资调配的特点，运用多目标规划方法建立铁路应急物资调配模型，设计了求解步骤及算法，并进行了算例验证。研究结果表明:该模型能够实现应急开始时间最早、出救点最少及应急运输费用最少等目标，进而实现铁路应急物资的高效利用与合理调度。

铁路突发事件;应急物资;调配;优化

铁路作为国民经济的大动脉，经常发生各类突发事件。应急物资是铁路突发事件应急处置与救援的关键要素之一。应急救援的最显著特点表现为时间的紧迫性，决策者必须以最短的时间完成应急调配方案，其时间效益高于经济效益。然而，应急物资调配不应该是不惜一切代价、一哄而上，必须在满足应急开始时间最早的前提下兼顾应急调配的经济性。

对于大规模突发公共事件的应急物资调配问题，许多学者进行了研究。从调配目标来看，分为单目标和多目标调配问题。单目标为应急时间(从事件发生到物资到达应急地点的时间)最早或者限制期条件下最小延迟时间。多目标除考虑应急时间外，还将应急资源调配成本最小作为优化目标，一般以出救点数目最少或动员系统成本最小来体现。如何建敏等［1］针对单资源一次消耗系统和连续消耗系统以及多资源问题，建立了最小化应急开始时间的单目标模型;刘春林等［2－3］对单资源一次消耗系统利用模糊规划方法建立多目标模型求解，并讨论了物资需求约束条件下多个出救点的紧急物资调度问题。姜金贵等［4］综合考虑物资调运成本和物资缺失损失费用，建立了单资源调运总成本最小化的数学模型，并利用粒子群算法进行求解［4］;刘北林等［5－6］分别就单资源、一次消耗系统和多资源调配问题建立多目标模型，并利用理想点法求解。对于铁路应急物资调配问题，目前的研究成果较少［7－8］。铁路应急物资的调配与突发公共事件应急物资的调配有所不同，需要在分析铁路运营及铁路应急物资调配特点的基础上建模求解。

1 问题分析

作为应急救援最根本的要素之一，应急物资必须在尽可能短的时间内运抵现场参与救援。因此，铁路应急物资调配问题首先应考虑时间效应最大化，以应急开始时间最早作为应急物资调配的首要目标。其次，动用的储备点(称为出救点，下同)越少，可以在一定程度上减少人员费、装卸费等杂费，也可以减少事后补充库存的相关费用，故出救点数目最少也是优化的目标。另外，铁路应急物资的运输涉及铁路和公路运输，2种运输方式的运费不同。一般来讲，铁路单位货物运输费用低于公路运输费用。因此，应通过合理选择运输方式使应急物资运输费用最低。

本文通过建立多目标数学模型，求解在满足应急开始时间最早的前提下，合理运用公路和铁路运输方式进行应急物资调配，使出救点数目最少、运输费用最小。

模型假设如下:

(1)物资为一次性消耗系统，即当所有的物资到达应急地点后才能开始应急活动的应急系统;

(2)一条铁路线路上仅有一个地点发生突发事件，即除事发地点外的铁路线路是畅通的;

(3)同一出救点的物资仅采用一种运输方式;

(4)全铁路局应急物资储备量是充足的。

2 模型建立

采用铁路运输时，各可出救点Ai到应急地点A的铁路里程为di'，运输时间为ti'，单位应急物资的运输费(包括装卸费等其他运输费用，下同)为c';采用公路运输时，各出救点Ai到应急地点A的公路里程为d″i，运输时间为ti″，单位应急物资的运输费为c″，令ti=min{ti'，。

用T(φ)表示方案φ对应的应急开始时间，显然有:

用χ表示所有方案构成的集合。设二元变量和，当某一储备点物资运输采用铁路运输时，令1，根据模型假设，此时=0;相反，若采用公路运输，则0，1。

出救点数目以N(φ)表示，运输费用以C(φ)表示，则:

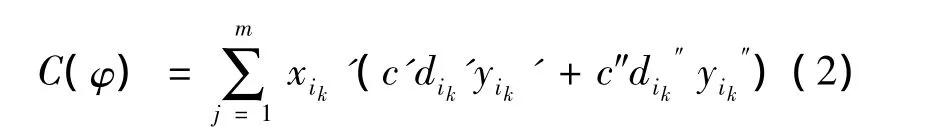
多目标函数如下:

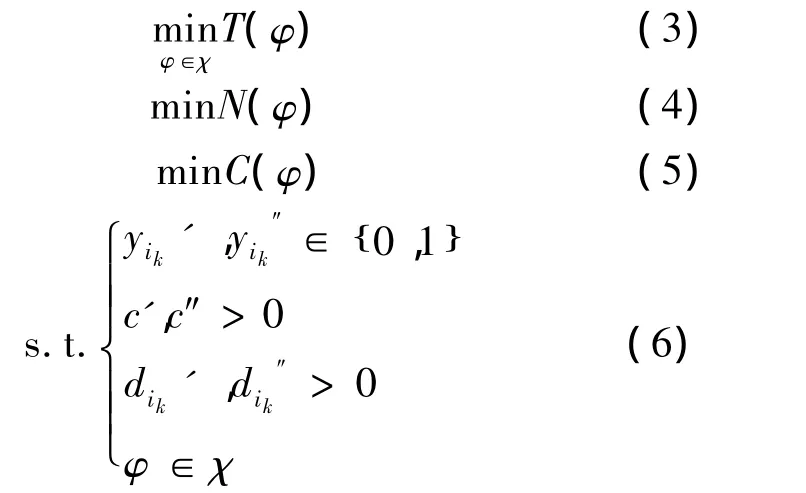
式(3)使应急开始时间最早;式(4)使出救点数量最少;式(5)使应急运输费用最少;式(6)为约束条件。

3 模型求解步骤及算法

根据问题分析，在以上多目标函数问题中，必须将应急开始时间最早作为优先满足的目标，先求解满足时间最短的初步方案，在此基础上，再求解满足其他2个目标的最优方案。

3.1 求解满足时间最短的初步方案

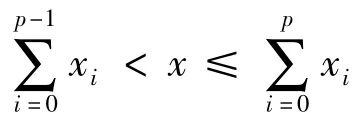
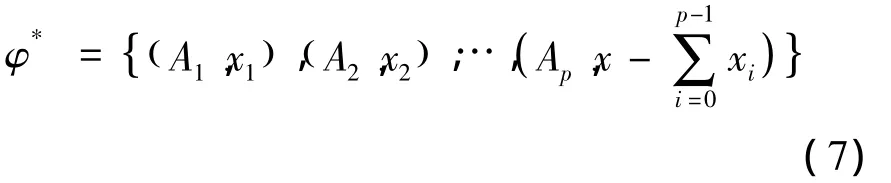
该方案即为:选取利用铁路或公路运输能最快到达应急地点A的储备点A1参与应急，如果它的全部物资x1小于需求量x，再调用第二到达的出救点A2的物资参与应急，如果x1和x2的全部物资量之和x1+x2仍小于需求量x，则调用第三到达的出救点A3的物资参与应急，依此类推，直至满足应急物资的需求。因为t1≤t2，…，≤tn，方案φ*中，在tp之前能够到达的全部物资量肯定小于x，故φ*是(φ)的最优解(但不是多目标函数的最优解)，(φ)=tp。

3.2 求解满足出救点最少的方案

方案φ*给出了满足应急开始时间最早的方案组合，但从出救点数量和考虑铁路公路2种运输方式下的最小费用来看，并不是最优方案。应在方案φ*的基础上求解满足出救点最少的方案。

使得式(4)达到最优，且N(φ)=r。

3.3 求解满足运输费用最少的最优方案

满足出救点数N(φ)=r的方案φ＊＊所对应的方案组合可能不唯一(见算例)，由于方案φ＊＊优先选择储备量大的储备点参与救援，从运输费用上来讲，φ＊＊不一定是最优方案。因此，可以在满足N(φ)=r的若干方案中选择运输费用最低的调配方案，也就确定了各储备点采用的运输方式。

将满足N(φ)=r的各方案的相应数据代入式(2)，可得各方案的运输费用，选择运输费用最低的方案即为式(5)的最优方案，也是满足应急开始时间最早、出救点最少、运输费用最低的调配方案。

3.4 算 法

由以上步骤，设计以下算法。

(1)j=n，v=0。

(2)将各储备点按物资量x1，x2，…，xj由大到小排列，得，…，求出该序列对x的临界下标u。若存在u，v=v+1，组合方案 φv=，求出T(φv)，N(φv)，转(3);若不存在u，转(5)。

(3)j=j－1。

(4)若tj=tj+1，转(3);否则转(2)。

(5)若

则满足T(φv)最小基础上N(φv)最小的方案为多个，分别设为 φu，φu+1，…，φj－u，将各方案相应数据代入式(2)，求出各方案对应的C(φu)，C(φu+1)，…，C(φj－u)， 取 min(C(φu)，C(φu+1)，…，C(φj－u))所对应的方案即为上述多目标规划模型的最优解。

4 算例

某铁路突发事件发生后，应急点需要某种应急物资量为50单位。要求从9个储备点中选择出救点及运输方式，使应急开始时间最早，出救点最少，且调配费用最少。表1给出了各储备点到达应急点的铁路、公路运输时间、各储备点的物资储备量、铁路、公路单位运输费用以及运输距离。

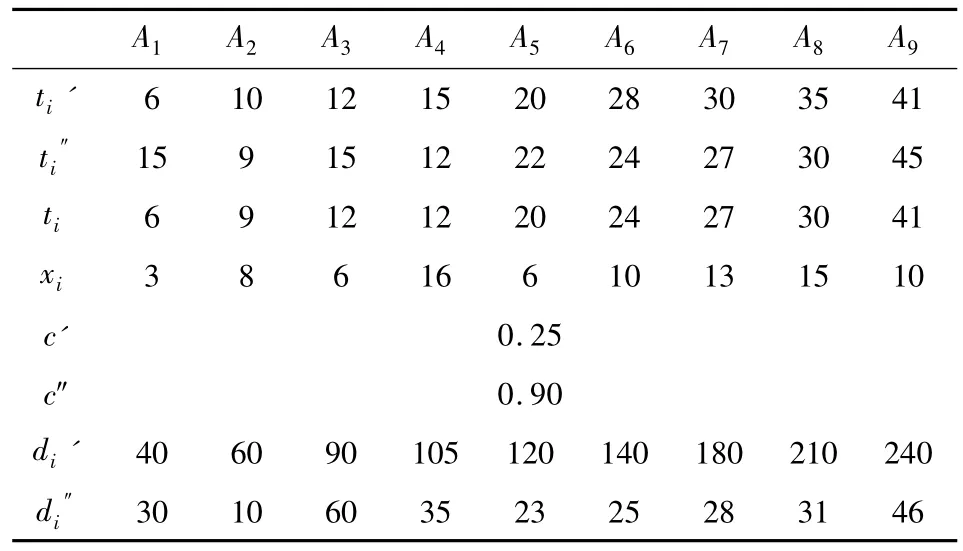
表1 某应急物资调配相关数据Table 1 Related data on a case of railway emergency materials dispatching

采用前文算法，运算过程及结果见表2。

表2 方案选择运算过程Table 2 Operational process of scheme selection

记 {(A4，16)，(A7，13)，(A6，10)，(A2，8)，(A3，6)}为方案，将j=7的方案组合{(A4，16)，(A7，13)，(A6，10)，(A2，8)，(A3，6)，(A5，6)，(A1，3)}代入式(9)，可知方案={(A4，16)，(A7，13)，(A6，10)，(A2，8)，(A5，6)}和方案={(A4，16)，(A7，13)，(A6，10)，(A2，8)，(A1，3)}也满足min(N(φv))=5的要求。这3个方案组合中，A6和A72个储备点由于运输时间的限制，必须采用公路运输。其他储备点物资的运输方式可通过分别比较2种运输方式运费的大小进行选择，A1，A2，A3，A4和A5等5 个储备点的铁路、公路运输费用计算结果见表3。

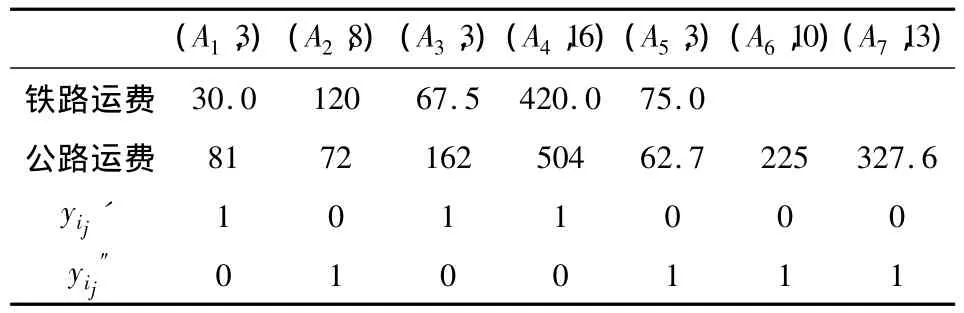
表3 运输费用计算表Table 3 Transport cost of different mode

最后，分别将相关数据代入式(2)，求得:C()=1112.1，C()=1107.3，C()=1074.6。所以，方案={(A4，16)，(A7，13)，(A6，10)，(A2，8)，(A1，3)}为最优方案，相应的运输方式分别为铁路、公路、公路、公路、铁路。

5 结语

运用此多目标规划模型及算法可以实现铁路应急救援开始时间最早、出救点最少及应急调运费用最低等目标。以此为基础建立铁路应急物资调配智能决策系统可以实现应急物资的快速、高效调配。

［1］何建敏，刘春林，曹 杰.应急管理系统——选址、调度与算法［M］.北京:科学出版社，2005.

HE Jian-min，LIU Chun-lin，CAO Jie.Emergency management and emergency system －location，dispatching and algorithm［M］.Beijing:Science Press，2005.

［2］刘春林，何建敏，盛昭瀚.应急系统调度问题的模糊规划方法［J］.系统工程学报，1999，14(4):351－355.

LIU Chun-lin，HE Jian-min，SHENG Zhao-han.Fuzzy programming in selection of multi－depot for emergency systems［J］.Journal of Systems Engineering，1999，14(4):351－355.

［3］刘春林，何建敏，盛昭瀚.多出救点应急系统最优方案的选取［J］.管理工程学报，2000(1):13－15.

LIU Chun-lin，HE Jian-min，SHENG Zhao-han.Selection of multi－depot in emergency system［J］.Journal of Industrial Engineeringand EngineeringManagement，2000(1):13－15.

［4］姜金贵，梁静国.基于粒子群优化算法的应急资源调度研究［J］.统计与决策，2009(2):53－54.

JIANG Jin-gui，LIANG Jing-guo.Emergency resources scheduling based on particle swarm algorithm［J］.Statistics and Decision，2009(2):53－54.

［5］刘北林，马 婷.应急救灾物资紧急调度问题研究［J］.哈尔滨商业大学学报:社会科学版，2007(3):3－5.

LIU Bei-lin，MA Ting.Research on the scheduling problem of emergency materials［J］.Journal of Harbin University of Commerce:Social Science Edition，2007(3):3－5.

［6］汪 欲，何建敏.应急系统中多资源出救方案的研究［J］.东南大学学报:自然科学版，2002，32(3):510－513.

WANG Yu，HE Jian-min.Research on multi－ resource dispatch in emergency system ［J］.Journal of Southeast University:Natural Science Edition，2002，32(3):510 －513.

［7］王玲玲.多出救点应急调度研究［J］.铁道运输与经济，2010，32(7):47 －52.

WANG Ling-ling.Study on multi－ depot emergency scheduling ［J］.Railway Transportation and Economy，2010，32(7):47 －52.

［8］王 军.铁路重大突发事件应急资源优化调配问题的研究［D］.北京:北京交通大学，2007.

WANG Jun.Research on emergency resource dispatch optimization in railway major emergency［D］.Beijing:Beijing Jiaotong University，2007.

Optimization on railway emergency materials dispatching

ZHANG Yan-chun1，FAN Yan-ping2，YANG Xiao-li1

(1.School of Civil Engineering，Central South University，Changsha 410075，China;2.Zhuzhou Track Maintenance Division，Guangzhou Railway(Group)Corporation，Zhuzhou 412000，China)

In order to solve the problem of railway emergency materials dispatching optimization with the objects of the earliest rescuing start time and economic optimization，this paper established the railway emergency materials dispatching model by ways of analyzing the characteristics of railway emergency materials dispatching and utilizing multi－objective programming method.It also designed solving steps and algorithm and then carried out example testing for this model.The research result indicates that the model can achieve the objectives namely the earliest rescuing start time，the minimum number of selected depots and minimum cost of dispatching and the model can ensure utilizing and dispatching the emergency materials efficiently and methodically.

railway incidents;emergency materials;dispatch;optimization

F532.6

A

1672－7029(2011)06－0103－04

2011－11－10

铁道部科技研究开发计划项目(2010X011－A)

张彦春(1974－)，女，黑龙江哈尔滨人，讲师，博士，从事项目管理与应急管理研究