连续型物流设施选址的区间决策模型及算法*
2011-06-02李利华胡正东
李利华,符 卓,胡正东,3
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.长沙理工大学交通运输工程学院,湖南长沙 410004;3.南华大学 政治与公共管理学院,湖南 衡阳 421001)
连续型物流设施选址的区间决策模型及算法*
李利华1,2,符 卓1,胡正东1,3
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.长沙理工大学交通运输工程学院,湖南长沙 410004;3.南华大学 政治与公共管理学院,湖南 衡阳 421001)
考虑物流需求的不确定性,以区间数度量不确定性参数及变量,构建多商品、多节点的连续型物流设施选址区间决策模型,通过区间可能度判别区间解的性质与大小,设计问题求解的区间迭代遗传算法。算例测试结果表明,求解结果具有较强的实践可操作性,可以作为物流节点选址决策的参考方法。
物流设施选址;区间决策;不确定性;重心法;遗传算法
随着经济一体化的快速发展,社会物资需求不断加大,商品交换速度加快,推动现代物流业的迅速发展。日益扩大的社会物流需求使得专业化运作的物流(配送)中心、物流园区等现代化的物流运作模式发展迅速,今后相当长的一段时期内还将面临物流网络资源的优化与整合问题。物流设施选址问题是现代物流科学、合理、持续发展的关键,一直以来都得到学术界与实际应用的广泛重视。物流设施选址是一个系统决策问题,其决策方法分为离散型设施选址(DFLM)与连续型设施选址(CFLM)2类。其中连续型方法主要解决的是在一个连续的平面区域中对物流节点的选择与决策。针对该问题,目前在方法改进与实践应用中取得大量成果,如鲁晓春等[1]构建流通费用偏微分方程的重心法,并进行实证分析;姜大立等[2]以运费与损失费的微分方程构建易腐物品配送中心连续型选择模型,设计遗传算法的求解思路,并进行实际案例验算;邹辉霞等[3]讨论了单配送中心离散选择问题;邱法聚等[4]构建由工厂、配送中心、用户等组成的3层物流配送网络的连续型选择模型,并对加油站的石油配送案例进行分析;杨茂盛等[5]考虑了决策节点费用,改进重心法模型;辜勇等[6]应用重心法对江岸区石油油库选址问题进行实证分析。
研究表明,连续型物流设施的选址决策方法的理论基础为重心法,该方法能够成功应用于物流行业且能作为实践决策的依据。然而,随着物流行业的快速发展及变化,受费用约束、需求变动、发展环境等诸多因素的影响,不确定性的物流设施选址决策问题日益突出。近年来,不确定性物流规划[7-10]问题的研究广受关注。物流节点选址一旦决策并形成实践,就是一个长期的过程,很难改变,而一些不确定性因素就是导致决策失误的根源,现实中这样的案例比比皆是,很多已经决策建成的物流节点处于不能运营的状态。针对不确定性的物流节点选址决策已有大量的研究成果[7-10],目前的研究方法主要集中于应用随机决策与模糊决策解决不确定性问题。区间决策[11]是解决不确定性决策的一种重要手段,由Moore等[12]于1959年提出,其基本理念是运用区间数和区间算法解决不确定性问题,Csallner等[13-15]分别对带区间数的优化规划问题进行探讨。运用区间决策对不确定性的物流设施选址问题的研究并不多见。
本文提出连续型物流设施选址的区间决策模型,对不确定性物流规划问题进行研究。
1 区间决策模型的构建
1.1 区间物流决策的基本度量
区间物流决策是以区间数的形式来度量不确定性变量,运用区间运算法则,实现物流设施选址模型的确定性转化,结合区间优化算法求解。区间数的表达形式为:
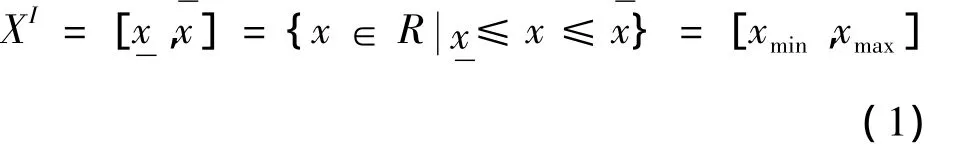
式中:XI为区间变量x所在区间;为区间下界;,xmax为区间上界;x为区间变量。
如在物流需求网络中费率函数C通常被认为是一个不固定的变量,可以用区间的形式来标度该变量取值的上界和下界。区间决策模型以区间变量进行运算,满足实数运输的交换律、结合律等。
1.2 模型的构建
连续型物流设施选址的基本模型为重心法,该方法的基本思想为:在一个连续的平面区域内,定义坐标体系结构,区域中存在多个需求用户点,各用户点对应的平面坐标已知,而要决策选址的物流节点可以在该平面区域任何一点存在,其平面坐标未知。同时已知待决策物流节点至各用户点的物流运输费率与配量,因此,可以定义节点间的配量为已知节点的重量,问题转化为求一个物体的平面几何重心。
对物流网络基本结构标定如下:网络一共有m(1≤i≤m)个用户点,从待决策物流节点共有q(1≤k≤q)种商品需要配送至用户点,各用户点的坐标为(Xi,Yi)(1≤i≤m),决策节点坐标为(xj,yj)(1 ≤j≤n,n为物流节点决策的数目),决策节点至用户点的运费与配量分别表达为Ckij(第j个决策节点第k种商品至第i用户点的费率函数),Qkij(第j个决策节点第k种商品至第i用户点的配量);定义一个决策点选择平面范围的矩形区域D(通常为计算的方便性,以坐标系的第一象限标定,故各节点的坐标均为正值),起点为(a0,b0),终点为(a1,b1)。按照需要所求决策节点的数目,将整体平面分为n个小的片区Dj(1≤j≤n),表示一共要选择n个物流节点,一个片区对应一个待选择物流节点,并且各片区规定其各自的坐标区域范围。
由于物流网络结构存在不确定性,故区间标度下的决策模型为:


为第j个决策节点第k种商品至第i用户点的区间运输费率;为第j个决策节点至第i用户点运距的区间非直线系数;为第j个决策节点至第i用户点的欧式距离;QIkij为第j个决策节点第k种商品至第i用户点的区间物流配量;Wkij为0-1变量,若Wkij=1表示用户i的第k种商品需求由物流节点j负责;若Wkij=0则否之。
模型中:目标函数(2)以系统的总体费用最小为目标,衡量的决策节点至用户点运输过程中实际运行线路不能等同于两点间的直线距离,作为修正系数;表示决策点至用户点的直线距离。约束条件(3)表示决策节点在允许选址区间范围内的坐标约束。
2 模型的求解与算法实现
2.1 模型的求解思路
上述模型中,以及为不确定性变量,由于该3个变量的不确定性而引发最终求解结果的不确定性,故最终的决策点坐标应该是,)的形式。而由式(2)与(3)所确定的模型结构是一个仅目标函数含有区间不确定性变量的连续型的非线性规划问题,约束条件不受不确定性变量的影响,问题的求解仅需对目标函数确定转化后进行。
由于平面区域D定义在第1象限,故所有的区间变量与区间参数都为非负约束,所求最终决策结果也在第1象限。由区间运算法则,以及满足区间乘法运算规则,可以直接进行问题的确定性转化,但由于的区间运算涉及到交换律,表现为弱的形式,故存在一定的不确定性,其标定形式为:

在式(4)与(5)中,存在二选一的行为,由于该问题求解的基本思想为迭代法,在已知上一轮解集的基础上,求下一轮解集,故很容易通过比较得出与的取值。因此上述模型可以确定性转化为:
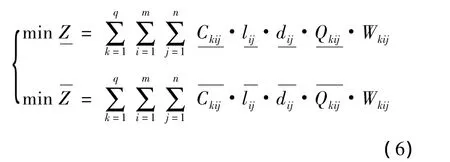
对于该类连续型决策命题,决策变量xj和yj可以在允许的区间范围中随意取值,故其满足最小二乘法的运算要求,对目标函数分别求xj和yj的偏导数可得到:
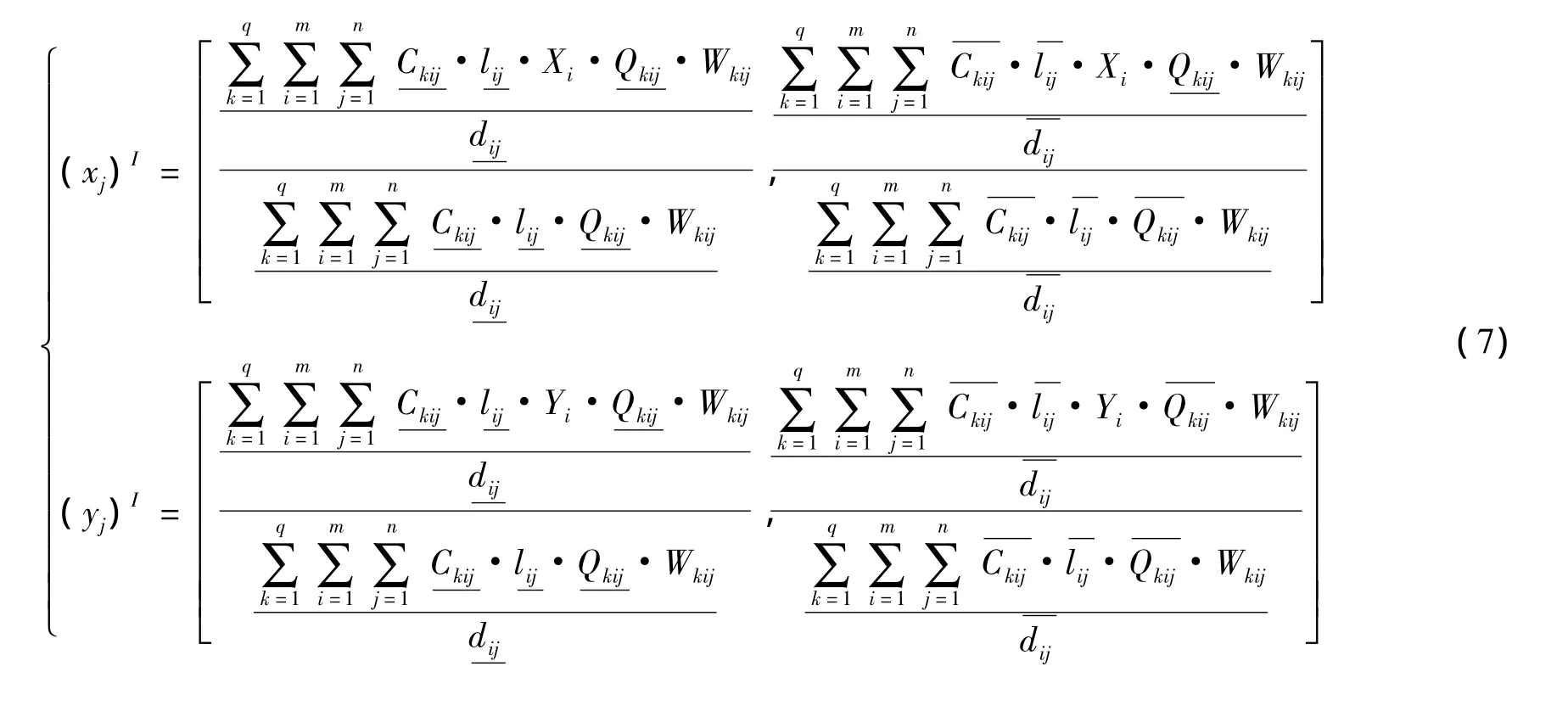
2.2 算法设计
式(7)为在不同的区间参数下,待决策物流节点的最终区间坐标值。由于决策变量xj和yj的计算公式中包含未知变量,故可运用区间迭代法对该问题求解,考虑到计算的复杂性以及反复迭代的要求,本文提出区间模式下的遗传算法对该问题求解,其步骤如下:
(1)初始区域的标定
定义求解的区域范围,以坐标区域的形式标定D。由于需要决策的物流节点为n个,将决策的平面连续区域D分为n个小的区域,每个区域定义为Dj(1≤j≤n),表示在每个小的区域存在一个待决策物流节点,且对各Dj进行坐标范围的标定;
(2)遗传变量编码
以计算机随机选择,定义染色体或个体,即在各Dj中分别定义待决策节点的初始坐标编码:

(3)初始种群的定义
在各区域Dj中随机产生一系列的节点(,),r代表选择的数目,构成r个染色体或个体gr,组成初始种群集G=(g1,g2,…,gr),在g0情况下,进化代数gen=0,设定进化最终代数N;
(4)构建适应度函数
适应度函数是对解集环境适应性的一种评价,物流节点决策问题的目标就是要使得系统总成本最小,满足适应度函数的设置条件,故以(xj,yj)为确定区间状态下的系统成本最优为适应度函数进行标定;
(5)计算初始区间解
将初始解代入到目标函数式(6)中,计算minZI初始值,得min(ZI)0;
(6)第一轮迭代
将初始解代入到式(7)中,计算得出迭代后各节点区间决策结果:
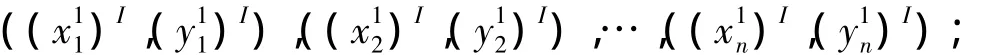
(7)计算结果区域检验
检查各决策节点的坐标区间是否属于对应的Dj,若(()I,()I)∈Dj,则继续;若决策节点的区间取值超出Dj范围,则将()I,()I)的区间坐标上下界改为Dj的区间上下界,继续;
(8)新的迭代结果
将上述计算结果代入式(6),得到新的min(ZI)1;
(9)区间解的性质判别
判别两个比较区间解的相互关系,若min(ZI)0与min(ZI)1关系为区间不相交或区间包含,直接标定解的最优;若二者关系为区间相交,则按如下公式:
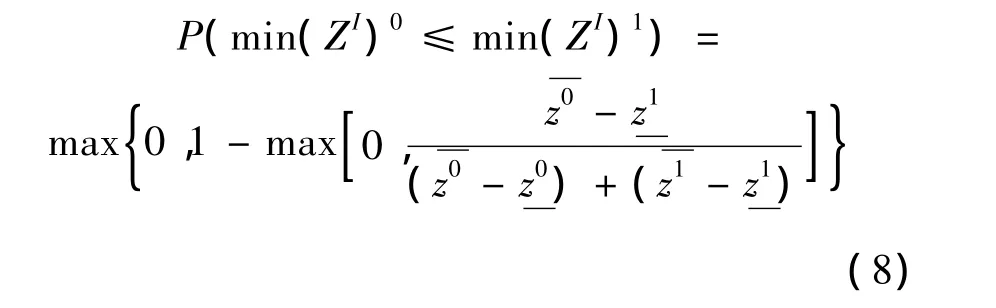
计算区间可能度,若P≥0.5则min(ZI)1>min(ZI)0,反之min(ZI)1<min(ZI)0;
(10)区间解的结果比较
若min(ZI)1>min(ZI)0,则表明原始解:
(,),),…,,)为最终解;反之,则返步骤(5),进行下一轮迭代,直至t次迭代后,min(ZI)t+1>min(ZI)t,则 min(ZI)*=min(ZI)t为最终解,对应决策节点为g*=((,),(),…,(,))为最终决策区间解。
(11)遗传复制
根据染色体适应度的大小重新排序,设定其复制到下一代的概率ps,用轮盘式算子对个体进行复制,进入下一代,gen=1;
(12)交叉重组
在交叉概率ps下,在概率区间[0,1]中重复产生随机数t,直到与种群个数数量相等为止,选择小于ps的随机数对应的个体,对新的个体两两交叉配对,如果选择的个体为奇数,则去掉一个个体,在[0,1]区间中的随机产生数e,对于每一个交叉配对,按以下方式进行交叉操作:

其中:g1,g2为当前2 个个体,而 (g1)',(g2)'为交叉操作后产生的2个新的个体。
(13)遗传变异
设定遗传变异概率pw,在随机数t中,选择小于pw的随机数对应的个体,随机产生一个方向λ,对染色体进行如下变异:

其中:(g2)'为变异后的新个体,M为一正数。
(14)自然选择
对新的个体在适应度函数下进行重新排序,排在最后的染色体性能最差,将其用上一代最优染色体代替。
(15)结果输出
以gen=gen+1依次进化操作,当gen=N时,停止计算操作,确定当前群体中的第一个染色体g中对应的求解结果为最终解。
3 算例分析
某物流企业拟在一城市范围内构建其产品的配送体系,其生产商品种类数q=4,网络用户节点m=10个且其地点已知,拟在区域范围内选址n=2个配送中心,网络的区间参数见表1和表2。

表1 第1个决策节点至用户点的区间标量Table 1 Interval scalar from the first decision node to the user demand nodes

表2 第2个决策节点至用户点的区间标量Table 2 Interval scalar from the second decision node to the user demand nodes
构建区域坐标体系,令区域范围为(0,0)到(80,80),则相对应的10个用户点的坐标可以标定为(3.5,12.7),(20.2,7.8),(45.3,18.9),(63.2,24.9),(71.5,59.8),(16.5,73.2),(54.7,47.8),(33.5,69.8),(17.9,45.6),(32.1,23.9)。划定两个片区D1和D2,其对应的区域范围为D1(0,0)到 (40,40),D2(40,40)到(80,80),同时考虑决策区域D内的运输网路布局、地形地貌特征等因素,通过调查分析可知,D1范围的非直线系数[1.0,1.4],D2范围的非直线系数[1.1,1.4],遗传进化代数N=300。则通过计算得出区间决策选址结果如下:
如图1所示的遗传进化求解过程可知,初始解情况下,目标函数的区间值在800 000~1 000 000之间,是一个非常庞大的数据,而通过遗传进化迭代求解后,在进化至50代左右,目标函数的求解结果基本区域稳定,按照设置的进化代数N=300,得 到 最 终 的 min(ZI)=[156732.54,177 821.36],决策的2个物流节点区间坐标为:(,)=([16.7,18.5],[35.4,37.1]),(,)=([46.2,48.3],[54.6,57.8])。

图1 案例求解过程图Fig.1 Process diagram of example solution
由此可知,通过区间运算,得出的目标函数为一区间值,决策节点坐标可以在相应的区域内选择,图2中,第1个配送中心横坐标的选择空间为[16.7,18.5],纵坐标为[35.4,37.1],即表示受不确定性因素约束,在该区间范围内对第1个配送中心决策选址,能够保证目标函数具有最小区间值,第2个配送节点亦然。
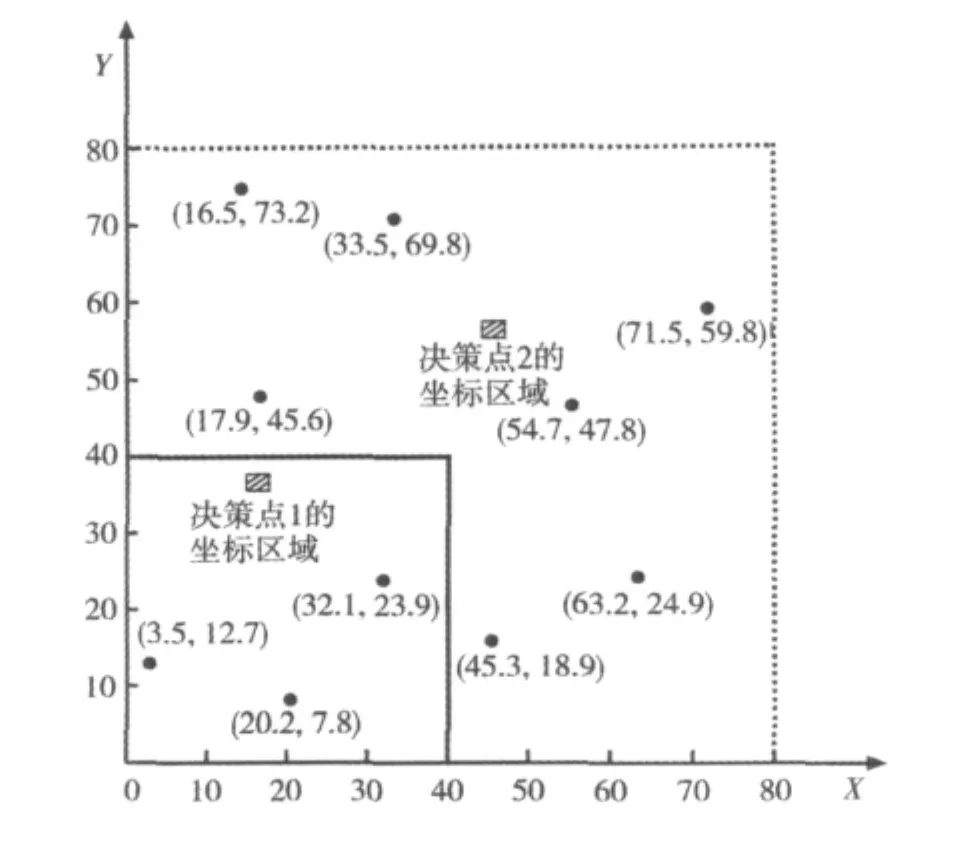
图2 案例求解坐标结构图Fig.2 Structure diagram about coordination of example solution
4 结语
提出运用区间决策对连续型物流节点选址问题的求解方法,能够解决2个问题:(1)考虑不确定性因素对决策问题带来的影响。如模型中的节点间的运输费率、配量需求等,在实际决策问题中,其本身就是不断变化,不是固定值,因此,文中以区间值标度符合实际情况;(2)避免精确坐标选址的弊端。传统方法计算结果为决策节点的精确坐标,而在实际中,计算的坐标点往往是不可用于节点的建设,本文方法计算的结果为区间值,表明可以在一个“有限的区域”范围内进行选址点的决策,实际可操作性更强。
[1]鲁晓春,詹荷生.关于配送中心重心法选址的研究[J].北方交通大学学报,2002,24(6):108 -110.
LU Xiao-chun,ZHAN He-sheng.Study on address selection of distributing center using barycentric method[J].Journal of Northern Jiaotong University,2002,24(6):108-110.
[2]姜大立,杨西龙.易腐物品配送中心连续选址模型及其遗传算法[J].系统工程理论与实践,2003(2):62-67.
JIANG Da-li,YANG Xi-long.Genetic algorithm for continuous location problem of physical distribution center for decaying product[J].System Engineering Theory and Practice,2003(2):62-67.
[3]邹辉霞,高 伟.单配送中心的离散选址模型[J].科技进步与对策,2004(1):77-78.
ZOU Hui-xia,GAO Wei.A discrete location model single distribution center[J].Science and Technology Progress and Policy,2004(1):77-78.
[4]邱法聚,张予川,易 荃.物流配送中心连续型选址模型的推广[J].物流科技,2007(1):16-19.
QIU Fa-ju,ZHANG Yu-chuan,YI Quan.Extension of continuous model for logistics distribution center location[J].Logistics Sci-Tech,2007(1):16-19.
[5]杨茂盛,李 霞.改进重心法在物流配送中心选址中的应用[J].物流技术,2007(6):60-62.
YANG Mao-sheng,LI Xia.Application of improved gravity method in location of logistics distribution center[J].Logistics Technology,2007(6):60-62.
[6]辜 勇,高东旭.重心法在油库选址问题中的应用[J].物流技术,2007(2):108 -111.
GU Yong,GAO Dong-xu.Research on optimization of location selection of finishec oil distribution center[J].Logistics Technology,2007(2):108-111.
[7]刘宝碇,赵瑞清,王 纲.不确定规划及应用[M].北京:清华大学出版社,2003.
LIU Bao-ding,ZHAO Rui-qing,WANG Gang.Uncertain programming with applications[M].Beinjing:Press of Tsinghua University,2003.
[8]戎晓霞,崔玉泉,马建华.不确定环境下的物流配送中心选址模型[J].山东大学学报,2004,39(6):72 -77.
RONG Xiao-xia,CUI Yu-quan,MA Jian-hua.Allocation models for logistics system in uncertain environments[J].Journal of Shandong University,2004,39(6):72 -77.
[9]刘 琼,叶晶晶,邵新宇.不确定信息条件下制造/再制造物流网络优化设计[J].华中科技大学学报,2007,35(10):80 -83.
LIU Qiong,YE Jing-jing,SHAO Xin-yu.Design of logistics networks for manufacture/remanufacture in uncertain environment[J].Journal of Huazhong University of Science and Technology,2007,35(10):80 -83.
[10]张 勇,蒋 琦.不确定环境下的物流配送中心选址方法研究[J].兰州交通大学学报,2007,26(1):135-137.
ZHANG Yong,JIANG Qi.Logistics distribution center allocation medel and algorithm in uncertain environments[J].Journal of Lanzhou Jiaotong University,2007,26(1):135-137.
[11]胡承毅,徐山鹰,杨晓光.区间算法简介[J].系统工程理论与实践,2003(4):59-62.
HU Cheng-yi,XU Shan-ying,YANG Xiao-guang.A brief introduction to the interval methods[J].System Engineering Theory and Practice,2003(4):59-62.
[12]Moore R,Yang C.Interval analysis,LMSD - 285875[EB/OL].California:Missiles and Space Division,Lockheed Aircraft Corporation,1959[2011 -06-12].http://interval.Louisiana.edu/Moores_early_paper/Moore_Yang.pdf.
[13]Csallner A E,Csendes T.The convergence speed of interval methods for global optimization[J].Computers &Mathematics with Applications,1996,31(4 - 5):173 -178.
[14]Kasperski A,Zielinski P.An approximation algorithm for interval data minmax regret combinatorial optimization problems[J].Information Processing Letters,2006,97(5):177-180.
[15]Jiang C,Han X,Liu G R,et al.A nonlinear interval number programming method for uncertain optimization problems[J].European Journal of Operational Research,2008,188(1):1 -13.
Interval decision-making model and algorithm for continuous logistics facility location
LI Li-hua1,2,FU Zhuo1,HU Zheng-dong1,3
(1.School of Traffic and Transport Engineering,Central South University,Changsha 410075,China;2.School of Traffic and Transport Engineering,Changsha University of Science and Technology,Changsha 410004,China;3.School of Political Science and Public Administration,University of South China,Hengyang 421001,China)
In this paper,the uncertainty of logistics demand is considered.The interval number is used to measure uncertain parameters and variables.The interval decision-making model for continuous logistics facility location with multi commodity and multiple nodes is established.The properties and size of interval solution is judged by interval possibility,and the interval interactive genetic algorithm is designed to solve the problem.It is showed by a tested example that the research results have strong practical operability,and the method can be offered as an alternative for decision making for location of logistics node.
logistics facility location;interval decision;uncertainty;gravity method;genetic algorithm
U495
A
1672-7029(2011)06-0107-07
2011-12-07
国家自然科学基金资助项目(70671108);湖南省科技计划项目(2010FJ6016)
李利华(1979-),男,湖北红安人,讲师,博士研究生,从事交通运输规划与管理研究
