某多管火箭炮车炮刚柔耦合极限路况行驶动力学研究

任 杰， 秦 伟， 马大为， 李志刚

(南京理工大学 机械工程学院，南京 210094)

车载多管防空火箭炮行军时需能通过各种恶劣的道路，具备通过垂直台阶、水平壕沟、陡坡等障碍的能力，研究其通过障碍的能力和通过障碍时的动态特性非常重要。车载多管火箭炮通过路面障碍的能力直接影响其作战性能，而通过障碍所引起的振动则是影响武器寿命和安全的一个重要因素，通过障碍时引起的振动不仅会导致零部件过早的磨损、疲劳和损坏，还会给乘员带来疲劳甚至损害健康，最终影响武器的正常使用。这就要求研制的车载多管防空火箭炮必须按照相应的标准进行路面试验，在研制过程进行行驶动力学仿真分析可以获知一部分关键参数，有助于设计的改进，避免样机的重复制造，节省了研制时间和经费。

目前，行驶动力学的主要研究对象为车辆，很少考虑武器系统，多采用多刚体系统动力学理论进行研究［1－4］，近年来引入了柔性多体系统动力学理论［5，6］。多管火箭炮动力学的研究主要以发射动力学为主，关心其发射时的动态响应特性，南京理工大学芮筱亭［7，8］应用多体系统传递矩阵法对多管火箭炮发射动力学做了大量研究工作。而车载多管火箭炮车炮系统复杂，行驶动力学研究并不多见，主要采用大量路面试验进行研究。本文与以往研究有较大区别，主要以多刚体系统动力学和柔性多体系统动力学理论为基础，考虑了越野车、多管火箭炮和路面障碍，建立了相对完整的刚柔耦合车炮动力学模型进行研究，能获得较为准确的结果，为工程研制、试验提供一定的理论支持。

1 基本理论研究

研究刚柔耦合多体系统动力学问题，需将多刚体系统动力学和柔性多体系统动力学基本理论相结合。

有限元法处理柔性多体动力基本学思路是，将柔性体离散化，以离散后若干个单元的有限个节点自由度来去表示物体的无限多个自由度，单元的弹性变形可用少量模态的线性组合近似的表示。

如果物体在坐标系的位置用它在惯性坐标系中的笛卡尔坐标X=(x，y，z)和反映刚体方位的欧拉角Ψ=(ψ，θ，φ)来表示［9］，模态坐标用 q={q1，q2，…，qm}M(M为模态坐标数)来表示，则柔性体的广义坐标可选为:

柔性体的动能表达式为［10，11］:

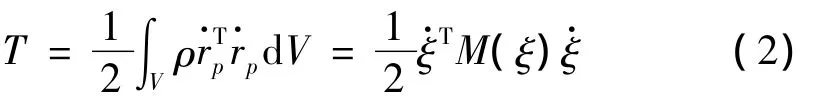
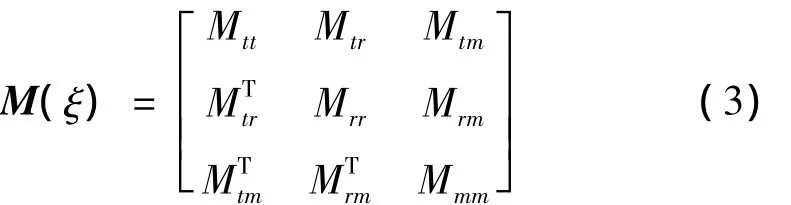
最后运用拉格朗日乘子法建立柔性体的运动微分方程:

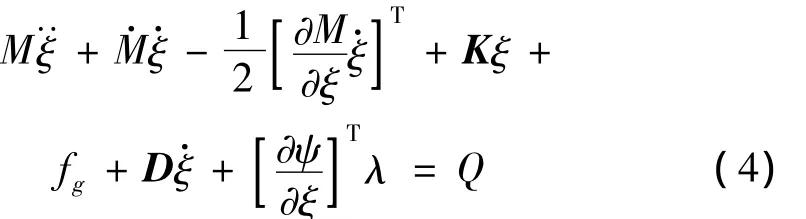
式(4)中，K为模态刚度矩阵;D为模态阻尼矩阵;Kξ和D分别为物体内部由于弹性变形和阻尼引起的广义力;fg为广义重力;λ为对应于约束的拉格朗日乘子;Q为对应于外力的广义力。

2 车载多管火箭炮刚柔耦合模型的建立

2.1 车载多管火箭武器系统的结构

车载多管火箭炮结构较为复杂，其结构如图1所示。

经合理简化后建立刚柔耦合的车炮多体动力学模型，模型主要包含:驾驶室、底盘(包括车大梁、板簧、铰接件)、轮胎、底座、回转支承、发射箱、定向器、火箭弹等构件。

图1 车载多管火箭炮结构示意图Fig.1 The structural diagram of the multiple launch rocker system in vehicle

2.2 多管火箭武器系统的多体系统动力学描述

将车载多管火箭炮简化成n个刚体组成的多体系统。将驱动桥、驾驶室、车大梁、底座、回转支撑、起落架、发射箱、定向器和弹分别设为刚体。对任意多体系统的拓扑构型表达方式而言，个体记为Bi(i=1，2，3，…，n)，n为系统中体的个数，用连接邻接体的有向线段表示铰，记为 hj(j=1，2，3…)。B0表示系统外运动为已知的体;铰的指向背离B0方向;车载防空火箭武器系统的拓扑结构如图2所示。

图2 系统拓扑结构Fig.2 The topological structure of system

本文采用RecurDyn软件进行行驶动力学分析。为描述系统的运动，需建立惯性坐标系和各物体基点坐标系，所建立的坐标系均为右手直角坐标系。首先建立惯性坐标系o0x0y0z0，以大梁上平面中心线与最外面边线的交点处为原点o0，x0轴正方向与车行进方向相反，z0轴垂直向上。然后分别建立大梁坐标系()、底座坐标系()、回转台坐标系()、起落架坐标系()、定向管坐标系、一枚弹坐标系()、前驱动桥坐标系()、后驱动桥坐标系()。各坐标系原点均在质心位置处，x轴正方向均为与车行进方向相反，Z轴均垂直向上。各坐标系均固结在对应构件上，随之运动。

车载多管火箭炮通过路面障碍时，车体大梁的变形对系统影响不可忽略，模型中需考虑大梁的柔性效应，故将其建为柔性体，使用有限元软件建模，再导入RecurDyn中替代多刚体动力学模型中的刚性大梁，并定义相应的连接节点，建立刚柔耦合的动力学模型。

轮胎采用Fiala轮胎模型，无量纲表达式为［12］:

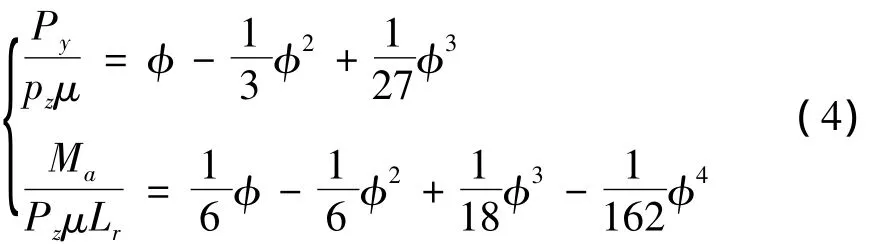
式(4)中，Py为轮胎侧偏力;Ma为回正力矩;μ为附着系数;Pz为垂直载荷;Lr为轮胎印迹长度;φ为无量纲侧偏角，且 φ =Ktgα/(Pzμ)，K 为轮胎侧偏刚度，α为轮胎侧偏角。

2.3 含垂直凸台路面模型的参数确定

越野车超越垂直凸台或阶状障碍的能力主要取决于其所能克服的垂直障碍的极限高度。

图3为超越阶状障碍瞬间越野车受力示意图。N1、N2分别为地面对前、后车轮的反作用力，μN1、μN2分别为前、后车轮与地面接触点处的推力，W为整车重量的一半，α为前轮上的反作用力与水平面的夹角，h为垂直台阶的高度，h0为车重心到车轴平面的垂直距离，a为前轴至车重心的水平距离，r为车轮半径，l为车轴距。

图3 越野车前轮超越阶状障碍Fig.3 The state of vehicle when the front wheels passing over the step obstacle

由图3可列出整车垂直方向、水平方向的力平衡方程式以及对前轴的力矩平衡方程式:

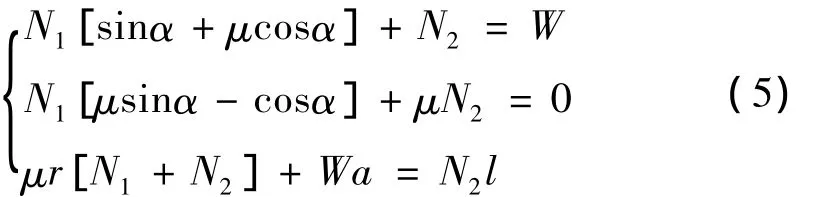
解得前轮可超越障碍高度的无因次表达式为:

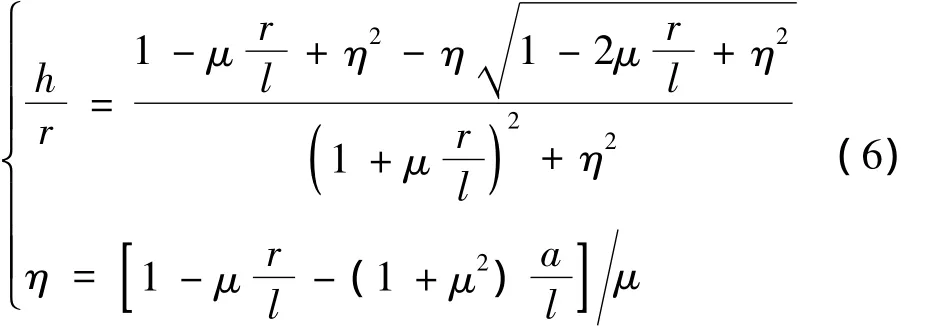
式(6)中，a取1700 mm;μ取0.8(车轮与硬路面的附着系数);r取 560 mm;l取 3400 mm。解得 h=358.42 mm。

车后轮开始超越阶状障碍时，受力如图4所示，α为后轮上的反作用力与水平面的夹角，车身呈β度倾斜，其余符号标示与图3一致。

图4 越野车后轮在超越阶状障碍Fig.4 The state of vehicle when the rear wheels passing over the step obstacle

由图4可列出整车垂直方向、水平方向的力平衡方程式以及对后轴的力矩平衡方程式:

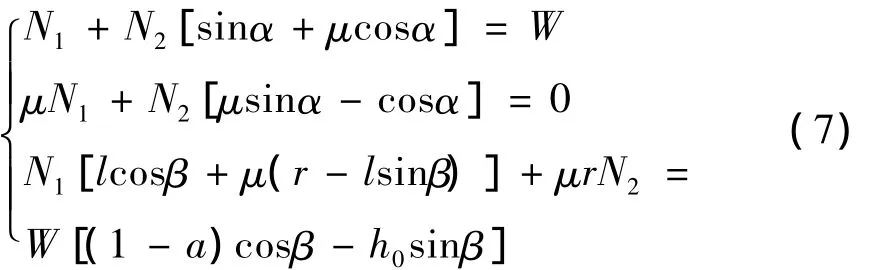
解得 h=290.3 mm。

解得前、后轮可通过的台阶极限高度后取较小的h值，故设定垂直凸台的高h为290 mm，长为300 mm。

2.4 含壕沟障碍路面模型的参数确定

壕沟宽度ld与车轮直径D和轴距l等几何参数有关。Bekker认为，对同一轮式车辆，若已知h/D值，可通过h/D和ld/D的关系曲线(如图5所示)来确定极限壕沟宽度 ld［13］。由上文可知，h=290 mm，D=1120 mm，由图5中的曲线关系可得ld/D=0.85，壕沟极限宽度ld为952 mm，参考GJB 349.13A － 1997《火箭炮定型试验规程》，可取壕沟宽度为300 mm＜952 mm。

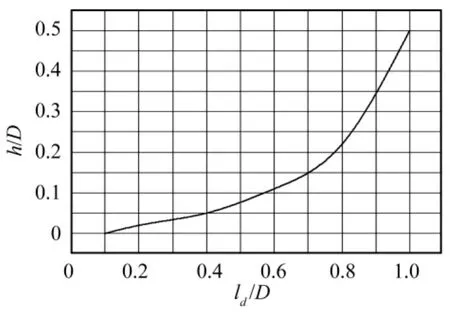
图5 h/D和ld/D关系曲线Fig.5 The relationship curve of h/D and ld/D

2.5 含陡坡路面模型的参数确定

越野车通过陡坡时，首先要考虑进入陡坡时接近角和离去角的极限位置，需和地面无干涉，防止出现触头失效和拖尾失效。其次要考虑从陡坡出来时，要求陡坡和越野车无干涉，防止出现顶起失效。文中越野车的接近角为36°，离去角为35°，考虑行军时为带弹全负载，取坡道的坡度为60%，坡道长20 m，坡前为平直路面。

2.6 约束条件与激励源

车载多管火箭武器系统在行驶过程中，火箭炮上装部分将由行军固定器固定，在模型中相应位置施加对应的约束条件。

行军过程中系统的主要激励来源于路面不平、轮胎和传动轴及发动机等。一般认为，路面不平引起的垂直方向加速度是多管火箭武器系统系统振动的主要因素。在越障行军过程中，主要考察各种路面障碍对系统的影响，研究时假设动力总成等不产生振动，主要激励来自路面障碍，垂直方向的激励按路面—车体—炮身路径传递。

3 刚柔耦合多管火箭炮行驶动力学仿真研究

对越障行驶时的车载多管火箭炮进行行驶动力学仿真研究，需重点考察系统的垂向加速度、垂向加速度功率谱密度、侧向加速度以及炮质心处的摆动加速度，获取车载多管火箭炮通过路面障碍时的关键参数响应。

3.1 垂直凸台路面行驶仿真分析

经过多次仿真，认为以12km/h的车速通过垂直凸台障碍时系统的动态响应较为理想，故本次分析设定越野车以12km/h的速度行驶，四轮驱动越过垂直凸台，考察车炮系统的垂向加速度、垂向加速度功率谱、侧向加速度、横摆角速度等关键参数的动态响应。

由图6可知，当车遇到垂直凸台时，产生垂向和侧向的加速度。前轮接触垂直凸台时，整个系统重心靠后，柔性大梁变形不大，火箭炮质心加速度值小于全系统质心加速度值，火箭炮质心加速度峰值约为5.3 g，系统质心的加速度峰值约为9.2 g;后轮接触垂直凸台时，柔性大梁产生较大的变形，使得火箭炮的加速度较大，系统质心的垂向加速度峰值约为9.2 g，而火箭炮质心垂向加速度峰值约为14 g。当前、后车轮越过垂直台阶后，加速度均能够快速稳定下来。

由图7～图9可知，通过垂直台阶时的侧向加速度、横摆角加速度等响应变化范围和峰值均不大，整体加速度的功率谱密度峰值较小，最大值发生在9 Hz处，其值约为28 mm2/s3。仿真表明车炮系统在通过垂直台阶时较稳定，车轮接触台阶瞬间垂向加速度值变化较大。

3.2 含壕沟障碍路面行驶仿真分析

越野车四轮驱动、以12km/h的车速驶过水平壕沟。由图10可知，当越野车前轮进入壕沟时，垂向加速度开始出现负值，前轮到达最低点开始爬升，垂向加速度迅速增大到最大，其值约为3.8 g。后轮进入和离开壕沟时垂向加速度变化规律类似，但幅值小于前轮，最大值约为3 g。

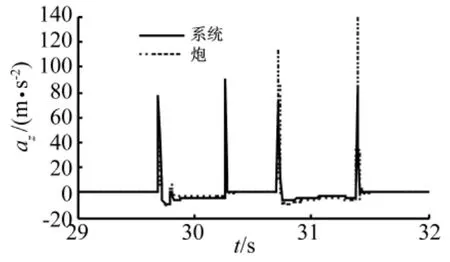
图6 系统质心与炮质心垂向加速度对比Fig.6 The centroid vertical acceleration of rocket launcher and whole system

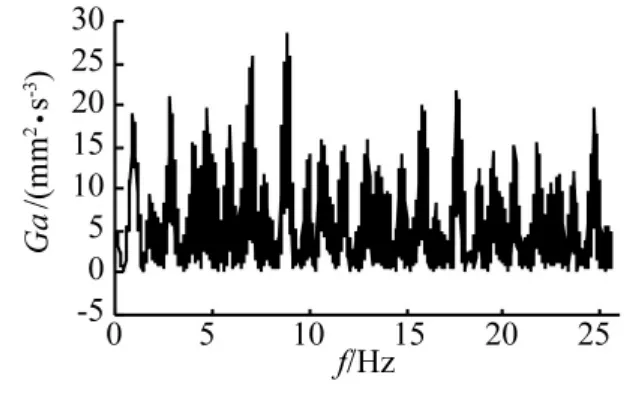
图7 行驶过程垂向加速度功率谱密度Fig.7 The power spectral density of vertical acceleration during the running

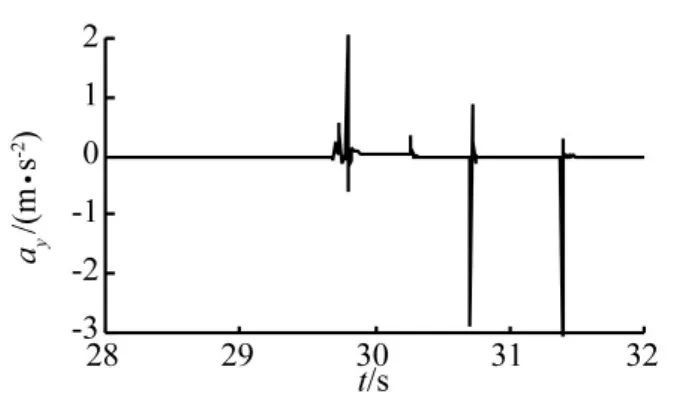
图8 系统质心侧向加速度Fig.8 The lateral acceleration of system centroid

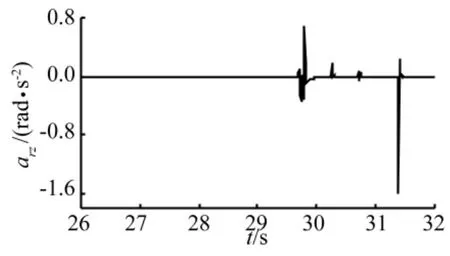
图9 系统质心横摆角加速度Fig.9 The lateral oscillating angular acceleration of whole system centroid

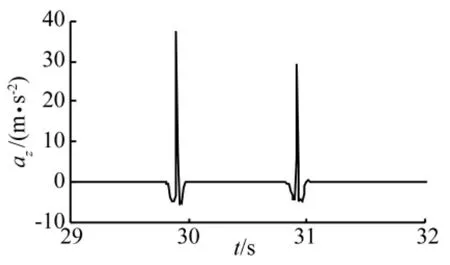
图10 系统质心垂向加速度Fig.10 The vertical acceleration of system centroid

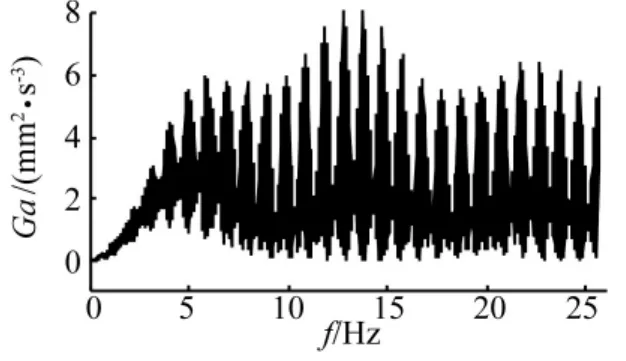
图11 行驶过程垂向加速度功率谱密度Fig.11 The power spectral density of vertical acceleration during the running

由图11～图13可知，系统质心垂向加速度的功率谱密度峰值较小，峰值出现在13 Hz处，约为8 mm2/s3;驶过水平壕沟时系统质心的侧向加速度不大，峰值为0.14 m/s2，出现在后轮通过壕沟时。横摆角加速度峰值为0.042 rad/s。

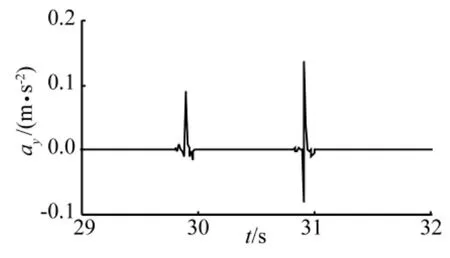
图12 系统质心侧向加速度Fig.12 The lateral acceleration of system centroid

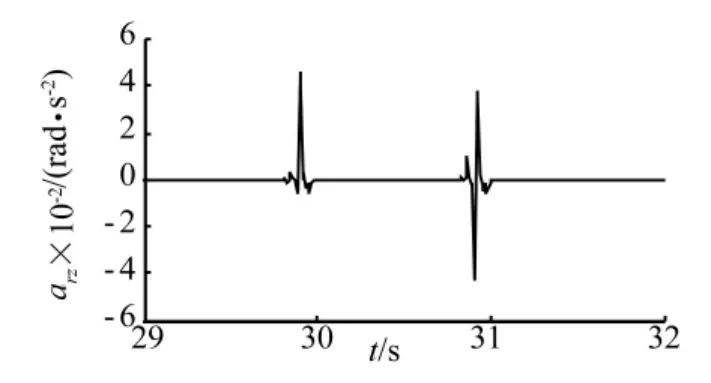
图13 系统质心横摆角加速度Fig.13 The lateral oscillating angular acceleration of system centroid

结果表明，此车载多管火箭炮以12km/h的速度通过含水平壕沟的道路较平稳，各项关键参数响应均不大。

3.3 含陡坡路面行驶仿真分析

陡坡坡度为60%，通过多次仿真计算得出16km/h的车速下通过该陡坡响应较为理想，故仿真时取车速为16km/h，采用四轮驱动，进行计算，结果如下。

由图14～图15可知，车前轮进入和驶出陡坡时，垂向加速度值出现峰值，分别为7.8 g和5.6 g。后轮进入和驶出陡坡时的垂向加速度比前轮小得多。车驶出斜坡时后轮出现腾空，如图16所示。

由图17～图19可知，系统质心垂向加速度的功率谱密度峰值较小，峰值出现在6 Hz处，约为3.5 mm2/s3;车前后轮进入和驶出陡坡时出现侧向加速度，前轮进入陡坡时侧向加速度最大值为0.39 mm/s2，驶出陡坡侧向加速度比进入时要大，峰值为0.65 mm/s2;后轮进入陡坡时的侧向加速度比前轮进入时小，峰值为0.19 m/s2，驶出斜坡时呈腾空的状态(图16所示)，落地时侧向加速度最大为0.3 mm/s2。系统质心横摆角加速度幅值较小。表明车炮系统以16km/h的速度通过该陡坡较稳定。

图14 进入陡坡时系统质心垂向加速度Fig.14 The vertical acceleration of system centroid during driving up steep gradients

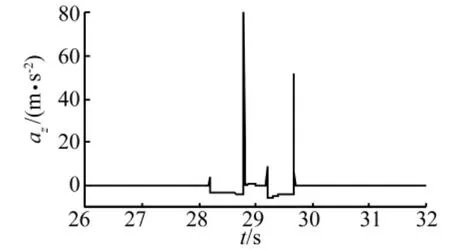
图15 离开陡坡时系统质心垂向加速度Fig.15 The vertical acceleration of system centroid during away from steep gradients

图16 后轮驶出陡坡腾空状态Fig.16 The state of the rear wheels when driving up steep gradients

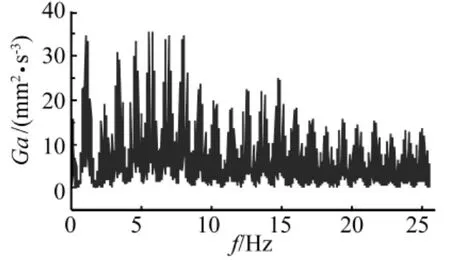
图17 行驶过程垂向加速度功率谱密度Fig.17 The power spectral density of vertical acceleration during the running

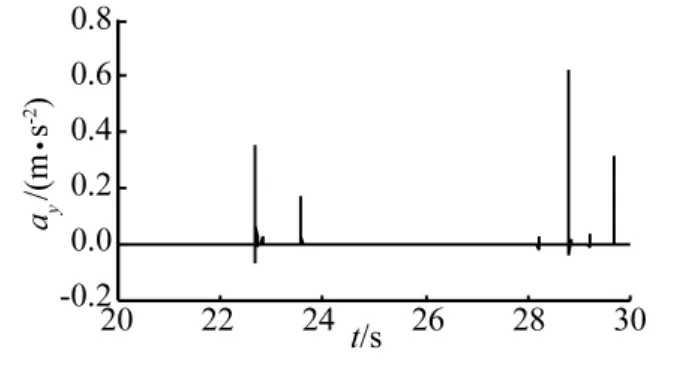
图18 系统质心侧向加速度Fig.18 The lateral acceleration of system centroid

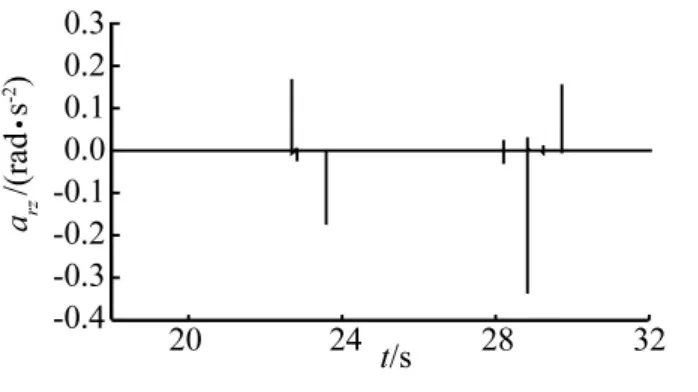
图19 系统质心横摆角速度Fig.19 The lateral oscillating angular acceleration of system centroid

4 结论

文中根据车炮系统的实际情况计算了前、后轮通过垂直凸台的极限高度和通过水平壕沟的极限宽度，依据试验要求和相关文献分别确定和建立了含垂直台阶、壕沟、陡坡等路面障碍的道路参数和模型，进行行驶动力学仿真分析后得到了一些有用的结论。

(1)通过垂直凸台障碍路面。车前轮接触垂直凸台时，柔性大梁变形不大，火箭炮质心在全系统重心之后，使火箭炮质心加速度值小于全系统质心加速度值;后轮接触垂直凸台时，柔性大梁变形较大，使大梁上火箭炮的垂向加速度大于系统质心的垂向加速度;车轮越过垂直台阶后，加速度均能够很快地稳定;全系统垂向加速度的功率谱密度、侧向加速度、横摆角加速度等响应变化范围和峰值均不大。

(2)通过水平壕沟路面。车前轮接触水平壕沟边缘时，垂向加速度出现负值，前轮到达最低点时，垂向加速度由负值迅速增大到正向最大值;后轮进入和离开壕沟时垂向加速度变化规律类似，全系统质心垂向加速度的功率谱密度、侧向加速度、横摆角加速度等各项幅值关键参数响应均不大。

(3)通过陡坡路面。全系统的垂向加速度峰值出现在前后轮进入和驶出陡坡时，后轮进入和驶出陡坡的垂向加速度比前轮小得多，而驶出陡坡时后轮会腾空。前轮进入陡坡时的侧向加速度幅值要小于驶出陡坡时;后轮进入和驶出陡坡时的侧向加速度比前轮小，系统质心垂向加速度的功率谱密度、侧向加速度和横摆角加速度均不大。

(4)仿真表明，垂向加速度功率谱主要分布在低频段，路况差加速度响应的功率谱值就高。通过垂直凸台路面，系统质心垂向加速度的功率谱密度峰值9 Hz，幅值为28 mm2/s3;通过水平壕沟路面，系统质心垂向加速度的功率谱密度峰值13 Hz，幅值为8 mm2/s3;通过垂直凸台路面，系统质心垂向加速度的功率谱密度峰值 6 Hz，幅值为 3.5 mm2/s3;

(5)越野车通过路面障碍时，会产生附加的侧向加速度，侧向加速度幅值要远小于垂向加速度幅值。

［1］Christensen D E.Multiple rocket launcher characteristics and simulation technique［R］.USA:AD-A025379，1976.

［2］Karnopp D.Active damping in road vehicle system［J］.Vehicle System Dynamics，1983，12:291 －311.

［3］维腾伯格.多刚体系统动力学［M］.北京:北京航天航空大学出版社，1986.

［4］Huston R L.Kane's equations with undetermined multi-pliers application on constrained multibody systems［J］.ASME Journal of Applied Mechanics，1987，54:424 －429.

［5］Juang J N，Horta L G.Effects of atmosphere on slewing control of a flexible structure［J］.Journal of Guidance control and Dynamics，1987，10(4):387 －392.

［6］Ho J Y L.Direct path method for flexible multibody spacecraft dynamics［J］.Journal of Spacecraft and Rocket 1977，14(2):102 －110.

［7］芮筱亭，陆毓琪.多体系统振动的传递矩阵法［J］.宇航学报，1995，16(3):41－47.

［8］王国平，芮筱亭.远程多管火箭动力学研究［J］.动力学与控制学报.2004，2(1):59－64.

［9］刘延柱.完全笛卡尔坐标描述的多体系统动力学［J］.力学学报.1997，29(1):84－94.

［10］陆佑方.柔性多体系统动力学［M］.北京:高等教育出版社，1996.

［11］冯 勇，马大为，薛 畅.多管火箭炮刚柔耦合多体发射动力学仿真研究［J］.兵工学报，2006，(3):545－548.

［12］屈求真，刘延柱.汽车轮胎侧偏特性的研究现状及其发展［J］.上海交通大学学报，1999，33(6):755－759.

［13］Bekker M G.Off-the-Road Locomotion［M］.University of Michigan Press，1960.