地铁列车振动对精密仪器影响的预测研究

马 蒙，刘维宁，丁德云，Degrande G，刘卫丰

(1.北京交通大学 土木建筑工程学院，北京 100044;2.鲁汶大学 土木工程系，比利时)

目前，北京城市轨道交通建设已进入蓬勃发展的时期:截至2008年，已开通运营的线路达8条，总里程达到199.6km;规划到2015年，将建成19条线路共561km的轨道交通网［1］。然而，地铁的大规模建设将对沿线的歌剧院、医院、古建等敏感建筑以及设有高精密度仪器仪表的科研院所产生严重影响［2－5］。其中，轨道交通列车引起的振动对精密仪器设备的影响已经成为一个世界性难题:如台湾新干线穿越台南工业科学园(TNISP)［6］，亚特兰大已建成的地铁线路上方拟建医疗建筑［7］，华盛顿大学物理天文实验室楼受到轻轨交通线路的潜在低频影响［8］等。近年来，北京地铁建设对科研单位的影响日益突出。例如，地铁4号线近距离经过北大物理实验楼;地铁10号线沿线经过中国空间技术研究院、中科院微电子所等振动敏感区域;地铁15号线规划下穿清华大学校园，也将近距离经过具有精密仪器的实验室。当地铁列车引起的振动过大时，会影响仪器仪表刻度阅读的准确性和阅读速度，严重时无法读数甚至可能损害和破坏仪器仪表。因此，在前期线路规划和环境评价时如何准确预测地铁通车运营后对精密仪器的影响以及评估减振措施的有效性便成为亟需解决的问题。

地铁隧道建成通车前，数值模拟是进行振动预测的一个重要手段。然而，由于参数确定、计算机时等因素的限制，很难在数值模型中同时考虑建筑物、实验台等因素;但建立相应的隧道－地层模型，并预测自由场地振动响应的方法已趋于完善。基于此，本文以北京某新建地铁线路近距离经过某科研机构为背景，预测未来地铁列车振动对楼内精密仪器的影响。利用周期性边界元－有限元耦合模型计算得到自由场地条件下实验楼外地表拾振点处的振动响应;其次，在现场进行了环境振动测试，获得了精密仪器实验台与楼外地表拾振点的现况振动数据，并以此计算出两点间的振动响应传递比;最后，通过该实测传递比将数值计算所得的楼外振动响应折算到实验台上，以达到预测的目的。

1 现场振动测试

现场振动测试是本文预测方法中的重要环节。振动由地层经建筑物传到实验台上，在此传播路径中，大部分频段的振动量会得到衰减;但受建筑基础、楼板、实验台等结构固有频率影响，相关频段也可能被放大。因此，通过测试，可以获得现况背景下楼外测点与实验台之间在不同频段上振动衰减程度或放大程度(本文采用“振动响应传递比”表示)。同时，实验台面上的测试数据可以直接反映精密仪器的现况振动水平，以此判断与允许振动量相比仪器是否超标、或探知现存振动余量水平。

1.1 测点布置

拟建地铁区间隧道采用盾构法施工，盾构外径为6 m，轨面埋深20 m，隧道结构中心线距离该科研大楼外墙最近处13.7 m。在实验室内及楼外分别布置测点(图1):楼外测点SW1位于地表未来地铁隧道中心线位置处;在108实验室内的三个实验台上分别布置三个测点，记作SN1、SN3、SN5。每个测点均测试了加速度、速度、位移三个响应量(均包括x、y、z三个方向)，每个方向测试10～13组数据。图2为一组典型时程、频谱图。

测试仪器采用LC0130T系列压电式加速度传感器，配套使用高速便携式数据采集器Wavebook/516E/WBK18和LC0205－8双积分信号调理器。

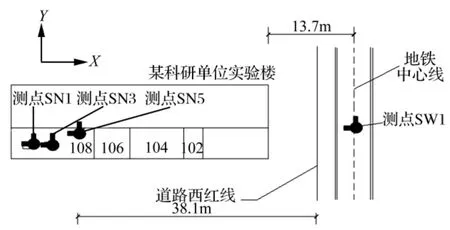
图1 测点布置示意图Fig.1 A schematic illustration of measuring points arrangement

图2 测点SN1现况背景的竖向速度时程图与频谱图Fig.2 Time history and frequency spectrum of vertical velocity on measuring point SN1

1.2 精密仪器允许振动要求

无论是对现况环境振动的评价还是对未来地铁列车振动的预测都需要比照精密仪器的允许振动要求。通常来讲，确定某一精密仪器的允许振动指标时，需要回答以下三个问题［9］:(1)数据表达的分析域(即时域还是频域);(2)衡量单位(即位移、速度还是加速度);(3)统计形式(瞬时值还是平均值)。国际上对于精密仪器允许值使用何种分析域存在较长时间的争议［9－15］。但在 1995 年以后，1/3 倍频程标准被广泛采用。

目前，国际上一般采用文献［14］提出的容许速度标准，该标准把精密仪器防微振动划分为五个等级(表1)，该标准的允许量值为1/3倍频下的振动速度均方根值。

通过对本文所研究的实验室内各种精密仪器类型、精度及已知允许振动量值的调查与分析:室内绝大部分仪器的允许振动量值介于表1所示VC－C级与VC－D级之间，最精密的仪器振动要求已达到VC－D级。为此，下文将以VC－C级和VC－D级作为实验台的振动控制标准。

表1 精密仪器允许振动量的一般规定Tab.1 Generic vibration criterion

1.3 现况振动评价

将现况环境振动测试结果与仪器允许振动要求进行比较(图3)可以发现，由于距楼外道路水平距离的不同以及实验台自身隔振条件的差异，SN1、SN3两点的现况均能满足仪器正常工作，且余量分别介于68.8% ～84.8%和31.7% ～67.2%;而在 SN5 测点处，当楼外道路有卡车、公交车经过时，不采取被动隔振措施已无法确保最精密的仪器正常工作(这与目前仪器实际工作状况相吻合)。

1.4 振动传递比计算

振动在土体、建筑物内传播时，由于受到辐射阻尼、材料阻尼等因素影响，振动总体呈现衰减趋势，但受建筑结构自振特性影响，部分频段有可能会被放大。目前在进行建筑物内振动环境评价时，通常假定:两点间的振动衰减只与建筑物的本身特性(包括建筑物基础型式、结构型式、建筑材料地板的隔振型式等)有关，而与振源的位置无关。基于此，为研究不同频段振动传递的放大或衰减程度，本文引入振动响应传递比(简称“传递比”)的概念。实验台某测点与楼外SW1测点之间的传递比表示为:

图3 室内各测点现况环境振动水平Fig.3 Vibration velocity on sensitive instrument tables

式中X(fi)为实测楼外的(SW1)振动响应，Y(fi)为实测室内的(SN1、SN3或SN5)振动响应，两点响应均为1/3倍频程下的量值，下标i表示每一频带对应的中心频率。当某频段传递比小于1时，振动呈衰减趋势;反之，该频段的振动响应被放大。

当利用数值模拟获得地铁列车运营时自由场地处某点的振动响应，则可以利用(1)式将楼外振动量折算到实验台上。假设数值模拟预测得到地铁运行时SW1点处振动响应为X'(fi)，则地铁引起的振动折算到实验台上的响应Y'(fi)可以表示为:

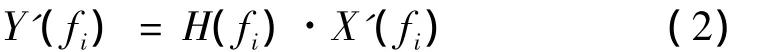
图4 室内三个测点与SW1点之间的传递比曲线Fig.4 Vibration transfer ratio between SW1 and SN1/SN3/SN5

图4为基于现况实测数据、并根据(1)式计算得到的室内三个测点与楼外SW1点之间的竖向(Z向)速度传递比曲线。图中，散点代表实际计算结果，曲线为高次多项式拟合结果;拟合后的曲线可以较准确地反映各频带对振动衰减作用(或放大作用)的趋势，从而避免传递比在个别频带偏差过大带来的误差。可以发现，楼外与室内测点间振动主要呈现衰减趋势，但建筑结构及实验台自振特性会导致部分频带的响应放大。以往大量测试结果表明，地铁列车引起的地面振动主要频率在30 Hz～80 Hz，SN1、SN3两点在该频段可获得较好的振动衰减效果，但SN5点在接近100 Hz时有一个振动相对放大峰值，传递比超过0.7，衰减作用不明显。未来地铁列车振动影响将有可能出现在此频段。

2 数值计算

为了考虑列车沿线路通过时的纵向时空效应，并避免单纯采用三维动力有限元法所消耗的大量计算时间，本文选用周期性有限元－边界元耦合方法［16］。该方法遵从以下假定:(1)地铁线路为直线，隧道结构在其轴线方向ey上具有周期性和一致性;(2)隧道埋置在水平成层的半无限土体介质中;(3)位移和应变足够小，满足线性叠加原理。根据以上假设，建立轨道－隧道－土体相互作用模型，利用积分变换在频域－波数域内求解。

2.1 移动荷载作用下的动力响应

地铁列车运行可看做一系列移动轴荷载作用于钢轨上，如图5［17］所示，第k个移动轴荷载可以表示为用来确定荷载位置的Dirac函数和第k个轴荷载幅值的乘积，而第na个列车轴荷载则可以表示为:

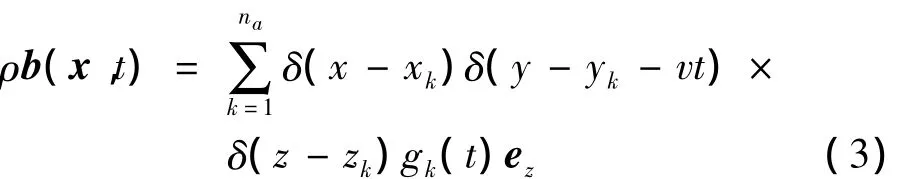
其中，yk是第k个轴荷载的初始位置，v为列车沿y轴车速，ez为竖向单位向量。

图5 地铁隧道内的列车移动荷载示意图Fig.5 Axle loads inside the tunnel

对式(3)进行Fourier变换，得到频域内表达式:

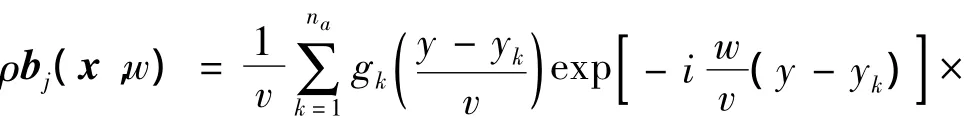
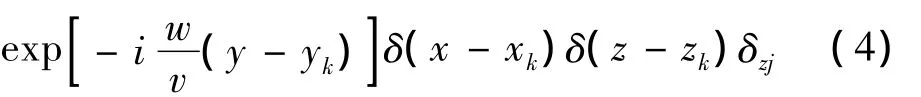
其中，顶划线“^”表示频域内的函数。na个列车轴荷载作用下，拾振点x在频域内响应可以写作:

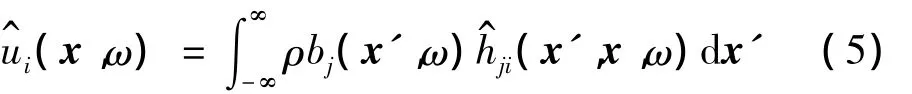
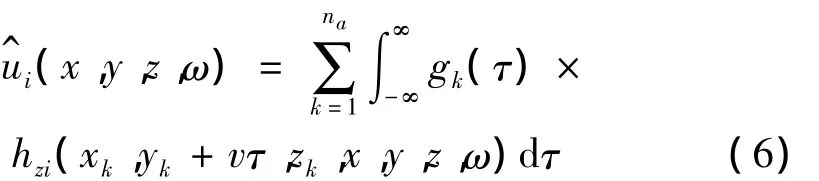
如果隧道－自由场动力相互作用系统在隧道轴线方向具有周期性，可以利用Fourier变换和Floquet变换将式(6)进一步简化为［16－19］:

2.2 计算参数及传递函数

按照规划设计，盾构管片每一环由6片组成，纵向由螺栓连接，管片混凝土衬砌的杨氏模量Et=35000 MPa，泊松比 νt=0.25，密度 ρt=2500 kg/m3，滞回材料阻尼比βt=0.02。隧道仰拱处灌注混凝土道床，其杨氏模量 Et=28500 MPa，泊松比为 νt=0.2，密度为 ρt=2500 kg/m3，滞回材料阻尼比为 βt=0.02。轨道中采用北京地铁常用的DTVI2扣件。根据地质勘探报告，将该处地层简化为5层，各层土动力参数见表2。

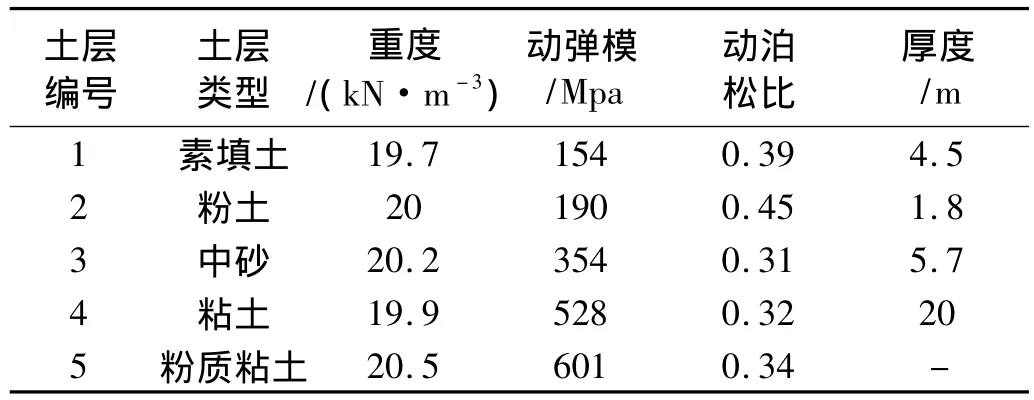
表2 土层动力参数表Tab.2 Dynamic soil characteristics

利用三维周期性有限元－边界元耦合数值模型可求解传递函数。其中，采用有限元法建立隧道模型、边界元法建立土层模型，并在土结界面上耦合。利用有限元软件MIDAS/GTS建立隧道基本单元模型，见图6。根据模态叠加原理，隧道上位移场可表示为:

图6 隧道基本单元有限元模型Fig.6 Finite element model of the generic cell of the tunnel

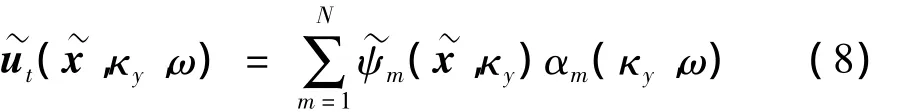
而在频率－波数域内的隧道－自由场动力相互作用方程可以写作［4，16，20］:

其中，Kt(κy)、Mt(κy)为隧道基本单元的动力刚度矩阵和质量矩阵，Ks(κy，ω)为土层基本单元的刚度矩阵。在频域－波数域中解方程(10)，求出模态坐标并代入式(8)、式(9)即可求得基本元内隧道结构中及土结界面上的位移响应。再通过动力学互易定理和边界元的概念，最终可计算出土层中任意点的位移。

2.3 移动外荷载［4，20］

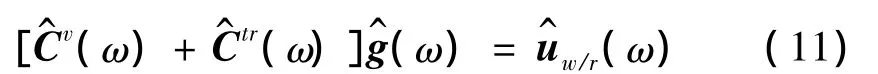
2.4 地表振动预测

地铁列车在其SW1点处引起的竖向振动响应要远大于其他两个水平方向的响应，因此下文主要分析竖向预测结果，水平方向预测方法与此相同。考虑不同的列车行车速度(30km/h、45km/h、60km/h、80km/h)，最终可获得SW1点的振动速度预测结果(图7)。可见，地铁在地面最主要的影响集中在40 Hz～80 Hz的中高频段，且列车车速直接影响该频段峰值。

图7 不同车速地表振动响应结果Fig.7 Vibration results under different train speeds on the ground detecting point

3 仪器实验台预测与分析

利用式(3)可将楼外SW1点的数值预测结果(图7)通过传递比曲线(图4)折算到室内各测点，从而获得地铁列车运行下各实验台上的振动响应预测值。

由于未来地铁开通运营后，仪器会受到地面公交车流与地下列车振动的双重影响，故需综合考虑两种振源的作用。式(12)对每一频段的均方根值进行了叠加。

式中，vfe为实验台环境振动响应的现场实测值，vfm为地铁列车单独作用对实验台振动响应的预测值，振动叠加后的结果见图8。可见，如果未来地铁列车高速运行通过，所分析的三个实验台上精度最高的仪器均无法正常工作;SN5点由于其所处位置和实验台条件相对较差，车速降至60km/h依旧难以满足仪器要求。降低车速、匀速运营可以确保竖向振动响应控制在仪器允许振动要求之内。

图8 实验台上竖向振动速度预测结果Fig.8 Prediction of vertical velocity on sensitive instrument tables

4 结论与建议

本文以地铁引起的振动对某实验室内精密仪器影响为背景，采用周期性有限元－边界元耦合的数值模拟与现场实测相结合的方法，对仪器实验台上的振动做出预测。该方法可以考虑建筑结构、实验平台在不同频段下的振动吸收或放大作用;可分频段分析地铁列车引起的振动对精密仪器的影响，并在1/3倍频程频域下与国际通用的精密仪器防振要求进行比较。

现场实测表明:楼外道路上的车流造成实验台水平方向振动量过大，在测点SN5甚至超过最精密仪器的振动要求，建议采取相应被动隔振措施。

考虑不同车速匀速运营条件下实验台的振动响应，当地铁列车低速、匀速通过时，地铁引起的振动不会对仪器造成影响，但会给行车组织和运送能力带来困难;当列车以大于60km/h通过时，建议采用较高级别的轨道减振措施确保仪器正常工作。

［1］谢正光.新形势下北京地铁的运营管理实践与思考［J］.现代城市轨道交通，2008，6:5 －9.

［2］孙晓静，刘维宁，郭建平，等.地铁列车振动对精密仪器和设备的影响及减振措施［J］.中国安全科学学报，2005，15(11):78－81.

［3］栗润德，张鸿儒，刘维宁.地铁引起的地面振动及其对精密仪器的影响［J］.岩石力学与工程学报，2008，27(1):206－214.

［4］Gupta S，Liu W F，Degrande G，et al.Prediction of vibration induced by underground railway traffic in beijing［J］.Journal of Sound and Vibration，2008，310:608 －630.

［5］孙晓静.地铁列车振动对环境影响的预测研究及减振措施分析［D］.北京:北京交通大学，2008.

［6］Hirokazu，Takemiya.Field vibration mitigation by honeycomb WIB for pile foundations of a high-speed train viaduct［J］.Soil Dynamics and Earthquake Engineering，2004，24(1):69－87.

［7］Nelson J.Recent developments in ground-borne noise and vibration control［J］.Journal of Sound and Vibration，1996，193(1):367－376.

［8］Wolf S.Potential low frequency ground vibration(＜ 6.3 Hz)impacts from underground LRT operations［J］.Journal ofSound and Vibration，2003，267:651 －661.

［9］Amick H. On generic vibration criteria foradvanced technology facilities with a tutorialon vibration data representation［J］.Journal of the institute of environmental sciences，1997，5:35 －44.

［10］Kjell A.Response equivalent peak velocity-a new method for description of vibration environment for sensitive equipment in buildings［J］.Proceedings of SPIE-The International Society for Optical Engineering，1999，3786:118 －125.

［11］Gordon C G.. Vibration Prediction and control in microelectronics facilities［A］//Proceedings of Inter-Noise 96［C］，1996:149－154.

［12］Medearis K. Rational vibration and structural dynamics evaluations for advanced technology facilities［J］.Journal of the Institute of Environmental Sciences and Technology，1995，38(5):35.

［13］Amick H，Bui S K A.A review of several methods for processing vibration data［A］//Proceedings of International Society for Optical Engineering(SPIE)［C］，San Jose，CA:1991:253－264.

［14］Gordon C G. Generic criteria for vibration-sensitive equipment［A］//Proceedings ofSPIE Conference on Vibration Control and Metrology［C］San Jose，California，1991:71－85.

［15］Ungar E，Sturz H，Amick H.Vibration control design of high technology facilitie［J］.Journal of Sound and Vibration，1990，24(7):20－27.

［16］Degrande G，Clouteau D，Othman R，et al.A numerical model for ground-borne vibration from underground railway traffic based on a periodic finite element-boundary element formulation［J］.Journal of Sound and Vibration，2006，293(3－5):645－666.

［17］Ding D Y，Gupta S，Lombaert G，et al.The Prediction of Vibrations Induced by Underground Railway Traffic on Line 8 of the Beijing Metro［R］.Leuven:Katholieke University;Beijing:Beijing Jiaotong University，2008.

［18］Lombaert G，Degrande G，Clouteau D.Numerical modelling of free field traffic-induced vibrations［J］.Soil Dynamics and Earthquake Engineering，2000，19(7):473 －488.

［19］刘卫丰.地铁列车运行引起的隧道及自由场动力响应数值预测模型研究［D］.北京:北京交通大学，2009.

［20］刘卫丰，刘维宁，Gupta S，等.地下列车移动荷载作用下隧道及自由场的动力响应解［J］.振动与冲击，2008，27(5):81－84.