临时支撑卸载冲击对施工中弦支穹顶结构性能的影响研究

刘慧娟，罗永峰，杨绿峰

(1.广西大学 工程防灾与结构安全教育部重点实验室，南宁 530004;2.同济大学 土木学院建筑工程系，上海 200092)

1 前言

几乎所有大型复杂钢结构施工过程中都要使用临时支撑，作为施工过程中的主要受力构件，临时支撑的设计计算的重要性主要体现在以下几个方面:

(1)临时支撑承担了施工过程中大部分荷载，同时部分高耸的临时支撑会受到水平风荷载等不利荷载作用，一旦临时支撑破坏，尚未完全成型的主体结构部分往往会出现倒塌破坏等事故［1］。

(2)临时支撑为施工中的主体结构提供临时约束，主体结构在施工中的受力状态和正常使用状态会有很大区别，但设计中一般不考虑施工工况，仅按照使用阶段进行结构设计。因此从结构安全的角度来看，结构构件在施工过程中有可能破坏。

(3)结构安装过程中，需要临时支撑的辅助以满足构件精确定位、安装的要求，因此，需要考虑支撑自身刚度及受力变形的影响。

(4)临时支撑拆除卸载是一个逐渐进行的过程，在此过程中，结构边界条件、受力体系发生转变，内力进行重分布，主体结构和临时支撑相互作用，受力状态的变化在整个卸载过程中持续发生，而且很有可能出现局部内力突然增大甚至内力性质变化的不利情况，这就需要考虑受力变化带来的主体结构和临时支撑结构的安全性问题。

由此可见，在弦支穹顶结构的安装过程中，临时支撑体系发挥着十分重要的作用。临时支撑体系不但承担着施工阶段部分结构的自重及施工荷载，而且对于安装精度和施工的便利性也有重要的影响［2］，所以大跨度结构施工中临时支撑体系的安全性、稳定性及布置的合理性日益成为施工过程中分析计算的重要部分。

1.1 瞬态分析方法

对弦支穹顶结构而言，临时支撑布置以满足施工阶段的结构强度和稳定的要求为原则，没有固定的模式，以往实际施工中大部分采用满堂脚手架。临时支撑的拆除卸载一般可采用各支承点同步卸载和多级循环卸载等方式。通常大跨度结构各个支承点下降位移是不相等的，因此，同步卸载又分为同步等比例卸载和同步等值卸载两种方式。实际结构工程中，有时为了简便起见，将未脱离的临时支撑直接卸载。这在结构相对比较简单或刚度较大、临时支撑系统不是很复杂且受力不大的情况下，也不失为一种可用方法，但是对于像弦支穹顶结构这样非线性较强的超静定、半刚性结构来说，将临时支撑直接卸载是不妥当的。支承力在很短时间内减为零，对有质量的结构来说是一种随时间突变的荷载作用或突加荷载作用，根据结构动力学原理，可对结构进行瞬态动力分析来考虑惯性力和运动阻力的影响。瞬态动力学分析基本方程为

其中，各个参数的物理意义是:［M］— 质 量矩阵，［C］—阻尼矩阵，［K］—刚度矩阵，— 节 点加速度向量，{}— 节点速度向量，{u}— 节点位移向量，{F(t)}—随时间变化的荷载作用向量。本文采用有限元软件Ansys对结构进行动力时程分析，结构本身的质量简化成等效质量单元MASS21，阻尼系数采用瑞利阻尼算法。

1.2 动力失稳判别方法

运动稳定性一般指Lyapunov意义下的运动稳定性，有稳定、渐进稳定和不稳定3种。Lyapunov意义的动力稳定性，是研究初始条件的扰动对系统运动状态的影响。1892年，Lyapunov从理论上对运动稳定性的普遍问题作了严格论证和系统分析，提出了解决运动稳定性问题的两种方法。这种理论称为Lyapunov稳定性理论［3］。国内外学者已对结构动力稳定性问题做了大量研究，各自提出稳定性或不稳定性的定义和准则。目前主要有以下几种准则，基于Lyapunov运动稳定性理论的判别方法［4－7］，能量法［8，9］以及是 Budiansky-Roth运动准则，简称为B-R运动准则，各自有着不同的特点和局限性，综合考虑，Lyapunov运动稳定理论的判别方法和能量方法，对于随时间变化的荷载作用下的非线性、多自由度复杂结构的动力稳定，不能提供有效的稳定性判别准则［10］。因此，目前基于系统响应来判别系统动力稳定性的Budiansky-Roth运动准则是较为直观、有效的方法:如果在某一荷载下，荷载的微小增量导致结构响应的显著增长，则该荷载被认为是该结构的动力稳定临界荷载。对于稳定屈曲后路径，只要曲线的拐点足够明显，可把曲线的拐点作为动力屈曲的临界点。

1.3 临时支撑卸载引起的结构失效判别准则

弦支穹顶结构在卸载冲击荷载(包括人为卸载及临时支撑工作中突然失效等偶然因素引起的冲击)下，可能发生由于动力失稳而失去继续承受荷载或变形不再满足使用要求的破坏，即结构发生临时支撑卸载失效［11］;结构具体的失稳破坏模式即为失效模式，结构即将失效或已经发生的内力或变形的数值或趋势，即为对应失效模式的预警参数。

本文提出以B－R运动准则［10］为基础、适用于弦支穹顶结构临时支撑卸载、改进的动力失稳判别准则:

(1)当屈曲后路径稳定时，计算不同持时三角形冲击荷载下的结构动力响应，绘制各点位移响应曲线。如果在某一荷载下，结构有节点振动开始发散或不收敛，则该荷载被认为是该结构动力稳定的临界三角形冲击荷载，即动力不稳定区域的下限。

(2)如果屈曲后路径不稳定时，尽管冲击荷载强度已很大，结构时程曲线尚未出现明显发散或不收敛现象，则认为结构已经发生强度破坏，可绘制结构冲击荷载－结构最大位移曲线，将其拐点或不明显的拐点处所对应的荷载值定为结构的冲击破坏临界荷载。

本文采用ANSYS有限元软件对标准弦支穹顶结构临时支撑不同卸载速率对结构稳定性能的影响进行分析，并寻找不利速率条件下结构的预警参数，并采用实例对本文所提的方法、结论进行验证。

2 分析模型

2.1 标准弦支穹顶结构

由于临时支撑建立和卸载是在结构设计完成之后进行的施工过程模拟，因此在进行施工方面的分析之前必须存在一个已经满足设计要求的结构。本文采用的分析模型达到标准弦支穹顶结构的要求。这里所谓的标准弦支穹顶结构是指在选定荷载的作用下各类构件的应力比小于并接近于设计强度、缺陷结构双重非线性稳定分析得出的临界稳定系数及结构的挠度满足要求的标准弦支穹顶结构。进行结构设计时需要做以下三个基本假设:

① 结构的边界条件为周边切向和竖向支承，径向自由，单层网壳采用梁单元，撑杆采用杆单元，索采用只拉不压的杆单元;

② 各环预应力拉索比值固定，比值是根据如下公式求解［12］:

式中:Fj为第j道环索上方单层网壳等效节点荷载;Nhcj为第j道环向索的轴向力;αj为第j道环索相邻索段的夹角;βj为第j道环索位置处相邻径向索在水平面上投影的夹角;γj为第j道环索位置处径向索与竖向撑杆的夹角。

③ 按照弹塑性方法进行几何非线性静力分析。

本文结构设计采用ANSYS有限元程序，上弦单层网壳杆件采用BEAM4单元模拟，撑杆采用LINK8单元模拟，索及拉杆采用LINK10单元模拟，材料本构关系为理想弹塑性，对结构进行非线性静力计算。根据各种荷载组合作用下的静力计算结果，对结构构件强度、稳定进行验算，只有满足规范要求的标准结构才能用来进行本文的施工分析。

④ 按照《网壳钢结构设计规程》(JGJ 61—2003)对弦支穹顶结构进行考虑材料弹塑性、初始几何缺陷的双重非线性稳定分析，得出的稳定临界荷载需满足要求。

2.2 数值模型和参数选取

为了考察直接卸载方式和慢速卸载方式对弦支穹顶结构的影响，本文选择突然卸载(卸载时间很短)、直接卸载方式(卸载时间较短)及慢速卸载(拟静力卸载)三种卸载方式进行比较，考虑到临时支撑可能会出现突然失效等偶然因素并且卸载速度有时难以掌握，根据工程经验分别选取了 tr=0.01 s、0.05 s、0.50 s、1.00 s和2.00 s卸载荷载作用时间进行分析。表1给出了具体工况以及对应的卸载荷载作用时间。

表1 卸载荷载作用时间Tab.1 Acting time for the impact load

本文计算模型为跨度为90 m、矢高为15 m、垂跨比为0.466的标准弦支穹顶结构。单层网壳的周边环杆截面采用φ300×10钢管，第5环单层网壳环杆截面采用φ250×10钢管，其他单层网壳杆件采用φ203×10钢管;撑杆采用φ125×6钢管;6道径向索和6道环向索均采用钢绞线7×4。钢管和索的弹性模量E1、E2分别为 2.1E+8 kN/m2、1.8E+8 kN/m2。

根据预应力设计原则［2］，本文编制了可以计算各环预应力比值的程序PREPM，计算出该结构形式的8环预应力比值为(由外而内):1423∶1209∶1036∶438∶317∶228∶57∶1。由比值可知，内两道环索预应力比值很小，在该位置设置拉索对结构贡献不大，反而容易松弛，施工中也不易控制，因此，内两环不设置拉索。第1道 R 第6道环索预应力设计值比值为 6.3∶5.31∶4.56∶1.92∶1.39∶1.00 ，其中最外环环索预拉力设计值为200 kN。满布的临时支撑截面为φ250×10(数值模型中简化为1 m长标准支撑)。对结构进行缺陷双重非线性稳定分析，得到的结构临界稳定系数和最大组合应力比(包括强度和稳定)均符合标准结构的定义，可作为本文的数值计算模型使用。

用ANSYS程序对结构进行动力响应时程分析时，节点自重按总重的25%折算成质量块施加到单层网壳节点上，支座节点上的质量块质量为126 kg，单层网壳其它节点上的质量块质量为151 kg。由考虑预应力效应的动力模态分析算得第1阶振型频率为3.341 Hz，由此频率计算出 α =0.8397、β =0.0019。

该弦支穹顶结构采用各环同步张拉施工方法，且一次张拉到位。张拉全过程分析完毕时，只有最外环临时支撑尚未脱离主结构，其支承力均为28 kN。可将z向28 kN支承力作用在外环支承点处，代替尚未脱离主结构的最外环临时支撑的作用，然后对该已无临时支撑支承的结构进行卸载模拟分析，其中，卸载模拟分析方法可根据卸载时间的长短确定采用瞬态分析方法或拟静力分析方法，具体见表1。将临时支撑z向的支承力作用称为卸载荷载。

3 卸载速率对结构的影响分析

3.1 tr=0.01 s作用时间下对结构性能的影响

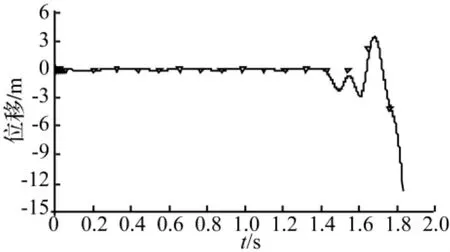
图1 位移时程曲线Fig.1 Time-history displacement curve

将z方向的28kN卸载荷载作用于相应各支承点处，作用时间为0.01 s，对结构进行瞬态分析。图1给出了此种作用荷载下96节点的时程响应曲线。由该曲线可知，节点在1.43 s之后出现运动发散，结构在该点处已局部失稳;从图2弦支穹顶整体弹塑性变形图(a)可知，此时内环索编号为644、645两节点严重偏离初始位置，已局部失稳。

表2给出了tr=0.01 s卸载荷载作用时间下结构的弹塑性响应。从该表可以看出，tr=0.01 s作用时间下，结构最大应力比值已达到100%承载能力。

图2 弦支穹顶整体弹塑性变形图Fig.2 Elastic-plaxtic comfiguration of the structure

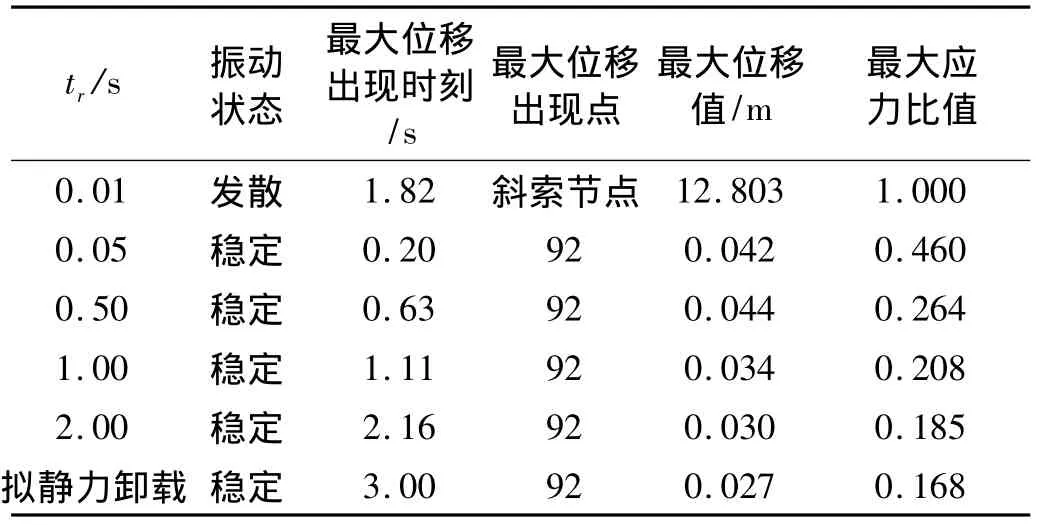
表2 结构在卸载荷载作用下的弹塑性响应Tab.2 Elastic-plastic response of the structure under unloading impact

3.2 不同卸载方式对结构性能的影响

图3给出了卸载荷载作用时间tr分别为0.05 s、0.5 s以及2 s下节点96的位移时程曲线。由图可知，在 0.05 s、0.5 s、2 s作用时间下节点只有振幅的不同，随着作用时间的减小振动振幅加大，但振动不发散。从图2所示的弦支穹顶弹塑性整体变形同样可看出这种特性:随着作用时间减小，临时支撑位置处的上部节点振动加大。表2给出了结构在 0.05 s、0.5 s、2 s卸载荷载作用下的弹塑性响应值。由该表可知在0.05 s、0.5 s、2 s卸载荷载中，0.05 s卸载荷载作用下结构的应力比和位移最大，随着作用时间的增加，卸载荷载对结构的影响依次减小，越来越接近拟静力下的响应值。

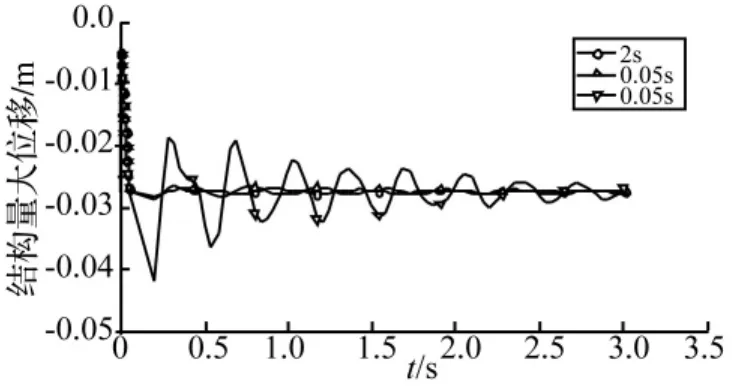
图3 位移时程曲线Fig.3 Time-history displacement curve

由以上分析可知，卸载时间对结构动力响应的影响很大:时间tr越长，动应力和动位移越小，对结构性能的影响越小;时间tr越短，动内力和动位移越大，对结构性能的影响越大;卸载时间短到一个临界时间trcr将会导致结构局部失稳，进而引起结构整体失效。因此，可将临界卸载时间trcr定义为结构临时支撑卸载拆除的结构失效预警参数。本算例的临界卸载时间trcr为0.01 s。

虽然在tr=0.5 s到 2 s卸载荷载作用时间内(＞trcr)，结构动位移和动力均没有超出设计值，但均大于其静力响应值，并且实际结构由于制作、安装误差等存在各种缺陷，有缺陷结构在动荷载下往往更不利，进一步说明，如果采用直接卸载，操作上是很难掌握具体的临界卸载时间trcr，一旦超过安全的临界卸载时间trcr，则存在一定的危险。因此从以上角度考虑，对结构进行分阶段慢速，即卸载时间卸载tr＞trcr，是一种合理、安全的卸载方式。

实际上，临时支撑拆除的临界时间trcr与临时支撑的反力密切相关，反力越大，trcr越大，因此，对于大跨度的结构临时支撑拆除时间控制尤为重要。

3.3 卸载失效模式和预警

从上述算例分析可知，临时支撑卸载不当或过快(tr≤trcr)可能引起结构失效。结构卸载失效模式为局部失稳引起的整体失稳，失稳点为拆除支撑处对应的网壳节点。支承处网壳节点振动发散为结构卸载失效的具体模式。因此，对弦支穹顶结构临时支撑拆除过程的卸载失效预警参数为卸载临界时间trcr和支承处网壳节点的振幅，即通过确定临界卸载时间trcr和观察该点的振动效应，可对临时支撑拆除过程进行预警，防止结构失稳。

4 实际工程临时支撑卸载分析

4.1 2008年奥运会羽毛球馆卸载失效模式分析

在2008年奥运会羽毛球馆实际施工(如图4施工中的奥运会羽毛球馆内景所示)中，当环索张拉力达到70%的预张力时，将其未脱离的支撑直接卸载。鉴于直接卸载的风险性，本文对其直接卸载的结构安全性进行分析，根据工程经验选择卸载时间tr，如表3所示。

图4 施工中的奥运会羽毛球馆Fig.4 The badminton gymnasium for 2008 Olympic Games under construction

首先对结构在70%预应力设计值下的各临时支撑支承力进行双重非线性静力分析，图5给出了结构的有限元模型和部分节点编号。其中，索撑节点采用在ANSYS软件平台上进行二次开发的可滑移节点［11］:撑杆下节点、径向索单元节点共用一个节点，而环索采用单独节点，在环索节点竖向和法向与径向索单元节点进行耦合，并在二者之间建立切向弹簧单元，依此模拟环索和撑杆下节点的径向滑移并可在滑移方向上形成一定的滑移刚度。计算结果发现，只有最外两环临时支撑尚未脱离，其支承力分布在34 kn～28 kn之间。将相应支承力反向加在结构次外环支承点处，以取代临时支撑的作用，并对结构按照本文所提卸载方法进行分析。

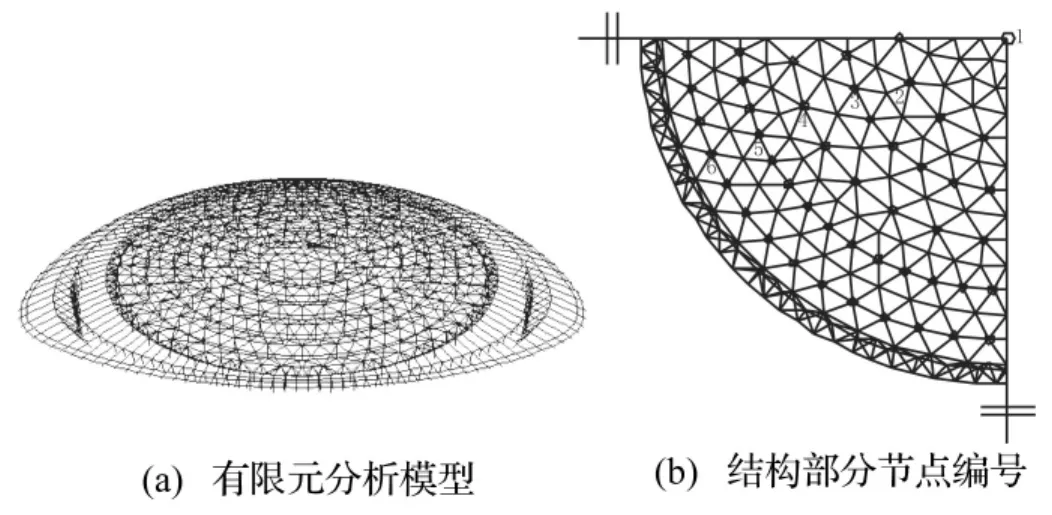
图5 羽毛球馆有限元分析模型Fig.5 Numerical model of the suspen-dome

图 6 给出了 tr=0.008 s，0.01 s，0.1 s及 1 s卸载时间下结构节点5的位移时程曲线。从图中可知，随着卸载的加快，该节点的振动幅度加大。根据计算，当卸载时间减到0.004 s时该点率先首次出现发散，如图7所示，短短0.8 s内，该点的振动已达0.6 m;根据动力失稳判别准则，该点已经局部失稳，最终导致整体失稳。

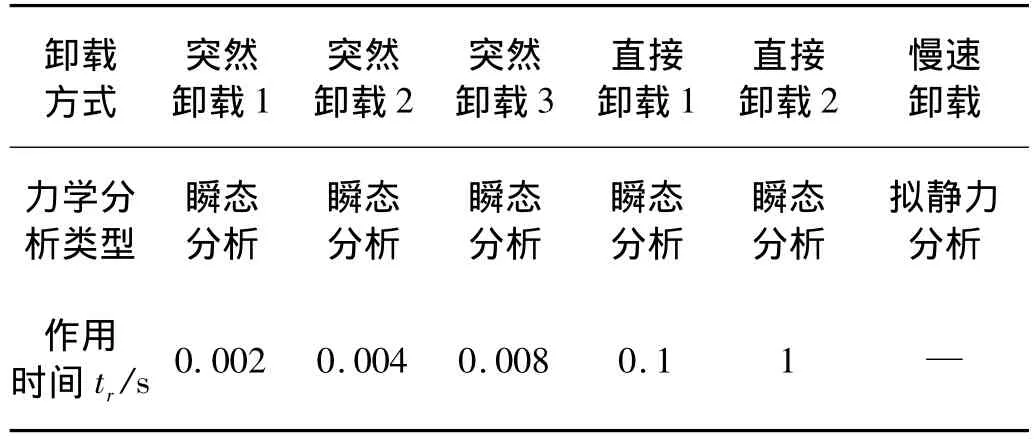
表3 卸载荷载作用时间Tab.3 Acting time for the impact load

图6 节点5位移时程曲线Fig.6 Time-history displacement curves of Node 5

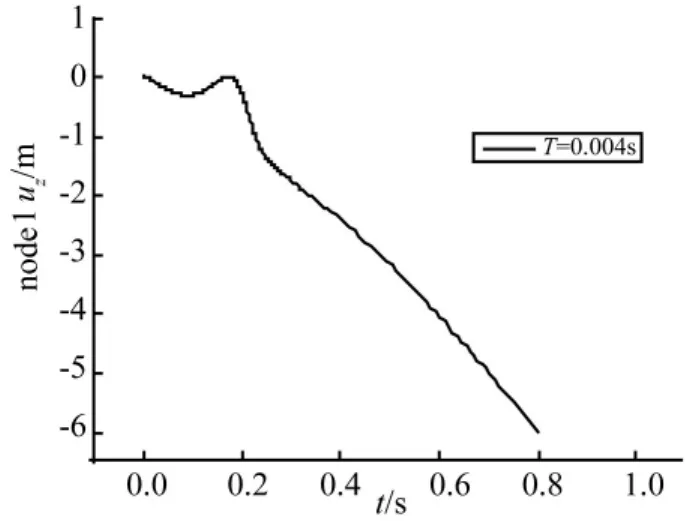
图7 节点5位移时程曲线Fig.7 Time-history displacement curves of Node 7

根据本文失效准则和失效判断方法，结构的临界卸载速率tcr可定为0.004 s，失效模式为局部失稳导致的整体失稳，预警参数上限可取tcr的值。

4.2 2008年奥运会羽毛球馆卸载失效机理研究

图8(a)～图8(d)给出了结构在tr=0.004 s，即tcr下索撑节点的滑移状况和上部网壳变形。从图8(a)，图8(b)可知，索撑节点在0.1904 s开始滑移，并在以后的振动中滑移幅度不断加大，与此同时，上部网壳局部变形开始加大，在索撑节点滑移的部位，局部杆件出现屈曲，如图8(c)、图8(d)所示;对照图5发现，节点2在稍后开始振动发散。

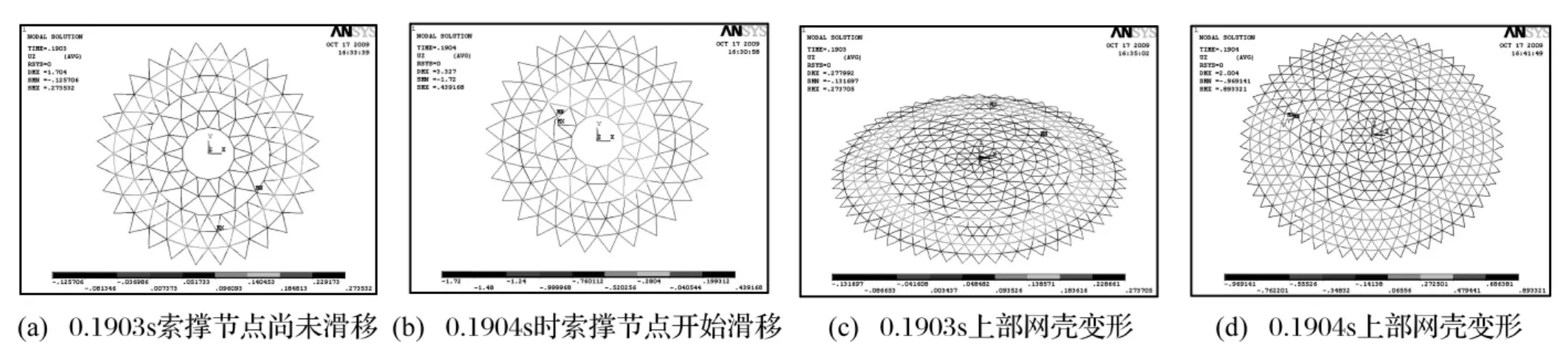
图8 tr=0.004 s结构变形Fig.8 Configuration of the structure for tr=0.004 s

从弦支穹顶结构的张拉受力机理角度分析，通过对索施加预应力，上部单层网壳将产生与荷载作用反向的变形和内力，从而使结构在荷载作用下上部网壳结构各构件的相对变形小于相应的单层网壳，使其具有更大的安全储备;而竖向撑杆对于单层网壳起到了弹性支撑的作用，可以减小单层网壳杆件的内力，调整体系的内力分布，降低内力幅值，从拉索强化单层网壳的角度出发，拉索部分不仅增强了总体结构的刚度，还大大提高了单层网壳部分的稳定性。从图8(b)可知，索杆节点在冲击荷载下沿环索滑移，导致撑杆竖向倾斜角度很大，此处上部网壳结构的“弹性支撑”作用减弱，在冲击荷载下迅速失稳，局部的网壳失稳最终导致了整体结构的失稳。因此，卸载过程中索撑节点沿环索的滑移可作为结构失效的预警参数下限。

在实际施工中，卸载支撑时，可以将索撑节点暂时固定，或者将索撑节点的可滑移范围通过一些措施限制在一定长度内，防止索撑节点过度滑移造成的竖向撑杆过度倾斜，增强结构安全性。

5 结论

本文提出了适用于弦支穹顶结构临时支撑卸载、改进的动力失稳判别准则，利用该准则和有限元分析，选择直接卸载、突然卸载、慢速卸载三种卸载方式对弦支穹顶结构施工中临时支撑拆除卸载进行模拟分析，计算结果表明:(1)采用直接卸载方式操作上很难掌握具体的卸载时间，尤其是临界卸载时间trcr，如果一旦卸载过快，则存在一定的安全风险，而分阶段慢速卸载(tr＞trcr)是一种较为合理、安全的卸载方式;(2)临时支撑卸载不当，可能起结构失效，失效模式为局部失稳，预警参数为临界卸载时间trcr和支承处网壳节点振动，失效特征为支承处网壳节点出现较大幅度的振动甚至发散，可供结构方案设计和施工调整参考。(3)2008年奥运会羽毛球馆的临时支撑卸载失效分析验证了本文所提临时支撑卸载失效判别准则和结论的正确性和可行性，且其机理分析表明，卸载时固定索撑节点或减少其沿环索的滑移范围，可达到加强卸载安全性的目的。

［1］Robert G S.Reliability during Temporary Erection Phases［J］.Engineering Structures，1998，20:999 －1003.

［2］刘 涛.大跨度空间结构施工的数值模拟与健康监测［D］.天津:天津大学，2005.

［3］沈 平.过程控制理论基础［M］.杭州:浙江大学出版社，1997:282－300.

［4］郭海山，沈士钊.单层网壳结构动力稳定性分析［J］.建筑结构学报，2003，24(3):1－9.

［5］王 策，沈士钊.单层球面网壳动力稳定性［J］.土木工程学报，2001，33(6):17 －24.

［6］Goldhirsch I，Sulem P L，Orszag S A.Stability and Lyapunov stability of dynamical systems:A diferential ap-proach and a numerical method［J］.Physica，1987，27(3):11 －337.

［7］沈祖炎，叶继红.运动稳定性理论在结构动力分析中的应用［J］.工程力学，1997，14(3):21－28.

［8］Simitses G J.Suddenly-loaded structural configuration［J］.J EngMech Asce，1984，l10(9):1320 －1334.

［9］Simitses G J.Effect of static preloading on the dynamic stability of structure［J］.AIAAJ，1983，21(8):117 －118.

［10］罗永峰，刘慧娟，韩庆华.弦支穹顶结构动力稳定性分析方法［J］.西南交通大学学报，2008，43(6):729 －735.

［11］刘慧娟.弦支穹顶结构施工过程模拟分析研究［D］.上海:同济大学，2009.

［12］郭 云.弦支穹顶结构形态分析、动力性能及静动力试验研究［D］.天津:天津大学，2003.