直斜裂纹转轴的时变刚度特性研究

刘长利，李 诚，周邵萍，夏春明

(1.华东理工大学 机械与动力工程学院 承压系统安全科学教育部重点实验室，上海 200237;2.上海交通大学 机械系统与振动国家重点实验室，上海 200240)

大型旋转机械转轴上的疲劳裂纹是工业机组的重大隐患。含裂纹转子的非线性动力学特性主要是转轴的局部时变刚度造成的。使用开关函数描述裂纹的呼吸效应主要有方波模型，余弦波模型和高－朱模型等。李允公等［1］指出开关函数具有相位调制特点，开关函数与时变刚度间有幅值调制特点。Dimarogonas等人［2］提出了著名的采用断裂力学理论来计算裂纹轴的附加柔度。Papadopoulos等［3］利用截断的余弦级数模拟裂纹转轴在旋转过程中裂纹轴段的刚度变化。Darpe等［4］提出应力强度因子为零法模拟裂纹的呼吸效应，即当第一应力强度因子大于零时裂纹的尖端场为拉应力，裂纹处于张开状态。文献［5］提出中性轴法模拟裂纹的呼吸效应，即寻找两主方向不同力的比值作用下裂纹截面的中性轴，作为拉压区域的分界线。前者得到的刚度曲线光滑且与试验曲线的近似程度大，是比较好的刚度理论模型。Darpe等分析了含直裂纹［4］和斜裂纹［6］的转子的动力学特性，但是没有详细研究转子在旋转时，裂纹引起的刚度时变规律。何为等［7］推导了含横向裂纹转轴的刚度矩阵，分析了裂纹深度比和转轴细长比等参数对转轴刚度的影响，但是裂纹转子的刚度变化规律在静止状态下和旋转状态下还是有较大区别的。

本文采用Dimarogonas等提出的应变能释放率方法推导了裂纹单元的刚度矩阵，采用Darpe提出的应力强度因子为零法模拟裂纹的呼吸效应，详细研究了不同深度的直裂纹和45°斜裂纹转子，在一个稳态旋转周期内，裂纹开闭规律以及转轴刚度时变特性。

1 裂纹单元刚度矩阵及系统动力学方程

1.1 裂纹单元的刚度矩阵

考虑梁的转动惯量和剪切变形，在静止坐标系下Jeffcott转子系统的横向振动方程为:

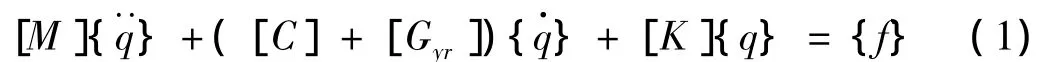
式中:［M］、［C］、［Gyr］、［K］分别是转子的总体质量矩阵、阻尼矩阵、陀螺矩阵和刚度矩阵。别为节点上的加速度、速度和位移矢量。{f}为外激振力，包含重力和不平衡力。

含裂纹转子轴段如图1所示。轴段受到轴向力P1，P7，剪力 P2，P3，P8，P9，扭矩 P4，P10，及弯矩 P5，P6，P11，P12等力的作用。

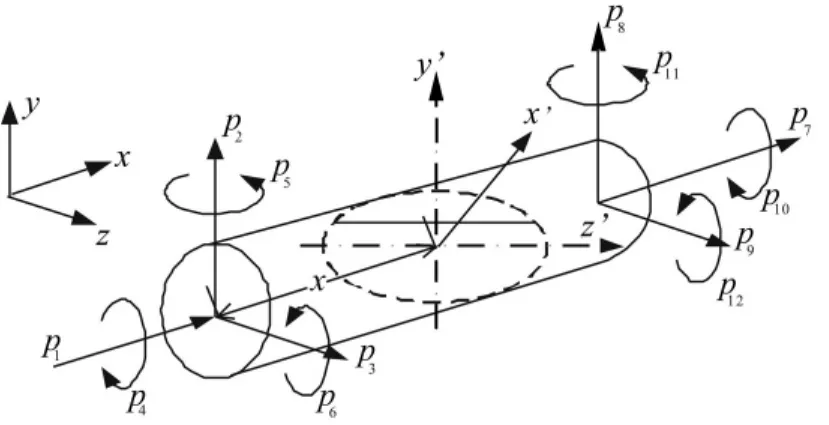
图1 裂纹单元的力学模型Fig.1 The mechanical model of the cracked element

转子无裂纹轴段的应变能如式(2)所示:

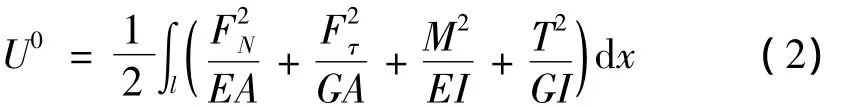
由图1中转子裂纹单元的受力情况可知，转子的应变能为:

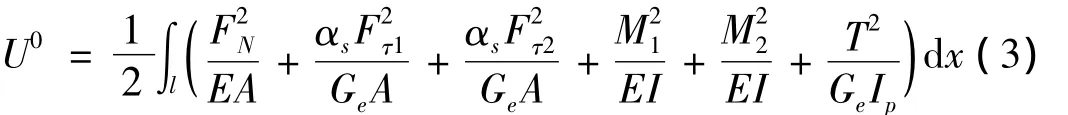
其中，T 为扭矩，FN为轴向力，Fτ1，Fτ2为剪力，M1，M2为弯矩，E为材料的弹性模量，Ge为切变模量，I为转轴的惯性矩，Ip为极惯性矩，A为圆截面面积，αs为剪切系数。如图 1 所示，则 T=P4，FN=P，Fτ1=P2，Fτ2=P3，M1=P3x+P5，M2=P2x－P6。故无裂纹轴段的柔度系数为:

根据断裂力学理论，由裂纹扩展引起的附加应变能为［2］:

其中G(A)为应变能密度函数，其表达式为:

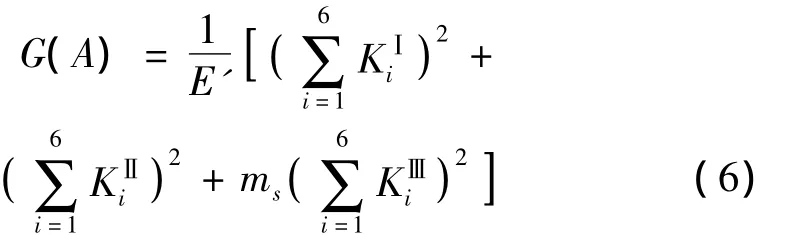
其中 E '=E/(1 －v2)，ms=1+v、、(i=1－6)分别为Ⅰ型、Ⅱ型、Ⅲ型裂纹的应力强度因子，则附加柔度系数为:

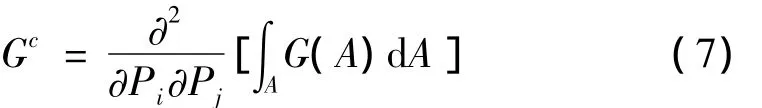
由式(4)和式(7)，得到裂纹单元整体柔度系数为:

故裂纹轴段的单元刚度矩阵可表述为:

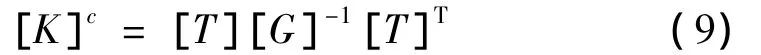
其中转换矩阵［T］如下式，其中l为单元的长度。

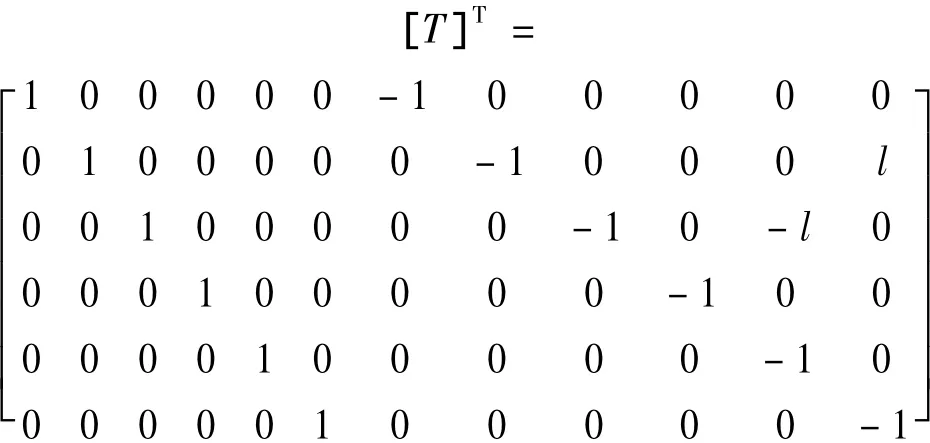
1.2 转轴裂纹的呼吸效应

确定裂纹单元柔度矩阵中各柔度项，即式(7)的积分区域A。根据断裂力学的概念，对于Ⅰ型裂纹，裂纹截面上应力强度因子的KⅠ的值为正，表示该处受拉应力，裂纹张开;反之受压应力，裂纹闭合。张开型裂纹的6个应力强度因子分量为［6］:

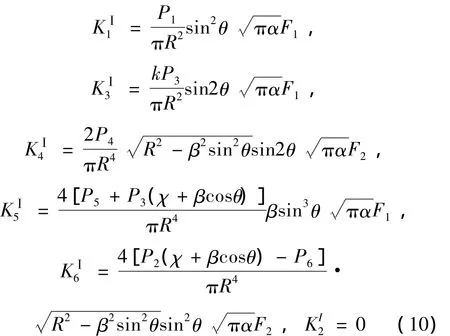
其中θ为裂纹截面与转子轴线的夹角。

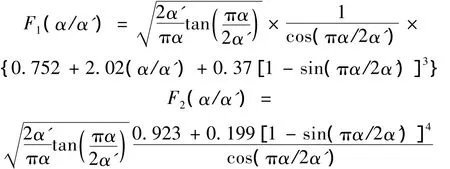
P1～P6是在固定在转子上的旋转坐标系作用于裂纹单元上的节点力，如图2所示。χ是裂纹中心距单元左端的距离;β为裂纹边缘与裂纹中心线间的距离;α为裂纹边缘的裂纹深度;α'为增量dβ的总高度;θ为斜裂纹的偏角;对于圆截面，形状系数k=6(1+ν)/(7+6ν)，ν为材料的泊松比。

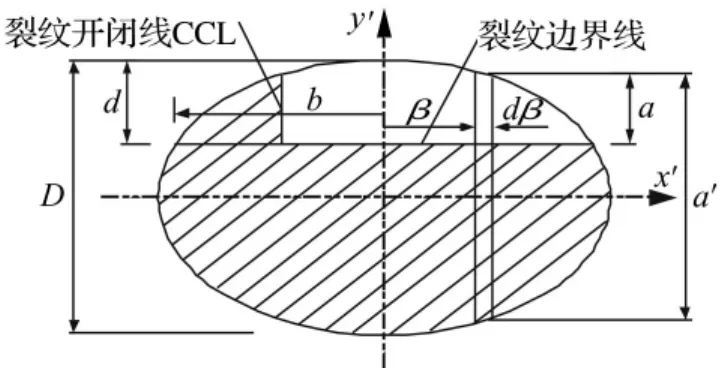
图2 裂纹截面示意图Fig.2 Crack cross section

张开型裂纹的截面某点处的应力强度因子和为:

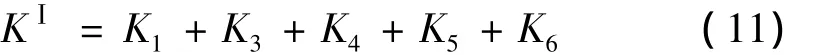
KⅠ的正负即表示该处的受力状态与裂纹的开闭。

将裂纹边平均分成50份，采用式(11)，沿裂纹边缘线依次计算各点的总应力强度因子，在KⅠ变号的位置作垂线垂直于裂纹边界线，该垂线即为裂纹开闭线(CCLP)［4］，如图3所示。开闭线一侧区域(包括裂纹边界线)的点受拉应力张开，另一侧的点受压应力而闭合。确定了转轴某一转角下裂纹截面的开闭区域，就确定了裂纹单元各柔度项的积分区域，即可得到该转角下对应的裂纹单元刚度。

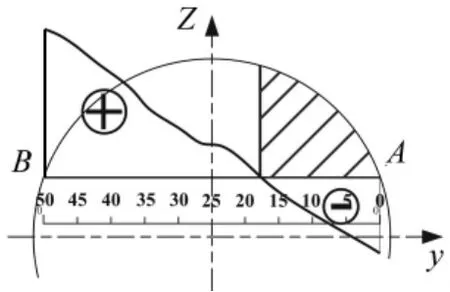
图3 裂纹开闭线位置的变化点分布图Fig.3 The position of crack closure line

2 裂纹截面的开闭变化研究

本文采用Timoshenko梁单元对Jeffcott转子建模，每个节点具有6个自由度。转轴共划分为14个单元，圆盘位于转轴中央，裂纹紧邻圆盘。转轴长度为560 mm，半径为10 mm。圆盘的半径为37 mm，宽度为25 mm，偏心e=1.65×10－5m。转轴和圆盘的弹性模量E=2.11 ×1011Pa，泊松比 v=0.3。

计算得到的无裂纹转子的前二阶横向固有频率为36.02 Hz和161.44 Hz。根据系统的前二阶固有频率得到质量阻尼Alpha=1.1019，刚度阻尼Belta=2.382×10－4。转轴的旋转速度为18 Hz。采用Newmark法计算转子的响应，积分参数取 α=0.2525，δ=0.505，采样频率为f=1024 Hz。

本文以无裂纹转子的静变形作为初始条件，转子的初始刚度矩阵为无裂纹转子的刚度，此时裂纹在重力作用下处于全闭的状态。转子在每一个旋转角度下，根据应力强度因子为零法确定裂纹的开闭位置，进而得到裂纹单元的刚度矩阵，用其来更新转子的总体刚度矩阵，再计算下一旋转角度下转子的响应，以求解对应的新裂纹开闭状态和裂纹单元的新刚度矩阵。由此得到呼吸裂纹的开闭规律和裂纹单元刚度变化特性。

2.1 直斜裂纹截面开闭变化分析

以直裂纹相对深度a=0.3为例，如图4所示，当转子转角由φ=0°转至φ=23°，裂纹截面仍处于闭合状态;当转子转过φ=23°，截面开始由A端张开;转至φ=157°，裂纹完全张开;转子转过φ=203°时，裂纹截面再次由A端开始逐渐闭合;在φ=337°达到完全闭合，至φ=360°完成一周期的变化。

图5为斜裂纹相对深度a=0.3时裂纹截面的开闭变化。与图4所示的直裂纹的呼吸过程相比，斜裂纹开始张开和闭合的时间较直裂纹有所延迟，当裂纹处于半开半闭时，延迟达到了10°的旋转角;直裂纹处于全闭与全开时的角度跨度都为46°，而斜裂纹为48°，其处于全闭与全开状态所经历的时间较对应的直裂纹略长。

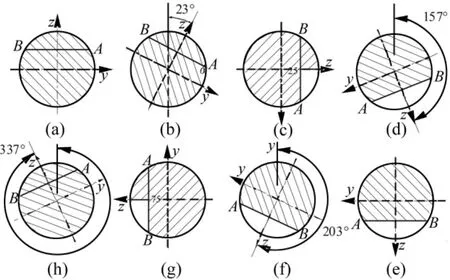
图4 相对深度0.3下直裂纹截面的开闭变化Fig.4 The opening/closing of transverse crack cross section when a=0.3

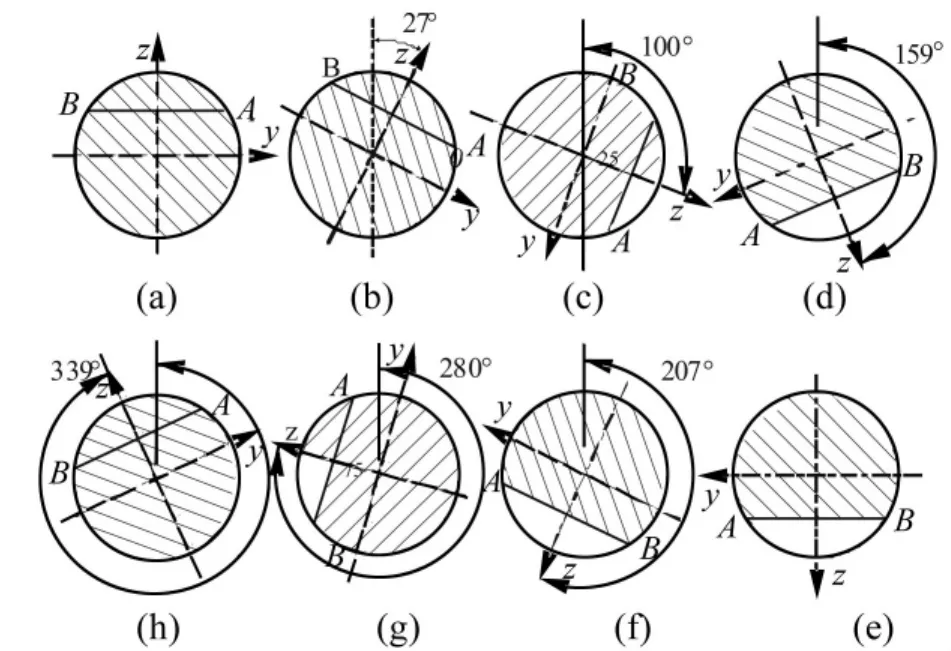
图5 相对深度a=0.3下斜裂纹截面的开闭变化Fig.5 The opening/closing of slant crack cross section when a=0.3

2.2 裂纹深度对裂纹截面开闭的影响

表1和表2分别给出了不同裂纹深度下，直裂纹和斜裂纹截面各个开闭状态对应的转角范围。由表可知，裂纹截面并非只在 φ=0°(360°)或 φ =180°时才处于全开或全闭状态，而是各对应一定的转角范围。随着裂纹深度的增大，裂纹全开、全闭状态的转角范围减小，由闭到开和由开到闭的转角范围增大，即开闭的过渡过程变得明显。同时，斜裂纹各状态的转角范围与直裂纹基本相同，但各状态的始末角位置都略微滞后。

表1 不同裂纹深度下关于表面直裂纹开闭的转子转角Tab.1 The opening/closing angle of transverse crack cross section with different crack depth

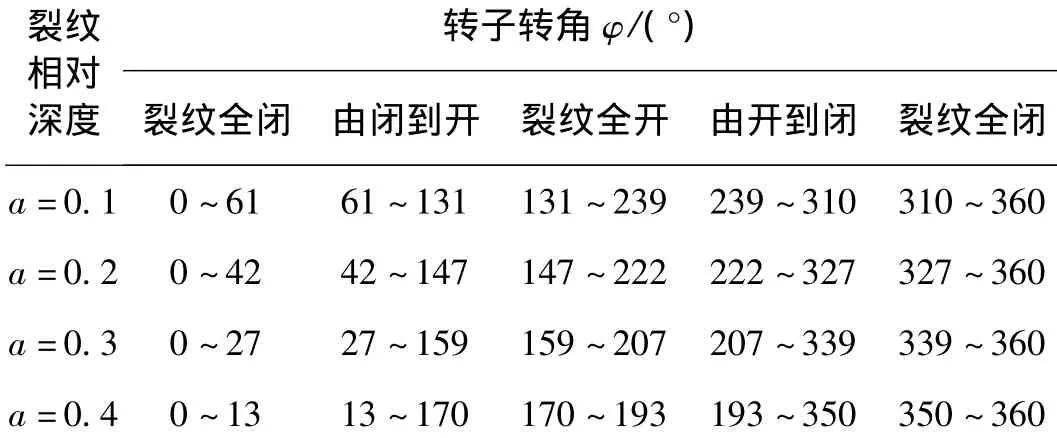
表2 不同裂纹深度下关于表面斜裂纹开闭的转子转角Tab.2 The opening/closing angle of slant crack cross section with different crack depth

3 裂纹转轴的刚度变化研究

利用Visual Fortran 6.5编制的有限元程序，改变裂纹的深度参数与裂纹截面与转轴轴线的夹角，分别得到直裂纹和斜裂纹转轴，稳定转动一周内各个转角的单元刚度矩阵，分析呼吸裂纹的刚度变化特性。

3.1 主刚度项的时变特性

图6给出了裂纹单元主刚度随旋转角度和裂纹深度的变化。为了便于比较，同一刚度项的纵坐标的取值范围是一致的。由图6可知，对于浅裂纹(裂纹相对深度a=0.1)，直斜裂纹主刚度随转轴转角的变化并不明显。随裂纹深度的逐渐加大，裂纹单元的主刚度不同程度的降低。在较深的裂纹深度下，斜裂纹的轴向刚度(K11)比直裂纹大。裂纹深度对斜裂纹剪切刚度(K22，K33)的影响比直裂纹单元明显。直斜裂纹的弯曲刚度(K55，K66)在相同的裂纹深度下变化范围基本相同，但是斜裂纹的刚度变化不再关于转角φ=180°对称，斜裂纹的最小刚度值出现在转角φ小于180°的范围内。直斜裂纹的扭转刚度(K44)则基本相同。

3.2 耦合刚度项的时变特性

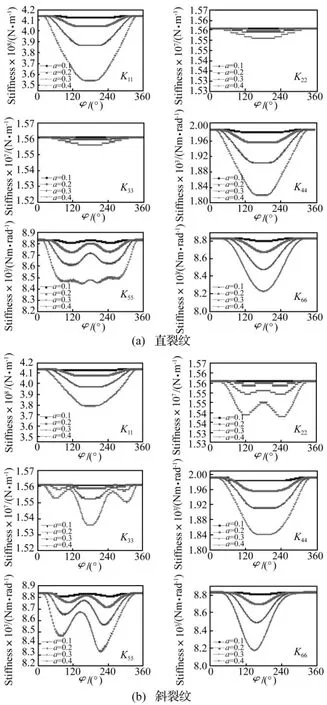
图6 裂纹单元主刚度随旋转角度和裂纹深度的变化Fig.6 Variation of direct stiffness coefficient with different crack depth and rotating angle

图7为裂纹单元耦合刚度随旋转角度和裂纹深度的变化图。耦合刚度项的存在是耦合振动产生的主要原因。直裂纹不存在弯曲与扭转振动之间的耦合(K45=0，K46=0)，以及轴向与扭转(K14=0)之间的耦合［如式(8)所示］。斜裂纹虽然存在弯曲与扭转振动之间的耦合，但是耦合作用也非常小。在所有的耦合刚度项中，除了K15和K16外，其余耦合刚度项的变化斜裂纹单元均大于直裂纹单元，表明直裂纹引起的转轴的轴向振动与横向振动的耦合作用较强，而其它几种振动之间，由斜裂纹引起的耦合作用强。直裂纹单元引起的轴向与剪切振动之间的耦合(K12，K13)，剪切与弯曲振动的耦合(K25，K36)非常小，与其他耦合作用相比可以忽略不计，而斜裂纹的此项耦合用作非常强。因此，斜裂纹与直裂纹相比较而言，引起了转子更多与更强的耦合振动，使转子的动力学性能更加复杂。综合图6、7，与文献［4］和［6］的结论相比，裂纹转子在一个稳态旋转周期内的转轴刚度时变特性与在静止状态下得到的规律有较大的差别。

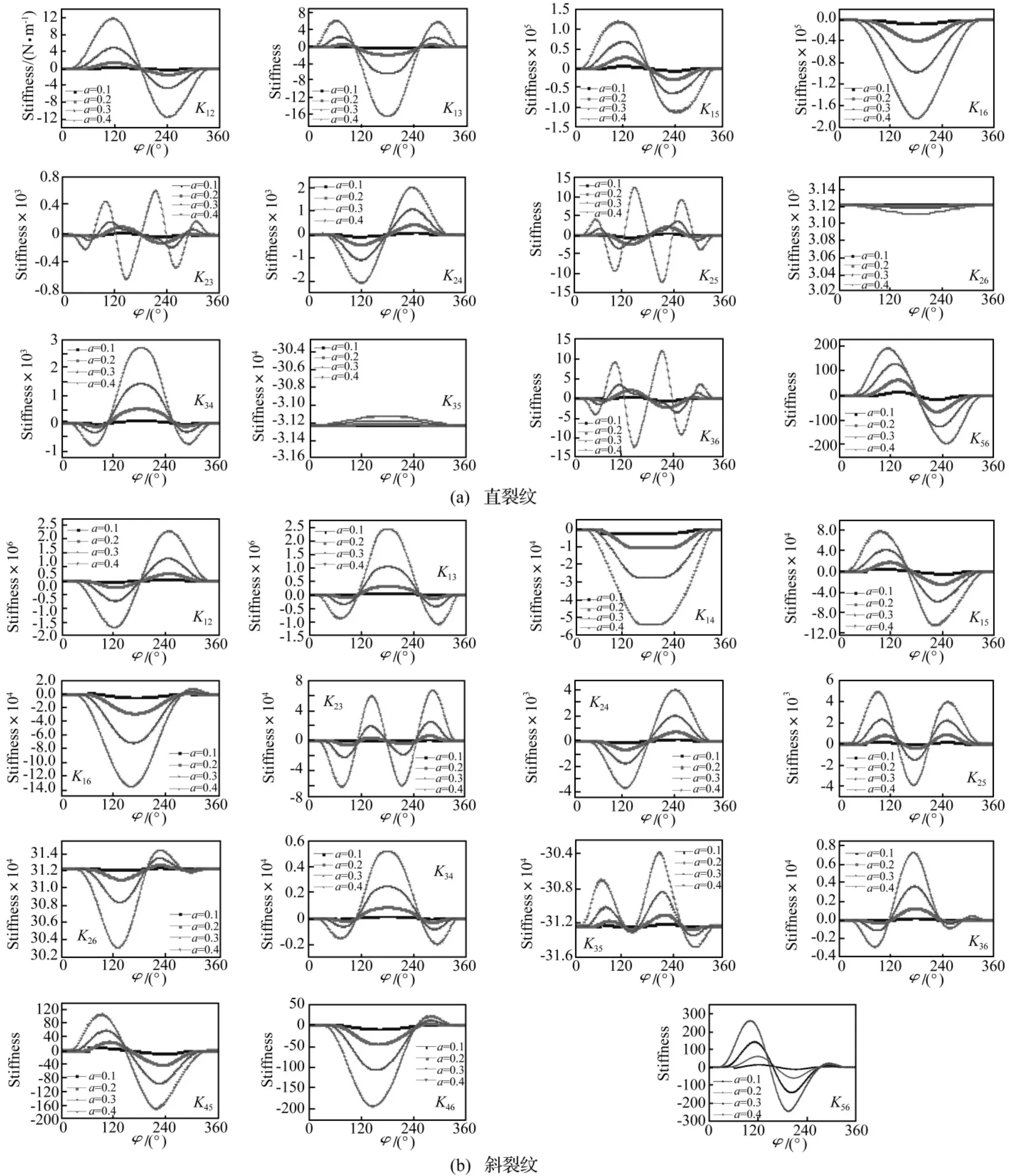
图7 裂纹单元耦合刚度随旋转角度和裂纹深度的变化Fig.7 Variation of coupling stiffness coefficient with different crack depth and rotating angle

4 结论

本文详细研究了不同深度的直裂纹和45°斜裂纹转子，在一个稳态旋转周期内，裂纹开闭规律以及转轴刚度时变特性。得到如下结论:

在转轴稳定运转时，裂纹截面的完全张开、完全闭合和过渡过程分别对应一定的转角范围。表面裂纹的深度越大，裂纹呼吸的过渡过程越明显。与直裂纹单元相比，斜裂纹单元的裂纹开闭变化转角相位滞后。

含直斜裂纹的单元在裂纹深度较浅时，主刚度随转角的变化不明显。随着裂纹深度增大，主刚度在一周变化中的减小量加大。同一裂纹深度下，直裂纹与斜裂纹单元各主刚度的变化特性存在差异。斜裂纹与直裂纹相比较，引起了转子更多与更强的耦合振动，使转子的动力学性能更加复杂。

［1］李允公，刘 杰，张金萍，等.呼吸裂纹故障动力特性及特征提取方法的研究［J］.振动与冲击，2004，23(3):37－41.

［2］Dimarogonas A D，Papadopoulos C A.Vibration of crackedshafts in bending［J］.Journal of Sound and Vibration，1983，91(4):583－593.

［3］Papadopoulos C A，Dimarogonas A D.Stability of cracked rotors in the coupled vibration mode［J］.Journal of Vibration A-coustics Stress and Reliability in Design，Transactions of the ASME，1988，110(3):356－359.

［4］Darpe A K，Gupta K，Chawla A.Coupled bending，longitudinal and torsional vibrations of a cracked rotor［J］.Journal of Sound and Vibration，2004，269(1－2):33－60.

［5］林言丽，褚福磊.裂纹转子的刚度模型［J］.机械工程学报，2008，44:114－120.

［6］Darpe A K.Coupled vibrations of a rotor with slant crack［J］.Journal of Sound and Vibration，2007，305:172 －193.

［7］何 为，任兴民，杨永锋.横向裂纹轴耦合刚度分析［J］.振动与冲击，2007，26(12):44－48.