惯性载荷对螺旋锥齿轮动态啮合特性的影响研究

唐进元，彭方进

(中南大学 现代复杂装备设计与极端制造教育部重点实验室;中南大学 机电工程学院，长沙 410083)

螺旋锥齿轮动态啮合问题是一个边界条件高度非线性的接触动力学问题，直接对其进行解析分析难度很大，有限元方法成为了计算螺旋锥齿轮问题的最普遍最有效的方法。

结构动力学分析中，惯性载荷一般是指由于结构的质量引起的动载荷。文献表明，国内外许多学者使用有限元方法对螺旋锥齿轮静态或者准静态接触特性进行了大量的研究［1－5］，但关于动态啮合特性的研究文献很少。而进行动态啮合有限元分析的必要前提之一就是建立准确的有限元模型［6］。已有文献中，螺旋锥齿轮的有限元模型可以概括为以下两种:一种是以Litvin等［4－6］为代表的刚体参考点耦合约束模型，即在轮齿轴线上建立刚体参考点，在参考点和小轮内圈和剖面间建立耦合刚体约束。由于分析时采用的是部分齿轮模型，这种方法无法表达真实齿轮的质量及其质心位置，从而不能体现真实惯性载荷的影响，不适合进行动态啮合分析;另一种则是李源等［7］采用的包含轮体的三齿啮合模型，一方面该模型的网格数量多，耗费了大量的机时，另一方面，该模型没有严格地反应真实的齿轮质量。

本文根据动力学原理和Lagrange乘子约束，提出了考虑惯性载荷的螺旋锥齿轮动态啮合分析有限元模型，应用到非线性接触动力学有限元分析中，并借助LS-DYNA软件对准双曲面齿轮的动态啮合特性进行了研究。

1 考虑惯性载荷的有限元模型

动力学问题的基本运动方程为:

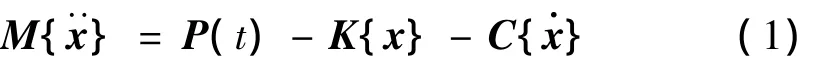
其中:M为质量矩阵，P(t)为载荷矢量，K为刚度矩阵，C为阻尼矩阵，为节点加速度矢量，为节点速度矢量，{x}为节点位移矢量。M即为惯性载荷。

在LS-DYNA3D程序中，运动方程描述为:

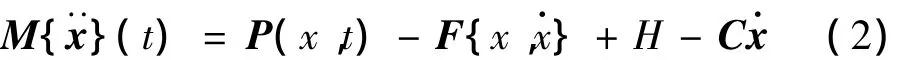
惯性载荷是使结构产生动力响应的本质因素，而惯性载荷的产生又是由结构的质量引起的。动态接触问题属于复杂的非线性动力学问题，必须考虑惯性载荷的影响。因此，对其结构的质量位置及其运动的准确描述成为了结构动力分析中的关键。

螺旋锥齿轮结构复杂，大轮和小轮的齿数相差大，如果对其进行完整一致的有限元网格划分，将极大增加计算规模，尤其对于动力学分析而言。

在有限元法中，应用Lagrange乘子约束可以实现将刚性体直接粘附在柔性体上［9］。一个简单的二维刚－柔性体问题如图1(a)所示，其中灰色为刚性体。图1(b)表示在刚－柔界面上的一个单元之间的分解图，这里需要强令单元的两个界面节点的位置具有与相应刚体上的点相同的变形位置。刚体的运动可以表示为:

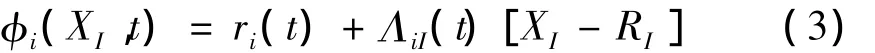
其中，XI是位置，t是时间，RI是在未变形物体中的某个参考点，ri是在变形物体中的同一个点的位置，ΛiI表示一个刚性转动。利用式(3)可以很容易写出这种约束:

式中脚标α代表节点数。应用经典Lagrange乘子法修改泛函使其包含该约束，经过处理可以得到每一个刚体的方程组为:

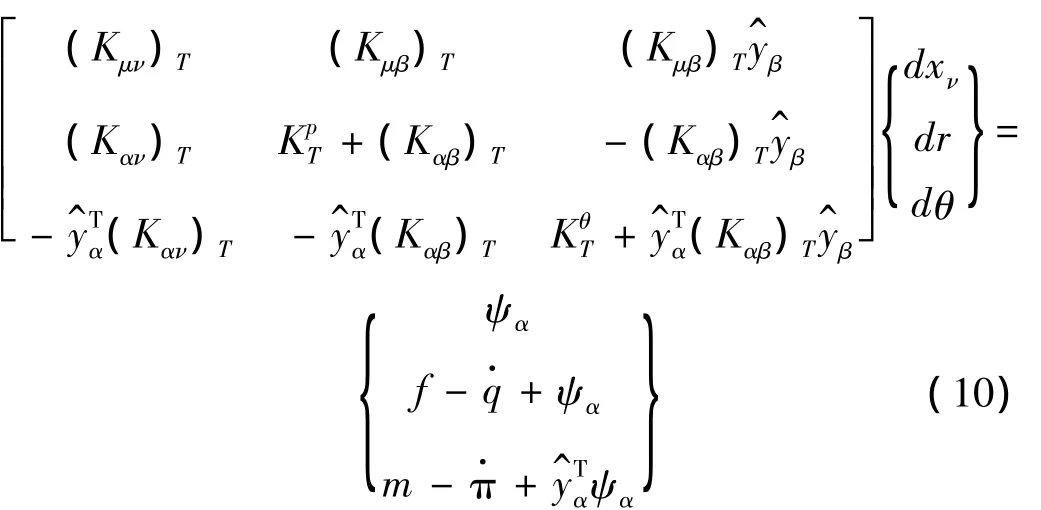
式中:ψα和ψμ分别是在节点α和 μ处有限元计算的残值，β是与节点α连接的任何其它刚体节点，μ和ν是与节点α连接的柔性节点，yα=xα－r是y的节点值。计算残值的步骤可以在每个单元中进行，于是，约束柔性体到刚性体的步骤仍是一个标准的有限元组装过程，而且很容易得并入到一个求解系统中。

综合考虑以上因素，针对螺旋锥齿轮动态啮合分析问题，本文提出一种新的有限元分析模型:建立大、小轮全齿模型，其中，对参与啮合的部分轮齿网格细分，不参与啮合的轮齿网格粗分，粗、细网格单元之间通过固连约束连接，这样既体现了真实模型的质量属性，又在满足分析精度的前提下尽量减小分析模型的单元规模。同时，应用Lagrange乘子约束，实现小轮与其内圈和大轮与其底面之间的刚柔约束，建立考虑惯性载荷的螺旋锥齿轮动态啮合分析边界加载模型，如图2所示。其中，图2(a)为完整的分析模型，图2(b)为分解模型，大锥形圆环为大轮底面，小锥形圆环为小轮内圈，大、小锥形圆环上的阴影曲面为固连约束的边界。

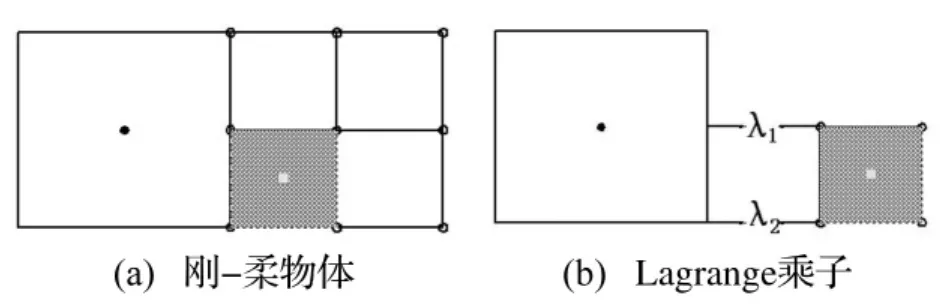
图1 刚性体和柔性体之间的Lagrange乘子约束Fig.1 Lagrange multiplier constrain between flexible and rigid bodies:(a)rigid-flexible body;(b)Lagrange multiplier

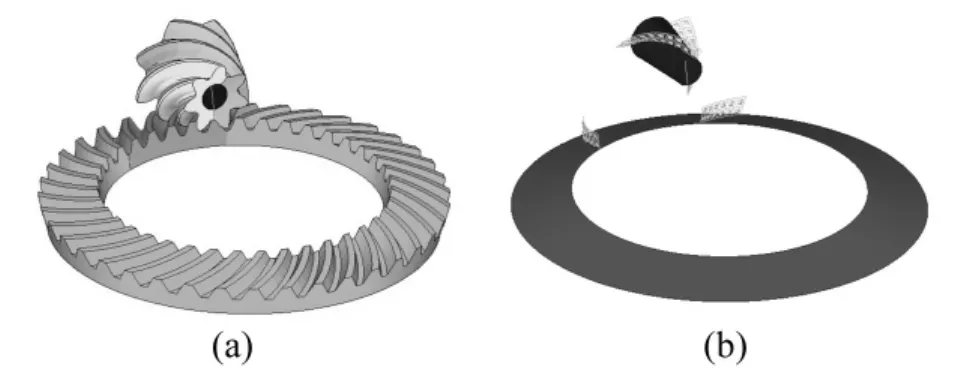
图2 准确的有限元模型Fig.2 Exact finite element model

2 准双曲面齿轮有限元模型建立

2.1 几何模型的构建

文章通过数值计算得到齿面离散数据点(主要几何参数见表1)，由离散数据点拟合成精确的准双曲面齿轮展成曲面，并依此构建出准双曲面齿轮三维实体模型，如图3所示。详细建模方法参照文献［10］，本文不再详述。

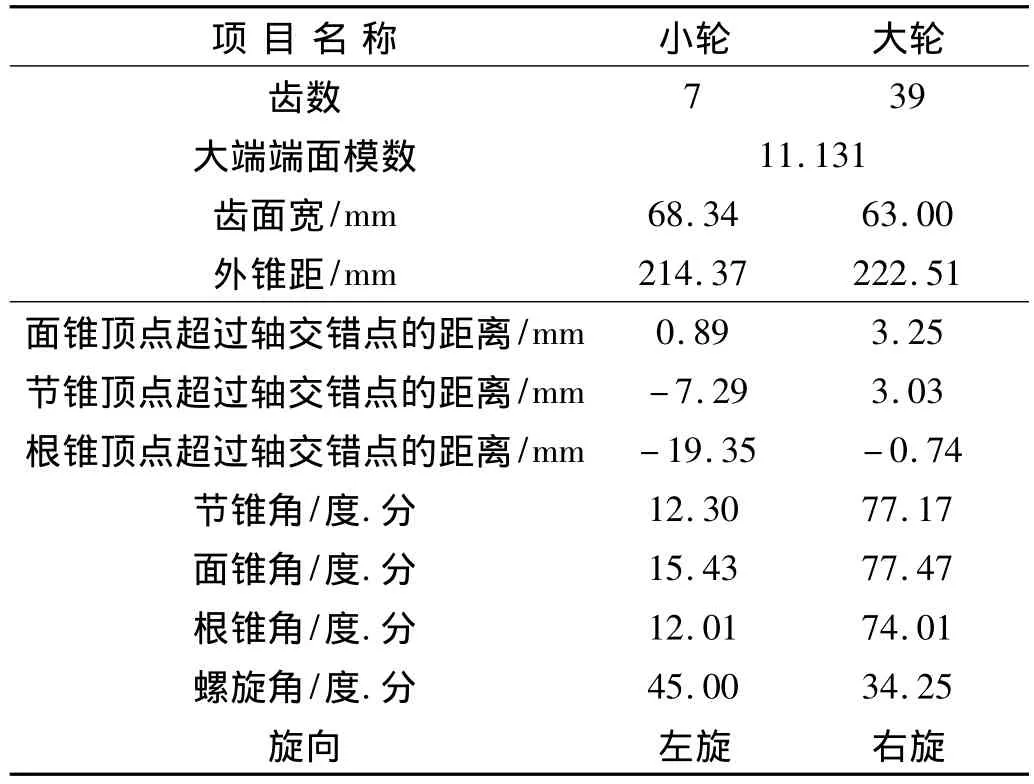
表1 准双曲面齿轮几何参数Tab.1 Geometric parameter of hypoid gear

图3 准双曲面齿轮几何模型Fig.3 Geometric model of hypoid gear

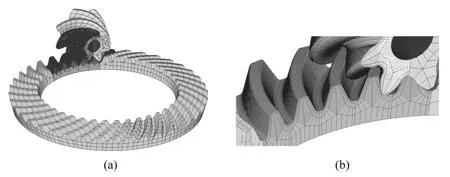
图4 准双曲面齿轮有限元网格模型Fig.4 Finite element model of hypoid gear

2.2 有限元网格划分

有限元网格划分是进行有限元数值分析至关重要的一步，它直接影响着后续数值计算分析结果的精确性。六面体网格由于其求解精度高、抗变形能力强、单元数量少等优点成为数值分析的首选网格。图4为准双曲面齿轮的六面体有限元网格模型，其中图4(b)为图4(a)的局部放大。

2.3 其他参数确定

大、小轮均采用弹性材料，弹性模量为2.1×1011Pa，泊松比为 0.3，密度为 7.8 × 103kg/m3，采用 solid164实体单元，单元积分形式为单点高斯积分，加上沙漏控制。大轮底面和小轮内圈采用刚体材料，弹性模量为2.1 ×1011Pa，泊松比为0.3，采用 shell163 壳单元，壳单元属性默认。

定义大轮和小轮之间为自动面面接触，约束大、小轮除了沿其各自轴线的旋转自由度以外的所有自由度，对小轮内圈施加恒定转速1200 r/min，同时对大轮底面施加恒定负载扭矩200 Nm。

3 计算结果与分析

基于上节所建立的有限元模型及确定的相关参数，应用LS－DYNA对螺旋锥齿轮的动态啮合特性进行有限元分析。

由于小轮转速及质量属性不变，可忽略其惯性载荷影响。因此，通过改变大轮的密度来改变大轮的质量属性，同时保持其他条件一致，以对比不同惯性载荷下准双曲面齿轮动态啮合的变化规律。分别建立三种对比模型，不同密度大轮与真实密度大轮的质量比分别为:0.1∶1，1∶1，10∶1，分别用代号Ⅰ、Ⅱ和Ⅲ表示。其中，模型Ⅱ为真实的齿轮模型。

3.1 惯性载荷对运动特性和齿面接触力的影响

为了避免强烈的初始啮合冲击，对小轮的转速采用逐步施加，如图5所示。

从大轮的转速变化(图6)可知，不同质量比模型的大轮转速均经过波动后近似于稳定值22.56 rad/s，但仍然呈现小幅波动，这与螺旋锥齿轮的传动特性是吻合的。随着惯性载荷的增大，大轮转速波动频率减小。

图5 模型Ⅱ的大小轮转速对比图Fig.5 Comparison diagram of the rotational speeds of gear and pinion in modelⅡ

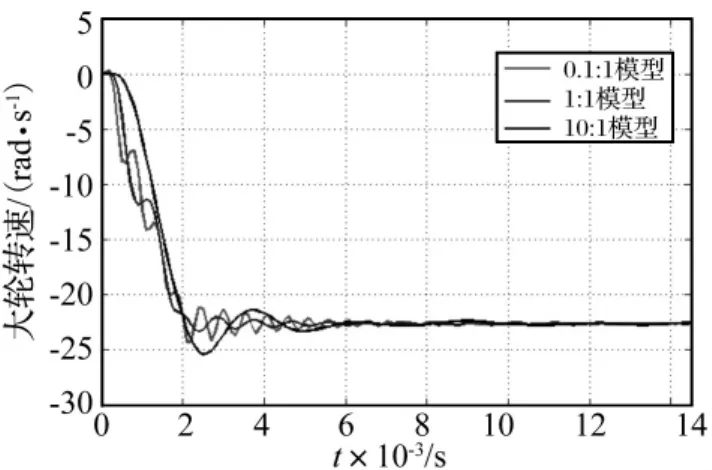
图6 不同质量比模型的大轮转速历程Fig.6 The gear’s rotational speed time history of different model

由图7、图8和图9可知，质量比为0.1∶1时，齿面最大接触力为18.98 kN;质量比为1∶1时，最大接触力为142.16 kN;质量比为10∶1时，轮齿最大冲击接触力为1194.20 kN。可见，随着惯性载荷的增大，齿面接触力波动幅值显著增大，波动频率明显减小。

综上，惯性载荷对螺旋锥齿轮运动特性、齿面接触力波动幅值和频率均有显著影响:随着惯性载荷的增大，大轮转速波动频率减小，齿面接触力波动的幅值增大，波动频率减小。

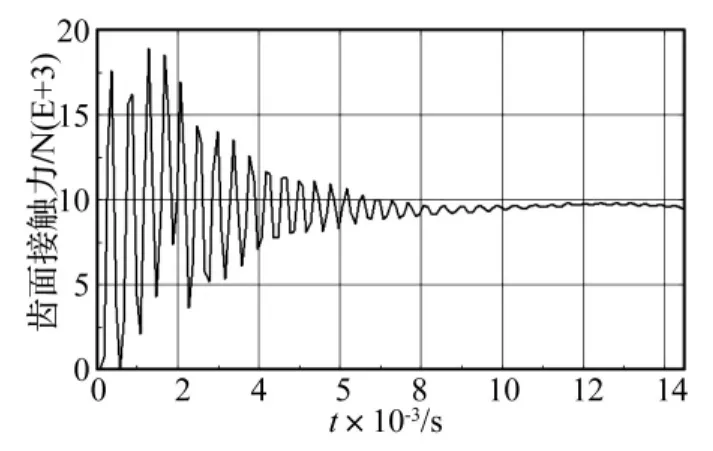
图7 模型Ⅰ的齿面接触力历程Fig.7 The tooth contact force time history of modelⅠ

图8 模型Ⅱ的齿面接触力历程Fig.8 The tooth contact force time history of modelⅡ

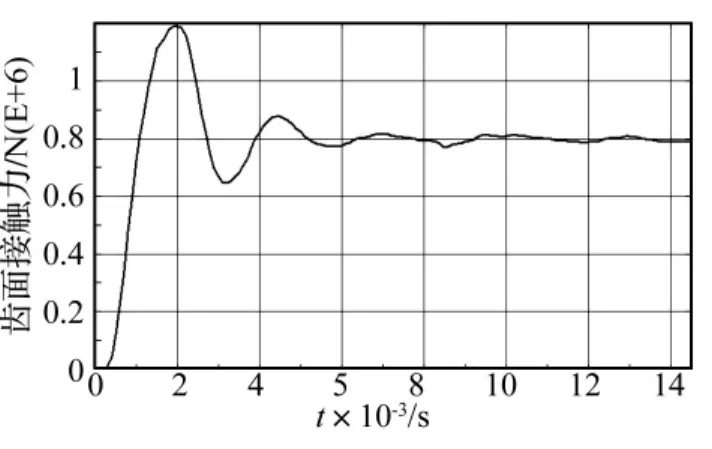
图9 模型Ⅲ的齿面接触力历程Fig.8 The tooth contact force time history of modelⅢ

3.2 惯性载荷对接触区域的影响

图10、图11 和图12 分别表示质量比为0.1∶1、1∶1和10∶1三种模型在相同时刻(0.0116 s)的小轮齿面应力云图。其中，图中的H22431、H21123、H34854分别表示三种模型当前时刻最大齿面应力所在单元。

对比三种质量比模型的齿面应力云图可知，齿面接触区均为类椭圆形。总体上看，随着质量比的增大，惯性载荷随之增大，接触椭圆的长轴半径即接触区宽度也逐渐增大。其中，质量比为0.1∶1为单齿接触，齿面最大接触应力位于齿面中间部位;1∶1模型为2齿接触，最大接触应力位置偏向齿顶;而随着惯性载荷的进一步增大，质量比为10∶1模型变为3齿接触，接触区更大，齿面最大接触应力出现在第三齿。

结合图10、图11和图12，对比不同质量比模型在相同位置(单元22311)的有效应力历程，分别如图13、图14及图15所示。其中，质量比为0.1∶1模型单元22311的最大应力为204.84 MPa;质量比为1∶1模型的最大应力为512.18 MPa;质量比为10∶1模型的最大应力为2195.8 MPa。可见，随着质量比即轮齿惯性载荷的增大，齿面接触应力增大。

图10 模型Ⅰ的大轮齿面应力云图Fig.10 Pressure pattern of pinion in modelⅠ

图11 模型Ⅱ的大轮齿面应力云图Fig.11 Pressure pattern of pinion in modelⅡ

图12 模型Ⅲ的大轮齿面应力云图Fig.12 Pressure pattern of pinion in modelⅢ

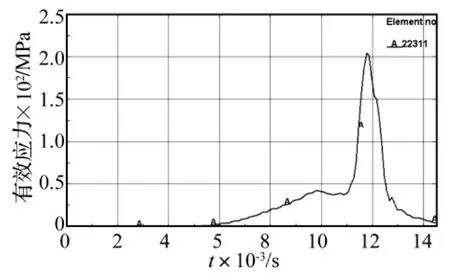
图13 模型Ⅰ齿面单元有效应力历程Fig.13 The effective stress time history of the surface element in modelⅠ

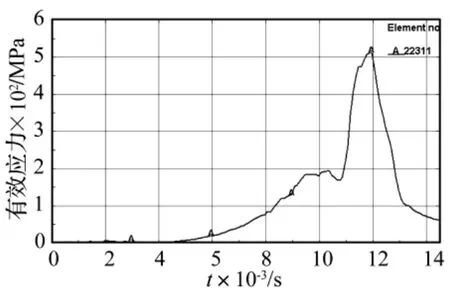
图14 模型Ⅱ齿面单元有效应力历程Fig.14 The effective stress time history of the surface element in modelⅡ

图15 模型Ⅲ齿面单元有效应力历程Fig.15 The effective stress time history of the surface element in modelⅢ

非线性动力分析程序用于工程计算，最大的困难是耗费机时过多，显式积分的每一时步，单元计算的机时占总机时的主要部分。采用单点高斯积分的单元计算可以极大地节省数据存贮量和运算次数，但是单点积分可能引起零能模式(沙漏)，需加以控制。根据LSTC公司的经验推荐，沙漏能与内能的比值小于10%是可以接受的。查看本算例的能量关系图，如图16所示。可以计算得到沙漏能平均值是内能平均值的2.91%，可见，该分析中单点积分引起的沙漏是可以忽略的。

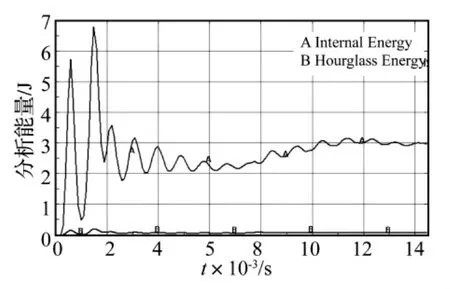
图16 沙漏能与内能对比示意图Fig.16 Comparison diagram of internal energy and hourglass energy

4 结论

(1)根据动力学原理和Lagrange乘子约束，提出了考虑惯性载荷的螺旋锥齿轮动态啮合分析有限元模型，为客观、准确地分析螺旋锥齿轮的动态啮合性能提供了必要的准备。

(2)惯性载荷对齿轮运动特性和齿面接触力的波动幅值和频率均有显著影响:随着惯性载荷的增大，齿面接触力的波动幅值增大，波动频率减小。

(3)惯性载荷对轮齿接触的接触区宽度、齿面接触应力以及最大应力位置有明显影响:随着齿轮惯性载荷的增大，接触区宽度增大，齿面接触应力增大。

［1］Wilcox L，Nowell G.Improved Finite Element Model for Calculating Stress in Bevel and Hypoid Gear Teeth［C］.AGMA 97FTM5，Nov.1997.

［2］李盛鹏，方宗德.弧齿锥齿轮齿根弯曲应力分析［J］.航空动力学报，2007，22(5):843 －848.

［3］张金良，方宗德.弧齿锥齿轮齿面接触应力分析［J］.机械科学与技术，2007，26(10):1268 －1272.

［4］Argyris J，Fuentes A，Litvin F L.Computerized integrated approach for design and stress analysis of spiral bevel gears［J］.Computer methods applied in mechanics and engineering，2002，191:1057 －1095.

［5］Litvin F L，Vecchiato D.Computerized developments in design，generation，simulation of meshing，and stress analysis of gear drives［J］.Meccanica，2005，40:291 －324.

［6］Robert F H，George D B.Comparison of Experimental and Analytical Tooth Bending Stress of Aerospace Spiral Bevel Gears［R］.NASA/TM 208903，1999.

［7］李 源，袁杰红.航空减速器准双曲面齿轮动态啮合仿真分析［J］.机械传动，2007，31(5):43 －44.

［8］北京理工大学ANSYS/LS－DYNA中国技术支持中心.ANSYS/LS-DYNA算法基础与使用方法［M］.北京;北京理工大学，1999.

［9］Zienkiewicz O C，Taylor K.L.The Finite Element Method，Fifth Edition［M］.Butterworth Heinemann，2000.

［10］唐进元，曹 康.含过渡曲面的弧齿锥齿轮齿面精确建模［J］.机械科学与技术，2009，28(3):317 －321.