准双曲面齿轮箱响应分析及动力优化

林腾蛟，李应超，杨妍妮

(重庆大学 机械传动国家重点实验室，重庆 400030)

准双曲面齿轮传动承载能力高、传动比大、运转平稳，已在航空工业、汽车工业及矿山机械中广泛应用，并逐渐向高速、重载和轻量化方向发展。高速重载齿轮传动常常会产生较大的振动噪声和动载荷，直接影响齿轮系统的可靠性和动态性能。因此，以齿轮系统动态响应(如位移、速度、加速度、应力等)为目标或约束的动力优化设计逐渐引起人们的关注。

目前，对于锥齿轮系统振动分析，国内外学者多采用集中参数法建立齿轮系统动力分析模型，分析其固有特性和动态响应［1－4］，在此基础上进一步研究了分岔与混沌等非线性动态特性［5－6］。随着数值仿真技术的发展，有限元法在锥齿轮的齿面接触分析中得到广泛应用，通过建立齿轮副动力接触有限元分析模型［7－8］，模拟齿轮动态激励，进而研究齿轮系统的振动特性［9］。齿轮系统动力优化可分为模态参数优化和动力响应优化两方面，迄今关于传动系统动力优化的工作大部分都集中于具有频率约束的结构质量极小化或者避免共振问题上［10－11］，以结构动态响应(动应力、动位移等)为约束的动力优化设计工作也有所开展［12］，但相关研究较少。

本文以准双曲面齿轮箱为研究对象，综合考虑轮齿啮合变形、轴的弯曲变形及轴承支撑刚度，建立包括齿轮、轴、轴承的准双曲面齿轮传动非线性动力接触有限元分析模型，利用ANSYS/LS－DYNA仿真计算轴承动态支反力;将轴承动态支反力作为箱体的输入载荷，对准双曲面齿轮箱进行瞬态动力分析;以加速度响应均方根值最小为优化目标，箱体结构参数为设计变量，以静态应力、位移及箱体体积为约束条件，建立准双曲面齿轮箱动态响应优化模型，借助ANSYS求解动态响应优化模型，得到箱体最优设计参数。

1 齿轮传动系统动态支反力模拟

1.1 LS-DYNA显式动力学算法

根据最小势能原理，运动微分方程的弱形式为［13］:

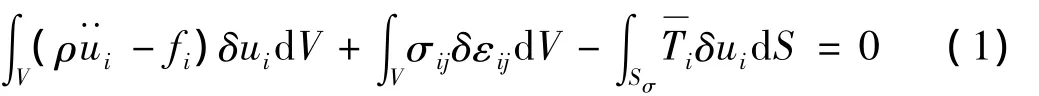
式中:ρ为质量密度;ui为节点位移张量;fi为体力张量;δui为虚位移张量;σij为节点应力张量;δεij为节点虚应变张量;Sσ为外力边界;为面力张量。

将整个结构划分为一系列离散单元，用各单元的势能变分之和来近似的总势能，为:

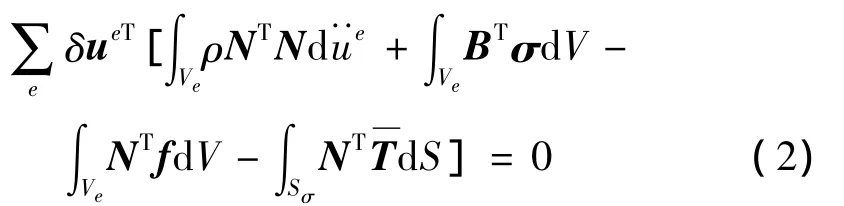
式中:ue为位移向量;N为形函数;B为应变矩阵;σ为应力向量;f为体力向量;为面力向量;Ve为单元体积。

改写上式可得离散化运动方程为:

其中:M为总体质量矩阵:

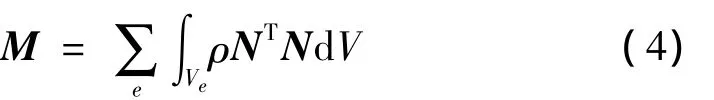
F为应力散度向量:

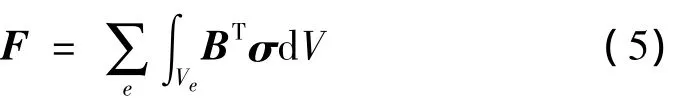
P为总体节点外载荷向量:

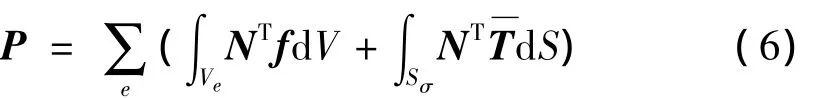
LS－DYNA采用沙漏粘性阻力来解决沙漏问题。将各节点的沙漏粘性阻尼力集成可得结构沙漏粘性阻尼力向量H，同时考虑阻尼影响(阻尼矩阵C)，并引入接触力R，则动力接触问题离散化运动方程为:

方程(7)采用显式中心差分法求解，其基本格式为:

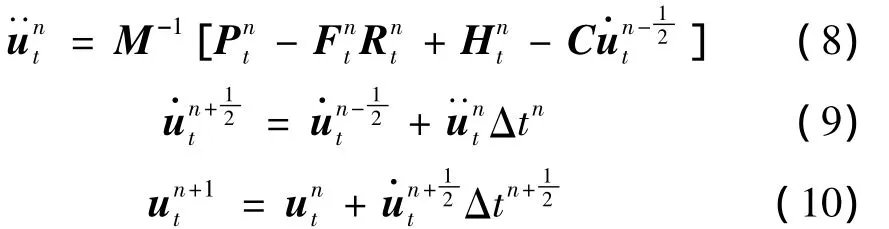
1.2 准双曲面齿轮传动动力接触有限元模型

准双曲面齿轮副的几何参数如表1所示，材料弹性模量 E=2.06 ×1011N/m2，泊松比 v=0.3，材料密度ρ=7.8×103kg/m3。在UG中建立齿轮箱各传动部件的实体模型和虚拟装配模型，而后导入ANSYS/LS-DYNA中，并将大齿轮和轮毂间的螺栓联接以及轮毂与轴过盈配合视为刚性联接，忽略键槽、倒角和退刀槽的影响。

表1 准双曲面齿轮副几何参数Tab.1 Geometric parameters of hypoid gears

建立准双曲面齿轮传动系统动力接触有限元模型时，采用SOLID164单元将齿轮、轴、轴承划分为六面体实体单元，并将单元属性设置为全积分单元算法，进行沙漏控制。由于SOLID164单元不具有旋转自由度，将输入轴和输出轴与法兰联接的轴段表面定义为刚性壳体单元SHELL163，以便施加转速和转矩进行动力分析。准双曲面齿轮传动系统的有限元网格如图1所示，共计节点数为114424，单元数为74205。图中轴承滚柱支撑刚度用截面梁来模拟，轴承外圈表面施加固定位移约束。大、小齿轮之间以及轴与轴承之间共建立5组接触对，接触类型为自动面面接触。输入齿轮轴轴颈处施加转速3000 r/min，输出轴轴颈处施加负载转矩1114 N·m。

图1 准双曲面齿轮传动系统有限元网格Fig.1 Finite element mesh of hypoid gear transmission system

计算模型中同时考虑了齿轮时变啮合刚度、轮齿变形、轴承变形及轴的弯曲变形等的影响，能较为真实地模拟齿轮传动系统的运转过程。

1.3 轴承动态支反力数值模拟

采用显式动力学算法对准双曲面齿轮传动系统进行动力接触分析，得出齿轮传动过程中四个轴承处的动态支反力，图2为输入轴靠近主动轮端轴承的动态支反力曲线。由图可知，由于5 ms之前处于加载阶段，轴承支反力不稳定，5 ms之后轴承支反力呈现出一定的周期性，大周期为20 ms，小周期为2.85 ms，这与主动轴的转频50 Hz、齿轮啮合频率350 Hz相吻合。图3给出了输出轴靠近输出端轴承的动态支反力曲线。

图2 输入轴轴承动态支反力Fig.2 Dynamic support reaction of bearing at input shaft

图3 输出轴轴承动态支反力Fig.3 Dynamic support reaction of bearing at output shaft

2 齿轮箱动态响应仿真与试验

2.1 齿轮箱动态响应数值仿真

在ANSYS中利用APDL语言建立准双曲面齿轮箱箱体的参数化模型，采用四面体单元进行网格自动划分。图4为准双曲面齿轮箱箱体的有限元网格，共计21629个节点，91300个单元。图中给出了部分计算点的位置，标线下方为箱体对面相应节点位置。

图4 准双曲面齿轮箱箱体的有限元网格Fig.4 Finite element mesh of hypoid gearbox housing

将各轴承动态支反力作为输入载荷施加在箱体轴承孔上，利用ANSYS的瞬态动力分析模块，采用完全法对箱体进行动力响应分析。时间步长为Δt=0.2 ms，求解总时间为100 ms。表2给出了箱体测点处各节点的加速度均方根值，图5给出了箱体外表面节点10053的振动加速度响应曲线。

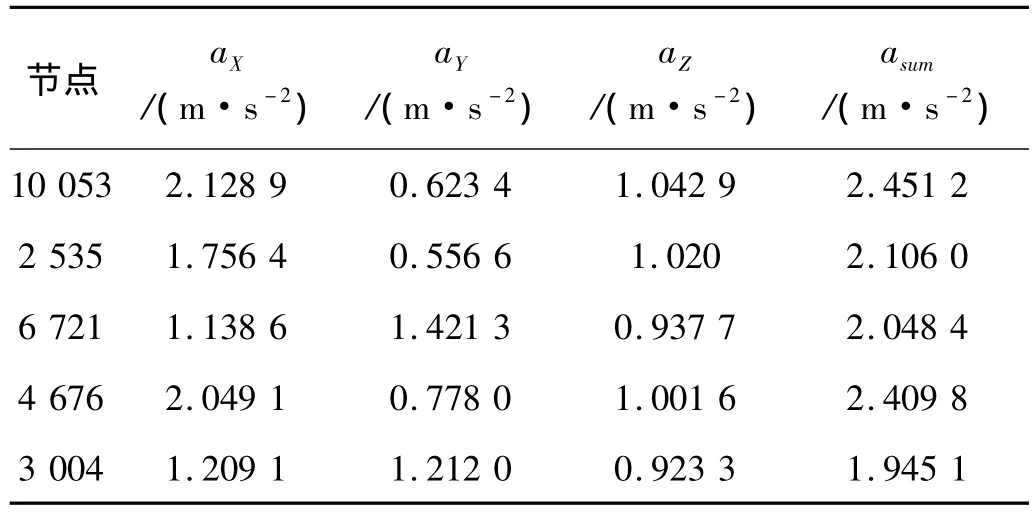
表2 各节点的加速度均方根值Tab.2 The acceleration root－mean square values of nodes

2.2 齿轮箱动态响应测试

图6为准双曲面齿轮箱动态性能试验台，测点布置见图4。试验装置包括直流调速电动机、待测齿轮箱、转矩转速传感器与磁粉制动器，通过改变输入转速和负载，可获得不同转速和负载工况下齿轮箱各测点的法向振动加速度响应。

对比ANSYS计算所得的齿轮箱振动加速度与各测点的加速度实测结果，两者在幅值大小上基本一致，表明了齿轮箱动力有限元计算模型的准确性。图7给出了轴承座附近测点1的X、Y和Z向振动加速度响应曲线。

图5 节点10053的振动加速度曲线Fig.5 Vibration acceleration curve of node 10053

图6 准双曲面齿轮箱动态性能试验台Fig.6 Dynamic performance test bench of hypoid gearbox

3 齿轮箱动态响应优化设计

3.1 ANSYS优化设计方法

最优化问题在数学上可表达如下:

式中:f(x)为目标函数;x=(x1，x2，…，xn)T为结构系统的设计变量，n为设计变量个数;gi、hi、wi为优化过程中的状态变量，带上标U的是状态变量上限，带上标L的是状态变量下限;m1，m2，m3分别为状态变量个数。

对于此优化问题的数学模型的求解，工程上有多种计算方法。ANSYS零阶方法首先用近似方程式将目标函数和状态变量表示为:

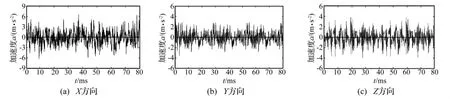
图7 测点1的振动加速度响应曲线Fig.7 Vibration acceleration curve of test point 1

式中:e为近似函数误差项。

上述复杂近似表达式可由带交叉项的二次多项式表示，此时不等式约束转换成等式约束形式。以目标函数为例:

式中:系数ai和bij由加权最小二乘法确定。

然后，用罚函数法将约束最优化问题转换成非约束最优化问题。即:

式中:X为设计变量约束的罚函数;G、H、W为状态变量约束的罚函数，pk为响应面参数。引入目标函数参考值f0确保单位的相容性。

用序列无约束最小化技术(SUMT)求解方程(14)。求解过程中，响应面参数不断增加(p1＜p2＜p3＜…)以获得精确、收敛的优化结果。优化迭代过程直到满足收敛条件或达到指定优化次数后完成。

3.2 设计变量

齿轮箱动态响应优化一般是通过对动载荷作用下箱体结构参数的寻优，达到降低齿轮箱振动噪声的目的。由于选用太多设计变量会使得收敛于局部最小值的可能性增加，故仅以式(15)中的15个箱体结构参数为设计变量，各参数的含义及初始值设定参见表3。

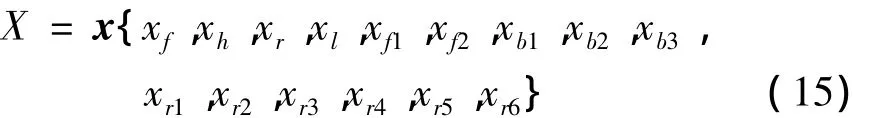
3.3 目标函数

一般情况下，齿轮系统动载荷与振动加速度均方根值之间有较大一致性，因此可将箱体各节点振动加速度最小作为目标函数以衡量齿轮传动系统的稳定性。为了简化目标函数，选取振动加速度大，且对齿轮系统传动稳定性和动态性能影响较大的节点作为优化对象。本文选取箱体外表面的节点10053、2535、6721、4676和3004，以其振动加速度均方根值的大小来近似衡量整个齿轮箱振动状况，将动态响应优化目标函数定义为:

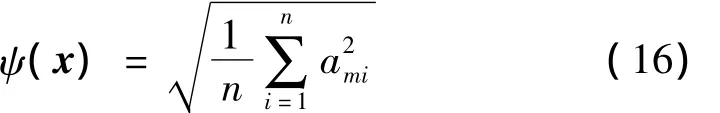
式中，ami为各节点的振动加速度均方根值，n为节点个数。

3.4 约束条件

齿轮箱动态响应优化时，同时应满足静态设计要求的约束条件，即静态应力和位移，如式(17)～式(18);还应尽量减小箱体的体积或重量，如式(19)。

式中:σmax、umax、Vsum分别为设计空间内取任意一组设计参数时，计算所得最大等效应力、最大综合位移和箱体体积;σs为箱体材料屈服极限;u0为箱体允许的最大静态综合位移;V0为初始设计时箱体的体积。

3.5 箱体动态响应优化结果

用零阶方法求解优化模型，优化迭代在24步时收敛，得到箱体最优设计参数，如表3所示。图8为目标函数随迭代步数的变化曲线，图9为优化后节点10053的加速度响应曲线。表4给出了优化后各节点的振动加速度均方根值，表5为优化前后箱体的性能指标，在保证满足静强度要求的前提下，体积略有减小，振动加速度均方根值由原来的2.21 m/s2减小到1.56 m/s2，减小了29.4%，优化效果比较明显。

表3 箱体优化设计变量Tab.3 Optimum design variables of housing

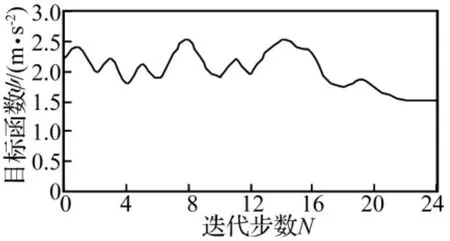
图8 目标函数变化曲线Fig.8 Variation curve of object function

图9 优化后节点10053加速度响应曲线Fig.9 Acceleration responses of node 10053 after optimization

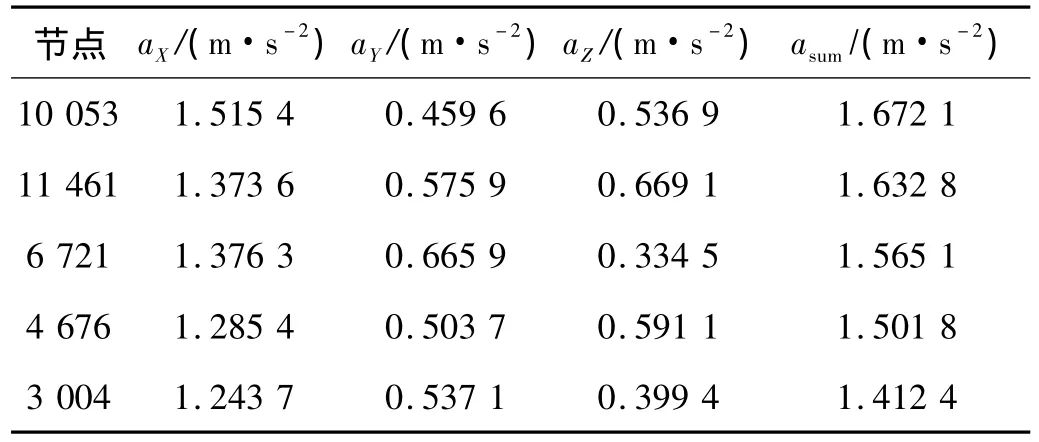
表4 优化后各节点的加速度均方根Tab.4 The acceleration root-mean square value of nodes after optimization

表5 优化前后箱体性能指标对比Tab.5 Performance comparison of housing before and after optimization

4 结论

(1)通过准双曲面齿轮传动动力接触有限元分析得出轴承动态支反力，其周期性与传动轴的转频及齿轮的啮合频率相吻合。

(2)对准双曲面齿轮箱进行动态响应有限元分析，得到箱体各节点的振动加速度，与实测值相比，两者在幅值大小上基本一致。

(3)以加速度均方根值最小为目标，对箱体进行动力优化，得到箱体最优设计参数。在保证满足静强度要求的前提下，优化后箱体体积略有减小，振动加速度均方根值减小了29.4%，优化效果较为明显。

［1］杨宏斌，高建平，方宗德，等.准双曲面齿轮非线性振动分析［J］.汽车工程，2000，22(1):51－54.

［2］Cheng Y，Lim T C.Vibration analysis of hypoid transmissions applying an exact geometry-based gear mesh theory［J］.Journal of Sound and Vibration，2001，240(3):519－543.

［3］Tanaka N，Ohno K，Innami T.Dynamic load on spiral bevel gears［C］.The JSME International Conference on motion and Power Transmissions，Fukuoka，Japan，2001:27 －32.

［4］Li M，Hu H Y.Dynamic analysis of a spiral bevel-geared rotor-bearing system［J］.Journal of Sound and Vibration，2003，259(3):605－624.

［5］杨先勇，周晓军，林 勇，等.螺旋锥齿轮间隙非线性系统的分岔与混沌［J］.振动与冲击，2008，27(11):115－119，125.

［6］杨先勇，周晓军，胡宏伟，等.螺旋锥齿轮非线性振动特性及参数影响［J］.浙江大学学报，2009，43(9):505－510.

［7］林腾蛟，杨妍妮，李润方，等.弧齿锥齿轮传动内部动态激励数值仿真［J］.重庆大学学报，2009，32(6):609－613.

［8］马雪洁，谢刚，王小林.基于ANSYS/LS-DYNA的准双曲面齿轮动力学接触仿真分析［J］.机械传动，2005，29(6):51－53.

［9］王立华，黄亚宇，李润方，等.准双曲面齿轮系统振动的理论分析与试验研究［J］.机械设计与研究，2007，23(2):65 －67，73.

［10］符代竹，秦大同，魏治国，等.混合动力汽车变速器齿轮轴的模态优化［J］.重庆大学学报，2005，18(12):15 －17.

［11］Dylejko P G，Kessissoglou N J，Tso Y，et al.Optimisation of a resonance changer to minimise the vibration transmission in marine vessels［J］.Journal of Sound and Vibration，2007，300(1－2):101－116.

［12］郑光泽，李润方，林腾蛟.高速重载齿轮传动系统动态响应优化设计［J］.机械设计，2005，22(6):27－29.

［13］尚晓江，苏建宇.ANSYS/LS-DYNA动力分析方法与工程实例［M］.北京:中国水利水电出版社，2006.

［14］荣见化，郑健龙，徐飞鸿.结构动力修改及优化设计［M］.北京:人民交通出版社，2002.