经验非线性涡激力模型参数识别

周 涛，朱乐东，3，郭震山

(1.同济大学 土木工程防灾国家重点实验室，上海 200092;2.同济大学 桥梁工程系，上海 200092;3.桥梁结构抗风技术交通行业重点实验室，上海 200092)

实践表明，许多大跨度桥梁在较低风速时，都发生过涡激共振。如英国的Second Seven桥［1］、日本的东京湾大桥［2］、丹麦的 Great Belt桥东引桥［3］、巴西的Rio-Niteroi桥［4］都出现过大幅度的涡振。涡激共振是一种带有强迫和自激双重特性的自限幅风致振动现象［5］:在一定风速范围内，当旋涡脱落频率与桥梁某一固有频率接近时，便会发生涡激共振;而此时桥梁的振动又会对旋涡脱落形成反馈，使一定风速范围内旋涡脱落频率“锁定”在固有频率附近，不再随风速变化。

而“锁定”现象的存在，使原先周期性的强迫涡激力，附加了与桥梁本身运动有关的复杂的非线性涡激力项，这使得涡振共振进入流固耦合作用的范围，在理论上要获得涡激力的解析解非常困难。在涡激共振的研究过程中，人们提出的半经验模型虽然不能从原理上理解旋涡产生、发展的机理过程，但可以在适当选择模型参数后较准确地描述钝体涡激振动现象。并且由于实际桥梁的竖弯和扭转基频都相差一定数量，在一定的涡激共振风速范围内，涡激力一般只能激发起某一阶固有模态的共振，即竖弯、扭转涡振振型独立，使得基于单自由度振动的涡激力模型有了实际意义。

到目前为止，所建立的单振子涡激振动模型主要有简谐力模型、升力振子模型、经验线性模型、经验非线性模型、广义经验非线性模型等。本文的试验是在同济大学TJ－1号风洞中，以象山港大桥初始设计阶段节段模型为例，用激光位移计采集涡激共振竖向位移响应随时间变化曲线后，基于涡激共振典型表现—拍振［7］，研究Scanlan涡激共振经验非线性模型的中气动参数识别，并得到 Scanlan非线性涡激力。最后，对识别精度进行了评价。节段模型系统质量按照文献［5，6］所述方法设计。

1 单自由度涡振经验非线性模型响应求解

Scanlan和Ehsan在涡振经验线性模型的基础上，通过增加了一个非线性的气动阻尼项，把涡激力的描述引入到非线性的范围内，提出了经验非线性模型:

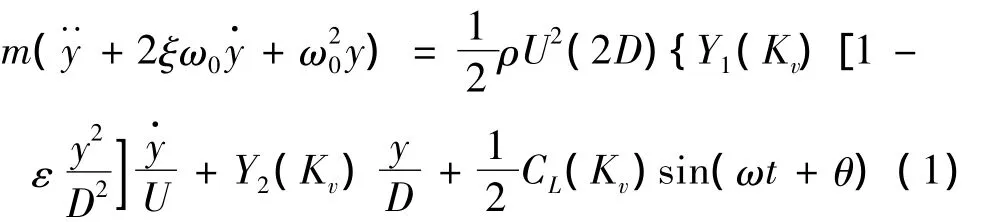
其中:m为系统质量;ω0为结构竖弯振动频率;ξ为阻尼比;ρ为空气密度;U为来流风速;D为结构横风向尺寸;y为涡激共振竖向响应;约化频率Kv=ω0D/U;系数Y1、Y2、CL、ε 都是约化频率 Kv的函数，需要本文从风洞试验数据中分析得到。

为应用广义谐波函数KBM法求解Scanlan经验非线性模型涡振响应，要使式(1)满足如下形式:

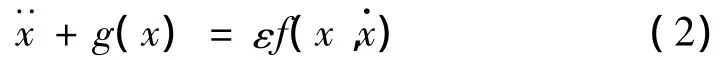
为此，首先无量纲化式(1)，令η=y/D，s=Ut/D，=dη/ds，并引入 mr=ρD/m，则式(1)变为:

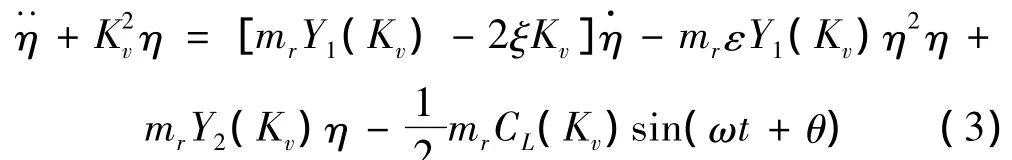
假定式(3)满足式(2)的形式，即将式(3)写为:

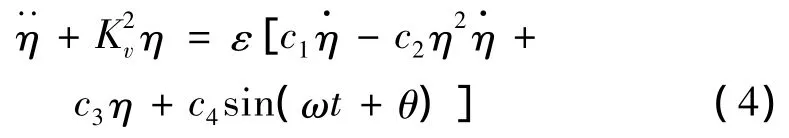
对比式(3)、式(4)可以得到:

此外，引入失谐参数σ来定量的描述K与约化频率Kv的逼近程度，σ满足条件:

则式(4)变为:

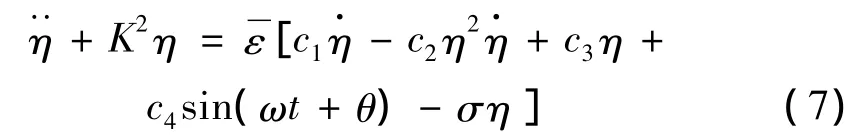
此时，单自由度钝体竖向涡激振动方程(7)为一Van der Pol型非线性非自治方程，其原理是基于在位移为X轴、以速度为Y轴的相平面内存在一个闭合的“极循环”，可以采用KBM法求得共振一次近似解:

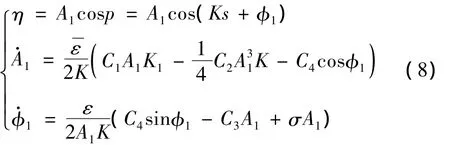
对于式(8)第二式，取其一阶近似解:

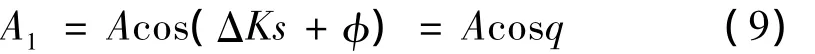
从式(8)第二式、第三式中消去φ1可以得到:

其中:

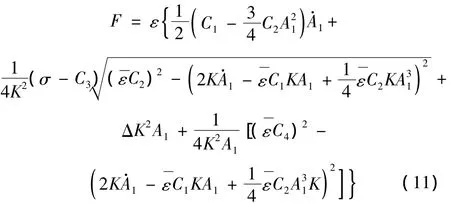
在此，引入缓变参数［8］的概念，即认为在一个周期内为常数，则可以得到:

将式(8)第一式、式(10)、式(11)代入式(12)、式(13)中可以得到:

其中，β为稳定振幅。

为了简化方程，引入变量:

将其代入式(14)、式(16)可以得到:

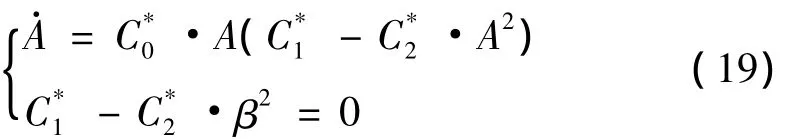
求解可以得到:

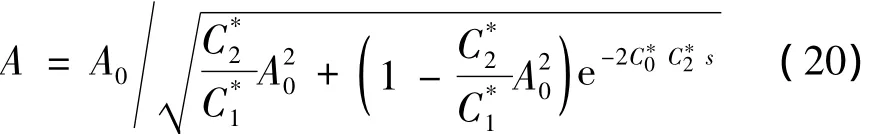
此外，利用缓变参数的假定以及式(9)，可以得到:

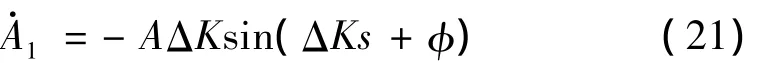
联立式(8)第二式可以得到s=0时:

式中，φ0、φ0分别是对应于 ΔK、K的初相位。

2 风洞试验及参数识别

2.1 风洞试验

象山港大桥初步设计阶段主桥为跨度688 m的钢箱梁双塔斜拉桥，跨海长度约6118 m，主梁宽31.6 m，高3.5 m。其主梁标准横断面图见图1。

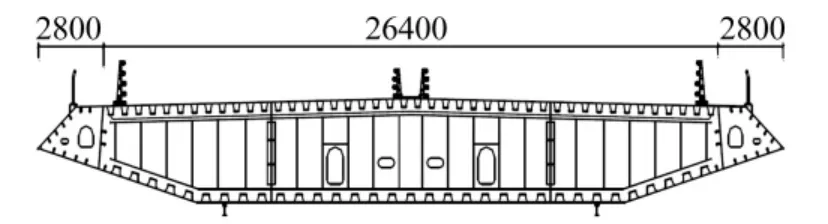
图1 主梁标准横断面图Fig.1 The standard cross section of main gird

试验节段模型主梁尺寸为1.70 m×0.582 m×0.0636 m，模型安装见图2。试验在TJ－1号风洞均匀流场中进行，采用激光位移计(图3)采集模型发生竖弯涡激共振响应随时间变化曲线;并利用四个一维梁式应变测力天平同步测得模型所受合力(图4、图5)。

图2 试验节段模型的安装Fig.2 Installation of the section model

图3 激光位移计的安装Fig.3 Installation of the laser displacement sensor

图4 一维梁式应变测力天平Fig.4 Beam-type strain force balances of one-dimension

试验过程中测得系统竖弯阻尼为0.28%，结构的竖弯基频为3.52 Hz，扭转基频为7.25 Hz。模型发生涡激共振风速区间为 3.32 m/s ～ 4.38 m/s，3.86 m/s时振幅最大，此时位移响应随时间变化曲线见图6，卓越频率为3.53 Hz(见图7)，与结构自身的竖弯基频十分接近。发生涡激共振初始风速时的Strouhal数为0.098。

2.2 参数计算

为按照第二节中所述方法识别Scanlan经验非线性模型中的气动参数，首先按照η=y/D、s=Ut/D对图6所示的竖向响应进行无量纲化处理，从得到的η－s曲线中可以很容易的求得折减频率K、ΔK;以及对应的初始相位φ0、φ0;稳定状态振幅β;初始位移A0。然后由式(18)可求得;再由第一次近似解式(20)，取初值 A0＞β，即按照“从衰减到共振”［8］用最小二乘求解、;之后联立式(16)～式(18)、式(22)即可 C1～C4、ε五个参数，最后代入式(5)即可得到需要识别的气动参数，如表1所示。

图5 测力天平的安装Fig.5 Installation of the force balances

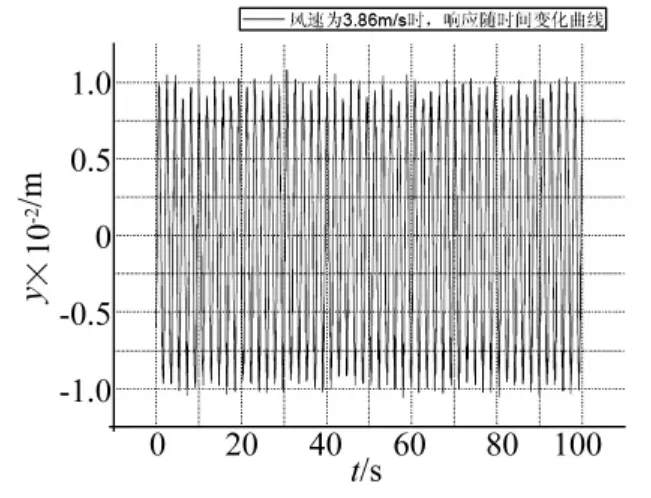
图6 涡振响应随时间变化曲线Fig.6 The time varying curve of the VIV response

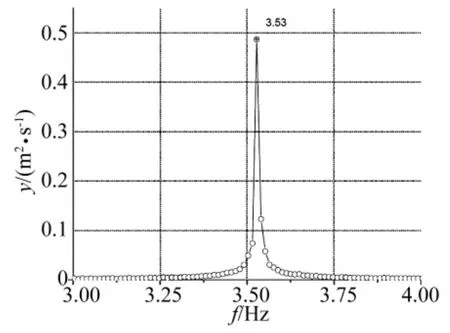
图7 涡振响应频谱分析Fig.7 The power spectrum of the VIV response

表1 Scanlan经验非线性模型参数识别结果Tab.1 Parameters of Scanlan’s nonlinear empirical model

将表1的参数值代入式(1)中，即可得到Scanlan非线性涡激力，如图8所示，其频谱分析如图9所示。

2.3 参数识别精度评价

从图9中可以看出，涡激力功率谱中除了有与涡激共振响应相同的卓越频率3.53外，还有另外一个卓越频率0.56。本文分别通过以下两种方法，对基于广义谐波函数KBM法及缓变参数的假定来识别得到Scanlan涡激共振经验非线性模型参数精度做出评价。

2.3.1 反求响应进行验算

为验证识别精度，用识别得到的Scanlan非线性涡激力，利用Newmark β法反求结构的响应，并与实际测得的结构响应进行比较，结果如图10所示。

图8 Scanlan非线性涡激力(纵桥向每延米)Fig.8 Scanlan’s nonlinear vortex-induced force

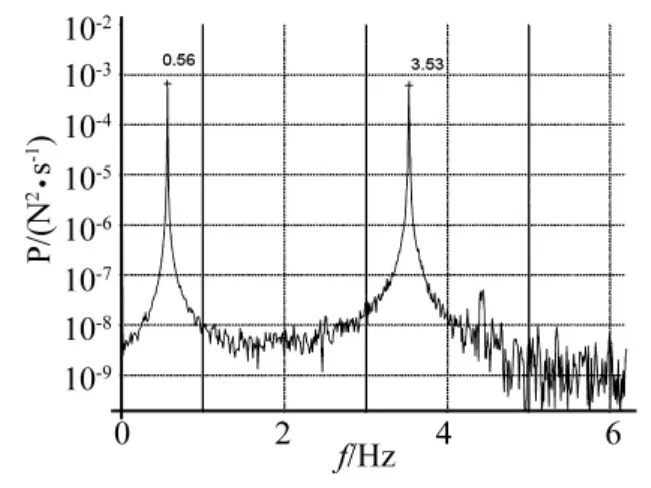
图9 Scanlan非线性涡激力频谱分析Fig.9 The spectrum of Scanlan’s nonlinear vortex-induced force

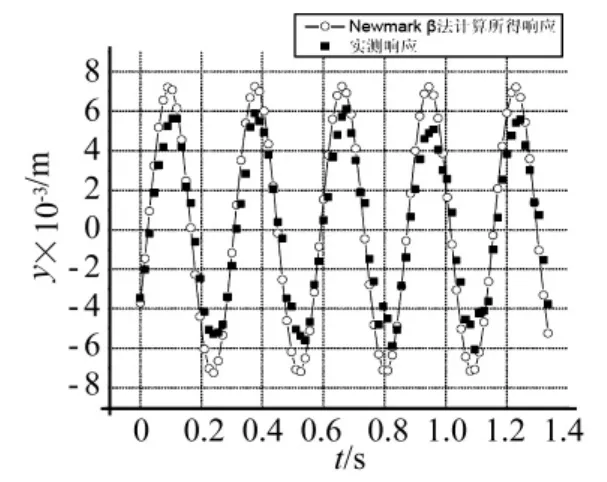
图10 实测响应与Newmark β计算所得响应比较Fig.10 Comparison between the fields measured response with the response calculated according to the Newmark β method

由图10可以看出，由Newmark β法反求的结构响应最大振幅比实测的最大振幅略微偏大。将Newmark β反求的响应进行频谱分析，如图11所示，可见虽然依然存在同图9所示的幅值相同的两个卓越频率，但较低频率0.56的影响非常小，可以忽略。

2.3.2 提取实测涡激力与Scanlan非线性涡激力比较为验证利用广义谐波函数KBM法及缓变参数的假定［7，8］所识别的参数的精度，更直接的方法是从试验中天平所测得的合力信号中提取出实测的涡激力，与利用本文第一节所述的识别方法得到的Scanlan非线性涡激力进行比较。

提取作用在节段模型上实测涡激力，可以通过从天平测到的合力中扣除模型的惯性力得到，结果如图12所示。此时，从图8以及图12中，都可以看出模型所受的涡激力具有与竖向位移响应相同的形式。

对实测涡激力的进行功率谱分析，结果如图13所示。从图13中可以看出，从天平采集的合力中提取的涡激力，或者称为实测得到的涡激力功率谱中，仅有与涡激共振响应频谱中相同的卓越频率3.53。这不同于利用广义谐波函数KBM法及缓变参数的假定所识别的参数得到的Scanlan非线性涡激力功率谱。此时可以判定，这个额外的卓越频率是在利用文献［7，8］所阐述的方法进行识别的过程中引入的，实际涡激力频谱中并不存在。

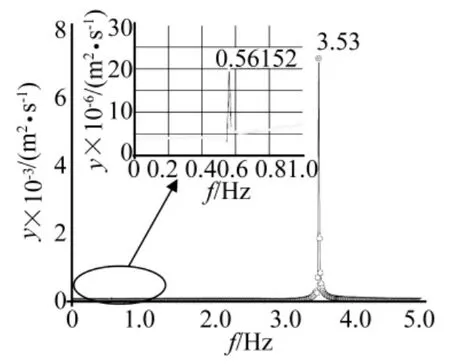
图11 Newmark β计算所得响应功率谱Fig.11 The power spectrum of the response which was calculated according to the Newmark β method

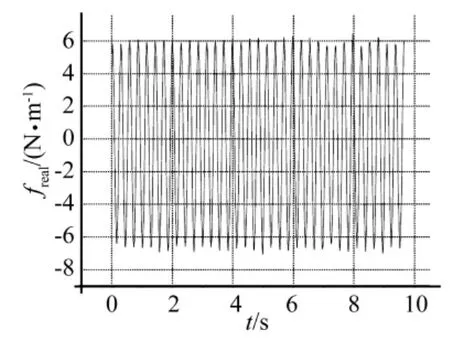
图12 天平采集合力中提取的实测涡激力(纵桥向每延米)Fig.12 The self-excited VIV force extracted from the total force collected by the one-dimensional balances

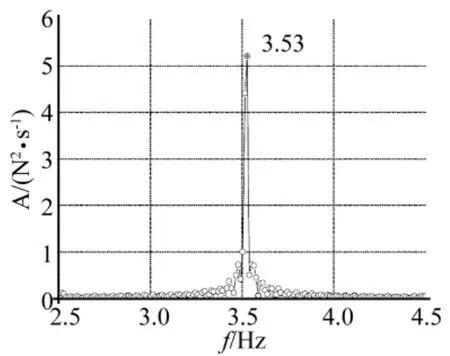
图13 从天平测得的合力中提取的涡激力功率谱Fig.13 The power spectrum of the self-excited VIV force extracted from the total force

3 结论

本文以象山港大桥初步设计阶段节段模型为例，在同济大学TJ－1号风洞均匀流场中进行了竖弯涡激共振试验，利用激光位移计采集了模型发生涡激共振时的响应随时间变化数据，并同时利用一维梁式应变测力天平同步采集了模型所受的合力。然后利用广义谐波函数KBM法对Scanlan经验非线性模型进行处理，并引入了缓变参数的假定，从而利用位移响应随时间变化曲线识别出其中的气动参数，得到Scanlan经验非线性涡激力，并对识别的参数做出评价。在参数识别及精度评价过程中，得到的主要结论有:

模型所受的涡激力具有与竖向位移响应相同的形式，即周期性振动。

利用广义谐波函数KBM法及缓变参数的假定［7，8］识别得到的Scanlan非线性涡激力功率谱中，存在除与竖向位移响应相同的卓越频率以外的卓越频率。

利用Newmark β法对利用第二节所述方法识别得到的Scanlan非线性涡激力，反求得到的响应比实测响应值偏大。

从模型所受的合力中提取的实测涡激力功率谱中，仅存在与竖向位移响应相同的卓越频率。

在利用广义谐波函数KBM法及缓变参数的假定识别参数的过程中，结果对初始条件及舍入误差敏感;同时，综合2.3.1 节以及2.3.2 节的精度评价过程，利用广义谐波函数KBM法及缓变参数的假定识别得到的Scanlan非线性涡激力引入了实际中并不存在的额外的卓越频率，Scanlan经验非线性模型中参数识别精度有待于进一步改进，比如在更深一步的研究中，可以直接采用同步测得模型所受的合力及涡激共振响应数据，然后从合力中提取出实测得涡激力，用非线性拟合的方法进行气动参数识别。

［1］Macdonald J H G，Irwin P A，Fletcher M S.Vortex-induced vibrations of Second Severn Crossing cable stayed bridge-fullscale and wind tunnel measurements［J］.Structures ＆Buildings，2002，152(2).

［2］YoZo Fujino，Yoshitaka Yoshida.Wind-induced vibration and control of trans-Tokyo Bay Crossing Bridge［J］.Journal of Structural Engineering，2002，1012－1025.

［3］陈政清.桥梁风工程［M］.北京:人民交通出版社，2005.

［4］Ronaldo C B，Ichele S P.Reduction of vortex induced oscillations of Rio-Niteroi bridge by dynamic control devices［J］.Journal of Wind Engineering and Industry Aerodynamics，2000，84:273 －288.

［5］朱乐东.桥梁涡激共振试验节段模型质量系统模拟与振幅修正方法［J］.工程力学，2005，22(5).

［6］朱乐东，项海帆.桥梁颤振节段模型质量系统模拟［J］.结构工程师，1995，(04).

［7］Li Mingshui He Dexin.Parameter identification of vortex induced forces on bluff bodies［J］.ACTA Aerodynamic Sinica，1995，13(4).

［8］Ehsan F，Scanlan R H.Vortex-induced vibration of flexible bridge［J］.Journal of Engineering Mechanics，1990，116(6).