竖直向上传播剪切波作用下边坡动力响应规律
2011-06-01柴红保
柴红保 ,曹 平,林 杭
(1. 中南大学 资源与安全工程学院,湖南 长沙,410083;2. 湖南科技大学 能源与安全工程学院,湖南 湘潭,411201)
爆破和地震触发边坡失稳的动力问题历来是岩土工程和地震工程中关心的重要问题之一[1-2],我国相当多的大型基础设施如南水北调西线、三峡工程等水利枢纽工程以及山区高速公路和铁路客运专线都涉及多山地、多地震的地理地质环境,不可避免地带来了大量和地震作用有关的边坡稳定性问题,岩土边坡在动力作用下的稳定性问题日趋突出。研究动荷载作用下边坡动力响应特征和变化规律[3-10],提出稳定性分析方法和控制手段是工程界迫切需要解决的问题,也是岩石动力学研究的主要内容之一。据文献[7]报道,1971年美国Davis等在SanFemando地震的余震测量中,发现山顶的地震加速度比山脚的地震加速度成倍增加;卡格尔山山顶和山脚2点的强余震速度观测记录表明:山顶上地震持续时间显著增长,放大效应显著,并且位移、速度和加速度的放大效应不同;Gazetas[11]斜坡地震效应研究结果表明:(1) 斜坡上的地震烈度相对于谷底增加1°左右;(2) 在角度超过15°的圆锥状山体上部点的位移幅值与下部点的位移幅值相比,其局部谱段值增加高达 7倍;(3) 黄土阶地的幅值比底部的大4倍左右,比离开坡阶边缘25 m的水平面处大2倍左右。大量数值模拟结果表明边坡顶部对振动的反应幅值与边坡底部相比存在明显的放大现象(垂直向放大),坡的边缘部位对振动的反应幅值与内部(处于同一高度上的 2点比较)相比也存在放大现象(水平向放大)[7-10]。FLAC3D软件能够分析非线性动力学问题,被应用于岩土开挖、边坡稳定性及地震动力响应分析等诸多领域。在此,本文作者利用FLAC3D中的动力分析模块进行了大量的数值模拟,对边坡在地震作用下的动力响应规律(主要是速度响应和位移响应)以及地震动参数对动力响应的影响进行研究。
1 边坡动力分析模型及边界条件
1.1 计算模型
为了探讨边坡地震动力响应的一般规律,选择 3个不同尺寸的模型进行数值模拟,模型的尺寸(长×宽×高)分别为 1 400 m×510 m×1 m,1 400 m×680 m×1 m和1 400 m×900 m×1 m。边坡高H分别为210,380和600 m,坡角α=50°。边坡材料弹性模量为2 GPa,密度为2 700 kg/m3,泊松比为0.27。计算模型如图1所示。
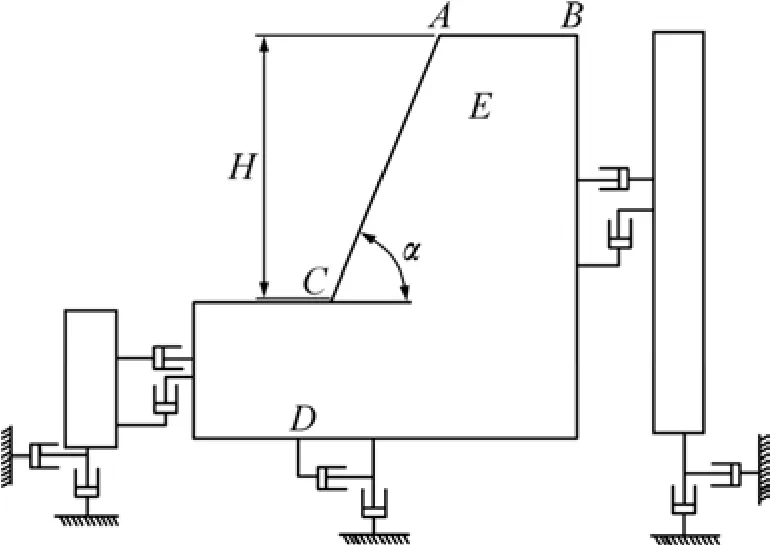
图1 边坡动力学数值模型Fig.1 Slope model for dynamic analysis
1.2 边界条件
在 FLAC3D动力模块中,边界条件设置有远置人工边界(截断边界)、静态(黏滞)边界和自由域。远置人工边界对入射波起着完全反射的作用,既不传播也不吸收任何能量。在动力体系中,这样被限制的能量会导致结果严重失真。为使边界对计算结果产生的影响变小,要求把模型的边界取得足够远,把模型的范围取得足够大,从而使边界反射的影响尽可能小。但是,边界设置过远会使数值计算困难。静态(黏滞)边界是在边界的法向和切向分别设置1个黏滞壶来消除边界对波的反射作用。该边界能够吸收入射波能量的一半,对于入射角大于 30°的波吸收效果比较显著,对于入射角小于 30°的波吸收效果不明显,但仍可以吸收一部分,此边界的有效性在有限单元法和有限差分法动力学分析中都得到了证明。自由域可以替代远场区域对模型的作用,当平面波向上传播的过程中没有发生变形时,自由域网格的作用相当于无限介质的作用,如果主网格(材质)均匀且没有地面建筑物,自由域的网格反应和主网格反应是一致的,此时,自由域网格和主网格间的黏壶体不起作用;若主网格上面有建筑物,则自由域的网格反应和主网格反应不一致,此时,自由域网格和主网格间的黏壶体就会像静态边界一样吸收能量。在模型边界设置自由域不必考虑模型边界对波的反射吸收问题,它完全起到了被截断的区域对模型的作用。
本文分析模型中采用自由域。图1所示是边坡在地震波作用下分析模型的边界条件设置情况。对于黏滞边界条件,边界条件的输入必须采用应力时程。速度时程边界条件可以转换为应力时程, 对于加速度时程可通过积分转化为速度时程,再转换为相应的应力输入。应力边界条件的转化为:
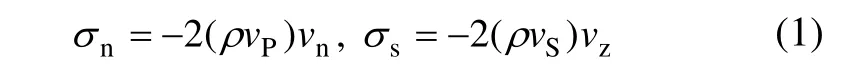
式中:σn为正应力;σs为剪应力;ρ为介质密度;vP为介质的P波速度;vS为介质的S波速度;vn为垂直方向质点速度;vz为水平方向质点速度。
边坡底部所受垂直向上剪切应力波方程为:
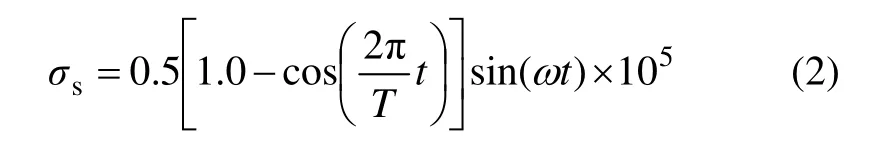
式中:T为地震波周期;t为地震波传播时间;ω为角频率。
1.3 网格划分
根据Kuhlemeyer等的研究,网格剖分的尺寸受输入波最短波长控制。设网格最大尺寸为Δl,输入波最短波长为λ,则Δl必须小于最短波长λ的1/10~1/8,地震波在边坡中传播速度为:
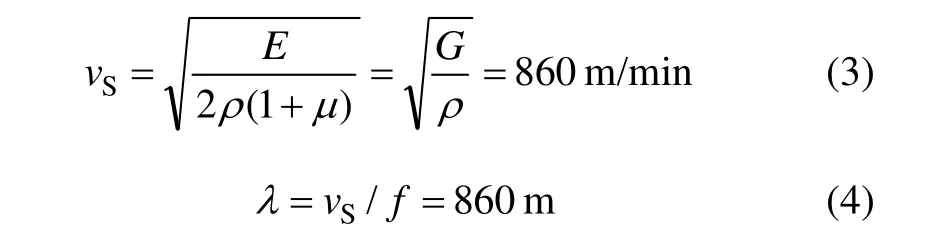
式中:λ为波长; f为应力波频率;E为介质弹性模量;G为介质剪切模量。
频率愈小,则波长越长,该处采用最小频率1 Hz计算波长,保证网格划分满足各种计算条件。网格剖分的尺寸Δl为:
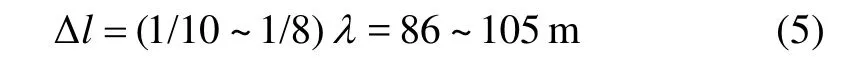
模型单元尺寸为10 m,远小于该Δl,满足进行动力学分析的要求。
1.4 动力持时的确定
动力响应计算的持续时间对边坡响应的影响体现在波动传播过程中。对于尺寸较大的边坡,若动力响应的计算持续时间太短,则波动未能传播到边坡顶部,边坡内部波场分布没有达到稳定,这时得到的边坡动力响应规律就不能真正反映边坡的动力响应规律。因此,动力输入的持续时间必须保证边坡内部的波场趋于稳定,才能提取波动过程中位移、速度、加速度的峰值,所得边坡动力响应分布才能反映边坡的动力响应规律,根据地震波在边坡中传播的速度确定动力响应持续时间为 4 s。
1.5 数值模拟工况
为分析影响边坡动力响应的因素,分别研究高度为210,380和600 m的边坡,并对不同高度的边坡分别施加频率为1,2,3,5和7 Hz剪切应力波。
2 边坡动力响应规律
2.1 边坡动力响应的监测
边坡在动力载荷作用下,坡体内部每个点的位移、应力、速度和加速度均在变化,如果只看某一个时刻的状态就不能全面反映边坡在动力载荷作用下的响应。由于事先并不知道在哪一时刻边坡受到的破坏最严重,当动力分析结束后再查看边坡的动力响应对于真实地了解边坡的动力响应意义不大。本文编制了fish程序,将动载荷作用下边坡体内所有节点的速度最大幅值记录下来,通过所有节点的位移和速度最大幅值可以看出边坡体的动力响应情况。记录边坡体所有节点的最大速度流程如图2所示。
2.2 地震波频率与坡体的放大作用
在地震波作用下,边坡体一些部位的位移、加速度等与其他部位的相比存在放大现象。祁生文[7]将这种放大作用用地震动力响应系数来表示。将边坡中的地震动力响应系数定义为边坡地震动力响应速度波动峰值与边坡脚速度峰值的比值[7]。边坡脚的速度和加速度等本身也存在放大现象,选用边坡脚的速度和加速度等作为参考量,边坡的地震动力系数就不能全面反映边坡的动力响应规律。本文将边坡的地震动力响应系数定义为边坡地震动力响应速度波动峰值与边坡底部速度波动峰值的比值。
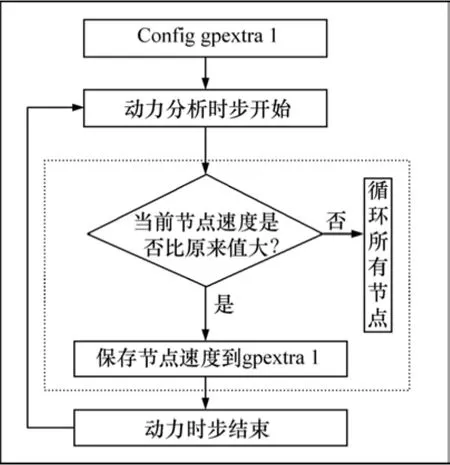
图2 记录边坡节点最大速度流程图Fig.2 Procedure of recording max velocity of all gridpoint
假定坡体内任意一点A的动力响应的速度峰值为vA,max,边坡底部B点的动力响应的速度峰值为vB,max,则A点的速度放大系数。这样,速度放大系数的分布规律便可以代表地震波作用下边坡体内速度的分布规律。为了研究整个边坡各个部位动力响应规律,通过图2所示过程,提取并保存边坡所有节点在整个计算时程中的速度峰值,在此基础上绘制了边坡动力响应速度放大系数等值线图。
图3所示为高度为380 m的边坡底部受到频率分别为1,3,5和7 Hz地震波作用下的动力响应系数等值线。不同频率地震波作用下动力响应系数极值列于表1。
地震波频率不同,应力波波长将不同,不同波长应力波传播到边坡顶部时,其反射波的特征也不一样,入射波和反射波的相互干涉也会不同。动力响应系数在边坡体内的分布也相应受到地震波频率的影响。
由图3(a)可见:该边坡在频率为1 Hz地震波作用下,绝大部分区域出现地震动力响应系数小于1的现象;在坡面及附近部分没有出现放大现象;在该频率地震波作用下,边坡体稳定性基本上没有受到影响。
由图3(b)可见:该边坡在频率为3 Hz的地震波作用下,边坡体的2个水平近地表部分区域出现了放大效应,边坡底部水平近地表部分放大现象没有边坡顶部放大现象明显;在坡面及附近部分没有出现放大现象;在该频率地震波作用下,边坡体稳定性基本上没有受到影响。
由图3(c)可见:该边坡在频率为5 Hz的地震波作用下,边坡体的2个水平近地表部分区域均出现了放大效应,边坡顶部水平近地表部分和边坡底部的放大程度接近;边坡中部出现放大现象,地震动力响应系数为1.1;在该频率地震波作用下,边坡体的稳定性基本上没有受到影响。
由图3(d)可见:该边坡在频率为7 Hz的地震波作用下,边坡体顶部水平近地表部分区域均出现了放大效应,边坡底部水平近地表部分没有出现地震动力响应系数放大现象;在该频率地震波作用下,边坡体的稳定性基本上没有受到影响。
在图3(a),(b)和(d)所示的3个边坡中,边坡面附近均没有出现边坡地震动力响应系数放大现象。

图3 不同频率地震波作用下的动力响应系数等值线Fig.3 Contour of seismic dynamic response coefficient with different frequency seismic waves
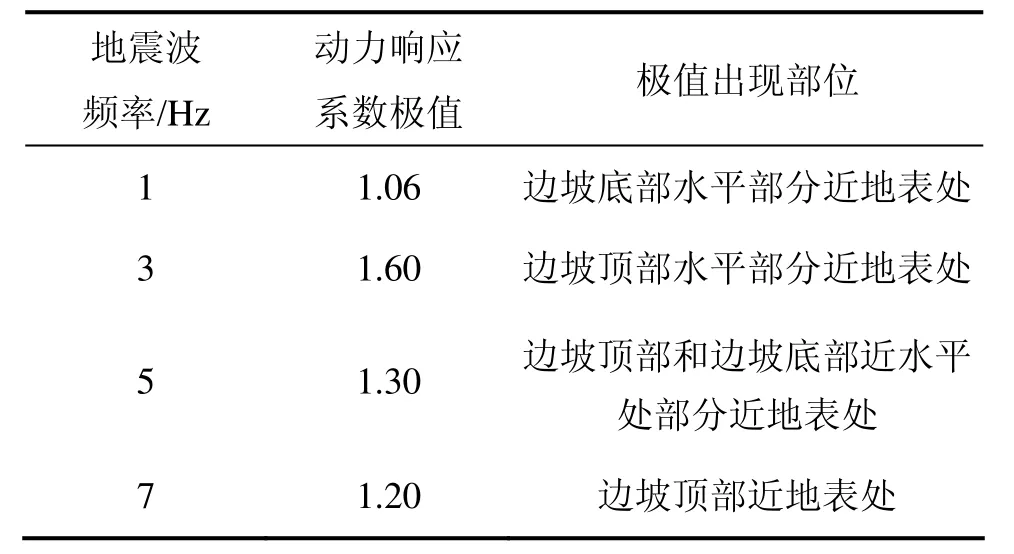
表1 不同频率地震波作用下动力响应系数极值Table1 Maximum seismic dynamic response coefficient with different frequency seismic waves

表2 不同边坡高度下动力响应系数极值Table2 Maximum seismic dynamic response coefficient with different height slopes
2.3 坡体高度与坡体的放大作用
边坡高度对边坡地震动力响应系数的分布规律也有一定影响。边坡高度增大,岩石边坡的自振频率降低,自振周期延长。对于在竖直地震荷载作用下的高岩石边坡,高度的变化对岩石边坡地震动力系数的影响较大。
在频率为1 Hz的地震波作用下,边坡高度不同,相同频率地震波在边坡体内传播并相互干涉的位置也会不同。
图4所示是不同频率地震波作用下的动力响应系数等值线。不同边坡高度下动力响应系数极值列于表2。由图4(a)可见:对于高度为210 m的边坡,其边坡底部近地表部分有放大现象;绝大部分区域出现地震动力响应系数小于1的现象;坡面及附近部分没有出现放大现象;该频率地震波作用下,边坡体稳定性基本上没有受到影响。
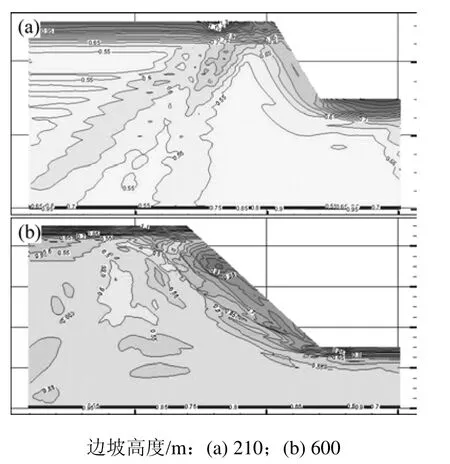
图4 不同边坡高度下动力响应系数等值线Fig.4 Contour of seismic dynamic response coefficient with different height slopes
由图4(b)可见:对于高度为600 m的边坡,边坡顶部近地表部分没有放大现象;绝大部分区域出现地震动力响应系数小于1的现象;坡面及附近部分没有出现放大现象;在该频率地震波作用下,边坡体稳定性基本上没有受到影响。
2.4 影响动力响应系数分布的原因
地震波垂直入射到地质界面时会发生反射,入射波还会与反射波发生干涉。那么,在反射界面附近会出现震动响应比其他地方放大的现象。
入射波的方程为:

式中:A1为振幅。
反射波的方程为:

图5 入射波和反射波坐标示意图Fig.5 Coordinate system of incident and reflect wave
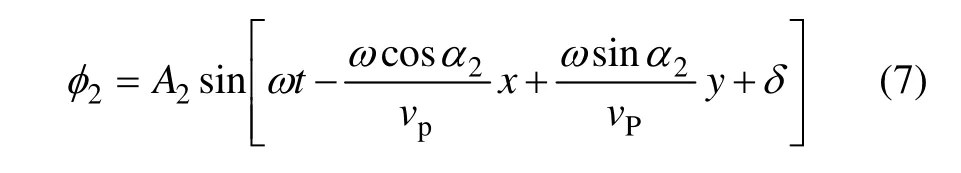
式中:δ为反射波与入射波的相位差,这里取值为π。
根据波的叠加原理,入射波和反射波叠加后的方程为:
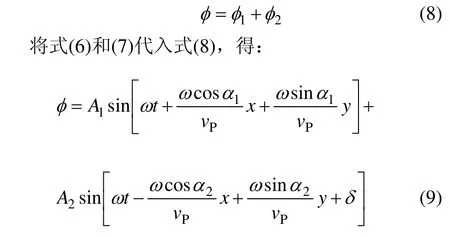
对于均质边坡来说,A1与A2相等,即入射地震波经边坡面反射后波的振幅没有发生改变。入射波和反射波叠加发生放大,就要求1φ和2φ必须同时为正才可以。否则,入射波和反射波叠加后就会发生振幅减小。
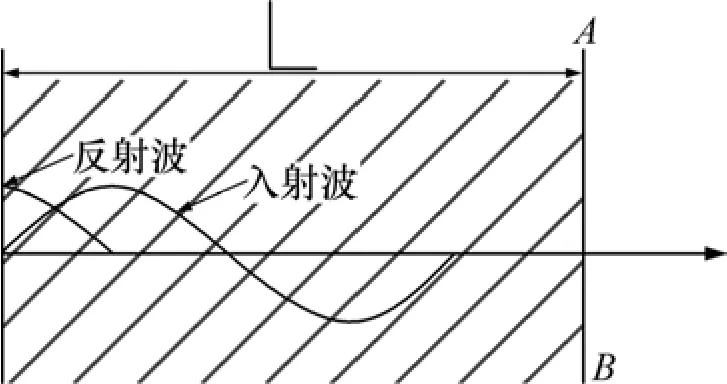
图6 入射波和反射波可能发生叠加的区域Fig.6 Superposition region of incident and reflect wave
图 6所示为入射波和反射波可能发生叠加的区域。图7所示为边坡体内会叠加的区域。
入射波到达边坡界面时发生反射,当入射波没有消失且反射波传播的距离没有超出一定范围时,入射波和反射波就会发生干涉,如图6中阴影部分所示。当向左传播的入射波和向右传播的反射波全部通过AB面时,入射波和反射波就不可能发生干涉现象。所以,边坡体内地震动力响应系数等值线图在边坡近地表部分存在放大现象。
根据以上分析,边坡体内可能发生干涉的区域如图7中阴影部分所示。从图7可见:在该阴影部分入射波和反射波才具有干涉的条件;超出该区域,虽然有反射波存在,但入射波已经传播完毕,即不存在入射波,故该区域不会再出现干涉现象。
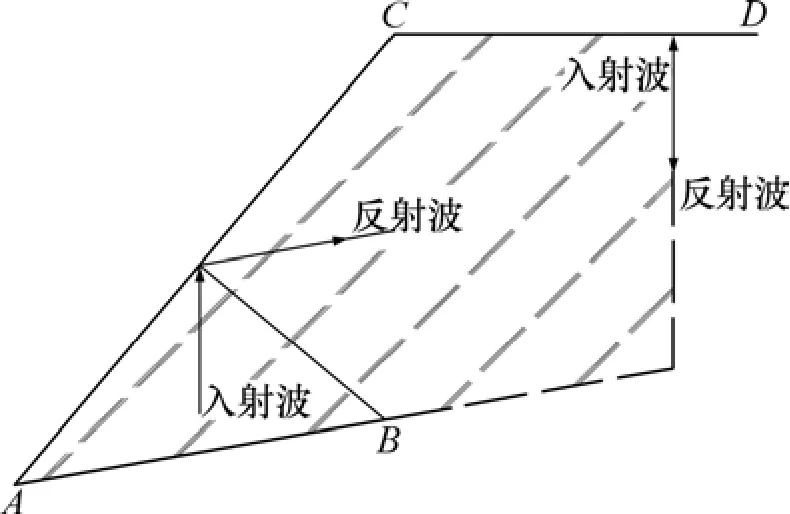
图7 边坡体内会叠加的区域Fig.7 Superposition region in slope
3 结论
(1) 记录边坡在动力波作用下的各物理量最大值能够更全面地了解边坡的动力响应规律,更真实地反映震波作用下边坡的动力响应规律。
(2) 边坡底部是地震波入射面,该位置没有放大现象,用该位置一点的速度作为基准值,能够更准确地反映边坡的动力响应规律。
(3) 边坡在动力作用下,动力放大现象出现的位置与边坡的形状、岩土体性质及地震波的特性等因素有关。边坡岩土体性质和地震波特性不同会导致最终边坡体内传播的地震波波长和波速等发生变化,在边坡的近地表部分发生放大现象的范围就会发生变化。边坡形状发生变化,地震波经过边坡面反射后在边坡内部发生干涉的位置也发生变化。
(4) 边坡在地震波作用下出现放大现象的区域主要集中在边坡近地表区域,该现象是入射地震波与反射地震波叠加的结果。边坡表面是曲面,不同位置反射波传播方向不同,为边坡体内部出现放大现象提供了条件。
[1] 李海波, 蒋会军, 赵坚, 等. 动荷载作用下岩体工程安全的几个问题[J]. 岩石力学与工程学报, 2003, 22(1): 1887-1891.
LI Hai-bo, JIANG Hui-jun, ZHAO Jian, et al. Some problems about safety analysis of rock engineering under dynamic load[J].Chinese Journal of Rock Mechanics and Engineering, 2003,22(1): 1887-1891.
[2] 刘汉龙, 费康, 高玉峰. 边坡地震稳定时程分析方法[J]. 岩土力学, 2003, 24(4): 553-556.
LIU Han-long, FEI Kang, GAO Yu-feng. Time history analysis method of slope seismic stability[J]. Rock and Soil Mechanics,2003, 24(4): 553-556.
[3] LIN Meei-ling, WANG Kuo-lung. Seismic slope behavior in a large-scale shaking table model test[J]. Engineering Geology,2006, 86(2): 118-133.
[4] 唐洪祥, 邵龙潭. 地震动力作用下有限元土石坝边坡稳定分析[J]. 岩石力学与工程学报, 2004, 23(8): 1318-1324.
TANG Hong-xiang, SHAO long-tan. Finite element analysis on slope stability of earth-rock dam under earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8):1318-1324.
[5] 周永江, 王开云, 符文熹, 等. 高地震烈度区堆积体边坡动力响应时程特征分析[J]. 山地学报, 2007, 25(1): 93-98.
ZHOU Yong-jiang, WANG Kai-yun, FU Wen-xi, et al. Analysis on time history dynamic response of a rock fall-type slope under high earthquake intensity[J]. Journal of Mountain Science, 2007,25(1): 93-98.
[6] 何蕴龙. 岩质边坡施工爆破振动速度近似计算方法[J]. 岩石力学与工程学报, 1996, 15(1): 19-25.
HE Yun-long. An approximate calculation method for the accelerations in the rock slope under blasting construction[J].Chinese Journal of Rock Mechanics and Engineering, 1996,15(1): 19-25.
[7] 祁生文. 单面边坡的两种动力反应形式及其临界高度[J]. 地球物理学报, 2006, 49(2): 518-523.
QI Sheng-wen. Two patterns of dynamic responses of single-free-surface slopes and their threshold height[J]. Chinese Journal of Geophysics, 2006, 49(2): 518-523.
[8] 秋仁东, 石玉成, 付长华. 高边坡在水平动荷载作用下的动力响应规律研究[J]. 世界地震工程, 2007, 23(2): 131-138.
QIU Ren-dong, SHI Yu-cheng, FU Chang-hua. General laws of dynamic responses of the high slopes under horizontal dynamic input[J]. World Earthquake Engineering, 2007, 23(2): 131-138.
[9] 徐光兴, 姚令侃, 李朝红. 边坡地震动力响应规律及地震动参数影响研究[J]. 岩土工程学报, 2008, 30(6): 918-923.
XU Guang-xing, YAO Ling-kan, LI Zhao-hong, et al. Dynamic response of slopes under earthquake and influence of ground motion parameters[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(6): 918-923.
[10] 陈玲玲, 陈敏中, 钱胜国. 岩质陡高边坡地震动力稳定分析[J]. 长江科学院院报, 2004, 21(1): 33-35.
CHEN Ling-ling, CHEN Min-zhong, QIAN Sheng-guo.Stability analysis of high steep rocky slope under earthquake loads[J].Journal of Yangtze River Scientific Research Institute, 2004,21(1): 33-35.
[11] Gazetas G. Seismic response of earth dams some recent developments[J]. International Journal of Soil Dynamics and Earthquake Engineering, 1987, 6(1): 2-47.
