航空主发电机定子三维温度场的有限元分析

夏佳青，刘荣林，丁晓宇

（中国民航大学航空自动化学院，天津 300300）

航空主发电机定子三维温度场的有限元分析

夏佳青，刘荣林，丁晓宇

（中国民航大学航空自动化学院，天津 300300）

航空发电机的体积小，电磁负荷高，发热问题更显重要。温度场计算是研究发电机发热的主要手段。以B747发电机为研究对象，介绍了主发电机的发热热源、不同部件的导热系数和各散热面的散热系数，建立了航空主发电机定子三维温度场计算的数学模型，利用ANSYS有限元软件对温度场进行求解，得到定子温度场分布，找出电机最高发热部位，并分析了电机的相关因素变化对电机温度场分布的影响，得出了一些有益的结论，并用实例验证了结论的正确性。

航空发电机；温度场；ANSYS

发电机是飞机上的重要部件之一，随着飞机电控程度的日益提高，装机总容量和单机容量越来越大。近年来，在发电机的维修中发现，某些大型客机的交流发电机发热问题严重，大型飞机交流发电机与地面普通发电机的结构、电磁负荷以及工作条件差异很大，发热及老化机理尚不十分明确，致使工程维修无法进行的现象时有发生，因此研究发电机发热问题具有实际的意义。

温度场计算是研究发电机发热的主要手段。三级式航空交流发电机的永磁机和励磁机的发热较少，可不必考虑。因此热计算的任务就是要计算主发电机的温升。

国内外对电机温度场分布的计算，主要集中在大型水轮发电机和汽轮发电机中[1-14]，航空发电机的温度场分析与计算也有些报导[15]。有限单元法具有剖分灵活、算法通用，同时方便在计算机中计算的优点，因此现在被普遍应用于电机电磁场和温度场的计算。

本文在分析目前主流飞机机型所配备的三级式无刷交流发电机主发电机热源的基础上，用有限元法建立主发电机定子三维温度场的数学模型，并用ANSYS软件对不同工况下的定子温度场求解，找出电机最高发热部位，讨论了不同绝缘等级、通风槽风速对电机温度分布的影响，得出一些有用的结论。为以后深入研究电机的发热问题提供一个比较实用的方法。

1 温度场计算的相关参数

1.1 主发电机发热源的求取

发电机在能量变化过程中一定会产生各种损耗，这些损耗大多会变成热量，使电机的温度升高。损耗从产生的部位可划分为铁心损耗pFe、绕组损耗pCu和机械损耗pZ。

主发电机的结构为旋转磁极式，其绕组为直流供电，所以没有转子铁损耗，是一个具有定子铁心损耗pFe1、定子绕组铜损耗pCu1和转子绕组铜损耗pCu2的3个主要热源。这些损耗的计算可通过文献[16]方法来获得。获得这些损耗后，将其转换成单位体积生热率。

1.2 等效导热系数

航空发电机主发电机绕组为双层绕组，把整个定子槽做等效导热处理，对定子槽做如下假设：①浸渍漆均匀地填充在槽内；②铜导线上的绝缘漆均匀分布；③定子铁心和槽绝缘紧密地粘结在一起；④定子槽内的铜线温度变化忽略不计。

在以上假定的条件下，可以分别将上、下层槽内的铜线近似地看作一个导热体，为整铜块；槽绝缘、铜线的漆膜和浸渍漆等效为另外一个导热体，等效之后的铜块位于槽的中心，四周与壁面平行，槽绝缘、浸渍漆在铜线周围均匀地分布。各种绝缘材料的导热系数等效之后可按照下式计算

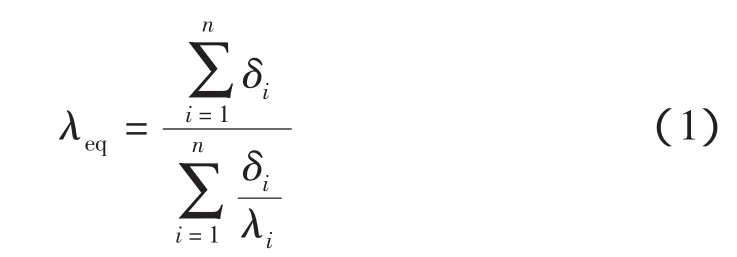
式中：λeq为导热系数的等效值；δi（i=1，2，…，n）为各导热体的厚度；λi为各导热体的导热系数。

1.3 散热系数的确定

对流传热是非常复杂的物理过程，其强度不仅取决于流体运动速度、运动性质和固体表面的形状，还取决于流体的物理性质。流体与固体壁面间的对流换热，可用下式表示

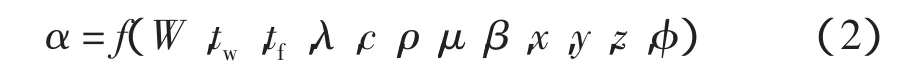
式中：W 为流体的速度（m/s）；tw为壁面温度（℃）；β为流体的体积膨胀系数；λ、c、ρ分别为流体的导热系数、比热容、密度；tf为流体的温度（℃）；μ为流体的粘度（m2/s）；x、y、z为直角坐标的尺寸；φ 为固体壁面的形状。

对流散热系数是一个与很多变量有关的函数，一般在实际计算中采用经验公式来计算[8]：

1）定子铁心内圆的散热系数（W/（cm2·℃））

式中：vn为转子周速（m/s）。

2）定子铁心外圆的散热系数（W/（cm2·℃））

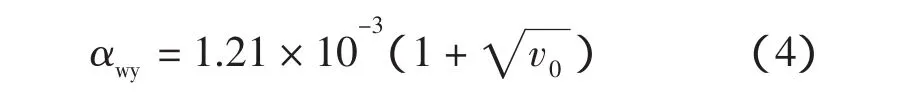
式中：v0为定子铁心外圆处风速（m/s）。

3）通风沟内绕组表面的散热系数（W/（cm2·℃））

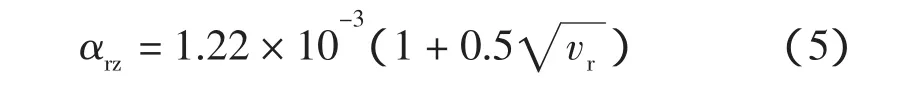
式中：vr为绕组表面风速（m/s）。

4）通风沟内铁心表面的散热系数（W/（cm2·℃））

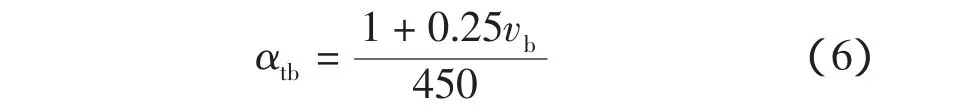
式中：vb为通风沟内风速（m/s）。

2 主发电机定子三维温度场的计算模型

2.1 假定条件

本文所研究的航空发电机采用径向强迫通风，由于电机结构和风路的复杂性，从而做以下假设[16]：

1）假设处于一个定子槽内的上、下层绕组发热状态是相同的；

2）考虑定子绕组铜耗时，忽略径向磁通损耗；

3）假设槽内所有绝缘的热性能和主绝缘都相同，铜导线的绝缘漆均匀分布；

4）通风沟中齿和轭的表面、槽绝缘的外表面及轭背部与空气接触面的散热系数分别取其平均值；

5）认为定子径向通风沟内流体的物理参数变化对定子温度场的影响较小，可忽略不计，通风沟内气体温度沿径向呈线性分布。

2.2 求解域

根据电机结构和风路的对称性，可以认为定子每个槽都有相同的热源以及相同的散热边界，定子铁心的最热段应处在定子铁心中部，因此可将定子三维温度场求解区域确定为轴向半个铁心段、周向半个齿距、径向从铁心内圆到铁心外圆的范围，求解区域如图1所示，图中不同深浅的颜色代表不同的材料实体，x、y、z分别为周向、径向、轴向。

由图1可得，定子温度场定解问题为

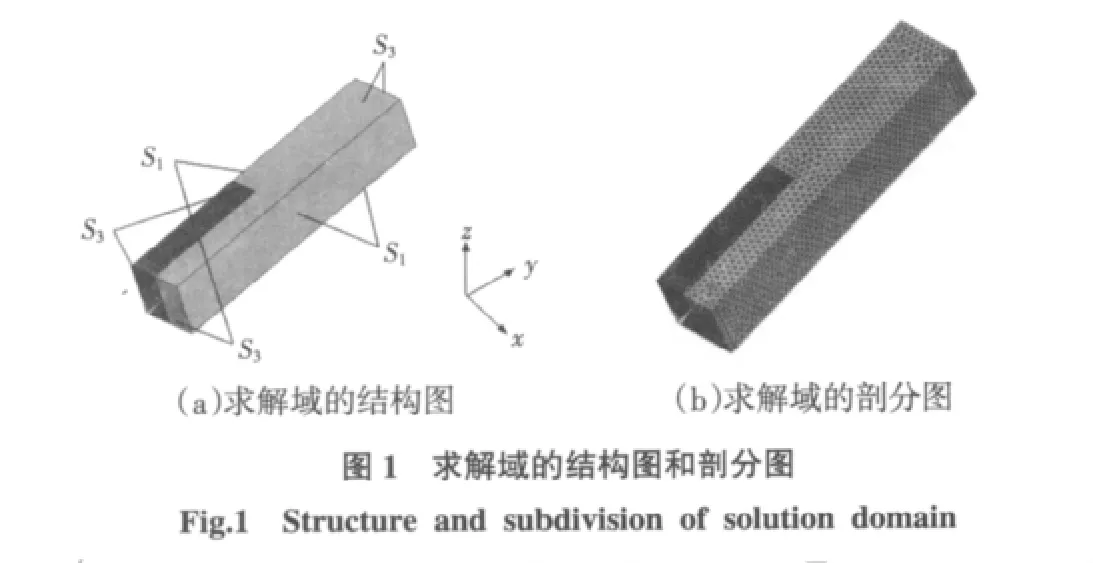
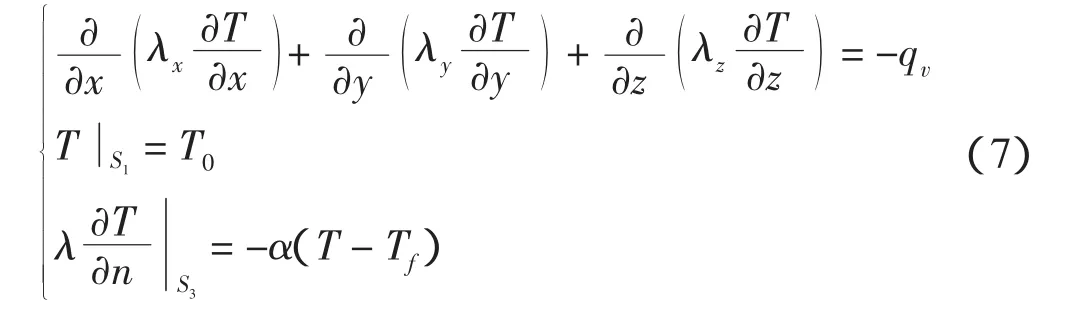
式中：T 为物体温度（℃）；λx、λy、λz分别为 x、y、z方向的导热系数（W/（mm·℃））；qv为热源密度（W/mm3）；边界面S由第1类边界S1和第3类边界S3两部分组成；T0为S1面周围的温度；α为S3面的散热系数（W/（mm·℃））；Tf为S3面周围介质温度。根据变分原理，上述混合边值问题可以转变为相应的泛函和条件变分问题

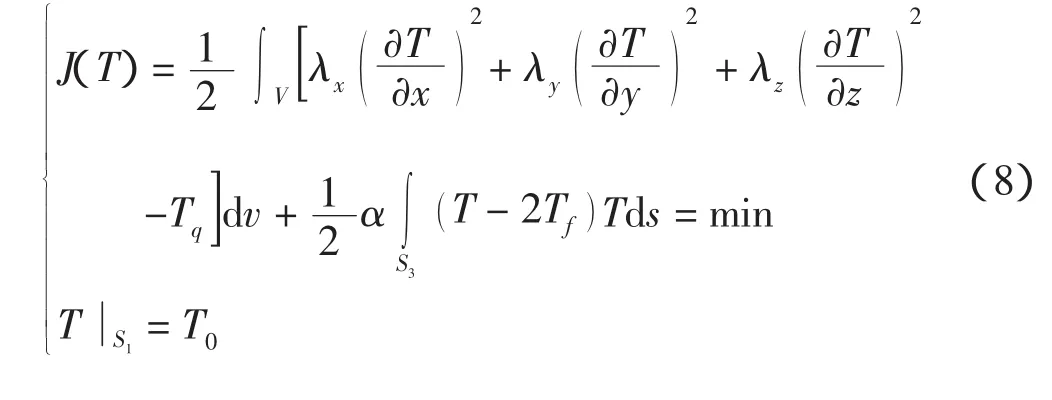
3 计算结果及分析

3.1 不同工况下定子温度场分布

通过ANSYS软件分析得到电机在两种工况下的定子三维温度场分布，如图2所示。图2（a）、（b）分别为：工况1额定负载即三相平均电流值为167 A，工况2为三相平均电流为120 A。

图2中定子的上端为出风口端，下端为进风口端，从图2中可以看出定子最高温度出现于绕组的下层绕组上，两种工况下最高温度分别为119.2℃和88.3℃。电机的最高温度之所以会出现在下层绕组上有以下几个主要原因：①电机运行过程中的主要热源为定子绕组；②绕组中的损耗有基本铜耗、环流损耗和涡流损耗，其值较大；③下层绕组的部分热量通过铁心和上层绕组向外散热，部分通过导热性能不太好的气隙传热。从总体来看，下层绕组的散热条件还比较差。

下面以主发电机额定负载状态下温度场的计算结果为研究对象，本文将从径向和轴向两个方面来分析定子铁心温度的变化。图3为定子铁心表面上的一点在径向的温度分布，从中可以看出由于冷却气体沿径向吸收热量，温度增加，从而使定子铁心的温度沿径向不断增加。图4为定子齿中心段面的一点在轴向的温度变化，由于电机采用径向通风方式，定子铁心的最热段应处在定子铁心的中部，所以该曲线基本反映了温度的变化。

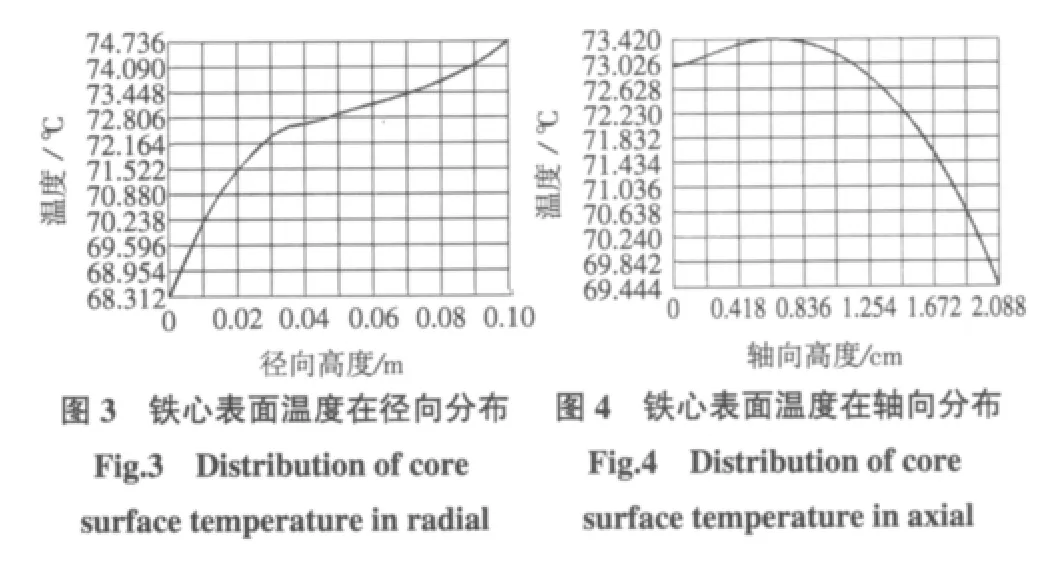
图5为下层绕组中的一点在径向的温度分布。由于电机采用径向通风方式，冷却气体沿径向温度不断增加和散热同时作用，从而使绕组最高温度点出现在距出风口一段距离的地方。图6为下层绕组中的一点在轴向上的温度分布，从图4可知定子铁心表面温度变化范围为69.4～73.4℃，最大温差为4℃；由图6可知定子绕组的温度从117.5℃变化到119.17℃，变化范围为1.67℃。可见径向高度不同，定子温度在轴向上温度变化也不同，这与热源的存在和通风冷却系统有密切关系。

为了对定子温度场进行研究，特意将主发电机定子不同部位的温度用表格的形式列举出来，如表1所示。定子绕组的温度分布较均匀，铁心与温度较高的热源和温度较低的冷却气体同时相接触，所以温度变化范围比较大。从总体上看，电机温度的最高点位于下层绕组距出风口一段距离的位置，温度最低点位于通风沟进风口附近的铁心上。

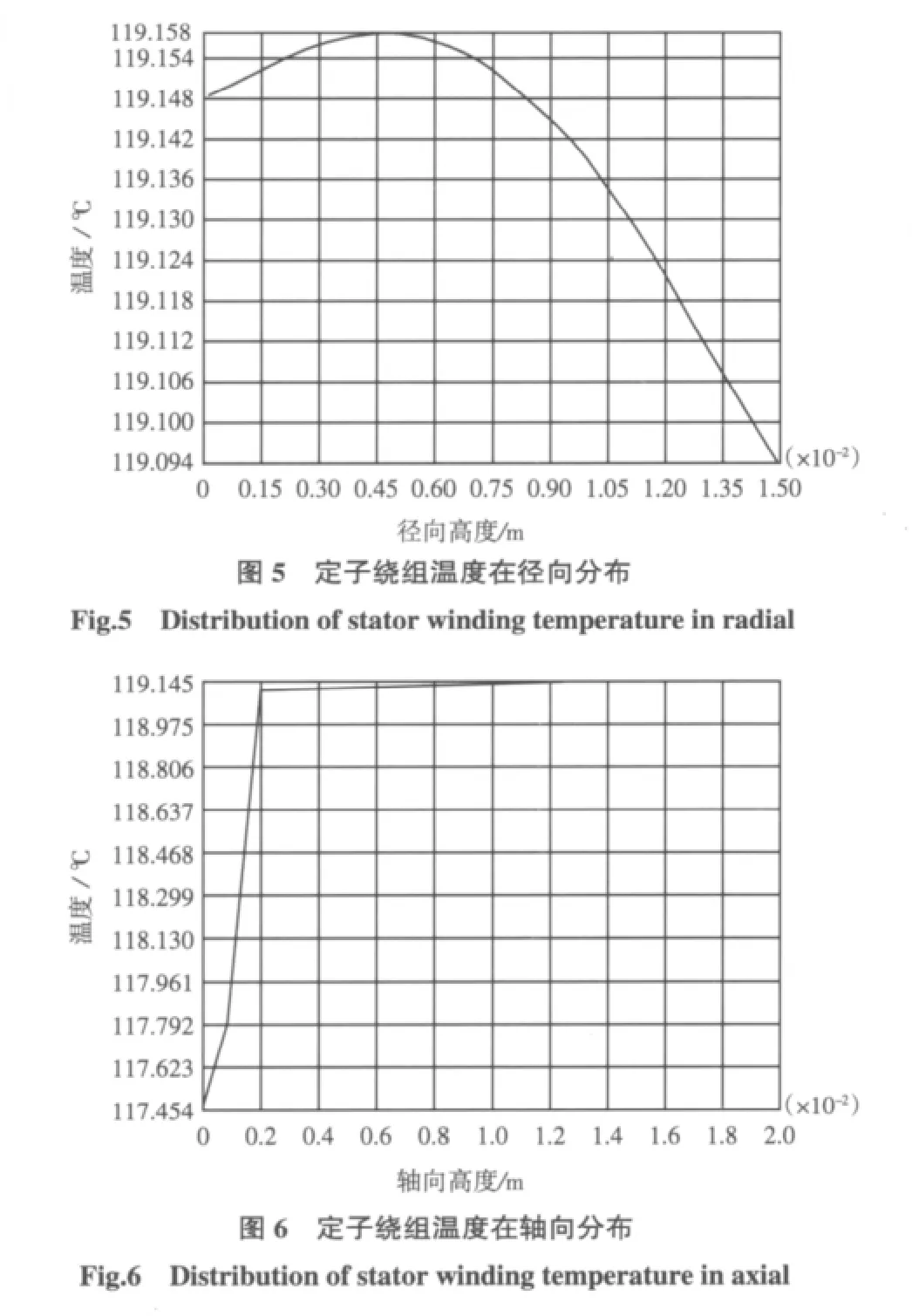
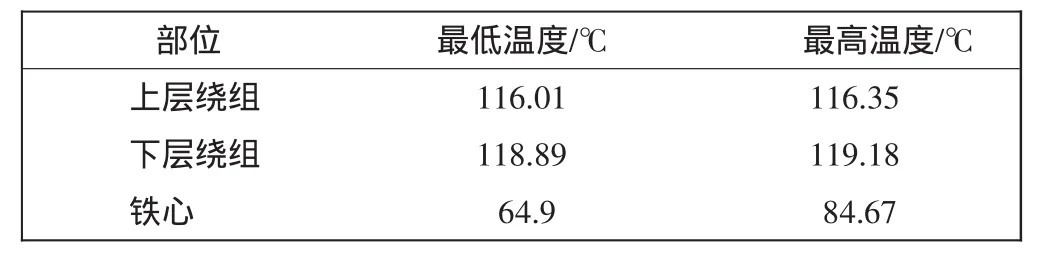
表1 计算结果数值分析Tab.1 Results of numerical analysis

3.2 绝缘材料对主发电机定子温度场的影响

绝缘材料导热性能的好坏对绕组温升的影响是不能被忽略的。不同级别的绝缘材料具有不同的导热系数。

A级绝缘材料λA≈0.1 W/（m·k）；B级绝缘材料λB≈0.16 W/（m·k）；F级绝缘材料λF≈0.26 W/（m·k）。为了研究3种级别的绝缘材料对电机温度场分布的影响，将A级、B级、F级绝缘材料条件下电机额定负载情况下的定子温度场分别进行计算，分布如图7所示。

表2为计算后得到的数据，从表2和图7中3种绝缘级别条件下绕组和铁心的温度情况可知，因为A级、B级绝缘比F级绝缘的导热性能差，所以前两者电机绕组的最高温度都明显高于后者电机绕组的温度，而且这种在理论分析情况下所计算出来的A、B级绝缘的绕组最高温度都明显超过各自绝缘材料所能承受的温度，势必会造成绝缘材料的损坏，可见，电机绝缘材料导热性能的好坏对定子绕组的温升影响较大，A、B级绝缘材料均不能用于航空主发电机的绕组绝缘。同时，从表2中可以看出，A、B、F级绝缘下电机定子铁心总体的温升变化不大，这主要是因为电机绕组损耗产生的总热量不变，所以绝缘材料导热性能的好坏对电机铁心温升的影响较小。

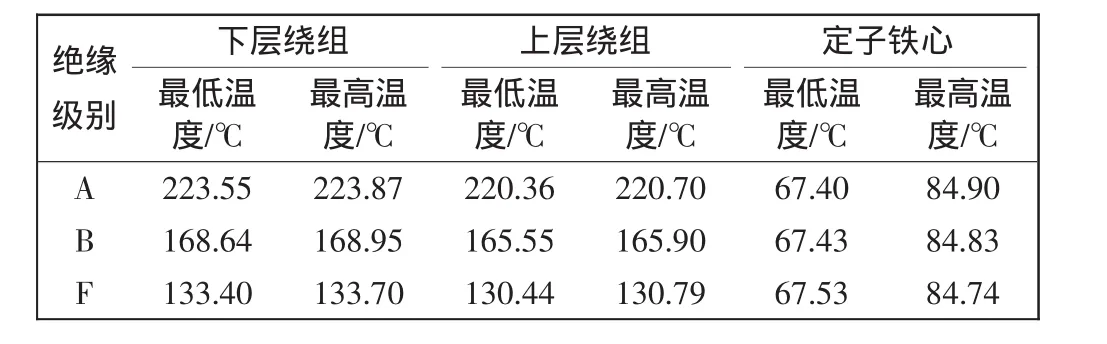
表2 不同绝缘级别时的计算结果Tab.2 Results by calculated in different level insulation

电机绕组的温升和温度场分布与电机绝缘材料导热性能的好坏有着密切的联系，铁心的温升和温度分布也与绝缘材料导热性能有着一定的联系，同时导热性能好坏对电机的总体温度分布也有一定影响。因此，在实际工程计算中要准确地计算绝缘材料的导热系数。

3.3 通风沟风速对主发电机定子温度场的影响

表3为电机定子绕组、铁心温度在定子通风槽处于不同风速时的计算结果。

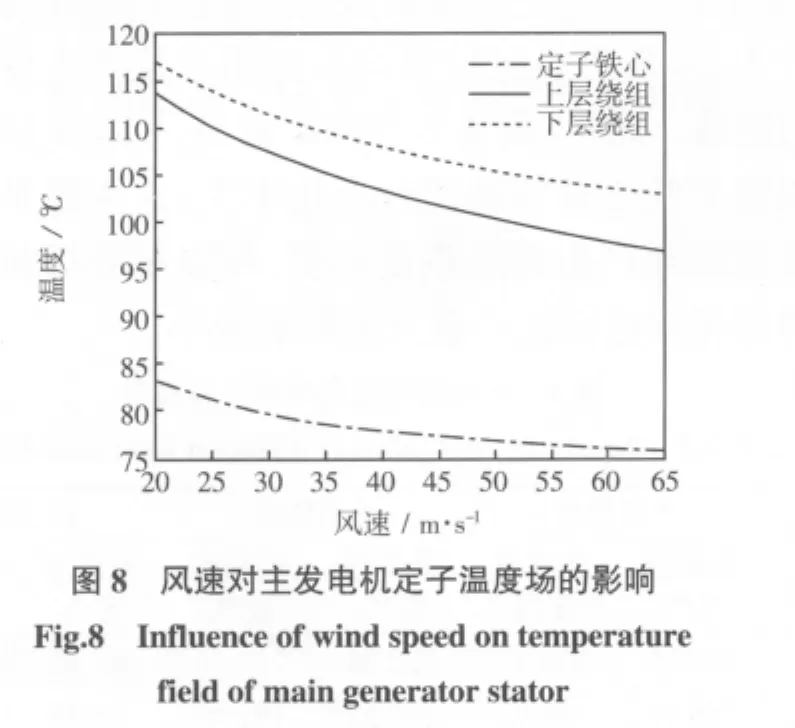
由表3可以看出，当电机风速增大时，电机铁心和定子绕组的最高温度与最低温度都有所降低，而且温度分布也发生了变化。图8为主发电机定子铁心和上下层绕组最高温度在风速变化时做出的曲线。从图8中可以看出当风速增加到一定程度时，曲率明显变小。从实际工程角度出发，当冷却风速较小时，增加风速，电机温度下降十分明显。当风速增加到一定程度时，再增加风速对电机温度的影响比较小。从而可知电机冷却风速的恰当选择对于电机寿命和效率的提高有着显著的作用。

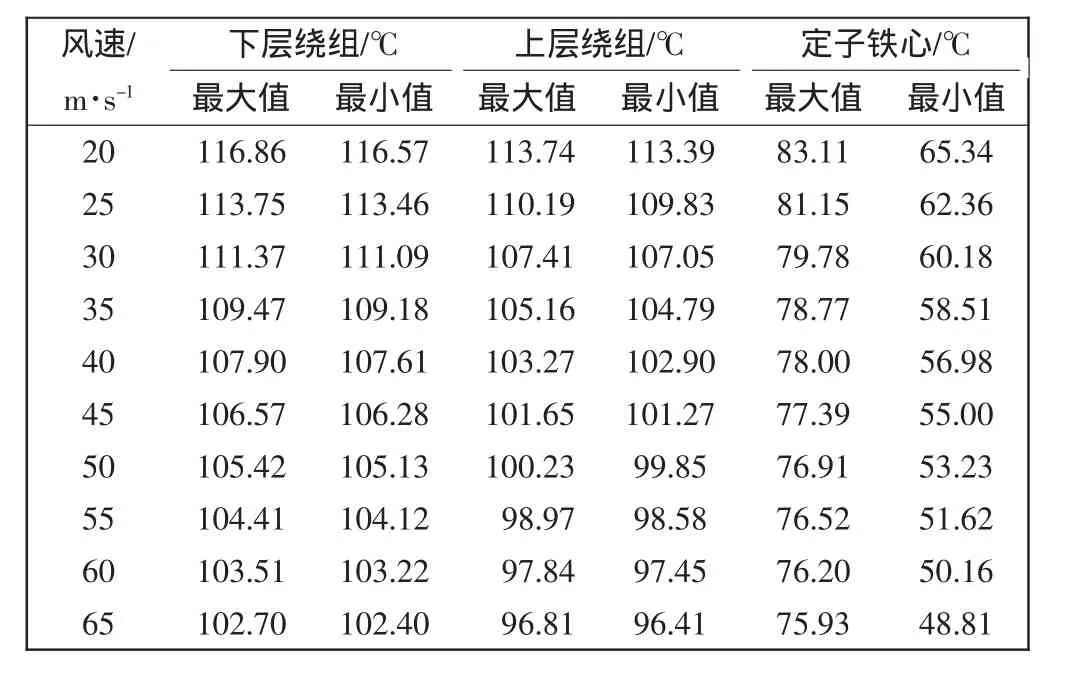
表3 通风槽不同风速时的计算结果Tab.3 Results by calculated in different wind speed of ventilation slots

4 结语

1）径向通风的电机冷却气体在流动的过程中会不断吸收热量，温度不断增加，从而使电机温度在径向上的分布变化较大。因此径向通风的电机在分析温度场时必须要考虑冷却气体的温度在径向的变化。

2）电机定子温度的最高点位于下层绕组离出风口一定距离的地方，温度的最低点位于离通风口很近的铁心上。

3）电机绕组温升和温度场分布与电机绝缘材料的导热性能好坏有着紧密联系，同时绝缘材料的导热性能好坏对电机温度场总体分布的影响也不容忽视。因此，在实际工程中应准确计算绝缘材料导热系数。

4）定子通风槽风速的大小会改变电机温度及温度分布，因此在实际工程中应该合理选择。

[1]MALIK E ELBULUK，DAVID KANKAM M.Potential starter/generator technologies for future aerospace applications[J].IEEE AES Systems Magazine，1997，36（4）：24-31.

[2] GERLANDEO A DI，PERINI R.Analytical Evaluation of the Stator Winding Temperature Field of Water-cooled Induction Motors for Pumping Driver[C]//ICEM2000，Helsinki University of Technology，Espoo，Finland，August，2000：130-134.

[3]GUREVICH E，OSHURKOV P.Determination of Rotor Winding Temperature of the Turbogenerator with the Brushless Excitation System[C]//ICEM 2000，Helsinki University of Technology，Espoo，Finland，August，2000：156-160.

[4] ARMOR A F，CHARI M V K.Heat Flow in the Stator Core of Large Turbine Generators by the Method of Three-Dimensional Finite Elements：PartⅠ：Analysis by Scaler Potential Formulation，PartⅡ：Temperature Distribution in the Stator Iron[C]//IEEE Trans on PAS，1976，95（5）：1648-1668.

[5]ANXO PRIETO ALONSO M，LÓPEZÁFERNÁDEZ X M，MANUELPÉREZ DONSIÓN.Harmonic Effects on Rise of A Squirrel Cage Induction Motor[C]//ICEM 2000，Helsinki University of Technology，Espoo，Finland，August，2000：144-147.

[6]KROK R，MIKSIWICZ R，MIZIA W.Modeling of Temperature Fields in Turbongenerator Rotors at Asymmertrical Load[C]//ICEM 2000，Helsinki University of Technology，Espoo，Finland，August，2000：1005-1009.

[7]栾 茹，傅德平.新型浸润式蒸发冷却电机定子三维温度场的研究[J].中国电机工程学报，2004，24（8）：206-209.

[8] 姚若萍，饶芳权.蒸发冷却水轮发电机定子温度场研究[J].中国电机工程学报，2003，23（6）：87-90.

[9] 李伟力，丁树业.基于耦合场的大型同步发电机定子温度场的数值计算[J].中国电机工程学报，2005，25（13）：129-134.

[10]侯云鹏，李伟力.绝缘老化对大型水轮发电机定子最热段段温度场的影响[J].大电机技术，2001（1）：17-22.

[11]李伟力，周 封.大型水轮发电机转子温度场的有限元计算及相关因素的分析[J].中国电机工程学报，2002，22（10）：85-90.

[12]李德基，白亚民，王绍禹.绝缘老化对定子温升的影响[J].大电机技术，1998（6）：25-33.

[13]颜威利.三维稳态温度场的有限元法[J].河北工业大学学报，1984（6）：8-13.

[14]方日杰，赖烈恩，蒋俊杰，等.用热网络法计算大型水轮发电机定子温度场[J].大电机技术，1989（1）：7-10.

[15]庄心复，陈厚志.循油冷却航空交流发电机三维温度场的网络拓扑法求解[J].航空学报，1989，10（3）：144-150.

[16]魏永田.电机内热交换[M].北京：机械工业出版社，1998.

Analysis of 3D Temperature Field of Aviation Main Generator Stator by Finite Element Method

XIA Jia-qing， LIU Rong-lin， DING Xiao-yu
（College of Aviation Automation，CAUC，Tianjin 300300，China）

The aviation generator is small in bulk and high in electromagnetic load， so the heating problem is especially serious.The calculation of the temperature field of generator is the main means analyzing the heat of generator.The paper take B747 AC generator as researched object， the source of heat， the thermal conductivity of generator components and the thermal coefficient of surface heat having introduced，the mathematical model of 3D temperature field of aviation main generator stator is derived.With the ANSYS software the temperature field is calculated，the distribution of temperature field is got and the hottest position of the generator is indicated.Then， some factors which influence the distribution of the temperature of stator are analyzed， and get some helpful conclusion.The accuracy of the conclusion is verified through an example.

avaiation generator； temperature field； ANSYS

V241.01

A

1674－5590（2011）01－0018－05

2010-09-25；

2010-11-05 基金项目：中国民航大学科研基金项目（08CAUC-E06）

夏佳青（1986—），男，安徽巢湖人，硕士研究生，研究方向为检测技术.

（责任编辑：王纪宽）