基于贝叶斯的航空备件需求研究与应用
2011-05-31陈凤腾左洪福
陈凤腾,左洪福
(1.徐州工程学院,江苏 徐州 221008;2.南京航空航天大学民航学院,南京 210016)
基于贝叶斯的航空备件需求研究与应用
陈凤腾1,左洪福2
(1.徐州工程学院,江苏 徐州 221008;2.南京航空航天大学民航学院,南京 210016)
鉴于目前航空备件需求计算应用泊松公式存在计算结果误差较大的问题,依据历史故障数据并应用广义更新过程建立反映历史故障数据以及维修能力的可靠性分布模型,同时针对目前历史故障数据主要是小样本事件,应用贝叶斯方法并采用切片采样法对可靠性分布模型进行参数估计。最后通过实例进行分析,结果表明实际故障次数和实际故障情况较为吻合,增大了模型的应用范围。
贝叶斯;航空备件;故障率;切片采样法
备件需求预测直接影响航空公司安全运营和成本管理,是维修活动的基础,是关系到航空公司信誉和效益的一个关键环节。航空备件需求和预测问题涉及了可靠性、维修性、航空保障以及系统安全等领域,成为国内外学者关注的课题之一[1-2]。
目前飞机制造商(如波音、空客等)向用户提供备件推荐数量的计算方法主要是齐次泊松公式[3]。该方法主要假设各种零部件的可靠性模型服从理想的指数分布,这在计算初始备件需求数量时具有方便、易于计算等特点,但未能充分反映实际设备故障特性,而且应用该方法要假设部件的修理和更换服从更新过程,这和实际情况脱节,其预测结果和实际需求偏差较大。
面对这些问题,文献[4]引进维修度并应用广义更新过程进行可靠性建模,不仅可以反映设备实际更换的特点,而且还可以反映设备维修能力以及修理后恢复的能力。
对于历史故障、寿命数据为大样本时,应用上述方法并通过似然函数进行参数估计,可以获得较高的精度。但由于目前使用年限以及管理能力、水平的限制,获得的历史故障数据往往是小样本,直接应用似然函数计算方法存在其计算精度较低的问题,为此,本文根据航空装备6种故障率特性,首先建立相应的故障分布模型,然后根据历史故障数据和先验知识,初步确定模型的分布和范围。由于使用年限和管理水平的限制,设备故障多为小样本事件,故本文选取适于处理小样本事件的贝叶斯方法,同时对于高维复杂的无法直接计算的数学公式应用切片采样法进行数值仿真,并将其应用到任意分布函数。为了反映同类设备历史故障和航空公司对该类设备的实际维修能力,本文借助广义更新过程进行可靠性建模。
1 广义更新过程
广义更新过程(GRP)首先被Kijima和Sumita提出并应用到复杂可修系统的分析[4-5],根据维修方式的不同将该系统分5种状态,同时引入表征维修能力的维修度(q)概念和其对应:修复如新(q=0)、修复如旧(q=1)、修复介于新旧之间(0
对于航空备件需求模型,对应不同维修策略,根据该类设备的故障特性建立起相应的故障分布模型,限于篇幅,本文主要对可靠性分布模型为Weibull进行计算说明。
2 极大似然法
当历史故障数据为大样本时,往往用极大似然法对分布模型进行参数估计,由Weibull分布函数和公式可求得第i(1≤i≤n)次的概率密度函数如式(1)和式(2)所示

在应用广义更新过程进行参数估计时存在以下两种情况:故障截尾和时间截尾。故障截尾表示既定故障次数出现之后即可结束故障事件统计,而时间截尾表示既定时间T到达之后即可结束统计。对于对这两种截尾进行参数估计主要通过如下两种似然函数计算[6-7]。
1)故障截尾的似然函数为
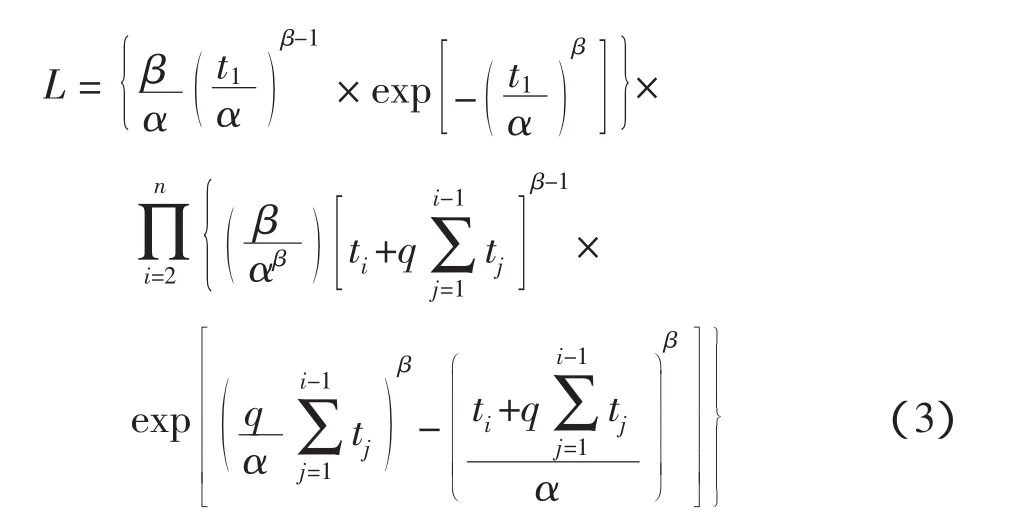
为了求q的参数估计值,现对ln L求参数q的偏导数,并令其为0,联立上面3个公式,应用拟牛顿迭代算法可得到参数估计值。
2)时间截尾的似然函数为
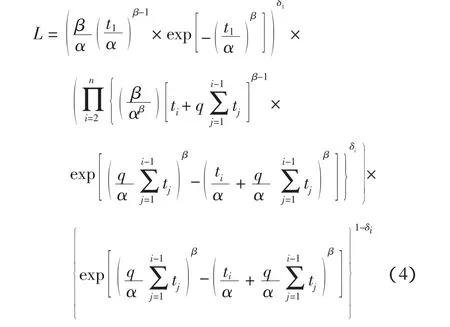
式中:δi表示截尾与否的变量,对q的参数估计方法同上。
当历史数据较多时,应用极大似然函数效果较好,对于小样本数据来说,其计算精度较低,而采用Bayes法基于先验知识,处理小样本精度较高。
3 Bayes法
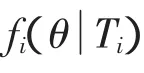
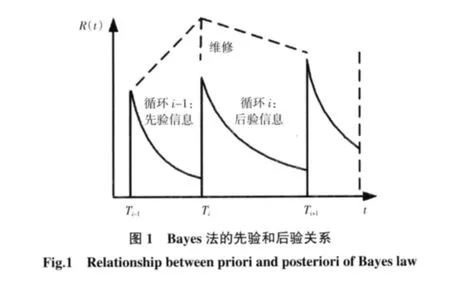
根据图1首次寿命周期概率密度分布如式(5)所示

其中:f(1θT1)是 θ的后验分布在周期1给定故障经历;L(T1θ)是似然函数。
式(7)求得的后验分布在第2次循环周期内则变成先验分布,具体如式(6)所示
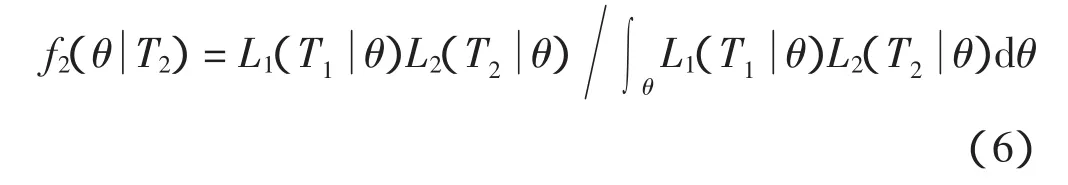
第n次循环的寿命周期内应用Bayes定理如式(7)所示
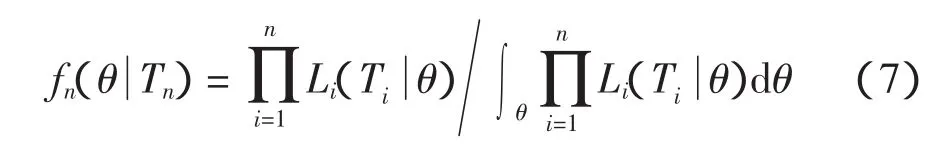
或展开如式(8)所示
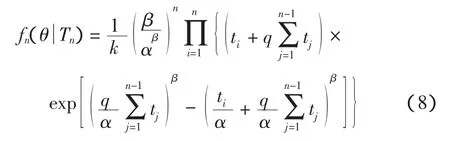
其中:n是故障次数;k是计算因子。具体如式(9)所示
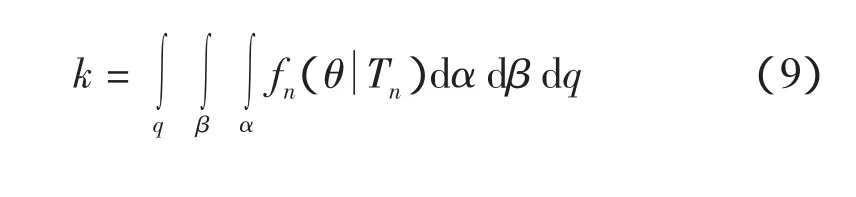
4 切片样本法
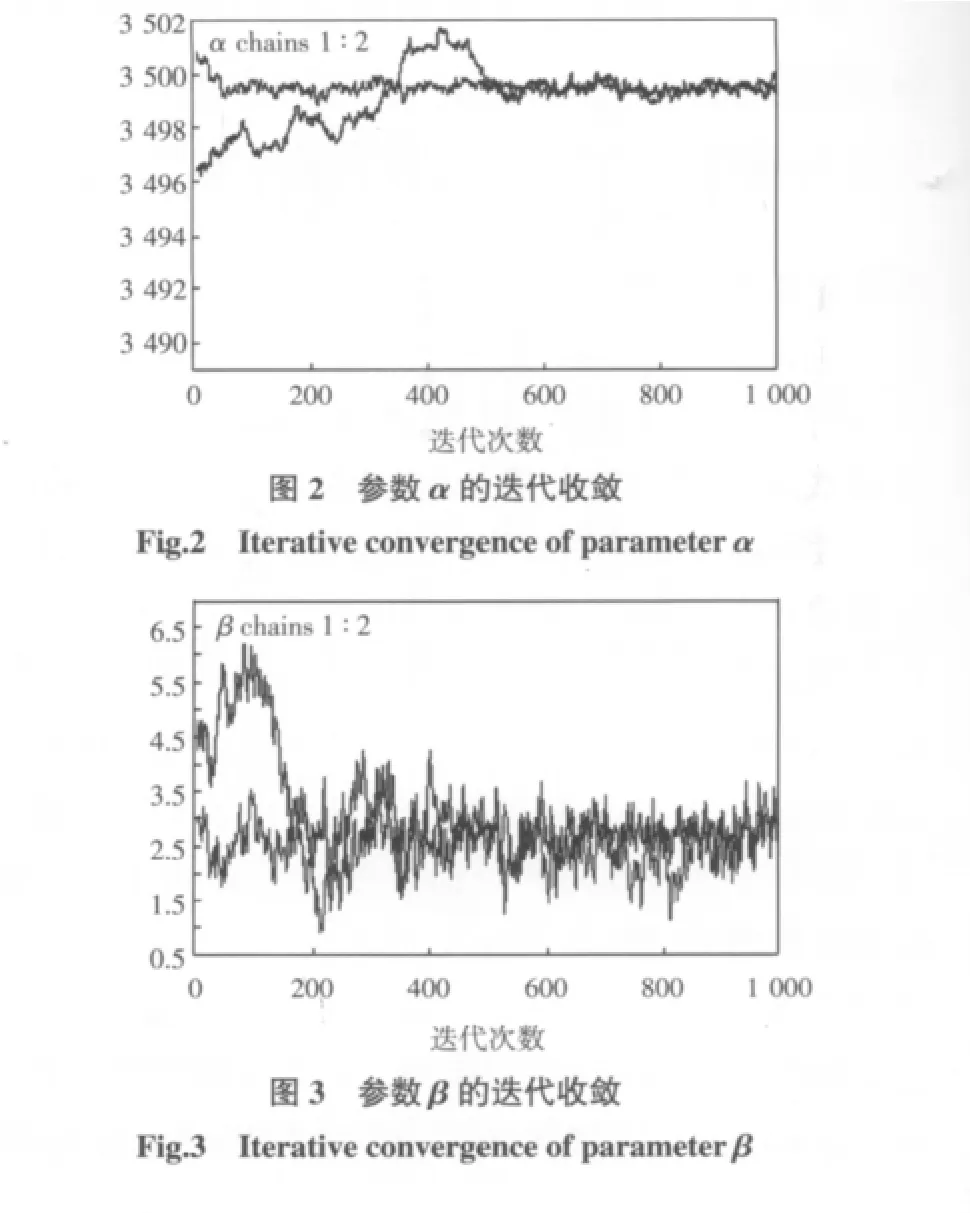
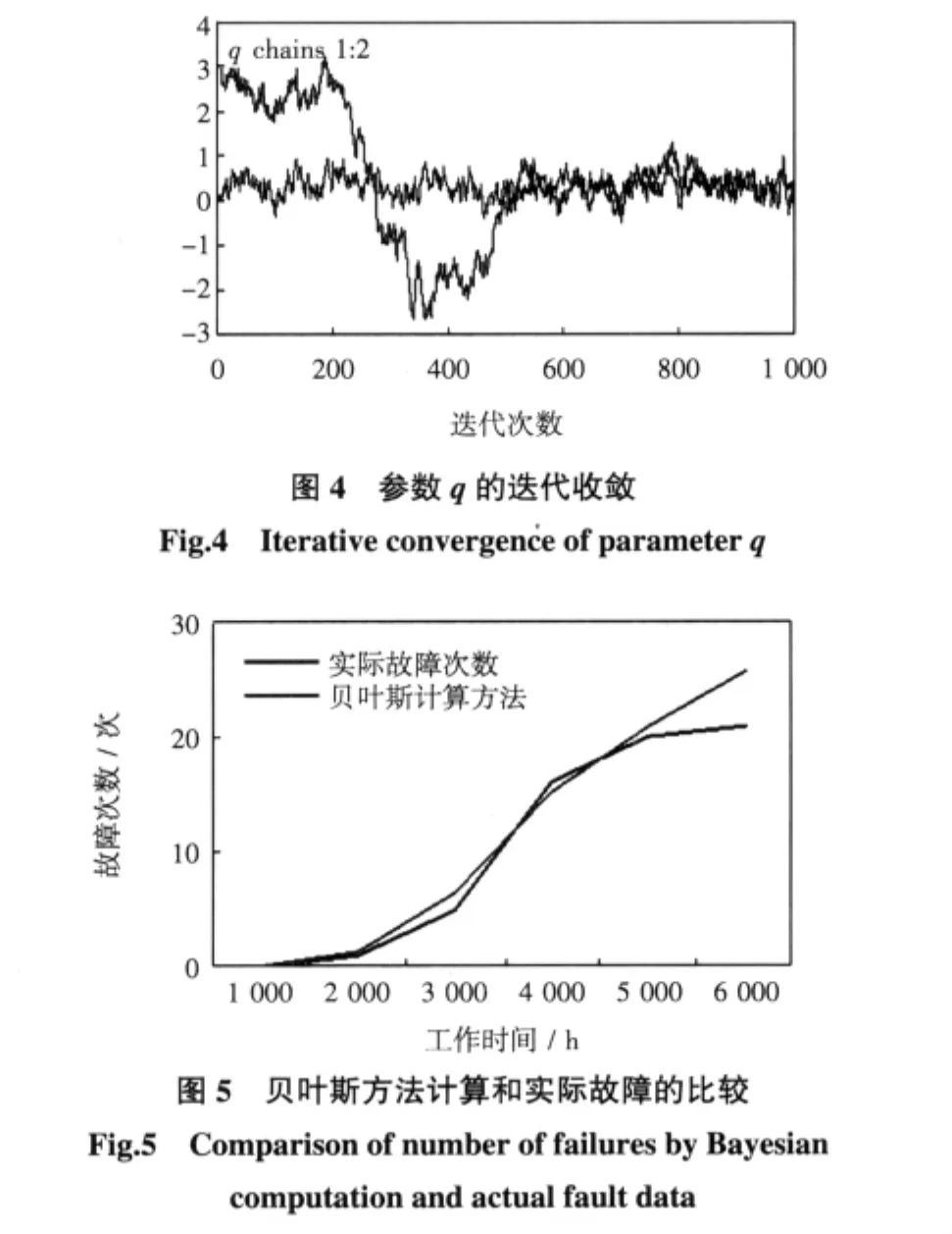
直接计算式(8)比较困难,可以采用切片取样法[8]对其进行求解,切片取样法主要是根据多变量函数的超矩阵进行切片取样,该方法主要根据Markov-Chain Monte-Carlo(MCMC)样本技术,假定从某分布中对变量x取样,在Rn的某个子集中取值,其密度与函数f(x)成比例,在函数f(x)的n+1维区域内进行均匀取样,通过辅助实值变量y,定义在区域U={(x,y):0 其中:x的边际密度函数如式(11)所示 为了对变量x取样,可以在区域(x,y)内进行联合取样,然后忽略变量y。定义一个收敛于Markov-Chain的均匀分布并从U中均匀产生独立点。通过Gibbs样本,从给定x值对y的条件分布进行取样,即让其在区间(0,f(x))内是均匀的;然后从给定y值再对x的条件分布进行取样,也即在区域S={x:y 其中:π(θ,{t1,…,tn})的先验密度函数π0(α,β,q)各个参数相互独立,具体表示如式(13)所示 其中:参数α和q视作均匀分布,故其密度函数为1;参数β服从正态分布,由于0≤β≤10,故可取μβ=0.63和 σβ=0.5。 应用多变量分布使用切片取样法,对于多参变量,定义区间 I=(L,R)通过超矩阵 H={x:Li 1)在(0,f(x0))上均匀取一个实值y,然后定义一个水平切片:S={x:y 2)寻求 x0附近超矩阵,H=(L1,R1)× …×(Ln,Rn),包含全部或部分的切片; 3)在超矩阵从切片中绘制新点x1。 第2步的超区间值,Neal通过4种方法寻找这个区间。对于Weibull分布,考虑所获得先验知识对参数进行限制,分别取 tmin≤α≤tmax、0≤β≤10 以及-2≤q≤5。 由切片取样法产生参数α、β和q后,代入到式(1)和式(2),即建立反映寿命、维修能力的故障寿命分布概率函数,然后再采用文献[4]的计算方法,也即应用式(14)和式(15)计算故障时间,进而求得既定时间内的故障次数[4]。 计算过程如下: 1)如果Σti≥T,则停止产生随机数; 2)如果Σti< T,按照式(14)和式(15)继续产生下一个随机数。 本文取5 000 h内应用在5架飞机上的某个零件故障数据记录,共有25个数据,具体如表1所示,其中失效时间是设备发生故障的时间,这不仅包括首次故障时间,也包括发生故障进行修理后重新使用直至下一次发生故障的时间。另外,表1中的δi数值1表示故障发生没有发生截尾,0表示截尾。对于首先应用数理统计对上述历史故障数据进行分析,由分析知该类航空设备的寿命服从二参数Weibull分布(α,β),然后进一步考察该类设备受到维修能力(即维修度)对产品寿命的影响。 对历史故障取样本容量N=25,在观察周期内记录个体失效的时间,记为t(i),对上述数据进行初步数理统计分析后,初步确立分布参数的范围为:-3≤q≤4,0≤β≤10,min(ti)≤α≤max(ti),应用式(12)先验分布作为三参数模拟的f(x),应用多变量切片取样法,分别对参数α给两个初值3 492和3 501,进行多参数切片样本法模拟参数,模拟过程如图2所示,从图2中可以清楚地看出参数α在迭代次数为540次时,两条链收敛到3 499.27 h左右;类似地,参数β赋予两个初值3和4,其模拟过程如图3所示,在迭代次数为610次时,两条链收敛到2.75左右。维修度q赋予两个初值0.1和3.2,模拟的参数如图4所示,参数q在迭代次数为710次时,两条链收敛到:0.287 1左右。从这3个参数的迭代图中可以清楚地看到每个参数赋予两个初值,经过若干次迭代后具有收敛的特性,故取α为3 499.27,β为2.75,q为0.287 1。然后将这3个参数代入式(1)和式(2),得到了反映故障、维修能力的寿命分布概率密度函数;通过该概率密度函数,应用式(14)和式(15)分别仿真5架飞机的该零件在 1 000、2 000、3 000、4 000、5 000 和 6 000 h 内的故障次数,具体如图5所示,图5中的实际故障次数即表1中的故障,其中贝叶斯计算方法表示用该方法仿真出的数据。 表1 零件故障数据的监控记录Tab.1 Monitoring records of fault data for part 通过图5的比较,二者的数据基本吻合,可以用于小样本故障数据的故障寿命分布概率密度函数建模,同时还能反映维修能力的高低。 针对航空装备历史故障的小样本事件,应用广义更新过程建立反映该设备历史故障以及该设备发生故障后的维修能力的模型,对于分布函数比较复杂的可以通过切片样本法完成,不仅可以处理常用的分布函数,还可处理任意分布函数,另外,本方法最大的特点是建立在已有经验和先验知识的基础上,可以充分反映实际运行情况,在航空装备可靠性建模、故障预测和备件需求量的计算方面使精度得到很大的提高。另外,随着计算机技术的发展,使得应用本方法不仅提高了精度,而且既简单又方便,极大地增加了模型的应用范围。 [1]DINESH KUMAR U,KNEZEVIC J.Availability based spare optimization using renewal process[J].Reliability Engineering and System Safety,1998,59:217-223. [2] 伏宏勇,赵 宇.航空备件计划模型与方法研究[D].北京:北京航空航天大学,2003. [3] BOEING COMPANY.Spares Provisioning ProductsGuide[M].Seattle:Boeing Company,2003. [4] 陈凤腾,左洪福.基于广义更新过程的航空备件需求研究和应用[J].应用科学学报,2007,10:47-49. [5]YANEZ M,JOGLAR F,MODARRES M.Generalized renewal process for analysis of repairable systems with limited failure experience[J].Reliability Engineering and System safety,2002,77:167-180. [6] 邓永录,梁之舜.随机点过程及其应用[M].北京:科学出版社,1992. [7]EDWARD P C KAO.An Introduction to Stochastic Processes[M].Beijing:China Machine Press,2003. [8] ANDREW G J.Generalisation and bayesian solution of the general renewal process for modeling the reliability effects of imperfect inspection and maintenance based on imprecise data[D].USA:University of Maryland,2005. [9]RADFORD M NEAL.Slice Sampling[J].The Annals of Statistics.2003,31(3):705-767. Research and Application of Aero-Spare Based on Bayesian Method CHEN Feng-teng1,ZUO Hong-fu2 There are much more deviations in the calculation of the aero-spares demand by the Poisson formula in recently decades,so we establish the reliability distribution model to reflect the historical failure data and the maintenance capabilities with the application of the generalized renewal process.At the same time for the historical fault data for the current principal is a small sample of events,Bayesian method and slice sampling method were applied to estimate the parameter of the reliability distribution.Finally,with the example analysis, the results show that the number of actual faults and actual failures of the more consistent,increasing the application of this model. Bayesian; aero-spares; failure rate; slice sampling TP3 A 1674-5590(2011)02-0013-05 2010-11-22; 2011-02-27 基金项目:国家自然科学基金项目(60672164);徐州市科技计划项目(XJ09070) 陈凤腾(1971—),男,江苏赣榆人,讲师,博士,研究方向为可靠性、维修性与故障诊断. (责任编辑:杨媛媛)
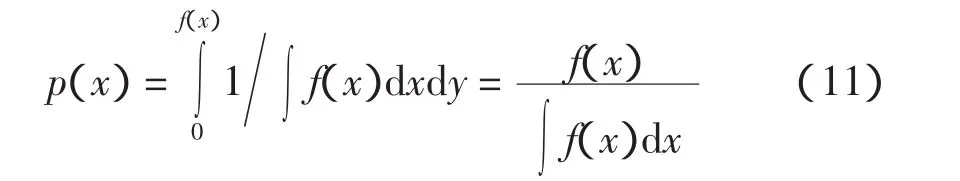
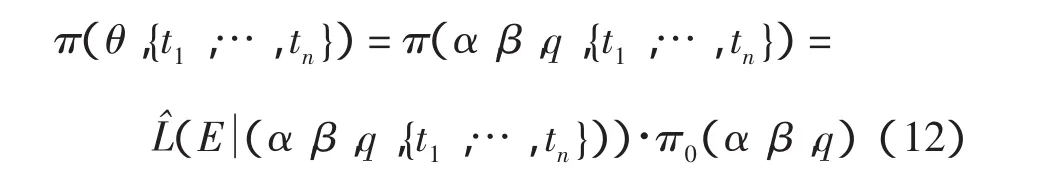
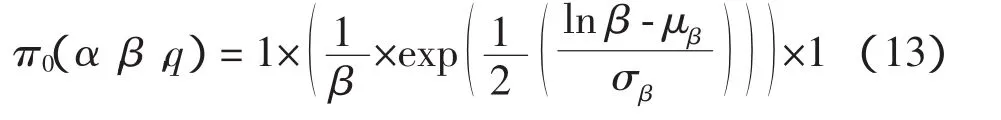
5 故障次数计算
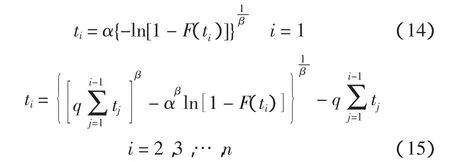
6 实例分析

7 结语
(1.Xuzhou Institute of Technology, Xuzhou 221008,China;2.Civil Aviation College, Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China)
