陶瓷/金属非保守FGM斜板的颤振分析
2011-05-30王忠民
阮 苗 王忠民 王 砚
1.西安理工大学,西安,710048 2.长安大学,西安,710064
0 引言
弹性非保守系统的动力稳定性分析在工程中有着广泛的应用,如梁、板、壳、输液管、桥梁及机翼等,薄板在非保守力作用下的稳定性分析对研究结构系统的颤振现象等问题具有重要的工程意义和理论价值。Leipholz等[1]用拓展的伽辽金法求解出不同边界条件下矩形板在随从力作用下的临界力。王忠民等[2]用Levy法和有限差分法研究了两对边简支且另两对边任意支承的6种矩形薄板在均布切向随从力作用下的动力稳定性问题。文献[3-5]分别对非保守板的颤振和发散失稳问题作了深入的研究。
工程实际中,随着新型复合材料的广泛应用,功能梯度材料板结构的动力分析受到越来越多的关注。Wu等[6]运用移动最小二乘法,分析了功能梯度材料矩形板的动力稳定性。赵凤群等[7]研究了考虑随从力作用的功能梯度材料(FGM)矩形板的动力稳定性。Prakasha等[8]基于一阶剪切变形板理论,运用有限元法研究了简支斜板的热屈曲问题。
本文从薄板理论出发,结合功能梯度材料的特性,通过线性坐标转换关系,建立了斜坐标系下非保守FGM斜板的运动微分方程。运用微分求积法,导出了非保守FGM 斜板的特征值方程,计算了四边固支非保守FGM斜板的固有频率和临界颤振荷载,讨论了斜板夹角、梯度指标和边长比对非保守FGM斜板的临界颤振荷载的影响。
1 FGM斜板的运动微分方程
1.1 材料特性
考虑一受切向均布随从力q0作用的功能梯度斜薄板,如图1所示。板的尺寸为a×b×h,上侧面为陶瓷,下侧面为金属,中间为两种材料构成的梯度层。
设金属、陶瓷的弹性模量分别为E m、E c,质量密度分别为 ρm、ρc,由材料特性的实际情况,可设金属、陶瓷的泊松比相同,则板内任意一点的弹性模量E(z)、质量密度 ρ(z)和泊松比 μ(z)为

图1 受切向均布随从力作用的FGM斜板

式中,k为梯度指标。
1.2 FGM斜板运动微分方程
假设 u0、v0、w0是板中面上沿 x、y、z 方向的位移,则板任一点处的位移为
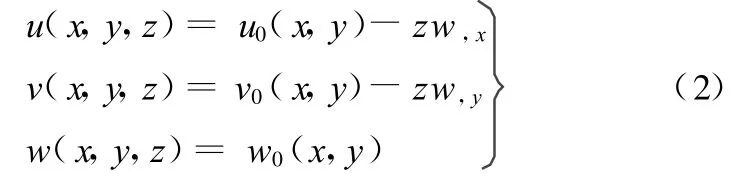
式中,下标“,x” 和“,y”表示分别对 x、y求偏导,下文类似的下标,其含义也类似。
由于三维几何方程中不出现材料常数,因此功能梯度板和匀质板的位移与应变分量几何关系一致。但三维物理方程是变系数的,其中材料常数是厚度z的函数:
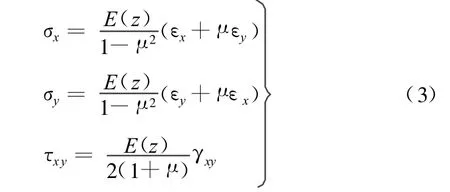
将几何方程、物理方程代入板的薄膜内力和弯曲内力矩公式,可得

根据广义D'Alembert原理,其运动微分方程为

通过坐标变换关系ξ=x-y cotθ,η=y cscθ,得到FGM斜板的运动微分方程:

式中,θ为四边固支斜板夹角。
四边固支斜板的边界条件[9]为
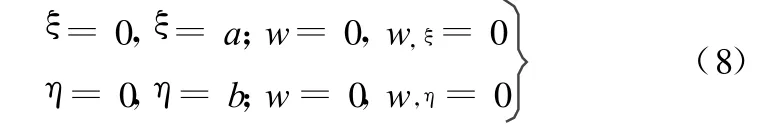
引入量纲一量:

式中,τ为量纲一时间;q为量纲一随从力。
式(7)的量纲一形式如下:
(5)地基处理采用的CFG桩体和土工格栅为线弹性材料,采用摩擦单元模拟桩-土和格栅-土之间的相互作用。

2 数值计算
设式(9)的解为 W(ξ,η,τ)=W (ξ,η)eiωτ,代入式(9)得

对非保守力作用下FGM斜板的量纲一运动微分方程,用微分求积法[10]建立其特征值方程。式程(10)的微分求积形式为

式中,A(1)为第一阶层的加权系数,其他类似;ω为量纲一复频率。
本文在网点布置时,取 N=M,采用δ法[11]处理边界条件。固支边的微分求积形式为
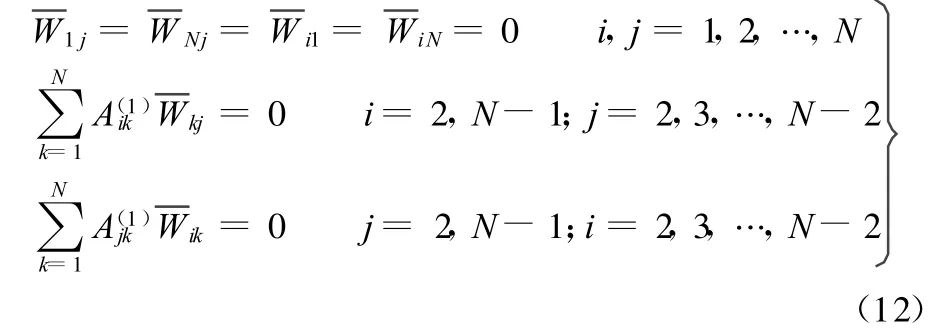
式(11)和式(12)合并成矩阵形式,即

式(13)构成了广义特征值问题。
3 计算结果与比较
数值计算时取陶瓷为ZrO2,金属为Al,材料常数如表1所示。当k=0且θ=π/2时,FGM斜板退化为均质陶瓷矩形板的稳定性问题。取N=11,首先计算四边固支均质陶瓷板的前六阶固有频率,本文结果与文献[11]的比较如表2所示。表3给出了几种不同夹角、不同边长比的四边固支斜板的一阶固有频率与文献[12]的比较情况。表2、表3的比较验证了本文算法的有效性。

表1 材料及材料常数

表2 四边固支斜板的前六阶量纲一固有频率计算结果比较(r=1,k=0,q=0)

表3 四边固支斜板的量纲一固有频率计算结果比较(r=1,k=0,q=0)
图2给出了四边固支斜板夹角θ=75°,边长比r=1,梯度指标k分别为0.5、1.0、1.5时板的前两阶量纲一复频率ω与量纲一随从力q的变化曲线。从图2可以看出,当量纲一随从力q=0时,ω为实数。随着量纲一随从力的增大,板的第一阶和第二阶模态耦合,此时板发生颤振失稳,相应的临界荷载为颤振荷载。当k=0.5时,临界颤振荷载q f=180;当k=1时,临界颤振荷载q f=160;当k=1.5时,临界颤振荷载q f=150。

图2 前两阶量纲一复频率ω与量纲一随从力q的关系曲线(θ=75°,r=1)

图3 前二阶量纲一复频率ω与量纲一随从力q的关系曲线(θ=60°,r=1)
图5 给出了四边固支FGM斜板夹角θ=60°,梯度指标k=1,边长比r分别为0.7、1.0、1.5时板的前两阶模态的量纲一复频率ω与量纲一随从力q的变化曲线。图5表明,边长比的变化使得板的临界颤振荷载值发生变化,失稳形式不变。图6给出了不同夹角板的量纲一随从力(即临界颤振荷载)随梯度指标的变化曲线。图中曲线表明,不同夹角的斜板,随着梯度指标的增大,临界颤振荷载减小,并且当k≤2时变化较大,当k>2时,变化趋于平缓。图7描绘了不同梯度指标板的临界颤振荷载随板夹角的变化曲线。可以看到,不同梯度指标的板,随着夹角的增大,临界颤振荷载减小。图8描绘了不同夹角板临界颤振荷载随边长比的变化曲线。可以看出不同夹角的斜板,随着边长比的增大,临界颤振荷载增大。
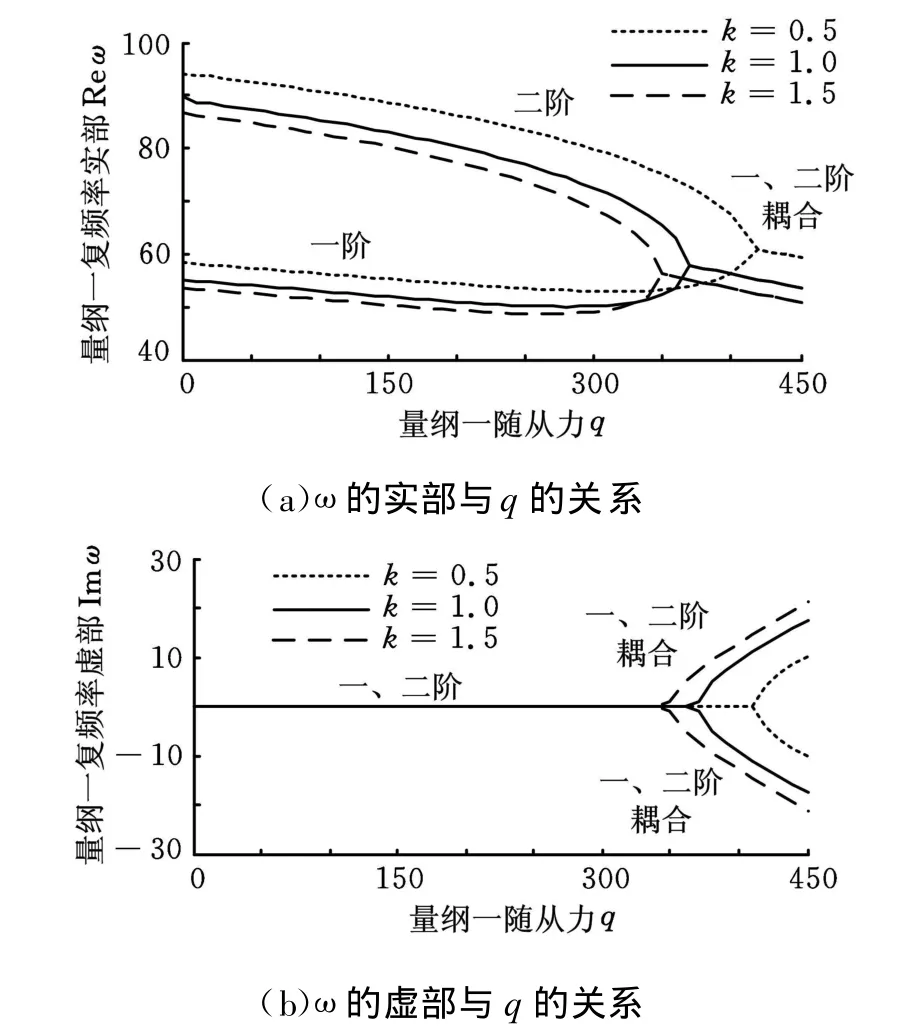
图4 前两阶量纲一复频率ω与量纲一随从力q的关系曲线(θ=45°,r=1)

图5 前两阶量纲一复频率ω与量纲一随从力q的关系曲线(θ=60°,k=1)

6 量纲一随从力q随梯度指标k的变化曲线(r=1)

图7 量纲一随从力q随夹角θ的变化曲线(r=1)
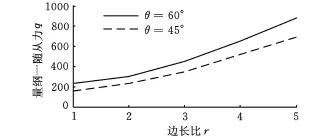
图8 量纲一随从力q随边长比r的变化曲线(k=1)
4 结论
(1)当边长比不变时,对不同夹角的斜板,临界颤振荷载随着梯度指标的增大而减小。
(2)当边长比不变时,对不同梯度指标的板,临界颤振荷载随着斜板夹角的增大而减小。
(3)当梯度指标不变时,对不同夹角的斜板,临界颤振荷载随着边长比的增大而增大。
[1] Leipholz H H,Pfendt F.Application of Extend E-quations of Galerkin to Stability Problems of Rectangular Plates with Free Edges and Subjected to U-niformly Distributed Follower Forces[J].Computer Maths.Appl.Mech.Engry.,1983,37:341-365.
[2] 王忠民,计伊周.矩形薄板在随从力作用下的动力稳定性分析[J].振动工程学报,1992,5(1):78-83.
[3] Zuo Q H,Shreyer H L.Flutter and Divergence Instability of Nonconservative Beams and Plates[J].International Journal of Solids and Structures,1996,33(9):1355-1367.
[4] Kim J H,Kim H S.A Study on the Dynamic Stability of Plate under Follower Force[J].Computers and Structures,2000,74(3):351-363.
[5] Jayaraman G,Struthers A.Divergence and Flutter Instability of Elastic Specially Orthotropic Plates Subject to Follower Forces[J].Journal of Sound and Vibration,2005,281:357-373.
[6] Wu Lanhe,Wang Hongjun,Wang Daobin.Dynamic Stability Analysis of FGM Plates by the Moving Least Squares Differential Quadrature Method[J].Composite Structures,2007,77(3):383-394.
[7] 赵凤群,王忠明,刘宏昭.非保守力作用下FGM矩形板的稳定性分析[J].应用力学学报,2007,24(2):318-322.
[8] Prakasha T,Singhaa M K,Ganapathi M.Thermal Postbuckling Analysis of FGM Skew Plates[J].Engineering Structures,2008,30(1):22-32.
[9] Wang X,Striz A G,Bert C W.Buckling and Vibration Analysis of Skew Plates by the Differential Quadrature Method[J].AIAA J.,1994,32(4):886-889.
[10] 王鑫伟.微分求积法在结构力学中的应用[J].力学进展,1995,25(2):232-240.
[11] 倪振华.振动力学[M].西安:西安交通大学出版社,1990.
[12] Sakata T,Hayashi T.Natural Frequencies of Clamped Orthotropic Skew Plates[J].Journal of Sound and Vibration,1982,81(2):287-298.
