内啮合齿轮泵内齿轮静压支撑研究
2011-05-30张建卓李康康
张建卓 李康康
辽宁工程技术大学,阜新,123000
0 引言
内啮合齿轮泵具有结构紧凑、运转平稳、压力大、噪声低、无困油、自吸性好、转速范围大等突出优点而被广泛应用于各类工程机械中[1]。但由于内啮合齿轮泵中的内齿轮受到油液的液压力和齿轮啮合力的作用,内齿轮外壁对泵体产生较大压力。内齿轮在高转速和高油压条件下运转时,内齿轮外壁对泵体内壁的接触应力和旋转线速度远远超过材料的许用极限值,如润滑不良将产生剧烈摩擦,从而产生黏着磨损,使内齿轮与泵体发生胶合,导致内啮合齿轮泵失效。本课题组研制了一种具有固定间隙的内啮合齿轮泵,其设计最高压力为20MPa,额定压力为16MPa,额定转速为1500r/min,与目前高压内啮合齿轮泵相比,取消了浮动侧板及径向支承块结构,其结构简单,且具有高的机械效率和容积效率。在研制初期的试验过程中,在主轴转速达到1500r/min,输出压力达到14MPa时,内齿轮与泵体由于没有形成全膜润滑而发生胶合失效。为解决这一问题采用了内齿轮静压支撑方法,通过在齿轮泵压油口处与内齿轮外壁接触的泵体内壁上开静压支撑槽并引入高压油,由其产生的液压力与作用于内齿轮的液压力、啮合力产生的合力相平衡,降低了内齿轮与泵体内壁之间的摩擦。同时内齿轮静压支撑为纯液体润滑,内齿轮与泵体内壁之间的润滑油层黏性阻力小,且静压支撑槽内的油液有良好的吸振性能,使内齿轮运转平稳[2],解决了内齿轮的胶合失效问题。本文通过对内齿轮进行受力分析,得到静压支撑槽的开槽位置等参数。
1 内啮合齿轮泵工作原理
如图1所示,一对具有渐开线齿形的外齿轮和内齿轮相互啮合,外齿轮为主动轮,内齿轮为从动轮,之间用月牙块将吸油腔和压油腔隔开,两齿轮转向相同。进入吸油腔的轮齿退出啮合,使吸油腔容积增大,形成真空,液体在大气压力作用下被吸入,两齿轮将吸油腔中的液体带到压油腔。进入压油腔的轮齿进入啮合,压油腔容积减小,液体被压出[3-4]。由于内啮合齿轮泵中的内齿轮受到油液的液压力作用和内齿轮啮合力作用,在高压高速运转时,内齿轮外壁与泵体产生剧烈摩擦,使内啮合齿轮泵发生胶合失效,如图2所示。
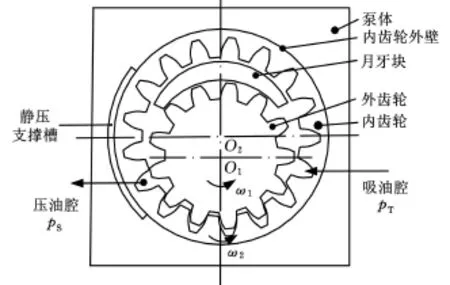
图1 内啮合齿轮泵工作原理

图2 内齿轮胶合图
2 内齿轮圆心角计算
由于在内齿轮受力计算过程中将用到内齿轮的一个齿槽和一个轮齿在齿顶圆上对应的圆心角,故首先计算内齿轮圆心角。
如图3所示,内齿轮的一个齿槽在齿顶圆上对应的圆心角为
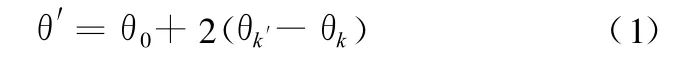

图3 内齿轮尺寸图
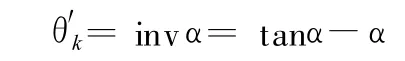
k为渐开线与齿顶圆的交点,θk为渐开线在k点的展角,则 θk=invαk=tanαk-αk。αk为渐开线在k点的压力角

式中,rb为基圆半径;ra为内齿轮齿顶圆半径。
将θ0 、θk′、θk 代入式(1),得到一个内齿轮齿槽在齿顶圆上对应的圆心角为

一个内齿轮轮齿在齿顶圆上对应的圆心角为

其中,α0为一个齿槽和一个轮齿在齿顶圆处对应的圆心角之和
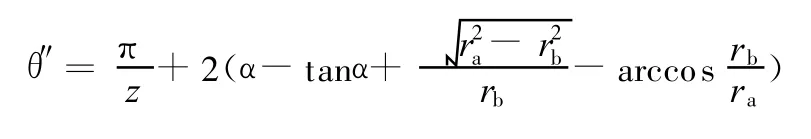
3 内齿轮受力计算
3.1 内齿轮内壁油压力分布规律
如图4所示,内齿轮中心O2与齿顶点A的连线O2 A为吸油腔边界,点O2与齿顶点B的连线O2B为压油腔边界,外齿轮和内齿轮的连心线O1O2为吸油腔与压油腔分界线。O1O2与O2 A之间为吸油腔,其油压 pT=0。O1O2与O2B之间为压油腔,其油压为pS。O2B与O2 A之间为压力过渡区,其压力沿弧线BA方向逐渐由压油腔压力pS衰减到吸油腔压力零。内齿轮内壁在起始位置的油压分布如图4所示。
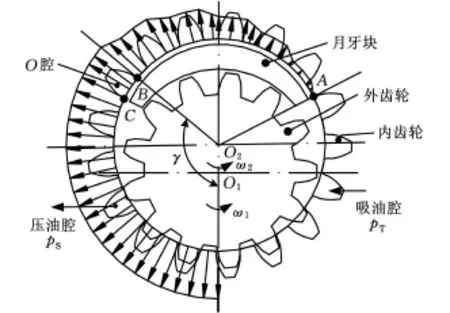
图4 内齿轮在起始位置的油压分布图
压力过渡区中月牙块与内齿轮轮齿齿顶之间的区域为齿顶缝隙区,实际上齿顶缝隙区很小,为表达清楚,将其放大。当油液流过该缝隙区时,其压力呈线性衰减状态[6],则各个齿顶缝隙区任一位置的压力为

式中,Δθ′为该位置与吸油腔边界O2A之间只计算齿顶缝隙区的圆心角之和;θf为过渡区中所有齿顶缝隙区的圆心角之和。
压力过渡区中月牙块与内齿轮齿槽之间的区域为齿槽区。由于其内部空间远大于齿顶缝隙区形成的空间,故齿槽区产生的压力损失可忽略,则各个内齿轮齿槽区等压。各个齿槽区的压力为

式中,Δθ为该齿槽区与吸油腔边界O2A之间所有齿顶缝隙区的圆心角之和。
压力过渡区中的齿顶缝隙区和齿槽区从吸油腔边界O2 A到压油腔边界O2B依次交替排列。在内齿轮转动过程中,O2 A、O2B之间的夹角也随之发生变化,导致内齿轮内壁所受油液压力的合力随压油腔、过渡区所对应的圆心角的变化而变化,且以内齿轮转过一个齿槽和一个轮齿为一个周期。下面以压油腔处的月牙块端面与内齿轮轮齿正好脱离为起始位置,以转过一个齿槽和一个轮齿两种情况进行受力分析。两种情况下内齿轮所受液压力分为压油腔液压力对内齿轮的作用力和过渡区液压力对内齿轮的作用力两部分。
3.2 内齿轮转过一个齿槽的过程中的受力分析
首先分析压油腔液压力对内齿轮的作用力。由于压油腔液体压力恒定,因此只要确定压油腔区间角即可确定其受力。如图4所示,以内齿轮轮齿齿顶C点刚好转过压油腔处的月牙块端面为起始位置,此时图中O腔正好与压油腔沟通,则O腔油压为pS。O1O2与O2B之间的压油腔区间角γ达到最大。
如图5所示,随着内齿轮转动,O2B沿逆时针方向转动,则压油腔区间角γ逐渐减小,当转过一个内齿轮齿槽角θ′后,B点刚好转到压油腔处的月牙块端面的延长线上,压油腔区间角 γ达到最小。当内齿轮转过的角度θ小于一个齿槽在齿顶圆上对应的圆心角θ′即0<θ<θ′时,压油腔液压力作用于内齿轮上的 x、y方向分力大小分别为

式中,φ0为吸油腔处的月牙块端面与 x轴的夹角;φ1为月牙块圆心角;β为所求区域中任一点与O2点的连线和x轴之间的夹角;b为内齿轮的宽度。
下面分析过渡区液压力对内齿轮的作用力。由齿轮泵结构知,月牙块圆心角为一个齿槽和一个轮齿在齿顶圆上对应的圆心角的整数倍,则在内齿轮转过一个齿槽的过程中,过渡区中包含的齿顶缝隙区数过渡区中包含的齿槽区数n′=n-1;过渡区中所有齿顶缝隙区的圆心角之和 θf=nθ″。
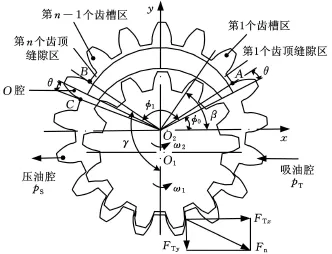
图5 内齿轮在转过一个齿槽过程中的示意图
由式(3)得过渡区中第i(i=1,2,…,n-1)个齿槽区的压力为
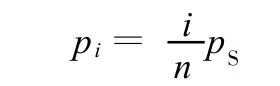
则齿槽区液压力作用于内齿轮x、y方向的分力分别为
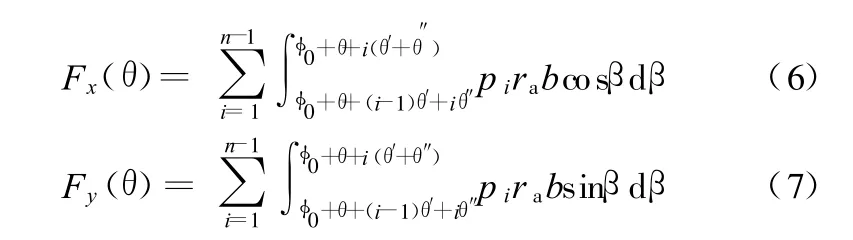
由式(2)得过渡区中的第i(i=1,2,…,n)个齿顶缝隙区的压力分布为
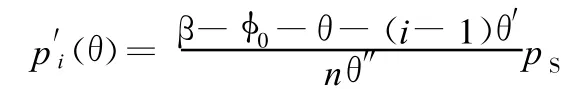
齿顶缝隙区压力作用于内齿轮上的x、y方向分力分别为

3.3 内齿轮转过一个轮齿的过程中的受力分析
首先分析压油腔液压力对内齿轮的作用力。如图6所示,内齿轮从起始位置转过一个齿槽后,齿顶D点正好在压油腔处月牙块端面的延长线上,此时压油腔区间角最小。
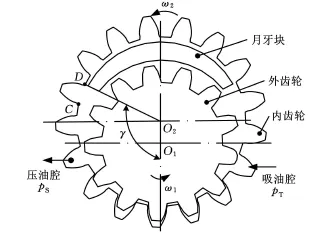
图6 内齿轮转过一个齿槽后的位置
如图7所示,在内齿轮从图6位置转过一个轮齿的过程中,压油腔区间角γ范围始终不变。则当内齿轮从起始位置转过的角度大于一个齿槽在齿顶圆上对应的圆心角,且小于一个齿槽和轮齿在齿顶圆上对应的圆心角时,即 θ′<θ<θ′+θ″时,压油腔液压力作用于内齿轮的 x、y方向分力分别为

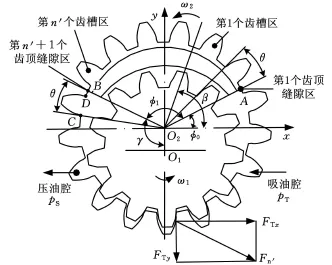
图7 内齿轮转过一个轮齿的过程
下面分析过渡区液压力对内齿轮的作用力。在内齿轮转过一个轮齿的过程中,过渡区中包含的齿槽区数过渡区中包含的齿顶缝隙区数n′=n′+1,过渡区中所有齿顶缝隙区的圆心角之和 θf=n′θ″。
由式(3)得过渡区中第 i(i=1,2,…,n′)个齿槽区压力为

齿槽区液压力作用于内齿轮的分力为

由式(2)得过渡区中第一个齿顶缝隙区的压力分布为

过渡区中第i(i=2,3,…,n′)个齿顶缝隙区的压力分布为

在第n′+1个轮齿齿顶缝隙区的压力分布为
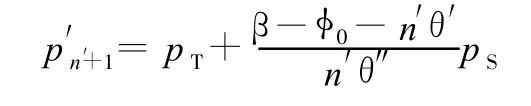
齿顶缝隙区液压力作用于内齿轮上的x方向分力为

式中,Fx1(θ)为过渡区中第1个齿顶缝隙区液压力作用于内齿轮的x方向分力;Fxi(θ)为过渡区中第2个齿顶缝隙区到第n′个齿顶缝隙区液压力作用于内齿轮的x方向分力;Fxn′+1(θ)为过渡区中第n′+1个齿顶缝隙区液压力作用于内齿轮的x方向分力。
齿顶缝隙区液压力作用于内齿轮的y方向分力为
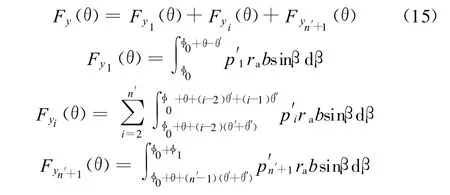
式中,Fy1(θ)为过渡区中第1个齿顶缝隙区液压力作用于内齿轮的y方向分力;Fyi(θ)为过渡区中第2个齿顶缝隙区到第n′个齿顶缝隙区液压力作用于内齿轮上的y方向分力;Fyn′+1(θ)为过渡区中第n′+1个齿顶缝隙区液压力作用于内齿轮的y方向分力。
3.4 齿轮啮合力作用于内齿轮的x、y方向分力
内齿轮在工作过程中不但受到油压作用,而且与外齿轮啮合,因此还受到啮合作用力。齿轮啮合力作用于内齿轮的 x、y方向分力分别为[7]
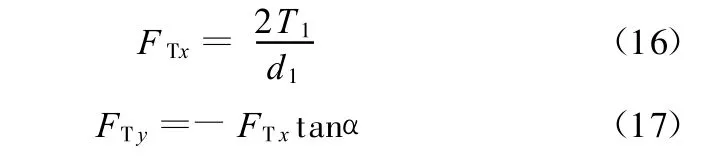
式中,d1为外齿轮分度圆直径,mm;T1为外齿轮所受转矩,为外齿轮转速(主轴转速),r/min;P1为输入功率,为齿轮泵输出压力,p=pS(MPa);Q为齿轮泵流量,L/s;η为齿轮泵机械效率;α为内齿轮压力角。
3.5 作用于内齿轮的x、y方向总分力
内齿轮在转过一个齿槽的过程中,受到x方向上的总分力F x为式(4)、式(6)、式(8)、式(16)之和。内齿轮受到y方向上的总分力Fy为式(5)、式(7)、式(9)、式(17)之和。
内齿轮在转过一个轮齿的过程中,受到x方向上的总分力Fx为式(10)、式(12)、式(14)、式(16)式之和,内齿轮受到y方向上的总分力F y为式(11)、式(13)、式(15)、式(17)之和 。
3.6 静压支撑槽角度计算
为防止内齿轮在高速运转过程中由于摩擦而发生胶合,可在压油腔与内齿轮外壁接触的泵体内壁上开设静压支撑槽,将高压油引入该静压支撑槽中,使支撑槽内的高压油液对内齿轮外壁产生的液压力F J与内齿轮内壁所受的液压力及啮合力所产生的合力F相平衡,以达到对内齿轮静压支撑的目的,由于F大小和方向随内齿轮转动而变化,并且在某角度内变化,如图8所示,与之相平衡的静压支撑力FJ的方向与合力F的摆动中心线重合,大小与F的平均合力相等。则静压支撑力F J为
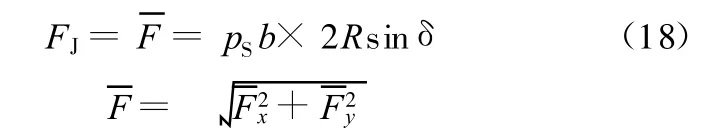

图8 静压支撑槽角度
故静压支撑槽角度大小为2δ,且以合力F的摆动中心线为开槽角度的中心线。
4 试验研究
本课题组研制的内啮合齿轮泵的参数如下:内齿轮压力角为α=20°,模数m=5mm,外齿轮齿数为13,内齿轮齿数为17。内齿轮齿顶圆半径r a=40mm,内齿轮的外壁圆半径R=55mm,压油腔额定压力pS=16MPa,齿轮宽度b=30mm,φ0=26.47°,φ1=127.06°,外齿轮转速 n1=1500r/min,取齿轮泵机械效率η=0.95。齿轮泵流量Q=1.3L/s。
根据上述分析结果,通过MATLAB编程计算得到内齿轮在转过一个齿槽和一个轮齿过程中x、y方向上所受的平均作用力合力F的摆动中心线与x轴夹角为 δ0=186°。
由式(18)得泵体内壁上所开静压支撑槽角度的一半δ=38.8122°,所以得到使内齿轮完全处于平衡状态时,静压支撑槽角度在147.1878°~224.8122°之间。上面的计算值未考虑高压油液由静压支撑槽向低压区过渡时对内齿轮所产生的附加压力,同时为防止在高压区内齿轮外壁与泵体内壁之间产生间隙泄漏降低齿轮泵的容积效率,应使高压油作用于内齿轮内壁的液压力及其所受啮合力所产生的合力稍大于静压支撑力,实际使用时应将理论计算得到的静压支撑槽夹角适当缩小。经过多次试验,实际所开静压支撑槽角度调整为156°~216°之间较为合适,如图9所示。另外,为使静压支撑槽和内齿轮外壁形成全膜润滑,静压支撑槽厚度为0.2mm。试验结果表明,此值既保证了内啮合齿轮泵高的机械效率又保证了高的容积效率。在内啮合齿轮泵输出压力为20MPa、转速为1500r/min时,齿轮与泵体长时间运行未发生胶合失效情况,且泵体外壁温升低于55℃。实测齿轮泵在额定压力16MPa下长时间运转时的容积效率为0.95,总效率达0.92。

图9 静压支撑槽
5 结束语
本文分析了内啮合齿轮泵内齿轮与泵体发生胶合失效的原因。针对内齿轮内壁实际受力情况,压力过渡区中的齿顶缝隙区的压力按线性变化、齿槽区压力为等压,对内齿轮受力随转动角度变化情况作了动态分析。利用MATLAB软件计算得到内齿轮内壁所受合力大小方向在一个周期内的变化情况,并得到其在 x、y方向上的平均分力和合力F摆动中心线角度。设计了静压支撑槽的开槽角度及位置。试验研究表明,该齿轮泵在输出压力20MPa、转速1500r/min时运行正常,无失效发生。
[1] 罗骥,袁子荣,吴盛林.水液压内啮合齿轮泵的设计与研究[J].中国机械工程,2003,14(11):912-914.
[2] 钟洪,张冠坤.液体静压动静压轴承设计使用手册[M].北京:电子工业出版社,2007.
[3] 许贤良,赵连春,王传礼.复合齿轮泵[M].北京:机械工业出版社,2008.
[4] 李庆,李宏伟,翁振涛.内啮合齿轮泵:中国,02137342.6[P].2003-04-23
[5] 孙恒,陈作模,葛文杰.机械原理[M].北京:高等教育出版社,2007.
[6] 张克危.流体机械原理(下)[M].北京:机械工业出版社,2001.
[7] 濮良贵,纪名刚.机械设计[M].北京:高等教育出版社,2007.
