基于应变梯度塑性理论的微切削第一变形区应变分布研究

吴继华 王文奎 刘战强

1．绍兴文理学院，绍兴，312000 2．山东大学，济南，250061

0 引言

切削过程不仅是材料的去除过程还是材料的变形过程，工件材料在刀具作用下发生剧烈变形，出现应变大、应变率高及温度改变等现象。切削过程中的变形程度是合理选择切削输入参数、控制切削加工质量的重要依据，揭示微切削变形规律有利于合理选择切削输入参数，准确预测微切削性能参数。

微切削不仅具有宏观切削加工的一般特点，如大应变、高应变率以及温度变化显著等，还具有微观加工特征，如尺度效应、犁切效应、最小切削厚度效应等。因此微切削变形机理与宏观切削变形显著不同，不能照搬宏观切削机理［1］。

宏观切削实验研究表明，切削过程中第一变形区变形剧烈，受测量仪器和测量方法的限制，要实时准确地测出切削过程中高温度、大应变、高应变率等极端条件下的变形情况相当困难。Piispanen等认为切削中的变形发生在理想的剪切平面上，而Lee等假定宏观切削过程中工件材料产生的变形均匀，着重研究切削速度、进给量、机床性能、温度等切削过程参数对加工结果的影响［2］。随着科技的发展，先进的实验测试手段不断应用于切削过程变形的测量，很多学者得出了宏观切削过程中第一变形区的变形分布不均匀的结论。文献［3］用快速落刀法获得宏观切削过程中的切屑根部试样，研究切屑根部流线图，用数学方法确定流线图不同位置的剪切角，并由此计算剪应变，得出第一变形区剪应变的不均匀分布。微切削领域中对第一变形区变形分布规律的研究很少，且由于微切削较宏观切削加工尺度微小，受限于测量技术的发展，宏观切削过程中切削变形的常规测试方法难以适用于微切削过程变形的测量，需要寻找更合理的方法来研究微切削过程中的切削变形分布规律。

本研究用有限元仿真方法研究了微切削45钢时第一变形区的有效流动应力、有效应变分布及其变化规律，分析了切削厚度与切削刃口圆弧半径比对有效流动应力、应变分布的影响。

1 正交微切削过程仿真

为了建立正交微切削有限元分析模型，假设微切削过程具备如下的条件:①切削过程形成连续的切屑，无积屑瘤存在;②切削温度不足以导致工件材料发生金相组织变化、退火软化和其他一些化学变化;③为了加快计算速度和保证计算的收敛，视刀具为刚体。

应用ABAQUS/Explicit有限元软件对正交微切削过程进行仿真。刀具采用无涂层硬质合金刀具，工件材料选用45钢，材料特性参数如表1所示［4］。

表1 刀具、工件材料特性参数

为了表示应变梯度对微观尺度材料变形特性的影响，应用应变梯度塑性理论建立工件材料本构模型。应变梯度塑性理论自提出以来成功解释了金属材料微观尺度的尺度效应，即材料强度随尺寸的减小而增大的现象。微切削中工件切除的特征长度在微米级，许多研究者已用实验证明:当切除尺寸减小到一定值时发生显著尺度效应。应变梯度塑性理论将材料剪切流动应力表达为位错密度的函数，认为材料的塑性硬化来源于统计存储位错与几何必需位错，前者与塑性应变有关，后者与塑性应变梯度有关［5］。应用应变梯度塑性理论可以成功预测微切削中的尺度效应。包含应变梯度的材料流动应力计算表示为［6］

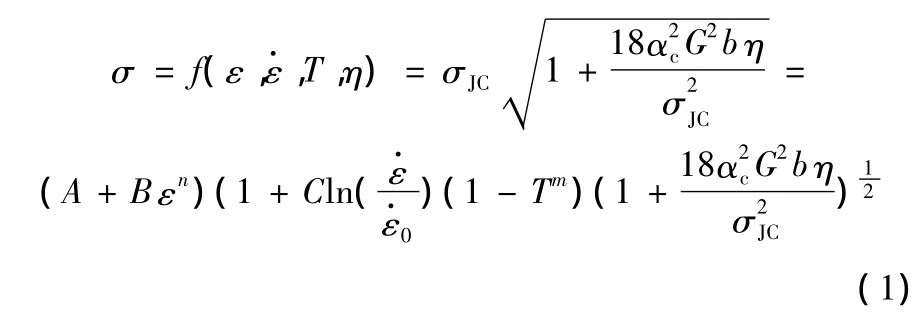
式中，A、B、C、m、n、αc为材料系数;G为剪切模量;b为伯格斯常量;ε、ε·分别为有效应变和应变率;η为有效应变梯度;σJC为用宏观Johnson－Cook模型计算的有效流动应力;T为量纲一温度项。

通过正交窄槽微铣削实验测得微切削力及切屑厚度，并应用模型逆辨识技术计算得到正交微切削本构方程中的材料系数。采用ABAQUS提供的用户材料子程序VUMAT对所建立的基于应变梯度塑性理论的材料本构模型进行二次开发，编写微观尺度材料本构关系程序，通过内部变量控制单元的失效状态，程序流程如图1所示。

图1 用户子程序流程图

微切削摩擦模型采用黏着－滑移模型，为了符合实际微切削摩擦情况，获得更高的仿真精度，摩擦因数μ由微切削实验测得的切削力求出，本研究取实验摩擦因数的平均值0.3。切屑分离标准采用物理分离准则。

2 仿真结果与分析

2．1 微切削第一变形区的有效应力分布

根据微切削过程中切削厚度与切削刃口圆弧半径比(t/re)，分以下三种情况研究微切削第一变形区的有效应力分布。

(1)t/re＞ 1。图2为切削厚度t=20μm，切削刃口圆弧半径re=2μm时的正交微切削有效流动应力仿真结果。当切削厚度大于切削刃口圆弧半径时，最大有效流动应力发生在切削刃口前方圆弧形区和平行区域。有效流动应力沿垂直于平行区方向呈梯度减小趋势。离此平行区域中心线距离越远，有效流动应力越小。有效流动应力与距平行剪切区中心线上一点O的距离l的关系如图3所示。

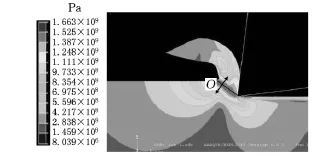
图2 t=20μm、r e=2μm时的有效流动应力分布

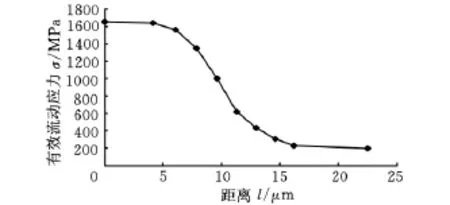
图3 t=20μm、r e=2μm时有效流动应力与距离l的关系

(2)t/re=1。图4为切削厚度为10μm，切削刃口圆弧半径为10μm，即切削厚度等于切削刃口圆弧半径情况下的正交切削有效流动应力仿真结果。由图4可见，在切削刃前方出现的应力突然变小点A把平行区域分开。最大有效流动应力区域开始转变到切削刃口圆弧的前方，成为圆弧形状。

图4 t=10μm、r e=10μm时的有效流动应力分布

(3)t/re＜1。由图5可见，当切削厚度小于切削刃口圆弧半径时，最大有效流动应力区发生在切削刃口圆弧半径前方，呈圆弧状。有效流动应力沿圆弧周向均匀分布，沿径向则存在较大的应力梯度。第一变形区模型可以简化为以刀具与工件接触面的中心为圆心、以接触长度的一半为半径(ra)的圆弧区域。

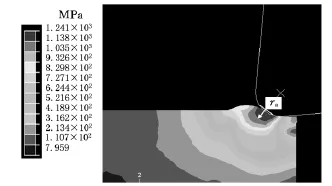
图5 t=6μm、r e=16μm时的有效流动应力分布

沿圆弧变形区径向的有效流动应力与距切削刃口圆弧距离的关系如图6所示。可以看出随着与切削刃口圆弧的距离的增大，有效流动应力逐渐减小。

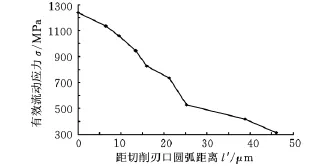
图6 t=6μm、r e=16μm时的有效流动应力与距离l'的关系

2．2 微切削第一变形区的有效应变分布

(1)t/re＞1。由图7可以看出，在切削厚度与切削刃口圆弧半径比大于1时，最大有效应变发生在前刀面上，切削刃口前方的材料应变不大。

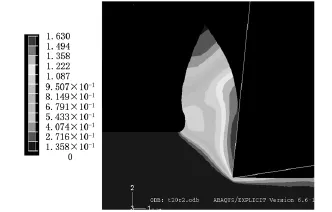
图7 t=20μm、r e=2μm时的有效应变分布

(2)t/re=1。由图8可得，当切削厚度与切削刃口圆弧半径比等于1时，最大有效应变不发生在刀具前刀面上，而发生在切削刃口前方。沿AB方向上的应变变化与距切削刃口圆弧半径距离的关系如图9所示。

由图9可以看出，工件材料的有效应变在距离切削刃口圆弧最近处得到最大值，离切削刃口圆弧距离越大变得越小。

(3)t/re＜1。当切削厚度与切削刃口圆弧半径比小于1时，有效应变场分布如图10所示，可见最大有效应变发生在切削刃口圆弧半径前方，为以刀具和工件的接触面的中心为圆心，按与切削刃口圆弧的距离从小到大而依次减小。在一系列同心圆弧周向上的有效应变变化不大，可见切削刃口圆弧的存在使应变在圆弧周向分布更加均匀。

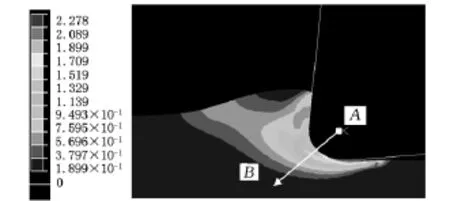
图8 t=10μm、r e=10μm时的有效应变分布

图9 t=10μm、r e=10μm时有效应变与距切削刃口圆弧半径距离的关系

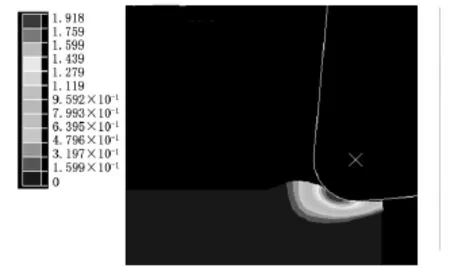
图10 t=6μm、r e=16μm时的有效应变分布

沿刃口圆弧直径方向上的应变变化与距切削刃口圆弧的距离的关系如图11所示。比较图9和图11可以得出:当切削厚度与切削刃口圆弧半径比减小时，最大有效应变变化不大，然而变形区厚度减小，应变梯度增大。

3 微切削根部实验

为了验证基于应变梯度塑性理论的正交微铣削仿真结果，我们进行了正交微铣削实验，获得切屑根部。微切削机床采用KERN公司生产的微细加工中心，刀具采用肯纳公司生产的整体硬质合金刀具，型号为F2AT0300AWL00R005，铣刀刀杆直径为3mm，齿数为2。刀具样本未提供切削刃口圆弧半径参数，实验前需解决切削刃口圆弧半径的测量问题。首先把刀具沿垂直于切削刃长度方向刃磨成一平面，在显微镜下采集切削刃图像，用MATLAB图像处理程序测量切削刃口圆弧段的半径，如图12所示，测得实验所用的整体硬质合金刀具切削刃口圆弧半径为7μm。

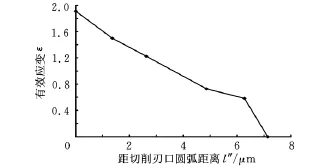
图11 t=6μm、r e=16μm时有效应变与距切削刃口圆弧的距离的关系

图12 切削刃口圆弧半径的测量

工件材料选用正火态45钢。使切削刃垂直于切削方向整条切入切出，构造正交切削条件，正交铣削方案见图13a。通常应用快速落刀法获得切屑根部，即利用“快速落刀”装置的特殊刀架，在切削过程中某一瞬间使刀具以极快的速度突然脱离工件，把某一切削条件下切削层的变形情况“冻结”下来。快速落刀装置落刀速度的快慢对切屑根部变形有较大影响，故提出利用工件特殊形状，使工件产生突然断裂方法获得切屑根部，此方法可以消除落刀装置速度快慢对切屑根部变形的影响(专利号ZL200710017149.0)。首先把工件加工成带圆孔的特定形状，刀具沿圆孔的中心线方向运动，当刀具切削到圆孔最大直径处时，发生突然断裂，使切屑根部从工件上分离，见图13b。

所得的试样较微小，为便于下一步的打磨、显微硬度测试等工作，将得到的切屑根部试样在XQ－2B型半自动金相镶嵌机上进行镶嵌处理。在显微镜下确定距离切屑断裂处最近的圆弧状区域为微切削第一变形区。利用MH－6型显微维氏硬度计来测量切屑根部试样的圆弧变形区，获得各选定点的显微维氏硬度值。所加载的质量设为10g，压入时间 5s。

图13 刀具与工件安装相对位置

Tabor提出，理想弹塑性材料的有效流动应力σ和硬度H间存在线性关系，材料系数取3［7］，则有

微切削过程中的有效流动应力、应变关系为

式中，σref为材料参考流动应力。

当有效流动应力变化时，有效应变也随之变化。微切削切屑根部显微硬度测试结果见图14，有效流动应力分布见图15。

图14 微切削切屑根部显微硬度测试(v c=188．4m/min，f z=2μm)

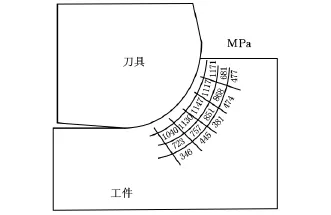
图15 微切削第一变形区有效流动应力分布(v c=188．4m/min，f z=2μm)

通过测试微切削实验切削参数下的切屑根部圆弧变形区的显微硬度，计算有效流动应力，可得出以下两个结论:

(1)沿切削刃口圆弧周向的有效流动应力变动范围不大，说明切削刃口圆弧半径的存在使有效流动应力分布更加均匀。

(2)沿切削刃口圆弧径向的有效流动应力变化显著，存在应变梯度。有效流动应力最大值产生在离切削刃口圆弧最近处。

正交微铣削实验结果验证了应变梯度的存在，证明了应变梯度塑性理论表示微切削过程中材料在微观尺度的变形特性的有效性。

4 结束语

建立了基于应变梯度塑性理论的材料本构模型，用该模型表征了工件材料的微观尺度特性，进行了正火态45钢的微切削过程仿真，研究了第一变形区的有效流动应力、有效应变分布及其变化规律;分析了切削厚度与切削刃口圆弧半径比对流动应力、应变分布的影响。

［1］ 吴继华，刘战强．基于应变梯度塑性理论的正交微切削中最小切削厚度预测［J］．中国机械工程，2009，20(18):2227-2230．

［2］ Childs T，Maekawa K，Obikawa T，et al．Metal Machining:Theory and Applications［M］．Arnold:Butterworth－Heinemann，2000．

［3］ Elmadagli M，Alpas A T．Metallographic Analysis of the Deformation Microstructure of Copper Subjected to Orthogonal Cutting［J］．Materials Science and Engineering，2003，355:249-259．

［4］ Woon K S，Rahman M，Fang F Z，et al．Investigations of Tool Edge Radius Effect in Micromachining:a FEM Simulation Approach［J］．Journal of Materials Processing Technology，2008，195(1/3):204-211．

［5］ Taylor G I．The Mechanism of Plastic Deformation of Crystals．Part I．Theoretical［J］．Proceedings of the Royal Society of London，Series A，1934，145，362-387．

［6］ Liu K．Processes Modeling of Micro－cutting Including Strain Gradient Effects［D］．Georgia:Georgia Institute of Technology，2005．

［7］ Tabor D．The Hardness of Metals［M］．Oxford:Oxford University Press，2000．