多工况下变速箱箱体结构的拓扑优化设计

张喜清 项昌乐 刘 辉

1．太原科技大学，太原，030024 2．北京理工大学车辆传动国家重点实验室，北京，100081

0 引言

变速箱系统是履带车辆整个传动系统的重要组成部分，其箱体结构在保障变速箱系统稳定高效的工作中起着重要作用。箱体结构既是整个变速箱的外壳，又是齿轮、传动轴等内部齿轮传动系统的承载体。箱体在车辆行驶过程中承受各种动载荷作用，这必将影响系统运行的稳定性和安全性。在实际工程设计中，箱体结构的设计往往比较保守，造成了材料的浪费及结构增重，因此在考虑箱体结构多工况载荷特性的基础上对其进行拓扑优化设计具有很重要的工程意义。

结构拓扑优化是一种根据约束、载荷及优化目标寻求结构材料最佳分配的优化方法，一般应用在产品结构设计的初始阶段，处于概念设计阶段，目前这方面已有了很多研究成果［1-4］。而对现有产品结构进行拓扑优化设计的研究相对较少［5-6］，能实现结构多载荷工况下的优化设计的研究更少［7］。本文建立了变速箱箱体初始结构的有限元模型，选择结构各工况动态仿真的最大载荷作为载荷边界条件，对其进行了静力分析和模态分析，并基于optistruct平台对箱体进行多载荷工况拓扑优化设计。

1 箱体有限元模型建立

1． 1 网格划分

本文所研究的变速箱箱体由上箱体、下箱体、左端盖、右端盖、前盖五部分组装而成，几何结构比较复杂，需要进行必要的简化操作。本文采用的简化措施是去除结构中螺栓孔、内置油路、倒角等特征，然后用Hypermesh进行网格划分。采用六面体单元进行网格划分是最理想的方式，它可以用较少的单元获得较高的计算精度。最终该有限元模型共有111 916个实体单元，其中六面体实体单元占93%，五面体单元(楔形体)占7%，箱体有限元模型如图1所示。箱体的材料为铸铝，材料密度ρ=2.7×103kg/m3，弹性模量 E=70GPa，泊松比μ =0.3。

为了方便在轴承座上施加约束和边界载荷，模型中添加刚性单元rbe2来定义位移约束位置，添加刚性单元rbe3来定义载荷作用位置。rbe2和rbe3单元都属于多点约束(multi－point constraint，MPC)的形式，通过蜘蛛网状的连接中心的主节点来控制所有从节点。rbe2单元中主从节点的位移始终保持一致，rbe3单元中主节点的位移是从节点位移的线性组合。该箱体模型共添加3个用于固定约束的rbe2单元，分别在左右端盖和前盖处;添加19个用于载荷施加的rbe3单元，分别位于箱体的各轴承座孔处。

图1 箱体有限元模型

1． 2 载荷边界条件

对箱体结构进行静力学分析时，结构载荷边界条件的确定尤为重要，本文通过对变速箱内齿轮传动系统进行刚柔耦合多体动力学仿真来获得箱体各轴承座处的时域载荷数据。由于该变速箱体有7个挡位工况，其中液力工况为倒挡、1挡、2挡、3挡，机械工况为4挡、5挡、6挡，每种挡位工况有着不同的动力传递路线，且传递着不同的载荷，故箱体各工况所受载状况也不同，从而影响箱体结构响应结果。

对箱体进行静力学分析时，静态载荷选择各轴承座动力学仿真分析所得时域动态力的最大值，在倒挡、发动机转速2000r/min的工况下，箱体19处轴承座处各方向的静态载荷分布如图2所示。

图2 倒挡工况下各轴承座处静态载荷

图2 中1～11为后传动变速部分的各轴承座位置，12～19为前传动部分的各轴承座位置。静力最大值发生于X方向，幅值达98 463N，位于后传动变速部分Ⅰ轴中间轴承座处。同理可获得其他6个挡位工况下各轴承座处的静力最大值。

2 箱体模态与静力分析

2．1 模态分析

在约束状态下，对箱体的模态进行研究。本文利用Nastran软件提供的Lanczos法对箱体进行约束状态下的模态分析，频率范围为0～2000Hz，共有113阶模态，各阶模态频率分布比较密集，这里仅列举前10阶模态结果，如表1所示。

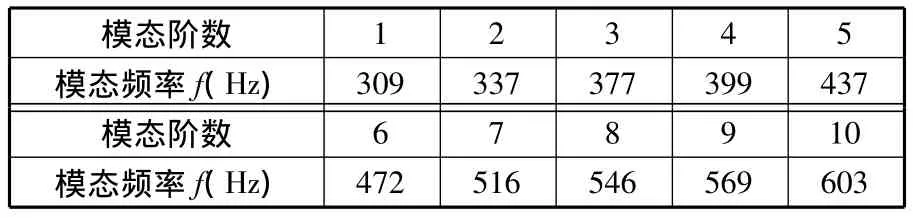
表1 箱体前10阶模态频率

2．2 静力分析

分别在7种挡位工况静态载荷作用下对箱体进行静力有限元分析，得到箱体的变形和应力情形，经分析可知，倒挡(－1挡)工况下静态变形和应力最大，图3为其箱体结构应力值大于15MPa和变形位移大于0.1mm时的变形和应力云图。

图3 箱体静力分析结果

由图3可知，倒挡工况下箱体最大应力为62.98MPa，位于后传动惰轮轴承座周围箱体顶部节点136 907位置，另外应力大于15MPa的位置还有箱体内几处轴承座孔处;箱体最大变形位移为0.5451mm，位于后传动惰轮轴承座周围箱体顶部节点136 887处，另外位移大于0.1mm的位置还有箱体顶部观察孔周围、箱体内后传动中间筋板三轴孔间位置以及前盖内部筋板处。分别对7个挡位工况进行分析，将各工况的最大变形和应力状况列于表2，由表2可知，该箱体结构设计偏于保守，有对其进行进一步优化设计的必要。

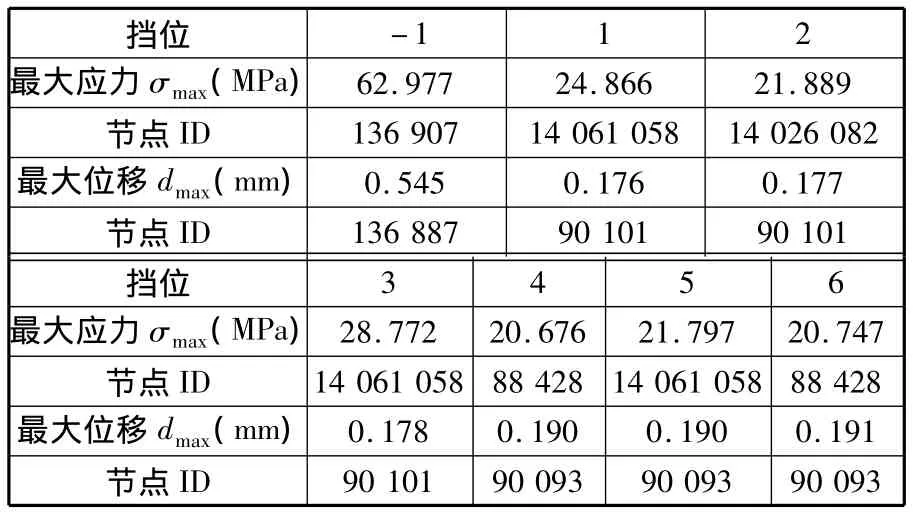
表2 箱体初始结构静力分析结果

3 箱体拓扑优化

3．1 拓扑优化基本原理

结构拓扑优化的基本思路是将寻求结构的最优拓扑问题转化为在给定的设计区域内寻求最优材料分布问题进行求解，对于连续体结构拓扑优化，目前比较成熟的方法有:均匀法、变密度法、渐进结构优化法等［8-9］。

变密度法是从均匀化方法发展而来的一种方法。基本思想是引入一种假想的密度值在［0，1］之间的密度可变材料，将连续结构体离散为有限元模型后，以每个单元的相对密度作为设计变量，将结构的拓扑优化问题转化为单元材料的最优分布问题。变密度法的拓扑优化结果是密度等值分布图，其中间密度对应的区域是假想的人工材料，在实际工程中无法实现，但是可以利用拓扑优化结果对这些区域进行人为处理，以适应实际的工程需要。

本文基于optistruct平台，采用变密度法进行变速箱箱体结构的拓扑优化，以箱体的一阶固有频率最大为目标，考虑多工况下结构的某些节点位移、全局应力、体积比分数约束，其拓扑优化的数学模型为

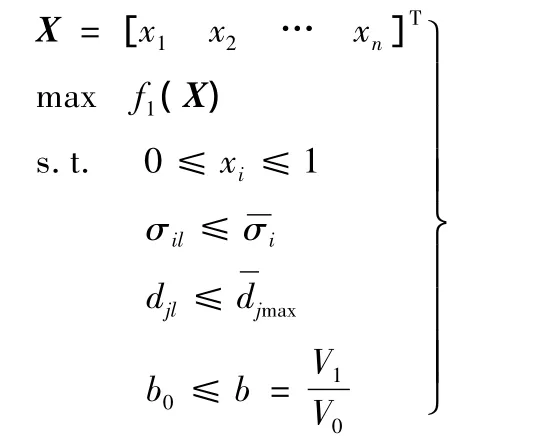
式中，f1(X)为结构第一阶固有频率;X为结构拓扑设计向量;xi为第i单元的相对密度值;σil为l工况下第i个单元应力值;σi为第i个单元许用应力值;djl为l工况下第j个节点位移值;djmax为第j个节点允许位移最大值;V1为优化后结构体积;V0为初始结构体积;b为优化后材料体积比密度值;b0为给定的保留材料体积比。

3．2 箱体结构的拓扑优化设计

箱体结构拓扑优化的目的是寻求结构的最优材料分布和最佳传力路径，所以设计空间越充分，得到的结果就越好。由于每种工况受载形式的不同，因此材料分布和载荷传递方式也不同，必须综合考虑所有工况来对该箱体结构进行综合拓扑优化，才能得到合乎实际的拓扑优化结果。

进行拓扑优化时需要定义相关优化参数，其中设计空间为模型中除去与rbe2和rbe3单元相关联的实体单元后的所有单元，设计变量为这些设计空间内单元的相对密度值，约束条件主要考虑7种载荷工况下的所有单元应力约束、某些关键节点的位移约束以及体积比分数约束，表3所示为节点位移约束，模型所有节点应力上限值为100MPa，另外设定箱体的体积比分数下限为0.6，即至少保留原模型总体积的60%;目标函数为最大化结构的第一阶固有频率，即结构最小柔度设计准则，保证结构在静载荷作用下发挥最大的承载能力。

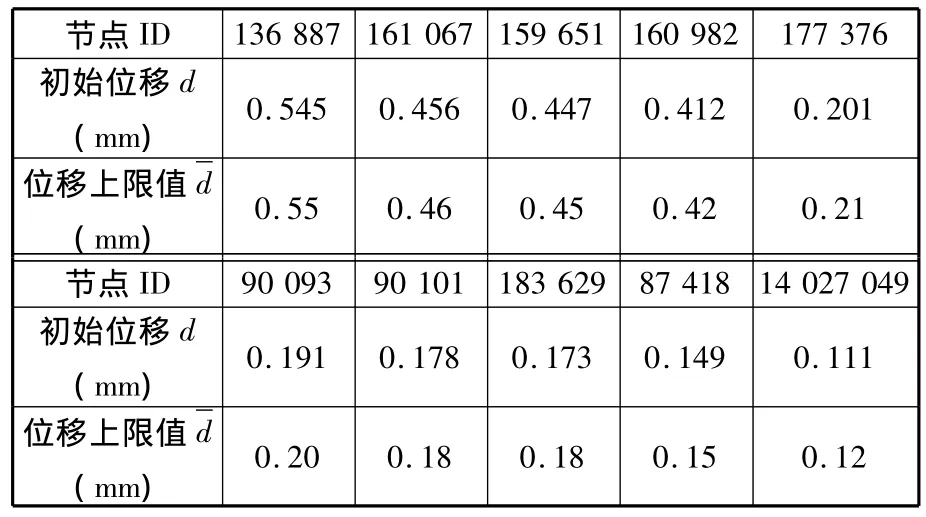
表3 拓扑优化节点位移约束

经过40次优化迭代后结果收敛，相应的结构件的第一阶模态频率、结构体积比以及约束节点177 376的位移幅值响应随迭代次数的变化关系见图4。由图4可见，整个结构件在满足动力学特性的前提下，体积比和模态频率趋于稳定，最终体积比为0.7。经过对结构件的拓扑优化，结构件的第一阶模态频率增为381Hz，相比原始结构增加了22.9%，基本满足要求。

箱体结构迭代后的最终拓扑优化结果如图5所示，其中深颜色区域为可去除大部分材料，浅颜色区域为结构需保留区域，其他颜色区域为中间区域，这些区域可去除部分材料。

根据箱体的拓扑优化结果对原始结构进行单元删减，删减部位主要位于箱体外部Ⅰ轴右侧轴承座及上部棱角处、右端盖下方棱角处、前传动箱底部筋板、箱体内部前后传动隔板右侧以及前传动中间筋板下侧等，箱体某些重要部位修改前后形状如图6所示。修改后的箱体结构质量较原先结构减小19kg，减重约4.5%。

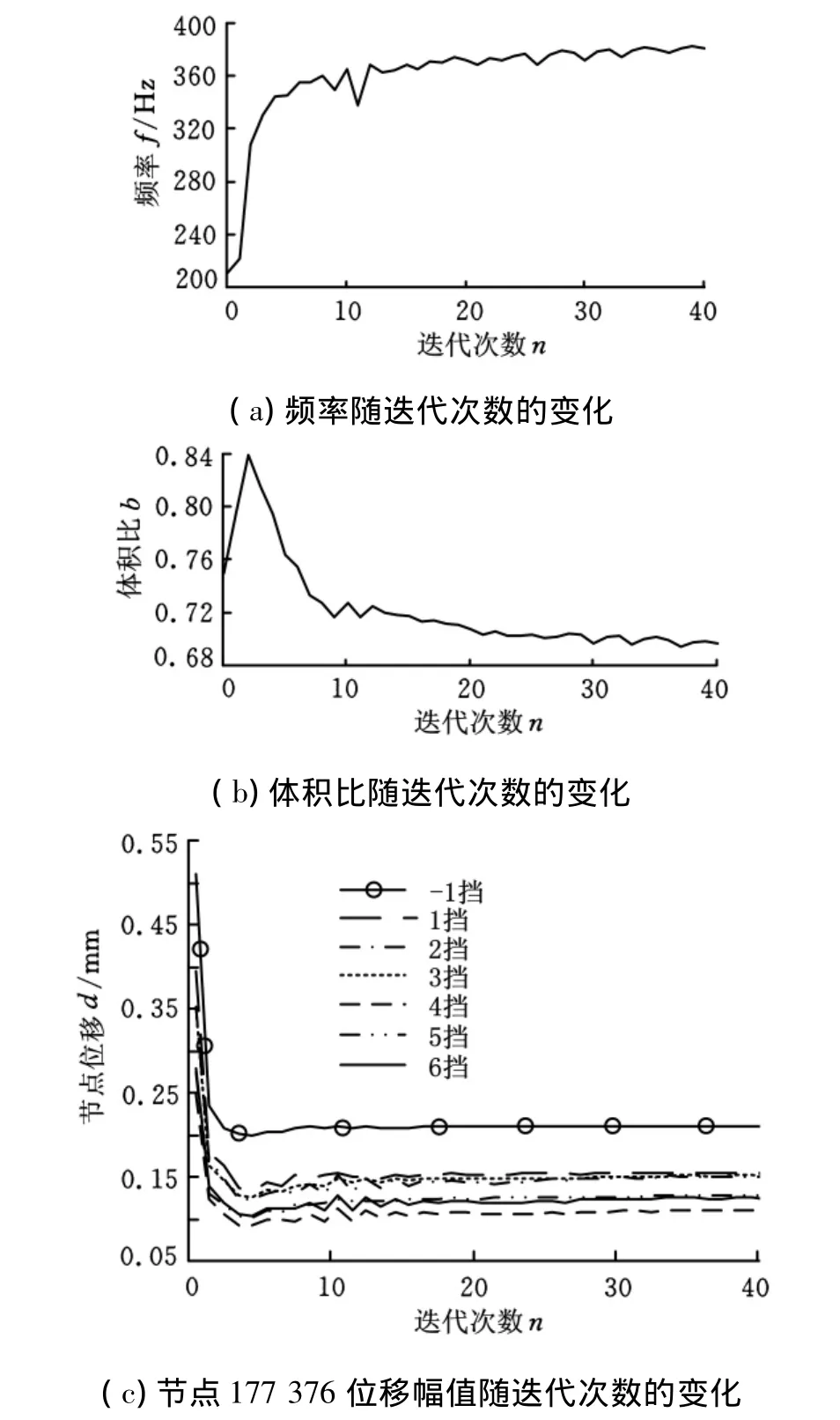
图4 箱体拓扑优化迭代过程

图5 箱体拓扑优化结果

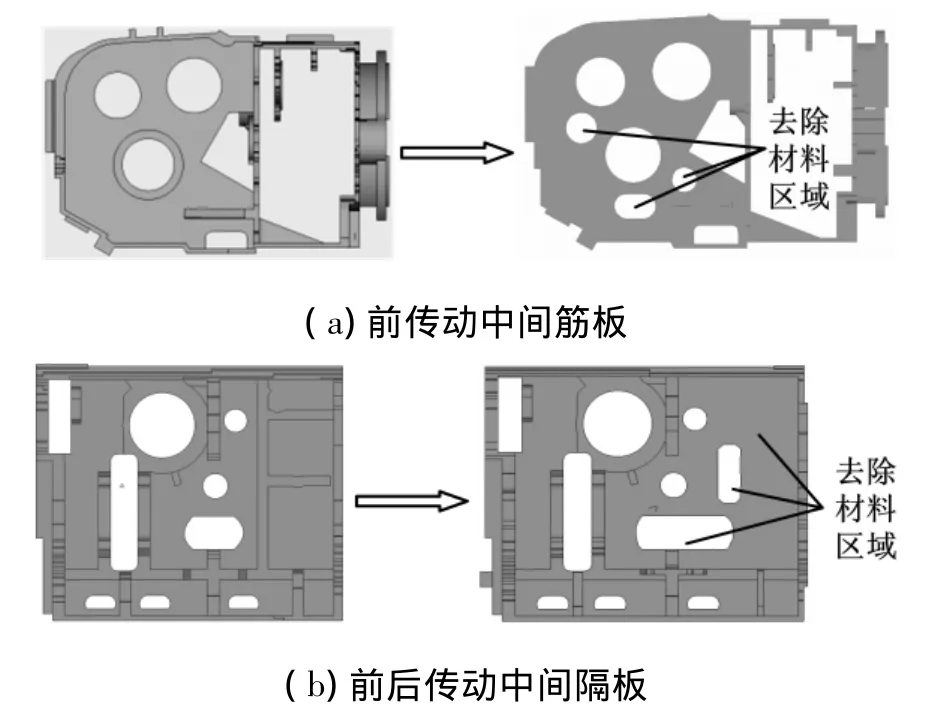
图6 箱体修改前后形状对比

为了验证改进后箱体结构的合理性，再对其进行各工况下的静力分析，分析结果如表4所示，由表可知改进后结构最大应力、位移节点位置大致不变，数值也变化不大，而且结构的第一阶固有频率为317Hz，略高于初始设计，由此可证明本文在箱体结构拓扑优化基础上对结构的改进设计是完全合理的，可以将此修改用于箱体结构的二次设计。

表4 改进后箱体静力分析结果

4 结论

(1)通过对变速箱箱体结构的有限元静力分析和模态分析，得到各载荷工况的应力和位移云图，对结构的强度、刚度及动力学特性进行评价，分析表明箱体原始设计比较保守，有进行结构优化设计的必要。

(2)对箱体初始结构进行拓扑优化设计，依据材料的分布状况进一步对结构进行局部修改设计，修改后箱体质量减小19kg，起到了一定的减重效果。同时对改进后的箱体结构进行各载荷工况再分析，分析表明对该结构的拓扑优化设计及其改进设计是完全合理的，可将其用于结构的二次设计中。

［1］ 王显会，许刚，李守成，等．特种车辆车架结构拓扑化设计研究［J］．兵工学报，2007，28(8):903-908．

［2］ 潘锋，朱平，孟瑾．微型货车车架的拓扑优化设计［J］．机械设计与研究，2008，24(2):87-90．

［3］ 龙凯，左正兴．基于拓扑优化和形状优化方法的主轴承盖结构设计［J］．农业机械学报，2008，39(4):152-156．

［4］ Lin C Y，Chao L S．Constant Weight Fully Stressed Methods for Topological Design of Continuum Structures［J］．Computer Methods in Applied Mechanicsand Engineering，2001，190(51/52):6867-6879．

［5］ 李志鑫，李小清，陈学东，等．基于频率约束的连续体拓扑优化方法的研究［J］．华中科技大学学报(自然科学版)，2008，36(2):5-8．

［6］ Fukushima J．Shape and Topology Optimization of a Car Body with Multiple Loading Conditions［J］．SAE Paper，1992，920777．

［7］ 杨志军，吴晓明，陈塑寰，等．多工况约束下客车顶棚拓扑优化［J］．吉林大学学报(工学版)，2008，36:12-15．

［8］ Bendsoe M P．Optimization of Structural Topology，Shape and Material［M］．Berlin:Springer－ Verlag Berlin Heidelberg，1995．

［9］ 周克民，李俊峰，李霞．结构拓扑优化研究方法综述［J］．力学进展，2005，35(1):69-76．