基于泛函的制冷压缩机通用涡旋型线几何理论研究

张贤明 陈国强 王立存，2 牟 瑛 陈 彬

1．重庆工商大学废油资源化技术与装备教育部工程研究中心，重庆，400067 2．西安交通大学流体机械及压缩机国家工程研究中心，西安，710049

0 引言

涡旋压缩机是基于容积变化来实现对气体压缩的流体机械，它具有结构简单紧凑、高效节能、微震低噪声以及可靠性高等一系列的优点，使得涡旋压缩机在制冷和空调领域的应用有着飞速的发展，并且有在更大范围应用的趋势。涡旋压缩机的核心技术是动静涡旋盘的涡旋型线形状设计［1］。目前涡旋压缩机型线一般是利用圆的渐开线以及其修正曲线。它们的几何性质较简单，在加工工艺过程上较为方便。然而，包括圆的渐开线在内的传统单一型线，其几何特性和数学模型存在一定局限性。基于以上缘故，本文提出基于泛函的通用涡旋型线理论，即根据平面曲线弧微分固有方程理论［2－3］和 Tayl or级数思想，任意函数曲线的数学表达式都可以将其展开为切向角参数φ的级数的弧函数形式。它包含了所有单一型线的优点，可在不同场合运用优化的思想得到综合各目标函数最佳的型线方程，本文就通用涡旋型线几何理论进行了研究推导。

1 涡旋型线向量形式分析

1．1 节线方程

文献［4-6］已经证明控制方程Rg＝d Rs／dφ是对于任意曲线耦合的控制方程。它是涡旋型线耦合的必要条件，而非充分条件。如图1所示P向量的位置方程为

其中，Rs与Rg垂直且Rg＝d Rs／dφ。由此得到其节线方程亦即得到任意一条型线方程：

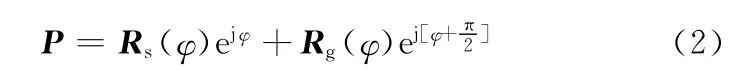
图1 曲线方程沿其切向和法向的分解

由节线方程得到有厚度的内外涡旋型线：

式中，t为涡旋型线的厚度。

动涡盘型线P′是通过静涡盘型线P沿旋转180°角，再在θ方向平移Ror得到。

1．2 曲率及曲率半径

根据节线方程可得曲率以及曲率半径［7］：

同理有

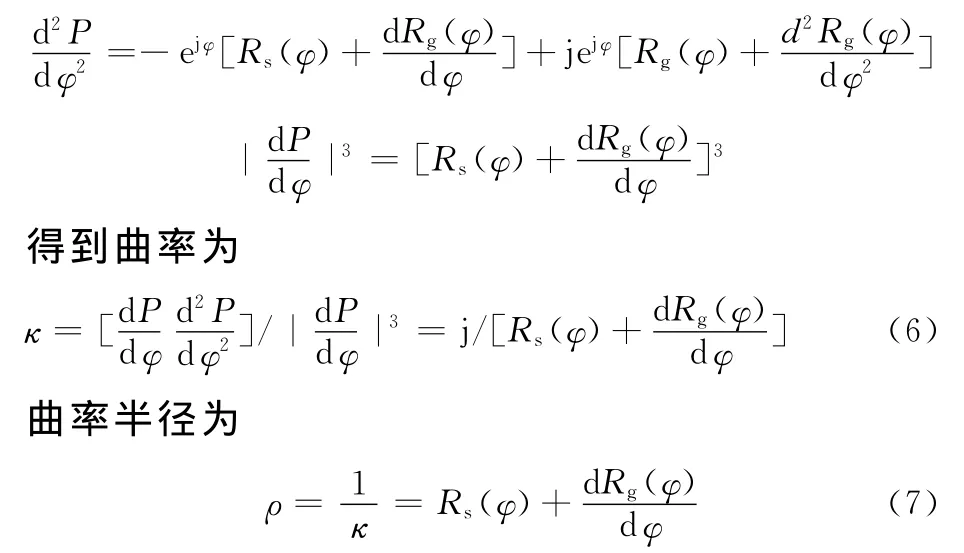
同理有Po、Pi的曲率半径为

当曲率半径的倒数大于零，即ρ′＞0，则可形成涡旋型线。

1．3 直角坐标下的坐标表示

直角坐标下的坐标表示如下：

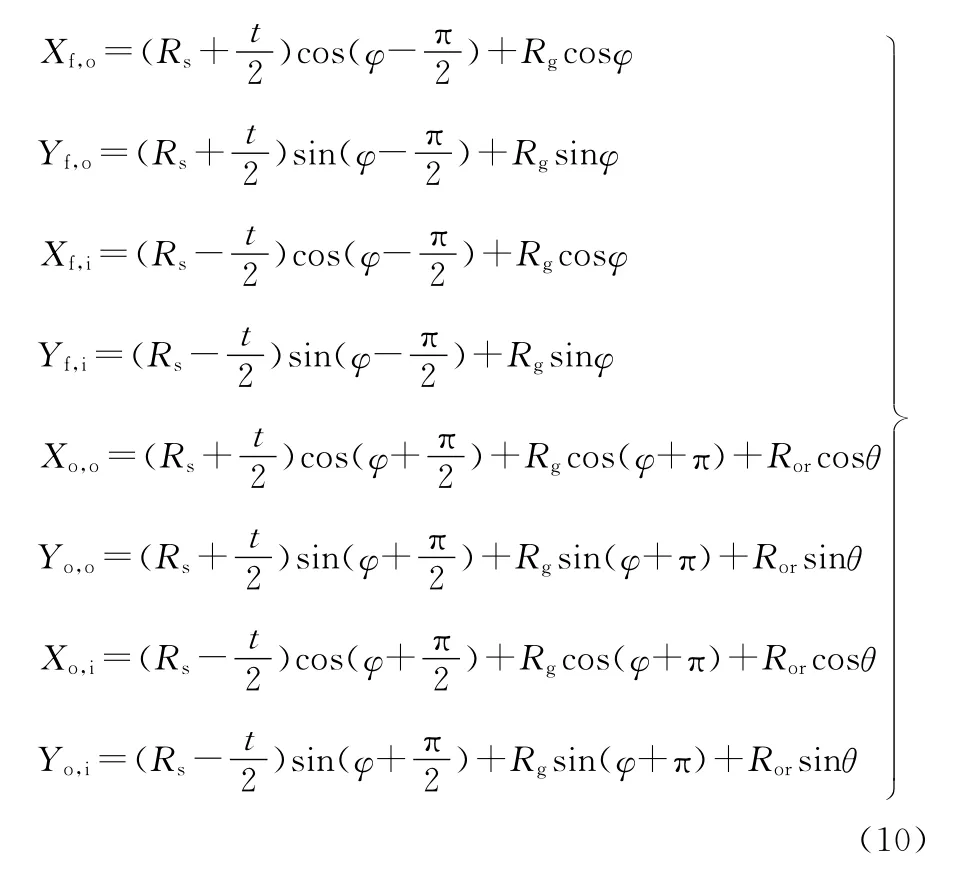
式中，t为厚度，它是关于φ的函数；θ为公转角度；Ror为动静涡盘的公转半径。

1．4 型线线长

型线线长为

2 涡旋型线泛函表征分析

2．1 基于泛函理论的涡旋型线

涡旋型线是由几何共扼型线构成的，根据平面曲线弧微分固有方程理论［4-5］和Taylor级数思想，任意函数曲线的数学表达式都可以将其展开为切向角参数φ的级数的弧函数形式；反之，只要曲率半径ρ（φ）是关于切向角参数φ的递增函数，均可通过切向角参数φ的级数的弧函数形式来表征任意共扼函数曲线。同时，三角函数、指数函数、对数函数等均可用幂级数函数来表达［8-9］。根据现有涡旋型线的级数表达形式的共有特性构成的共扼曲线可表达为函数类的级数形式［10］：

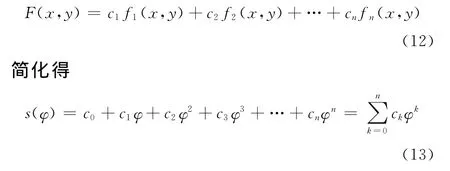
式中，c0，c1，…，cn均为涡旋型线的系数；s（φ）涡旋型线方程的弧度函数。

与上述涡旋型线的向量表示类似，基于涡旋型线的几何性质，其曲率半径、线长分别为

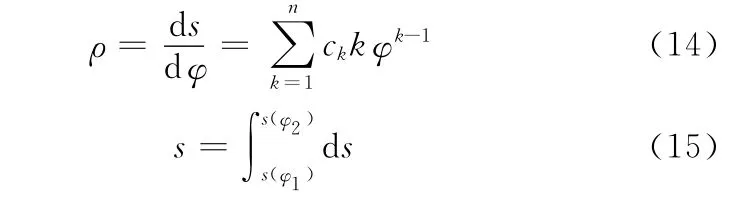
结合向量形式的涡旋型线可得

2．2 t与R or之间的关系

当任意一对共轭点接触时，两涡盘的中心距离为一常量，圆周公转平动半径为Ror，如图2所示，即将两个涡旋盘中心重合放置在一起，任意一对共轭点在垂直于相应表面的方向上相距为Ror。此时，t与Ror之间的关系为

图2 t与R or之间关系图

2．3 行程容积A p

对通用涡旋型线集成型线涡旋压缩机而言，其压缩比和体积利用系数是非常重要的性能指标，它们对提高压缩性能和对整个空压系统工作性能的影响关系较大。所以行程容积的计算是至关重要的。在实际中，动静涡盘是有厚度的，我们设厚度为t。通过节线方程平移的原则沿节线法向平移t／2距离得到型线动静涡盘型线方程。于是可求出动静涡盘内外型线围成的区域面积（图3）［10-12］。

图3 动静涡盘形成动态压缩腔

月牙形动态压缩腔面积（图4）为

图4 静涡盘与动涡盘所围面积域

由此可得

3 通用涡旋型线举例

当k＝3，公转半径Ror＝2 mm，大盘半径R＝40 mm的情况下研究其涡旋型线的几何特性。

3．1 型线方程及线长

型线线长为

3．2 直角坐标系下表征

由几何特性知：

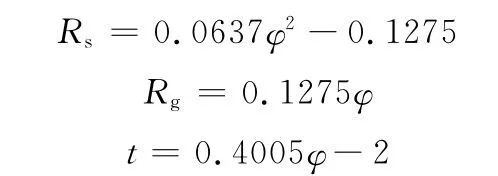
则有其涡旋型线直角坐标表征为

涡旋型线形状如图5所示。

图5 涡旋型线形状

3．3 行程容积与压缩比及涡旋盘的利用率

通过MATLAB编程计算可得此涡旋型线行程容积与压缩比。

4 结论

（1）针对单一涡旋型线受其固定数学模型固有特性的限制，提出基于泛函的通用涡旋型线形式设计思路。基于泛函的通用涡旋型线是所有涡旋型线类型的集合，是涡旋型线设计的新思路。

（2）本文就基于泛函的通用型线形式，从控制方程入手，结合泰勒级数思想，在笛卡尔直角坐标系下，讨论研究了其曲率半径、行程容积、型线线长的特性；涡旋型线厚度t变化，公转半径Ror与型线方程之间的关系，以及在直角坐标系下涡旋型线的表示。

（3）举例说明了基于泛函理论的通用涡旋型线几何特性。基于泛函的通用涡旋型线的研究为涡旋压缩机型线设计拓宽了思路。

［1］ 李连生．涡旋压缩机［M］．北京：机械工业出版社，1998．

［2］ 王立存，陈进，李世六，等．基于泛函的涡旋型线共轭啮合理论［J］．机械工程学报，2006，43（3）：49－53．

［3］ 陈进，王立存，李世六．通用涡旋型线理论研究与深入分析［J］．机械工程学报，2006，42（5）：11－15．

［4］ 樊灵，屈宗长，勒春梅，等．涡旋压缩机通用型线设计的现状和进展［J］．流体机械，2000，28（1）：27：30．

［5］ 樊灵，屈宗长，勒春梅．涡旋压缩机型线研究的概述［J］．机械工程学报，2000，36（9）：1－4．

［6］ 王立存，陈进．涡旋压缩机通用涡旋型线控制方程的必要性研究［J］．中国机械工程，2008，19（10）：1233－1236．

［7］ 屈宗长，樊灵，王笛生，等．通用型线涡旋压缩机的几何理论［J］．西安交通大学学报，1999，33（11）：39－42．

［8］ Gravesen J，Christian H．The Geometry of the Scroll Co mpressor［J］．Sian Review，2001，43（1）：113－126．

［9］ Wang Licun，Chen Jin．Inherent Engagement Mechanism Study of Profile of Scroll［C］／／Proceedings of International Mechanical and Infor mation Technology．Chongqing：SPIE，2005：60400I6－6．

［10］ 杨启超，赵远扬，李连生，等．涡旋压缩机几何模型研究［J］．中国机械工程，2007，18（3）：257－259．

［11］ Tseng Chin－Huan，Chang Yu－Choung．Family Design of Scroll Co mpressors wit h Opti mization［J］．Applied Ther mal Engineering，2006，26（10）：1074－1086．

［12］ Aprea C，Mastrullo R，Renno C．Experimental A－nalysis of the Scroll Co mpressor Perfor mances Varying Itsspeed［J］．Applied Ther mal Engineering，2006，26（10）：983－992．