平板微通道流动入口段粗糙度效应的数值模拟

高新学 云和明

1.山东省交通工程监理咨询公司，济南，250014 2.山东建筑大学，济南，250101

0 引言

微细尺度通道内的流动在超大规模集成电路的冷却、航天技术中的对热环境控制及生物医学中的细胞分离等方面有广泛的应用。目前，国内外微通道内流动特性的实验结果还存在许多定性和定量的矛盾，造成该问题的一个很重要的原因来自于壁面粗糙度对流动特性的影响。

Nikuradse[1]认为，层流条件下粗糙表面的影响在相对粗糙度小于5%时可以忽略。微尺度条件下，实验已经发现不同于常规尺度下的阻力特性，故需要深刻认识粗糙表面对微流动阻力的影响。Mala等[2－3]提出粗糙度黏度的概念来解释阻力的提高，而Sabry等[4]则通过附壁气层的假说解释了微尺度流动中阻力的特殊现象。一些学者通过规则的突起来模拟粗糙元，并用数值方法初步分析了微细通道的流动和传热特性[5－13]。范小苗等[14]采用多孔介质模拟粗糙元，对不同雷诺数及截面尺寸下方形直管微通道的流动进行了数值模拟研究。Liu等[15]基于Lattice－Boltzmann方法研究了分形粗糙度对微泊松流动的影响规律。张春平等[16－17]分别通过实验和求解粗糙度的摄动方程的方法，研究了粗糙度对微通道流动传热的影响规律。闻劭意等[18]则用规则微小横肋模拟固体表面粗糙度，模拟和分析了粗糙元间的局部流动和换热特性。

综上所述，采用CFD研究粗糙度对微通道流动的影响不但可以避免分子动力学的大量计算，还能比较切合实际地反映微通道流动的规律。为探究粗糙度对平板微通道的流动和传热的影响机理，本文通过建立粗糙元的方法，利用CFD数值模拟了粗糙元的高度和流体的速度对平行平板微通道入口段流动特性的影响规律。

1 几何模型及求解方法

三角形锯齿状粗糙元模型如图1所示，粗糙元的高度为h。本节建立了数个三角形锯齿状的粗糙元模型，通道的长度为10mm，平板通道间的距离D＝0.1mm，三角形粗糙元的底边恒定为10μm，粗糙元的高度分别为 1μm、2μm、3μm、5μm、8μm和15μm。三角形锯齿状粗糙元的特点是三角形粗糙元紧密相连，其间无间隙。若材料表面的粗糙元分布均匀且排列紧密，那么就可以利用三角形锯齿状粗糙元模型来研究粗糙元对平行平板微通道流动和传热的影响。选择水为流体，流体从左侧流进，右侧流出。

采用CFD技术对微通道稳态的流动进行了模拟。计算过程中采用有限容积法离散方程，同时求解流体的连续性方程、动量方程和能量方程。网格为非结构网格，贴近壁面处采用局部加密处理，为节省计算机的内存，对计算工况进行了网格无关性检验。选用二维不可压缩流动计算模型，流体的物理性质随温度的变化而变化，忽略黏性耗散和流体的轴向导热。在微通道的进出口分别设定速度进口边界条件和压力出口边界条件。流态选取层流和紊流，其中，为提高紊流的计算精度，选用雷诺应力紊流模型。动量方程的对流和扩散项采用Quick格式进行离散，采用SIMPLER方法计算压力和速度的耦合。当能量方程中的收敛残差小于10－6时，整个计算过程被认为收敛。

图1 三角形锯齿状粗糙元平板微通道模型

2 求解结果及讨论

2.1 速度对水力入口段长度的影响

图2、图3是平板微通道在粗糙元高度为1μm时不同速度条件下流动入口段的速度等值线图，根据速度等值线可有效判断不同条件下的流动入口段长度。根据流体力学的流动边界层理论，流动在边界层达到充分发展段前，流体沿垂直于流动方向的速度剖面的分布沿程不断变化，在流动进入充分发展段后，流体的速度剖面的分布沿程将不再变化。根据充分发展段过流断面的速度分布保持不变的特点，获得粗糙元高度为1μm时，不同速度条件下平板微通道的流动入口段长度，如表1所示。

表1 粗糙元高度为1μm时，不同速度条件下平板微通道的流动入口段长度

图4是平板微通道进口平均流速与流动入口段长度的关联图。根据图4和表1可以看出，随着流速的增大，平板微通道的水力入口段长度呈现先增大后减小的趋势，最终当流动进入湍流状态时，流动入口段的长度也趋于稳定。根据Guo等[19]提出的场协同理论，流体的速度场和温度场是耦合的，流体速度场的变化同样引起其温度场的变化，进而影响流体的对流换热，所以粗糙元高度一定时，不同速度条件下平行平板微通道充分发展流动入口段的长度不同，可导致不同速度条件下平板微通道内流体的对流传热效果的不同。

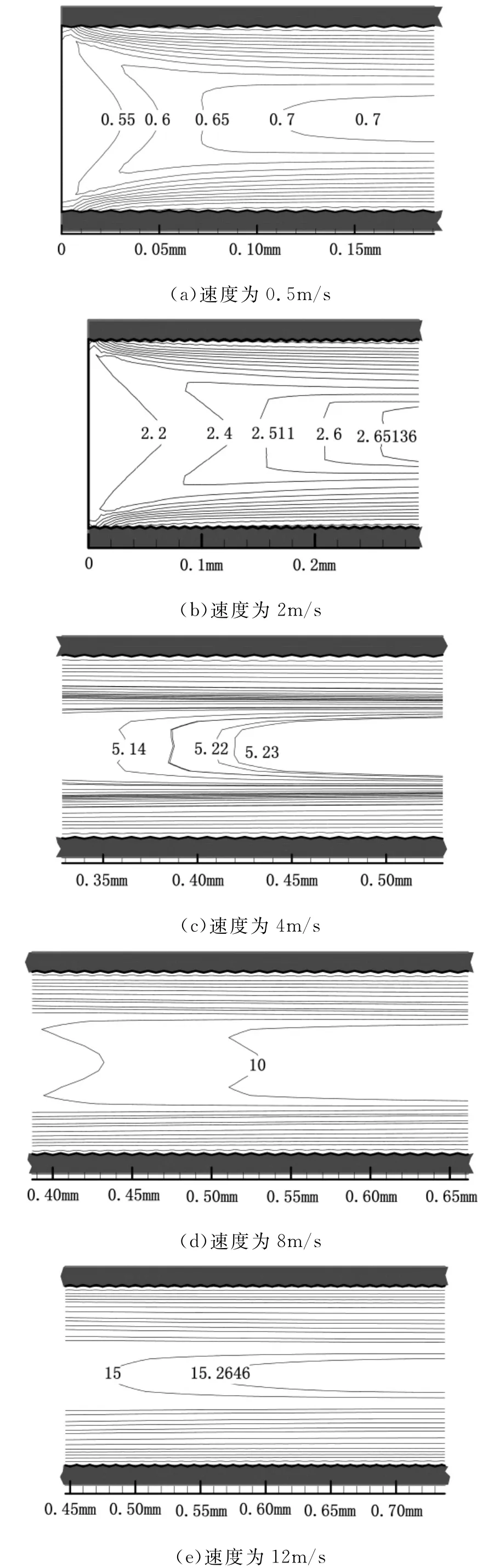
图2 粗糙元高度为1μm、不同速度下平板微通道流动入口段的速度（m／s）等值线图（速度为0.5～12m／s）

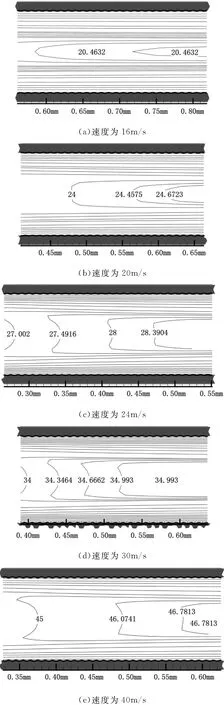
图3 粗糙元高度为1μm、不同速度下平板微通道流动入口段的速度（m／s）等值线图（速度为16～40m／s）

图4 平板微通道进口平均流速与流动入口段长度的关系

2.2 粗糙元高度对水力入口段长度的影响

由图5～图7可以看出，当粗糙元高度分别为1μm、2μm、3μm时，通道的入口段长度分别为260μm、450μm、440μm；但当粗糙元高度大于3μm时，通道的入口段长度随着粗糙元高度的增加而增大，在粗糙元高度为8μm时，通道的入口段长度达到最大值500μm；接下来随着粗糙元的高度的增加，通道入口段长度随之变小，在粗糙元高度为200μm时达到最小（所研究范围内），为220μm。

图5 流度为2m／s、不同粗糙元高度下平板微通道流动入口段的速度（m／s）等值线图（粗糙元高度为1～3μm）

图6 流度为2m／s、不同粗糙元高度下平板微通道流动入口段的速度（m／s）等值线图（粗糙元高度为5～20μm）

图7 绝对粗糙度同流动入口段长度的关联图

图7所示为平板微通道进口平均流速一定条件下粗糙元高度对流动入口段的影响。由图5可以看出，对于特定的通道，在流体进口平均流速恒定条件下，随着粗糙元高度的增大，流动入口段长度强非线性变化，从而导致粗糙元高度不同时，平板微通道内流体对流传热效果的差别较大。由此可推断，微通道表面粗糙元的高度、形状和分布可能是微通道对流换热实验结果至今仍然不一致的真正原因。

2.3 相对粗糙度对流动特性的影响

如图8所示，随着相对粗糙度ε的增大，平行平板微通道的阻力因数逐渐增大，且相对粗糙度为1%时已经偏离常规的理论值，从而说明相对粗糙度超过1%时，对于微通道来说，已经不能忽略其影响；此外随着相对粗糙度的增大，平板微通道层流向紊流转变的转捩雷诺数提前，这可能是Peng等[20－21]在微通道实验发现转捩雷诺数提前的真正原因。

图8 相对粗糙度时阻力因数f与雷诺数Re的关系

2.4 速度对压降特性的影响

如图9所示，随着粗糙元高度的增大，平行平板微通道的压降逐渐增大，且当粗糙元高度大于5μm时，粗糙元高度越大，平板微通道的压降越大。当粗糙元高度为15μm、速度为20m／s时，压降为17.1MPa；而当粗糙元高度为1μm、速度为20m／s时，压降为1.53MPa。

3 结论

（1）对于特定通道，在粗糙元高度一定条件下，随着速度的增加，平板微通道水力入口段长度先增大后减小，最终流动进入湍流状态时，流动入口段的长度也趋于稳定。

图9 不同粗糙元高度下速度同压降的关联图

（2）随着粗糙元高度的增加，水力入口段长度呈现不稳定的变化规律。

（3）随着粗糙元高度增大，平行平板微通道的阻力逐渐增大，且相对粗糙度为1%时已经偏离常规理论值，从而说明相对粗糙度超过1%时，对于微通道来说已经不能忽略其影响。此外，随着相对粗糙度的增加，平板微通道层流向紊流转变的转捩雷诺数提前。

[1]Nikuradse J.粗糙管中的水流的规律[M]，张瑞瑾，译，北京：水利出版社，1957.

[2]Mala G M，Li D，Dale J D.Heat Transfer and Fluid Flow in Microchannels[J].International Journal of Heat and Mass Transfer，1997，40（13）：3079-3088.

[3]Mala G M，Li D，Werner C，et al.Flow Characteristics of Water Through a Microchannel Between Two Parallel Plates with Electrokinetic Effects[J].International Journal of Heat and Fluid Flow，1997，18（5）：489－496.

[4]Sabry M N，Mansoura U.Scale Effects on Fluid Flow and Heat Transfer in Microchannels[J].IEEE Transactions on Components and Packaging Technologies，2000，23 （3）：562－567.

[5]Giulio Croce，Paola D’Agaro.Numerical Analysis of Roughness Effect on Microtube Heat Transfer[J].Superlattices and Microstructure，2004，35 （3／6）：601－616.

[6]Wang H，Wang Y.Influence of Three－dimensional Wall Roughness on the Laminar Flow in Microtube[J].International Journal of Heat and Fluid Flow，2007，28（2）：220－228.

[7]Valdés J R，Miana M J，Pelegay J L，et al.Numerical Investigation of the Influence of Roughness on the Laminar Incompressible Fluid Flow through Annular Microchannels[J].International Journal of Heat and Mass Transfer，2007，50（9／10）：1865－1878.

[8]Khadem M H，Shams M，Hossainpour S.Numerical Simulation of Roughness Effects on Flow and Heat Transfer in Microchannels at Slip Flow Regime[J].International Communications in Heat and Mass Transfer，2009，36（1）：69－77.

[9]杜东兴.可压缩性及粗糙度对微细管内流动及换热特性的影响[D].北京：清华大学，2000.

[10]王爱国，冯妍卉，林林，等.三角形粗糙元的微通道内流动换热的模拟分析[J].热科学与技术，2008，7（1）：11－16.

[11]张程宾，陈永平，施明恒，等.表面粗糙度的分形特征及其对微通道内层流流动的影响[J].物理学报，2009，58（10）：7050－7056.

[12]陈建华，张会强，张贵田.含人为粗糙元微小冷却通道内的流动与换热[J].清华大学学报（自然科学版），2008，48（5）：900－903.

[13]邹江，彭晓峰，颜维谋.壁面粗糙度对通道流动特性的影响[J].化工学报，2008，59（1）：25－31.

[14]范小苗，张鸿雁.壁面粗糙度对微通道流动影响的数值模拟研究[J].西安航空技术高等专科学校学报，2007，25（5）：38－40.

[15]Liu C F，Ni Y S.The Fractal Roughness Effect of Micro Poiseuille Flows Using the Lattice Boltzmann Method[J].International Journal of Engineering Science，2009，47（5／6）：660－668.

[16]张春平，唐大伟，曲伟，等.粗糙度对微细通道内流动特性影响的实验研究[J].上海理工大学学报，2008，30（1）：55－58.

[17]张春平，唐大伟，韩鹏，等.粗糙度对微细圆管内流动特性影响的摄动分析[J].工程热物理学报，2008，29（5）：849－853.

[18]闻劭意，彭晓峰，吴海玲，等.粗糙表面不同粗糙元间局部流动与传热特性[J].化工学报，2005，56（3）：408－411.

[19]Guo Z Y，Wang S.Novel Concept and Approaches of Heat Transfer Enhancement[C]／／Proceedings of Symposium on Energy Engineering in the 21st Century（SEE2000）.New York，2000：118－126.

[20]Peng X F，Peterson G P.Convective Heat Transfer and Flow Friction in Microchannel Structures[J].International Journal of Heat Mass Transfer，1996，39（12）：2599－2608.

[21]Peng X F，Peterson G P.The Effect of Thermofluid and Geometrical Parameters on Convection of Liquids through Rectangular Microchannels[J].International Journal of Heat and Mass Transfer，1995，38（4）：755－758.