贵州马尾松单株木二元材种出材率表的编制

金 明，丁贵杰

（贵州大学 造林生态研究所，贵州 贵阳 550025）

马尾松Pinus massoniana是中国主要用材树种之一，其用材林和人工林面积分别占全国的16.6%和16.9%。在贵州马尾松的面积和蓄积已分别占到乔木林的26.95%和36.10%[1]。研究和编制马尾松材种出材率表在指导生产实践和森林资产评估等方面具有重要意义。21世纪初，马尾松材种出材率表的研究受到一些学者的重视。江希钿等[2]使用改进的Demearschalk削度方程对马尾松干形进行了研究，随后又做了马尾松二元材种出材率表的编制研究[3]，但并未应用其之前进行的削度方程研究成果，而仅使用材积比方程。同年，林剑峰[4]和王鹏程等[5]也做了类似研究，前者仍采用材积比方程编表，后者则采用削度-材积系统编表。本研究采用类似削度-材积系统的编表方式，在建立削度方程、累积材积方程和树皮材积方程基础上，编制二元材种出材率表。

1 建模及编表资料

共使用406株解析木（下文简称 “样木”）数据，其中26 cm径阶以下样木来自贵州省龙里林场，28～66 cm径阶样木来自贵州省第3次森林资源规划设计调查（由贵州省林业调查规划设计院提供）。全部样木来自贵州29个县区，分属贵阳、安顺、六盘水、毕节、遵义、铜仁、黔南和黔东南等8个地市。来源地以黔南和黔东南为主，分别占总株数的53.7%和31.8%。

来自龙里林场的解析木共163株。每株样木数据包括树干全高（H）和11个分别位于1.3 m，0～9/10 H高处的断面的带去皮径，以及现场造材数据。另外，243株样木数据包括树干全高H和13个分别位于1.3 m，0～9/10 H，1/4 H和3/4 H高处的断面的带去皮径，无造材数据。

全部样木分布在6～66 cm共31个径阶内。其中15株的径阶21个，占径阶总数的2/3略强，低于10株的径阶6个，11～14株的径阶4个。在尽量保证各径阶建模样木满足10株的前提下，将全部样木分成2组，分别用于模型拟合和模型检验。数据详情见表1。

表1 样木数据基本统计特征Table1 Mean sample tree characteristics of Pinus massoniana

2 模型拟合与优选

2.1 拟合方法

方程的拟合在R软件[6]中实现。由功能包nlrwr[7]中的nls非线性回归函数进行拟合，并结合拟合效果诊断，适当采用boxcox.nls函数，对原方程进行Box-Cox函数转换，以削弱异方差性，且不改变原模型变量之间的关系。Box-Cox转换函数[7]表达式如下：

式（1）中： y=f（x，β），β 为模型参数， λ 为待估参数。

另外， Mak-Burkhart方程[式（2）]和 Kozak方程[式（3）]含有需在模型回归之前预先给定的常数（a1，a2和p；下文称 “特征参数”）。对此特征参数采用取值空间格网搜索的方法，以拟合残差平方和最小为准则确定。

2.2 模型优选原则

2.2.1 多指标综合比较 各模型的优选在考虑回归模型常用评价指标（剩余平方和、剩余标准差、复相关系数、修正复相关系数和信息量准则）的同时，还考察了总相对误差、平均系统误差、平均相对误差绝对值和预估精度等指标[8]。

2.2.2 进行适合性检验 对削度方程进行适合性检验，即利用检验数据，分别对各方程在指定树干5个相对位置（0.1H，0.2H，0.5H，0.8H和0.9H）的预估效果，以偏差（W），绝对偏差（|W|），相对偏差（MSD）和平均相对偏差（ME）为指标， 进行综合评分[9]比较。

2.2.3 模型优化 对模型参数拟合结果不能全部满足统计显著性要求的模型进行参数优化。

2.3 削度方程

2.3.1 试验方程 选用3个具有代表性的削度方程，分别是Demearschalk削度方程[式（2）]，Mak-Burkhart的分段削度方程[式（3）]和Kozak的可变指数削度方程[式（4）]。其形式如下：

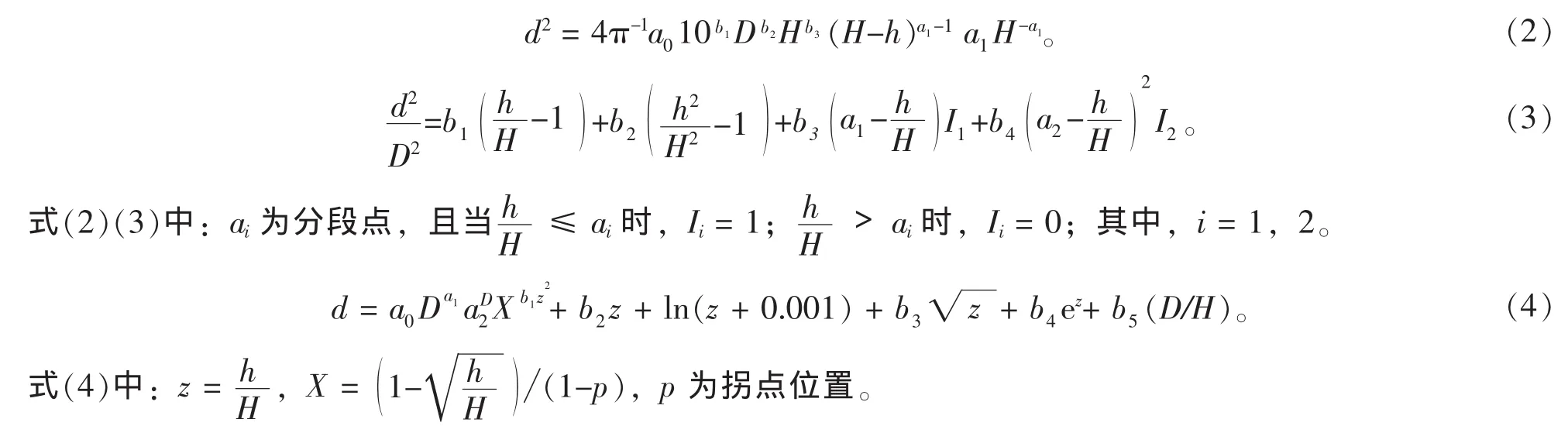
以上各式中，D为带皮胸径，H为树干全高，h为断面高度，d为h高度处断面的去皮直径，ai（i=0，1，2）和bi（i=0，1，…，5）为待估参数；径和高的单位分别为cm和m。

2.3.2 模型拟合 经预估，式（3）特征参数a1和a2分别取值0.08和0.73，式（4）特征参数p取值0.05。由于式（4）的b2参数拟合结果统计上不显著（P=0.1317），变动系数等于66.33%，需对该参数进行优化。经去除参数b2后，得到新模型（4*）：

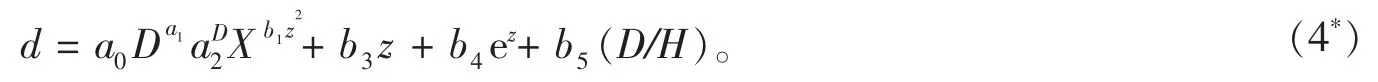
式（4*）中各符号含义同前文。用该模型取代式（4）做进一步的模型评价与比较。Demearschalk方程[式（2）]原为一致性削度方程[10]，即其积分材积与山本式材积一致。为保留其一致性，采用分步拟合的方法，即先拟合山本式材积方程的3个参数，再拟合第4个参数a1。

估计过程中， 分别对式（2）（3）（4）和（4*）进行了 Box-Cox函数转换， λ 取值均为 0.4。 经 Box-Cox函数转换后，异方差得到式一定程度的削弱，残差的正态性得到改善。各方程参数拟合结果见表2。

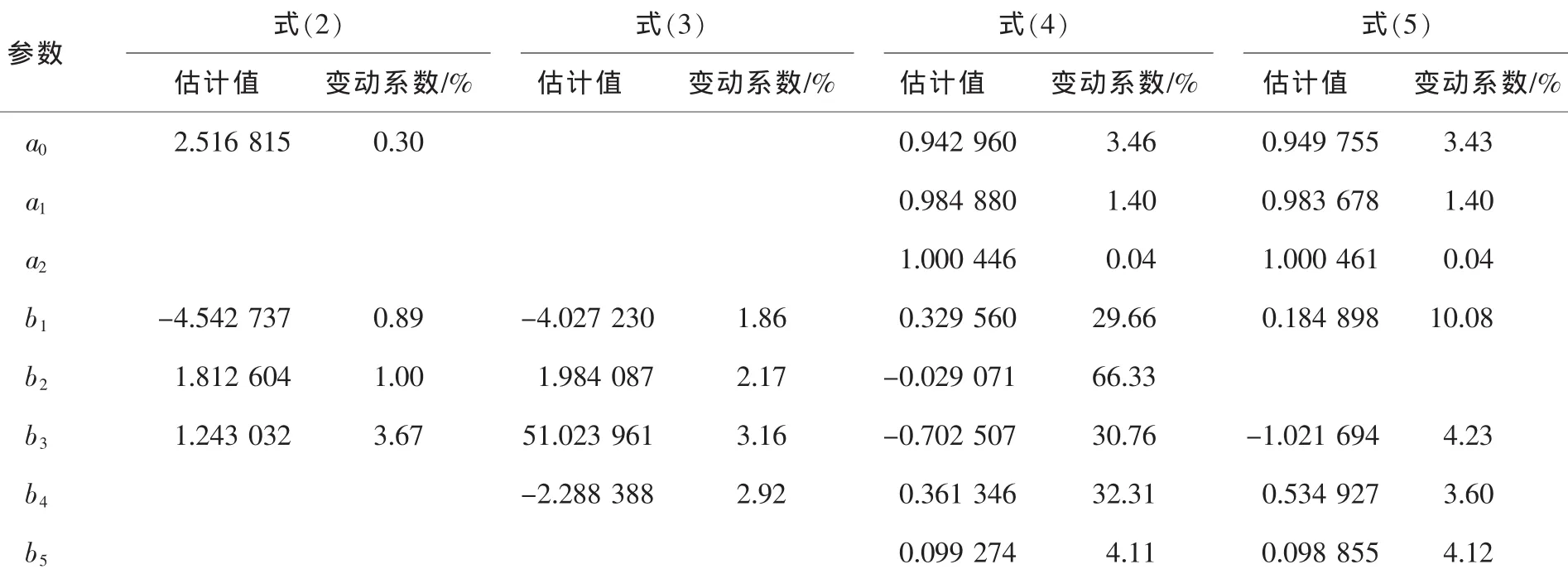
表2 削度方程参数估计结果Table2 Parameters estimation taper function models

2.3.3 模型优选 参数估计结果（表2）显示，式（2）（3）和（4*）各参数估计值的变动系数均小于11%，各参数估计值稳定性很高。参数估计的t检验也显示，全部参数在0.001水平上显著。用建模样木数据，计算并分析各统计指标（表3和表4）。由表3各统计指标计算结果可知，式（4*）最优，式（3）次之。进一步考察表4，式（4*）在整体及全部径级的平均相对误差绝对值（RMA）和预估精度（P）这2项指标上，均表现最优，在总相对误差（RS）指标上，式（4*）也表现最优。经综合分析，可以确认式（4*）最优。

另用检验数据（样木数116）对3个方程进行了适合性检验，经综合分析比较，仍以式（4*）最优。

表3 削度方程模型拟合效果评价指标Table3 Estimation indexes for regression of taper function models

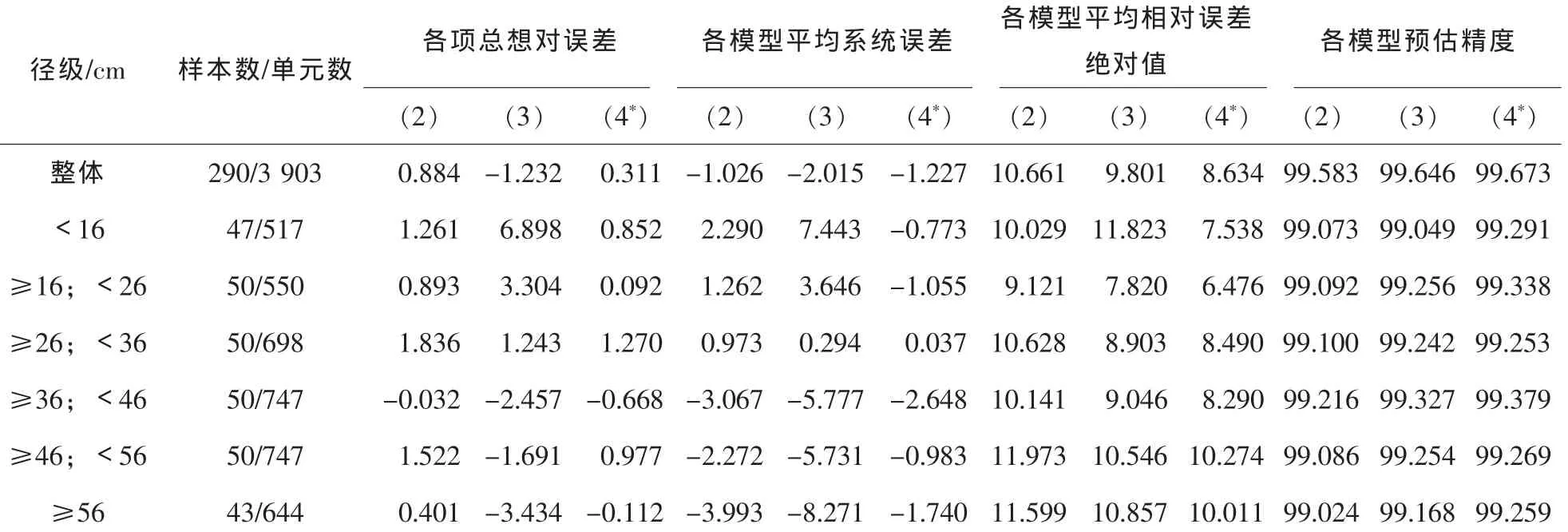
表4 削度方程模型分径级评价指标Table4 Estimation indexes calculated by diameter class for taper function models

2.4 累积材积方程

从理论上讲，削度方程沿整个树干区间的定积分即为树干材积。但通过其积分而估算的方法为间接方法，其精度需要验证。为此，以优选出的削度式（4*）的积分式为基本型。另外，构建了线性修正式（7）和幂函数修正式（8），加上山本材积式（5），组成以下4个方程，用于比较和检验：

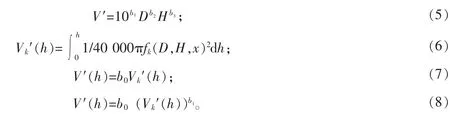
以上式（5）～（8）中，V为带皮材积，V′为去皮材积，Vk（h）为直接通过kozak方程积分而得的0～h段去皮材积，V′（h）为0～h段去皮材积，h为断面高度，fk（D，H，x）指Kozak方程高处去皮断面径的预估函数，b0和b1为待估参数。

拟合过程中所用的材积观测值用插值的方法，以Stineman函数[11]为插值函数，以1 cm为积分区间长度，对树干全长或材段区间积分求得。Eerikainen[12]曾在研究思茅松Pinus kesiya时采用类似方法。

参数估计 （表5）显示，各模型参数估计值的变动系数均处于小于4%的低水平。各参数估计的t检验也表明各方程参数均在0.001水平上显著。

经比较（表 6 和表 7）， 式（5）对全干材积的预测效果最好，式（6）和（7）表现相当， 而式（8）最差。 即便如此， 式（6）和（7）由建模样本和检验样本得出的系统误差E均小于式（5），前两者的预估精度仅比后者少0.02个百分点。就式（6）和（7）而言，对建模样本全干和材段去皮材积，前者的修正复相关系数略大于后者，而对建模样本和检验样本预估的系统误差，则后者均略低于前者，其余指标两者也基本一致。综合而言，两者相关不大。由于式 （5）不具预估材段材积的能力。而在材种出材量估算中，材段材积的预估能力居很重要地位，因此，选用式（7）作为累积材积方程。

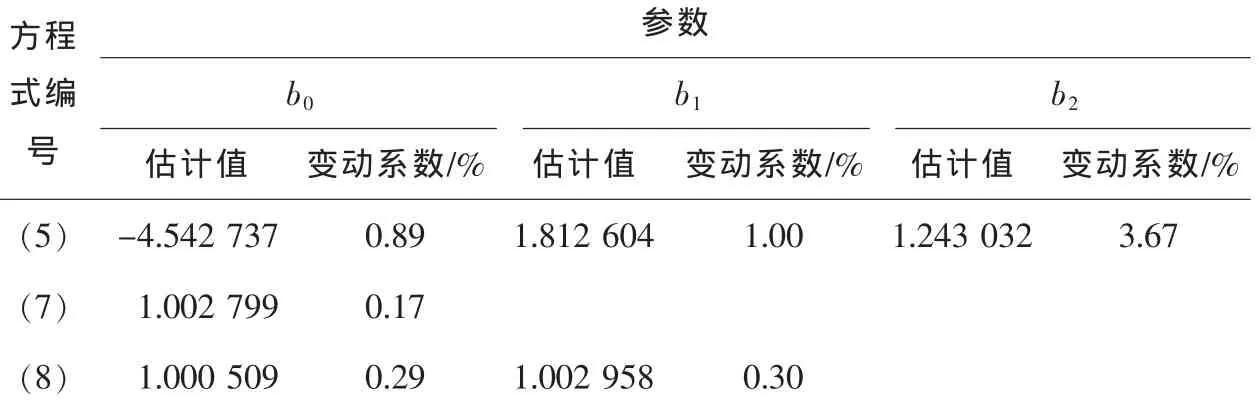
表5 去皮材积方程参数估计Table5 Parameter estimation of under-bark volume models

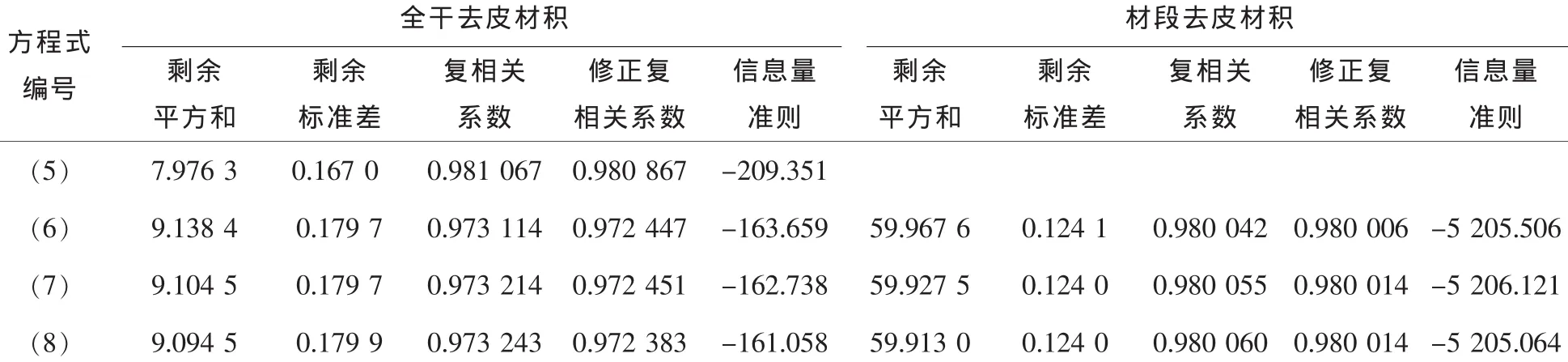
表6 全干及材段材积方程比较Table6 Comparation of volume models

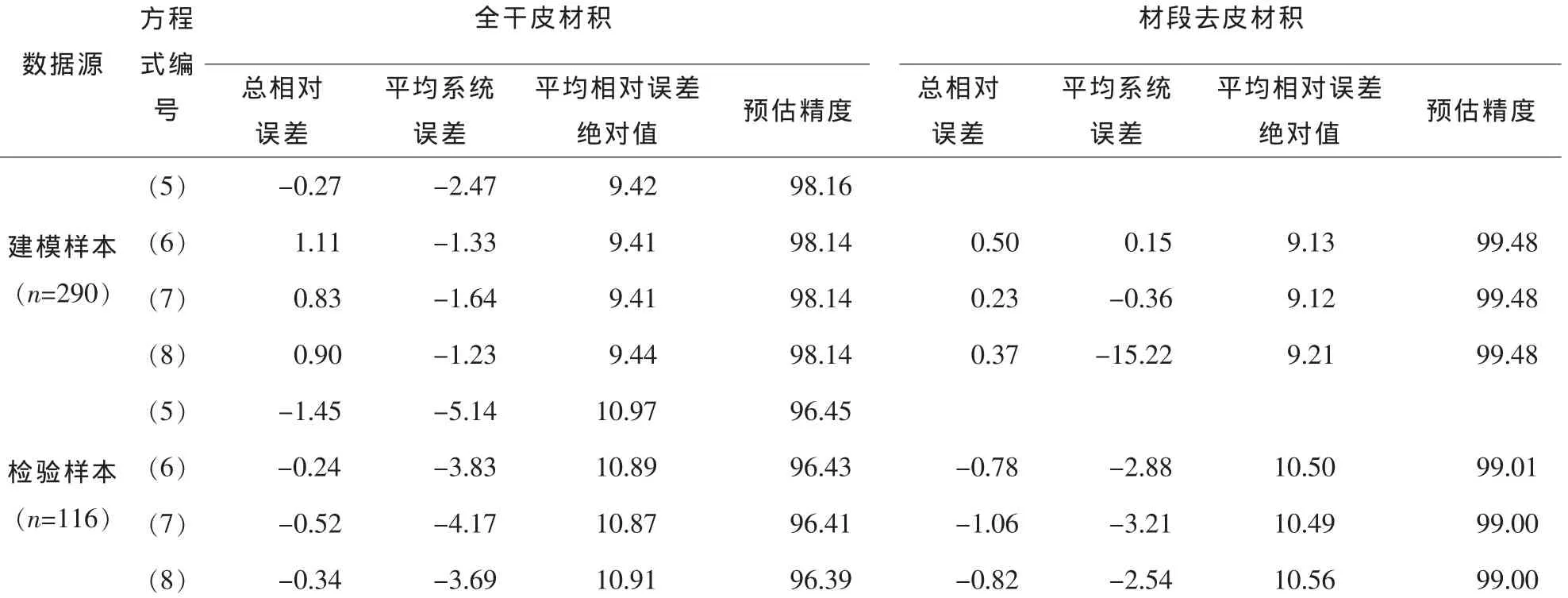
表7 全干、材段去皮材积方程模型评价指标Table7 Model test indexes for under-bark volume functions

2.5 树皮率方程

树皮率是指全干树皮材积占全干带皮材积的百分比。由于削度方程以及由其发展的累积材积方程均针对去皮材段，而材种出材率针对全干带皮材积，因此，需要估算带皮材积。由于树皮材积模型的预测效果不如去皮材积模型，故以修正削度方程积分材积加树皮材积作为全干带皮材积，树皮率及材种出材率以该带皮材积计算。

经试验，采用表现优秀的式（6）作为树皮材积方程。该方程形式上与山本材积式相同。

式（9）中：Vb为树皮材积，其他如前文。

树皮材积方程参数拟合结果（Box-Cox函数变换参数λ=-0.2）为：b0=-4.645120（变异系数=2.55%），b1=1.981140（变异系数 =2.81%），b2=0.478215（变异系数 =29.09%）；剩余标准差 =0.075468，修正复相关系数=0.754505，平均系统误差=-6.47%，预估精度为93.91%。

3 单株木二元材种出材率表的编制与精度检验

造材和编表程序在R软件平台上实现。按照先造大材，后造小材的原则进行造材。材种规格按照大、中、小径材小头直径分别不小于26.0，20.0，6.0 cm，其材长均不小于2.0 m，短小材小头直径不小于4.0 cm且不大于12.0 cm，其材长不小于1.0 m且不大于4.8 m的要求进行。理论造材采用的伐桩高度为10.0 cm。马尾松单株木二元材种出材率表样表见表8。全干带皮材积和树皮率分别采用式（10）和式（11）：

以上式（10）（11）中，V为全干带皮材积，V′（H）为全干去皮材积，Vb树皮材积，Pb（%）为树皮率。

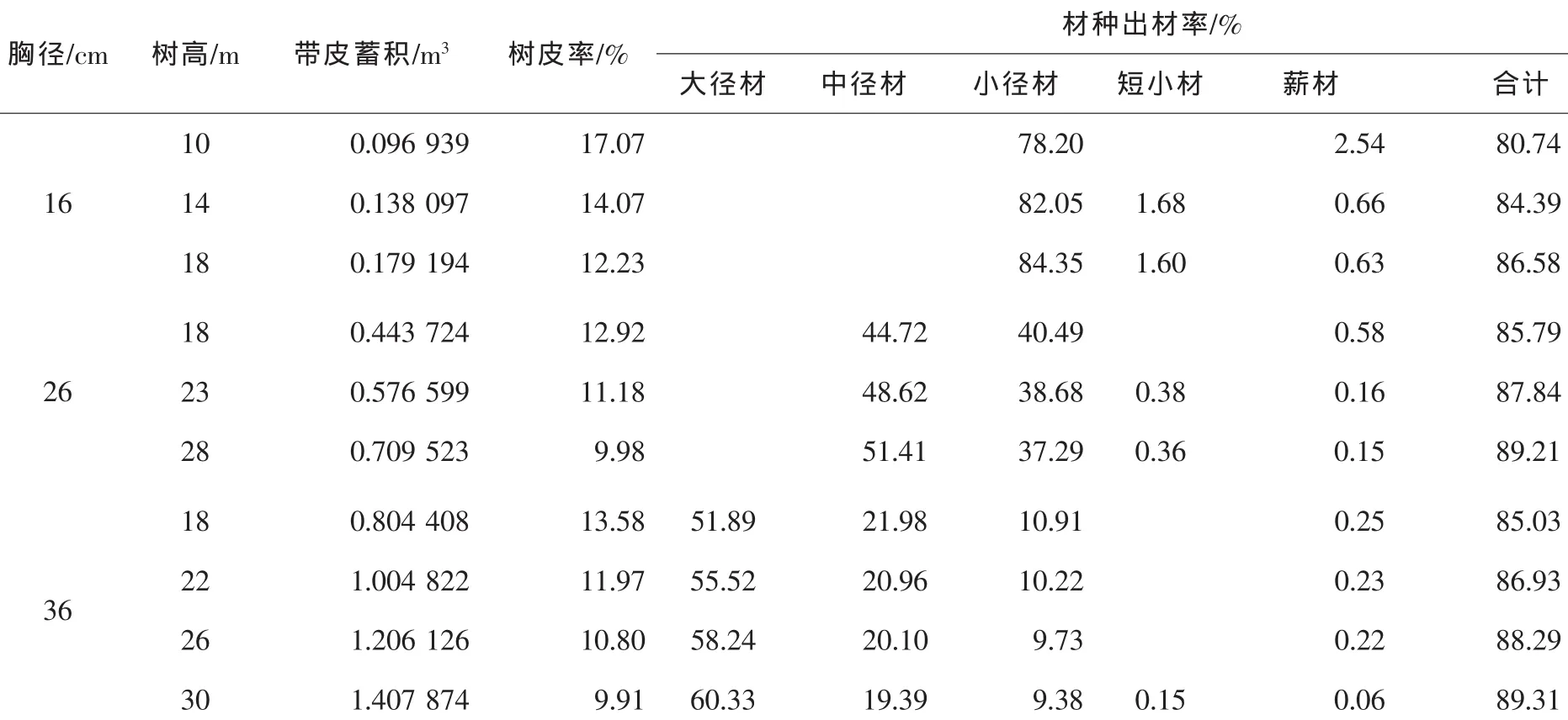
表8 马尾松单株木二元材种出材率表简表Table8 Two-dimention merchantable volume yielding volume rate tables of Pinus massoniana

编表精度的检验采用式（12），使用精度的检验采用置信椭圆F检验[9]。各材种的观测值采用模拟造材的方法获取。该方法以样木为单位，以各断面带去皮径为基础点，用Stine插值法获取带去皮树干的模拟曲线，再按照造材规格要求进行造材。精度检验的结果见表9。从表中可以看出，大、中、小径材3个材种均满足国家标准GB/T 20381-2006“材种出材率表编制技术规程”（下文简称 “国家标准”）不超过±5%的要求，经济材（包括大、中、小径材）平均系统误差为0.58%，满足国家标准不超过±3%的要求。短小材和薪材的平均系统误差较大，均超出±5%。置信椭圆F检验表明，除小径材和经济材未通过检验（0.01＜P＜0.05）外， 其他各材种均通过检验（P＜0.01）。

式（12）中：E为编表精度，yi为具体某一材种观察值，为该材种估计值。

4 小结与讨论

经参数优化的Kozak削度式（4*）， 累积材积式（7）和树皮材积式（9），共同组成了马尾松单株木材种出材率模型系统。该系统在R软件平台上形成计算机造材程序。对材种出材率表的精度检验表明，基于该模型系统编制的马尾松二元材种出材率表对主要材种（大、中、小径材和三者共同构成的经济材）满足国家标准要求，且大、中径材、短小材和薪材通过置信椭圆F检验，仅小径材和由大、中、小径材组成的经济材未通过此检验。因此，可以得出以下2点结论：①该马尾松单株木材种出材率模型系统具有一定的可靠性和预估精度；②该马尾松二元材种出材率表满足国家标准技术要求，具有应用和推广价值。

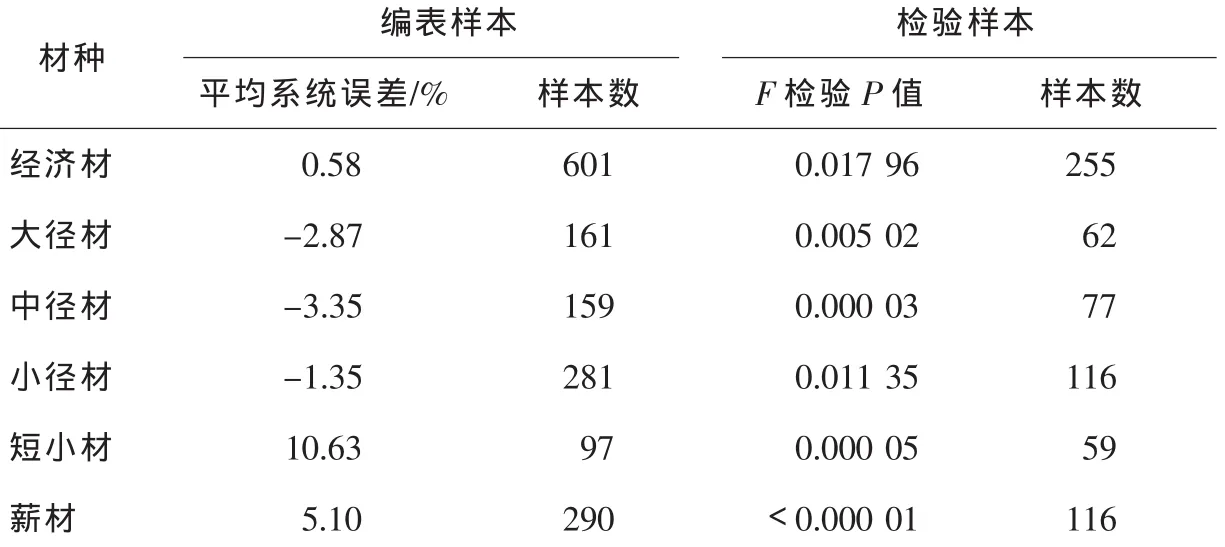
表9 马尾松材种出材率表的精度检验Table9 Accuracy test for merchantable volume yielding rate tables of Pinus massoniana

就削度方程而言，经参数优化的Kozak削度方程式（4*）在所考察的3个方程中表现最优，它能很好地体现马尾松中部饱满、基部膨大的干形特点，且具有很高的预估精度（＞99%）。Mak-Burkhart方程表现居中，Demearschalk方程表现表现最差。

累积材积方程的优选表明，把非一致性Kozak削度方程引入该方程的做法是可行的。用此方法获得的累积材积方程，可描述从树干基部到树干任意断面处的材段去皮材积，且在树干基部和顶部两端点的取值均有意义。

在树皮材积模型方面，形如山本材积式的树皮材积模型在一定程度上提高了树皮材积的预估效果。该方法预估树皮材积，有别于直接预估树皮率的做法，具有一定的借鉴意义。

总之，Kozak削度方程对马尾松干形的描述表现优异，以此方程为基础构建的累积材积方程具有很好的数学特性和预估效果，两者再加上形如山本材积方程的树皮材积方程，共同组成具有一定预估精度和应用价值的马尾松单株木二元材种出材率模型系统。

[1]朱松，夏忠胜.贵州省第3次森林资源规划设计调查森林资源报告[R]//贵州省林业厅.贵州省第3次森林资源规划设计调查报告集.贵阳：贵州大学，2009：1-80.

[2]江希钿，杨锦昌，温素平.马尾松可变参数削度方程及应用[J].福建林学院学报，2000，20（4）：294-297.JIANG Xidian， YANG Jinchang， WEN Suping.Study and application of taper equation of variable parameter of Pinus massoniana [J].J Fujian Coll For， 2000， 20 （4）： 294-297.

[3]江希钿，林文龙，刘玉明，等.马尾松人工林材种出材率表的编制[J].林业勘察设计，2001（2）：10-13.JIANG Xidian， LIN Wenlong， LIU Yuming， et al.The development of merchantable volume yielding rate tables of masson pine from artifitial forest[J].For Invest Des， 2001 （2）： 10-13.

[4]林剑峰.马尾松人工林材种出材率表的研究[J].北京林业大学学报，2001，23（4）：35-38.LIN Jianfeng.Research on log rule of timbers from artificial masson pine forest [J].J Beijing For Univ， 2001， 23（4）： 35-38.

[5]王鹏程，庄尔奇，涂炳坤，等.湖北省马尾松人工林削度方程及材种出材率表的研究[J].华中农业大学学报，2001，20（1）： 67-72.WANG Pengcheng， ZHUANG Erqi， TU Bingkun， et al.A study on the taper function and merchantable volume yielding rate table of mason pine in Hubei Province [J].J Huazhong Agric Univ， 2001， 20 （1）： 67-72.

[6]R DEVELOPMENT CORE TEAM.R： A Language and Environment for Statistical Computing [CP/OL].[2010-12-16].http：//ftp.ctex.org/mirrors/CRAN/.

[7]RITZ C， STREIBIG J C.Nonlinear Regression with R [M].New York： Springer， 2008.

[8]曾伟生，骆期邦，贺东北.论加权回归与建模[J].林业科学，1999，35（5）：5-11.ZENG Weisheng， LUO Qibang， HE Dongbei.Research on weighting regression and modelling [J].Sci Silv Sin， 1999， 35（5）： 5-11.

[9]中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB/T 20381-2006材种出材率表编制技术规程[S].北京：中国标准出版社，2006.

[10]孟宪宇.削度方程和林分直径结构在编制材种表中的重要意义[J].北京林业大学学报，1991，13（2）：14-19.MENG Xianyu.The significance of taper equations and stand diameter structures in developing merchantable volume tables [J].J Beijing For Univ， 1991， 13 （2）： 14-19.

[11]TOMAS J， HALLDOR B， ICELANDIC M O， et al.Stinepack： Stineman， A Consistently Well Behaved Method of Interpolation[CP/OL].[2009-03-20].http： //ftp.ctex.org/mirrors/CRAN/.

[12]EERIKÄINEN K.Stem volume models with random coefficients for Pinus kesiya in Tanzania， Zambia， and Zimbabwe [J].Can J For Res， 2001， 31 （5）： 879-888.