基于FPGA和DSP Builder的FIR数字滤波器设计
2011-05-29马桂芳刘生建
马桂芳 刘生建
(龙岩学院物理与机电工程学院,福建 龙岩 364012)
随着信息与数字技术的发展,数字信号处理已成为当今极其重要的学科与技术领域之一。而数字信号处理领域中的重要环节之一就是数字滤波器。数字滤波器根据数字滤波器冲激响应的时域特性,可分为有限长冲激响应(FIR)滤波器和无限长冲激响应(IIR)滤波器。FIR滤波器具有只有零点、系统稳定、线性相位、设计更为灵活的特性,因此在实际中得到更为广泛的应用。
1 FIR滤波器的方案设计
FIR滤波器的方案设计采用基于DSP Builder的FPGA设计方法。利用Matlab的FDATool(Filter Design&Analysis Tool)工具计算所要设计的FIR数字滤波器的参数;然后根据要求,使用DSP Builder设计FIR数字滤波器,并下载到FPGA进行硬件测试。该方案使FIR数字滤波器设计简单易行,并能满足设计要求。图1为FIR滤波器的系统框图。

图1 FIR数字滤波器的系统框图
2 FIR滤波器的DSP Builder设计
2.1 设计原理
对于一个FIR滤波器系统,它的冲激响应总是有限长的,其数学表达式用差分方程可以表示为:
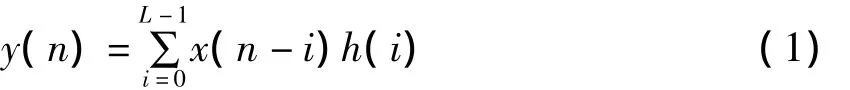
其中,x(n-i)是输入采样序列;h(i)是滤波器系数;L是FIR滤波器的阶数;y(n)表示滤波器的输出序列。
滤波器就是要寻求一个可实现的系统函数H(z),使其频率响应H(ejω)满足所希望得到的频域信号。结合FIR滤波器的实现指标,可知本设计的冲激响应h(n)应满足式(2),h(n)为偶对称,N为偶数:

H(ejω)的幅值关于ω=π成奇对称,不适合作高通。
在实际进行数字信号处理时,往往需要把信号的观察时间限制在一定的时间间隔内,只需要选择一段时间信号对其进行分析。这样,取用有限个数据,即将信号数据截断的过程就等于将信号进行加窗函数操作。选窗标准[1]如下:
①较低的旁瓣幅度,尤其是第一旁瓣。
②旁瓣幅度要下降得快,以利于增加阻带衰减。
③主瓣宽度要窄,这样滤波器过渡带较窄。
根据标准可知,要设计符合题目要求的FIR滤波器,需要选择哈明窗(海明窗)作为本设计的窗函数类型,具体参数如表1。

表1 哈明窗函数的基本参数
2.2 参数的确定
FDATool是Matlab信号处理工具箱里专用的滤波器设计分析工具,Matlab 6.0以上的版本还专门增加了滤波器设计工具箱。FDATool可以设计几乎所有的基本的常规滤波器,包括FIR和IIR的各种设计方法。它操作简单,方便灵活。
启动 Matlab的 FDATool工具,选择 Dsign Filter,指定FIR数字滤波器为低通滤波器,采样频率fs为20 MHz,截止频率 fc为500 kHz,使用窗函数(hamming),将滤波器阶数设置为31。这是由于设置了32阶FIR滤波器的常数系数项h(0)=0。此时可利用FDATool有关工具分析所设计出的滤波器的幅频特性、相频特性、冲激响应、阶跃响应、零极点等。由于导出的滤波器系数是一个一维的小数变量NUM,而VHDL综合器又不支持实数,因此要在FIR滤波器模型中使用这些数据,需要在Matlab命令窗口输入:round(NUM*(2^8))。此时可以得到一系列的滤波器参数,具体如下:
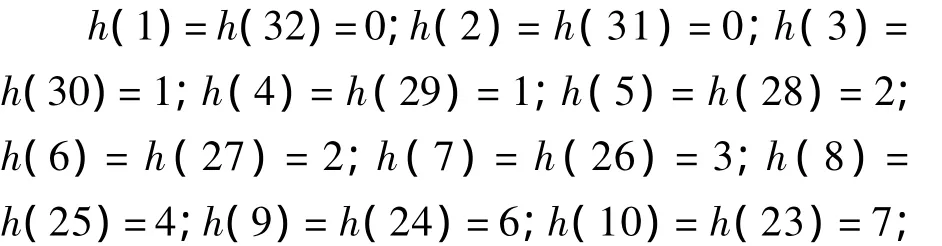
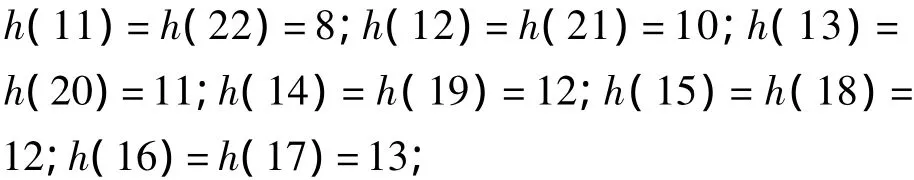
2.3 FIR滤波器的MDL
对于直接I型的FIR滤波器是可以级联的。在实际应用中通过不断地调用FIR滤波器节,级联起来,用来完成多阶FIR滤波器的设计。
基于这种思想方法,本系统先设计了一个8阶的FIR滤波器子系统,然后通过级联的方式,构成32阶FIR低通滤波器。
2.3.1 8阶低通FIR数字滤波器的MDL模型
根据FIR数字滤波器的结构原理设计一个低通的8阶FIR数字滤波器的MDL模型,如图2所示。接着把设计好的MDL模型文件创建成一个8阶FIR滤波器子系统并mask subsystem。
2.3.2 32阶低通FIR数字滤波器的MDL模型
复制4个8阶FIR滤波器子系统,并将子系统衔接起来,将确定的滤波器系数添加作为32个常数端口,把4个8阶滤波器子系统的输出端连接起来,接入一个加法器,从而得到32阶低通的FIR数字滤波器的输出。又因为其后面要接的是一个10位的DA芯片(THS5651),而该芯片的数据又是无符号类型的,所以需要对其输出截取高10位,并转化成无符号输出。这样才能在 Cyclone系列的FPGA平台上进行硬件测试。

图2 8阶低通FIR数字滤波器的MDL模型
3 FIR滤波器的FPGA
在建立顶层原理图前,要先生成32阶FIR数字滤波器的VQM文件,然后把生成的VQM文件复制到32阶FIR数字滤波器的文件夹里。
由DSP Builder生成的QuartusII工程,根据FPGA平台特性建立顶层原理图。在图3所示的FIR数字滤波器的顶层原理图中,设置输入时钟为20 MHz,然后通过PLL生成20 MHz时钟给片外的10位高速D/A部门电路和FIR数字滤波器使用,生成的20 MHz时钟经过二分频产生10 MHz时钟作为A/D转换器的时钟。
在FIR数字滤波器的顶层原理图建立后,应将其输入输出信号锁定在芯片确定的引脚上,编译后下载,以便能对所设计的FIR数字滤波器进行硬件测试。因此先设置FPGA芯片类型为Cyclone系列GWAC6 EP1C6Q240C8,然后通过查阅有关芯片引脚对照表进行引脚锁定,最后存储这些引脚锁定的信息。在以上步骤完成后还必须在编译(启动 Start Compilation)[2]1 次,才能将引脚锁定信息编译进编程下载文件中。此后就可以准备将编译好的SOF文件下载到实验系统的FPGA中去了。

图3 FIR数字滤波器的顶层原理图
4 FIR滤波器系统仿真
如图3所示,在32阶低通的FIR数字滤波器的MDL模型文件中添加20 MHz的正弦波和500 kHz的正弦波,并把叠加后得到的波形作为该滤波器的信号源,在输出端口和输入端口分别添加一个2通道示波器来观察波形和一个频谱分析仪来观察频谱的分布。其中20 MHz的正弦波和500 kHz的正弦波的类型是基于采样的。在仿真前,先进行该滤波器的 configuration parameters。设仿真时间为3000 s,type为fixed-step,solver为discrete(no continuous states),接着点击 simulation-start来启动32阶低通FIR数字滤波器的功能仿真,观察到的结果如图4所示。
由图4可以得出,所设计的32阶低通FIR滤波器不仅实现了滤除混叠波中的高频成分(20 MHz)的功能,而且具有线性相位的特点,符合设计要求。
5 FIR滤波器的性能研究
数字信号处理系统实际上是由运行在数字计算机上的软件实现的,在这种情况下,由于有限精度运算而造成的量化误差都是固有的,其误差类型有:
①将输入信号量化到一组离散电平上而引入的误差,如模数转换。
②用有限字长表示乘法系数而造成的滤波器频率响应误差或变换系数误差。
③在加法之前或之后对诸如乘法输出等内部数据进行量化而造成的误差。
本设计需要用到A/D变换器来完成将模拟信号转换为数字信号,即将输入的模拟信号转换为b位二进制数字信号。变换器位数有限,因而存在量化误差,其量化误差取决于量化位数,位数越多量化误差就越少。如N位的A/D转换器,其量化误差为1/2N+1。本设计采用的A/D转换器(TLC5540)输入数据为8位,其量化误差为1/512。
在本设计中采用逼近法来设计FIR数字滤波器时,是在无限精度的假设条件下计算滤波器的系数。在实际实现时,这些系数要被量化,要用有限的字长来表示,因而实际滤波器的时间和频率响应与理想情况会有偏差。经过量化后的FIR滤波器的幅频、相频性能会有所改变。
6 结语
本文主要采用基于FPGA和DSP Builder技术,设计了一个低通的32阶FIR数字滤波器,并分析了所设计的低通FIR数字滤波器的性能,从而实现了滤除混叠波的功能。该设计克服了传统的设计方法(如:FPGA、Matlab等)的缺点,提高了系统的分辨率,只有切换速度快,具有切换相位连续、输出信号相位噪声低、可编程、全数字化易于集成、体积小、重量轻等优点。系统设计考虑的诸多要素中,保持系统的稳定性与抗干扰性是开发的关键,因此应该慎重选择适合的方案。

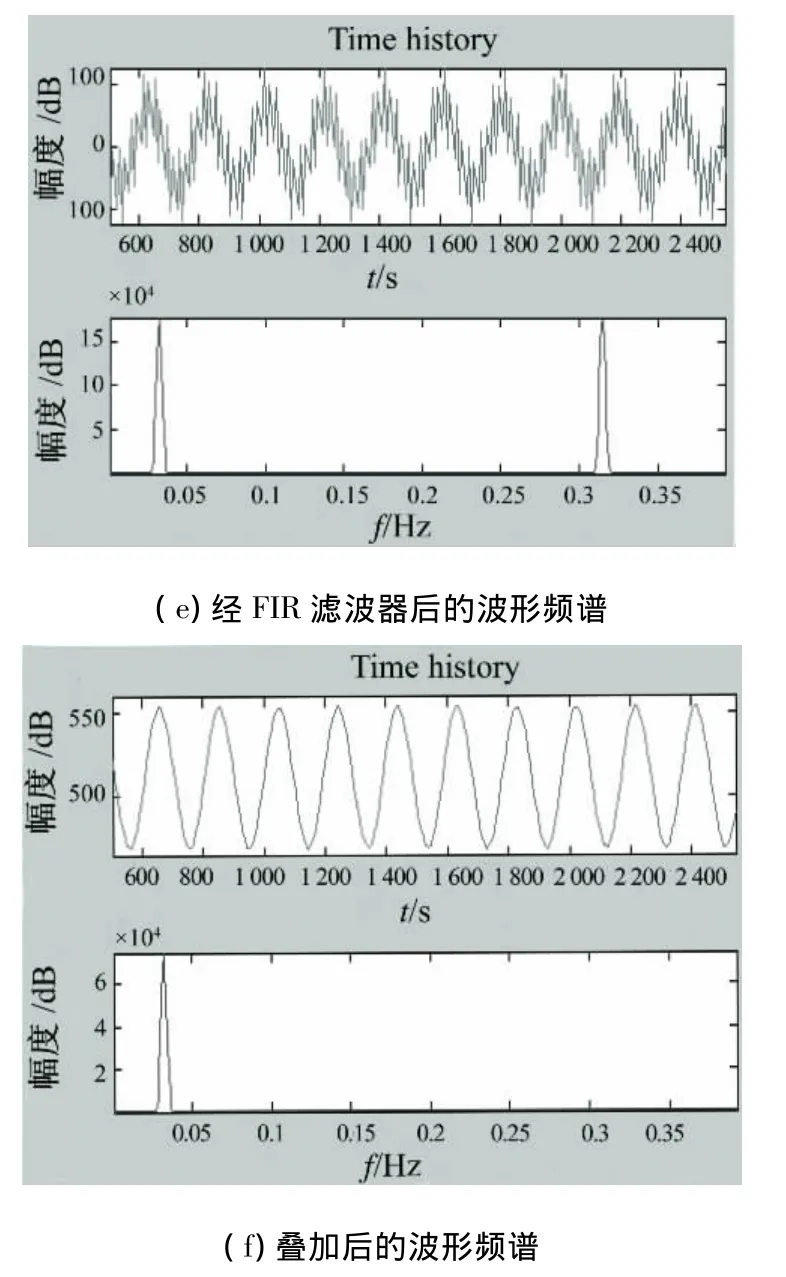
图4 时间关系曲线
[1]黄亮,张友纯.基于FPGA的FIR滤波器的设计与实现[J].现代电子技术,2006(10):20-22.
[2]潘松,黄继业,王国栋.现代DSP技术[M].西安:西安电子科技大学出版社,2004.
[3]潘松,黄继业.EDA技术使用教程[M].西安:西安电子科技大学出版社,2004.
[4]胡广书.数字信号处理——理论、算法与实现[M].北京:清华大学出版社,2002.
[5]杨丽杰,崔葛瑾.基于 FPGA的 FIR滤波器设计方法的研究[J].东北大学学报,2006,32(6):93 -96.
[6]齐海兵,曹志亮,刘春锦.基于DSP Builder的FIR滤波器的设计与实现[J].国外电子元器件,2006(7):7-9.
[7]张登奇,李望移.基于MATLAB的FIR滤波器的设计[J].计算机时代,20067(11):47 -49.
