数控螺杆铣床床身结构的动态优化设计
2011-05-28王海军孙兴伟
刘 杰,王海军,王 可,孙兴伟
(沈阳工业大学机械工程学院,沈阳 110870)
0 引言
机床作为复杂的机械系统常受振动与噪声等问题的干扰,严重影响机床的稳定切削及加工精度甚至减少机床的使用寿命,因此改善机床的动态特性成为机床优化设计的重要任务[1]。
影响机床动态性能的因素比较多也比较复杂,优化设计时必须做一些简化处理。机械结构的模块化设计无疑成为简化处理的重要手段,它是以有限元分析为核心建立既反应实际情况又便于计算的模型,通过结构的分析与优化使零件的动态性能得到提高,降低生产成本[2]。
1 优化设计的理论分析基础

一个n自由度的无阻尼振动系统可表示为:式中:[M]、[K]——质量和刚度矩阵;
{f}——外激励矩阵,这里为零矩阵;
{x}、{¨x}——物理坐标系下的位移和加速度矩阵。
式(1)的特征方程为:

解此方程得ω的m个互异正根,ω0i(i=1,2,…,m)并按升序排序,0<ω01<ω02<… <ω0m,第 i阶固有圆频率:
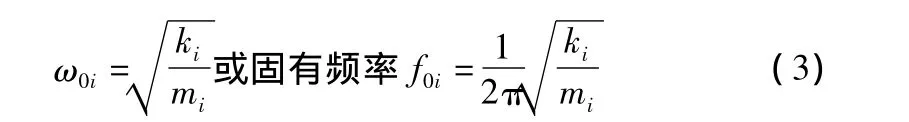
机床的动态优化的目标准则为[4]:①提高各阶固有频率;②保证具有一定抵抗受迫振动和自激振动的能力;③机床的固有频率应避开外界激振频率以免发生共振现象。
2 基于有限元的数控螺杆铣床床身动态特性分析
有限元分析的基本思想是:把一个被分析对象的连续体划分为有限个相互连接在n个结点上的单元,承受等效节点载荷,根据平衡条件进行分析[5]。再根据变形协调条件把这些单元重新组合为原形态体进行求解。
2.1 螺杆铣床床身有限元模型建立
建立有限元分析的基础是建立有限元分析模型,利用三维软件对原始床身结构建立实体模型,将其导入有限元软件进行分析是一种高效便捷的方法。
数控螺杆铣床床身为大型铸件,上面有诸多的螺纹孔、油槽孔、连接孔、圆角、倒角等细节特征,这些特征对庞大床身的动态特性几乎没有影响,因此为降低计算量提高分析效率要将这些细节特征省略。机床床身总长为 10000mm,高度为 680mm,床身跨度为810mm,床身内部分布着筋板,各筋板开有分布均匀的方形清砂孔。床身壁厚为25mm,筋板厚度为20mm,建立的三维模型如图1所示。

图1 床身的三维模型
2.2 螺杆铣床床身动态特性分析
模态分析是动态分析最基本的内容,目的是在给定的条件下得到某构件的固有频率及变形量[6],对机床床身的动态分析是基于有限元软件的模态分析,由于低阶固有振型对动态特性起决定性作用,故取床身的前四阶模态进行分析[7]。
将床身的模型导入有限元软件进行网格划分,由床身实际受力情况对其施加约束,求解得到床身的固有频率及最大变形量,床身振型描述如表1所示,图2为床身的第一阶振型。

图2 床身第一阶振型
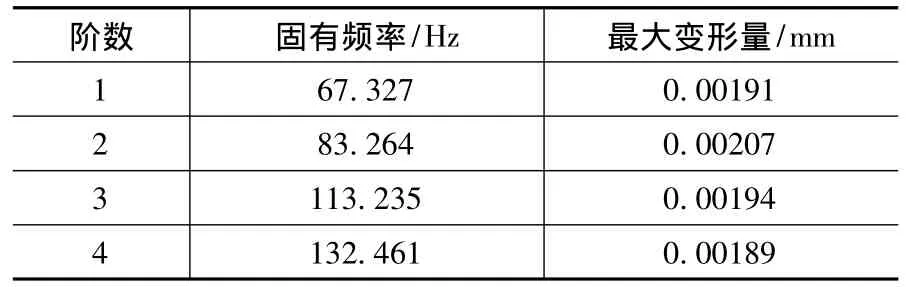
表1 原始床身前四阶固振型
2.3 成型盘铣刀的工作频率的计算
螺杆铣床可以看作是一个无阻尼振动系统,加工过程中外部激振力主要体现在切削力上。螺杆铣床刀具切削时的激振频率计算公式:

式中:n——转速;
Z——齿数。
机床切削时转速范围为0~150r/min,铣刀齿数为24,由上式算得激振频率范围为0~60HZ。由表1可知,床身的前四阶固有频率最小值为67.327Hz,与机床的最高激振频率60HZ接近,这在机床工作过程中,很容易产生共振,所以要适当改进机床床身结构,提高其固有频率值,使其远离共振频率范围。
3 床身结构优化
基于元结构的优化设计能有效的提高床身的刚度减小变形量。元结构是把机械结构大件就其组成的形体进行分解,最终可分解得一些拓扑结构变化不大、相对独立的基本单元结构,可称为元结构[9]。其结构单元特性会影响到整个结构特性的优劣。
床身包含内部纵横筋板结构(筋板开出砂孔)和导轨等主要元素。为了使元结构分析应用于复杂结构的设计中,要构造参数化元结构模型[10]。
现取床身结构的一节(即一个筋格长度)作为研究对象,分析此节床身底面开的出砂孔尺寸大小与固有频率的关系。如图3所示,方形出砂孔边长D,床身宽度l。

图3 底面纵向一个筋格结构示意图
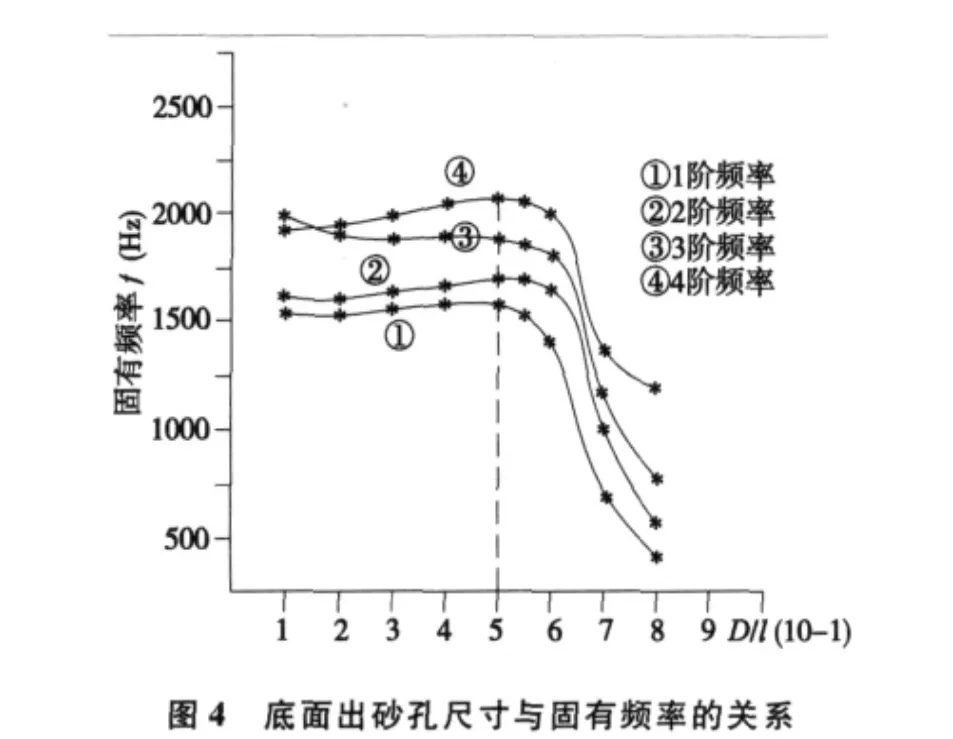
通过改变出砂孔尺寸D和床身有效宽度d的比值,能够分别得到相应的筋格元结构固有频率变化曲线(如图4)。
由曲线可知,当D/L=0.65时可以得到较高的固有频率和较大的出砂孔。
现分析床身横筋板出砂孔尺寸对床身固有频率的影响,出砂孔宽度为 D1,床身有效高度h(如图5所示)。
通过改变D1与h的比值得到床身固有频率的变化曲线(如图6)。
观察曲线可知,当D1/h=0.5时可获得较高的固有频率。


通过上述分析对床身作初步优化,分析可得到其前四阶振型,如表2所示。

表2 初步优化的床身前四阶振型
对比表1表2其固有频率已经得到一定的提高,但第一阶固有频率仍在频率禁区(即接近共振区)。为了进一步提高床身的固有频率,需进行结构再优化。原床身有纵向长支承筋板和数十个横向筋板,为提高固有频率在床身两侧支承中间再加一条厚度为20mm的纵向筋板,结构如图7所示。
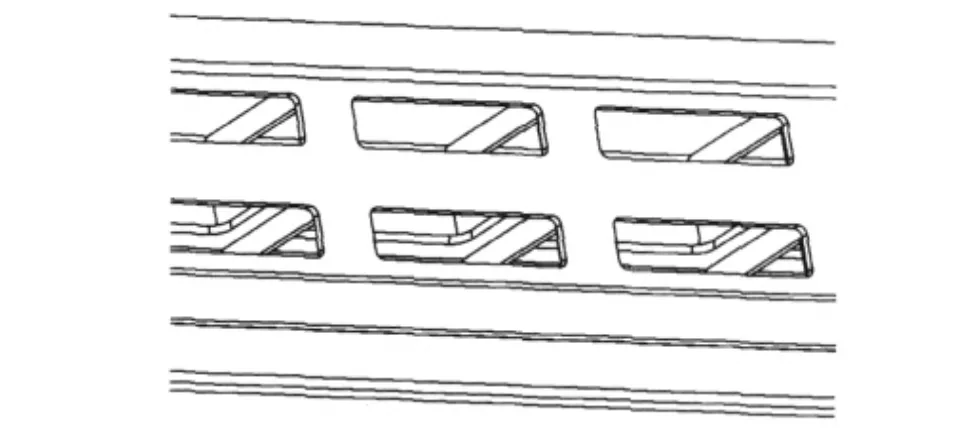
图7 优化后的床身结构
对上述优化的床身作动态分析,其前四阶振型如表3所示。

表3 优化后床身前四阶振型
与表1对比优化后床身的第一阶固有频率已提高45%,第二阶提高18%,第三阶提高9%,第四阶提高18%。优化后床身质量为5.0561t,比原来4.8559t增加约0.2t,床身质量虽有所增加但增加幅度很小,且能获得良好的动态特性,有效的避开了机床的频率禁区。
4 结束语
通过对床身的动态特性分析发现其设计不足,基于元结构的思想对床身结构作了优化设计,优化后床身的固有频率显著提高,最大提高45%。有效避开了机床系统的共振区域而且提高了机床整体刚度,获得满意的设计方案。
[1]何献忠,等.优化技术与应用[M].北京:北京工业学院出版社,1986.
[2]张海伟.数控机床动态性能的分析及其结构优化[J].制造技术与机床,2006(5):21-22.
[3]诸乃雄.机床动态设计原理与应用[M].上海:同济大学出版社,1987.
[4]李洪.实用机床设计手册[M].沈阳:辽宁科学技术出版社,1999.
[5]赵汝嘉.机械结构分析的有限元法[M].武汉:华中理工大学出版社,1998.
[6]刘国庆,杨庆东.ANSYS工程应用教程——机械篇[M].北京:中国铁道出版社,2003.
[7]康芳,范晋伟.基于ANSYS的数控机床动态特性分析[J].机械设计与制造,2008(7):181-182.
[8]韩博.方钻杆数控机床切削稳定性研究[D].沈阳:沈阳工业大学机械系,2010.
[9]张学玲,徐燕申,钟伟泓.基于有限元的数控机床床身结构动态优化设计方法研究[J].机械强度,2005,27(3):353-357.
