丙烯酸酯单体组成与粘度的关系

王德海,胡祥太,蒋 辉,陈 敏

(浙江工业大学化学工程与材料学院,浙江 杭州 310032)

粘度是作为一种流体的液体涂料的主要物理特性之一,粘度值反应了液体分子间由于相互作用而产生的流动阻力[1].液体涂料的流变性对于其贮存稳定性、施工性能和成膜性能都有很大的影响[2].纯液体的粘度基本上都有文献记载,有关纯物质在不同温度下的粘度的估算也有大量文献介绍[3].作为复杂丙烯酸酯类单体,其组成千变万化,逐一测定他们的粘度是不可能的.所以,由单纯液体的粘度预测混合液体的粘度,进一步将其应用于UV涂料单体粘度的预测,成为粘度研究领域的发展趋势.目前粘度预测模型有Przezdziecki-Sridhar模型[4]、Sastri-Rao模型[4]、PRη模型[5]以及 Dymond-Assael硬球模型[6]等.这些模型方程需要较多参数,而且形式比较复杂.从质量分数和摩尔分数角度进行预测的传统方程,虽然参数较少,形式简单,但实验发现预测误差较大,然而,正是由于这一不足,为传统方程的改进提供了可能.笔者在传统方程的基础上,引入一些参数进行修正,得到了一些新方程,并与传统方程在预测精度上进行了比较.

1 实验部分

1.1 实验原料

1,6-己二醇二丙烯酸酯HDDA,EM221,长兴公司;二缩三丙二醇二丙烯酸酯TPGDA,EM223,长兴公司;三羟甲基丙烷三丙烯酸酯TMPTA,EM231,长兴公司;乙氧化三羟甲基丙烷三丙烯酸酯 TMP3EOTA,SR454NS,沙多玛公司;乙氧化三羟甲基丙烷三丙烯酸酯TMP9EOTA,SR502,沙多玛公司.

1.2 实验仪器

J890-D强力电动搅拌机,上海标本模型厂;NDJ-4旋转粘度计,同济大学机电厂.

1.3 实验方法

按一定的配方称料(需搅拌的用强力电动搅拌机搅拌30 min),选择适宜倍率的转子,调节所需温度,用旋转粘度计测量不同温度下试样的粘度.

2 结果与讨论

2.1 对传统的粘度预测方程的修正

据文献[7]介绍,理想的(即不相互作用的)混合溶剂的粘度可由下式精确地求得,即

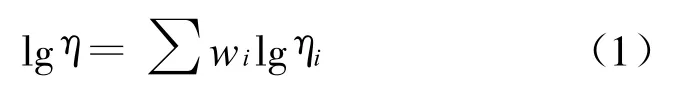
据文献[8]介绍,对于混合液体,其粘度η可根据各组分纯态粘度值及混合物组成,通过下述经验公式计算,即

式(1,2)中:η表示混合物的粘度,mPa·s;wi表示第i组分的质量分数,%;ni表示第i组分的摩尔分数,%;ηi表示第i组分的自身粘度,mPa·s.

比较上述两传统方程发现,它们的形式是一样的,而式(2)中的ni可以看作是用结构参数分子量M修正wi的结果.

然而,混合液体的粘度应该是各组分不同形态分子之间相互作用的结果,仅仅用分子量描述是不够的.鉴于此,考虑引入其他一些结构参数进一步修正.

表征分子结构的参数很多,常见的有溶度参数δ、范德华体积V及活化能E等.溶度参数可表征分子间的相互作用,衡量物质间的相容性[9-10];范德华体积可认为是该分子所占据的空间,表征分子的大小[11];而活化能则在一定程度上反映了分子链的柔顺程度[12].将这些参数引入修正ni,结果如表1所示.实验中各物质的基本结构参数如表2所示.

表1 引入参数修正ni的结果Table 1 The results from amending niby drawing into some parameters

表2 结构参数一览表1)Table 2 The structure parameters of monomers

2.2 线性回归

实验用NDJ-4旋转粘度计测定了不同温度下HDDA,TPGDA,TMPTA两两混合与三混合的粘度,将 lgη分别对wi,ni,si,fi,ei,pi,qi进行了线性回归,比较了它们的复线性相关系数,结果列于表3.

表3 HDDA,TPGDA,TMPTA两两混合与三混合的线性相关系数Table 3 The linear correlation coefficient when blending of two or three in HDDA,TPGDA,TMPTA

从表3可以看出,用修正方程回归所得的线性相关系数有所提高,整体来看,其中尤以 lgη=∑pilgηi,lgη=∑qilgηi方程回归所得的线性相关系数最接近1.

2.3 预测方程计算值与实验值的比较

将lgη= ∑wilgηi,lgη= ∑nilgηi,lgη= ∑pilgηi,lgη=∑qilgηi方程的计算值与实验值进行了比较,结果如图1,2所示,并计算了相对误差,结果列于表4,5.

图1 300.15 K下不同配方混合物粘度预测方程计算值与实验值的比较Fig.1 The compare between calculated values and experimental values of different mixture at 300.15 K

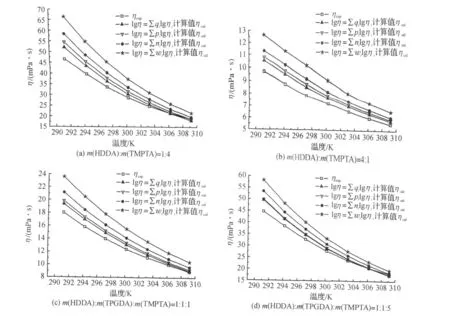
图2 不同温度下混合物粘度预测方程计算值与实验值的比较Fig.2 The compare between calculated values and experimental values of different mixture at different temperature

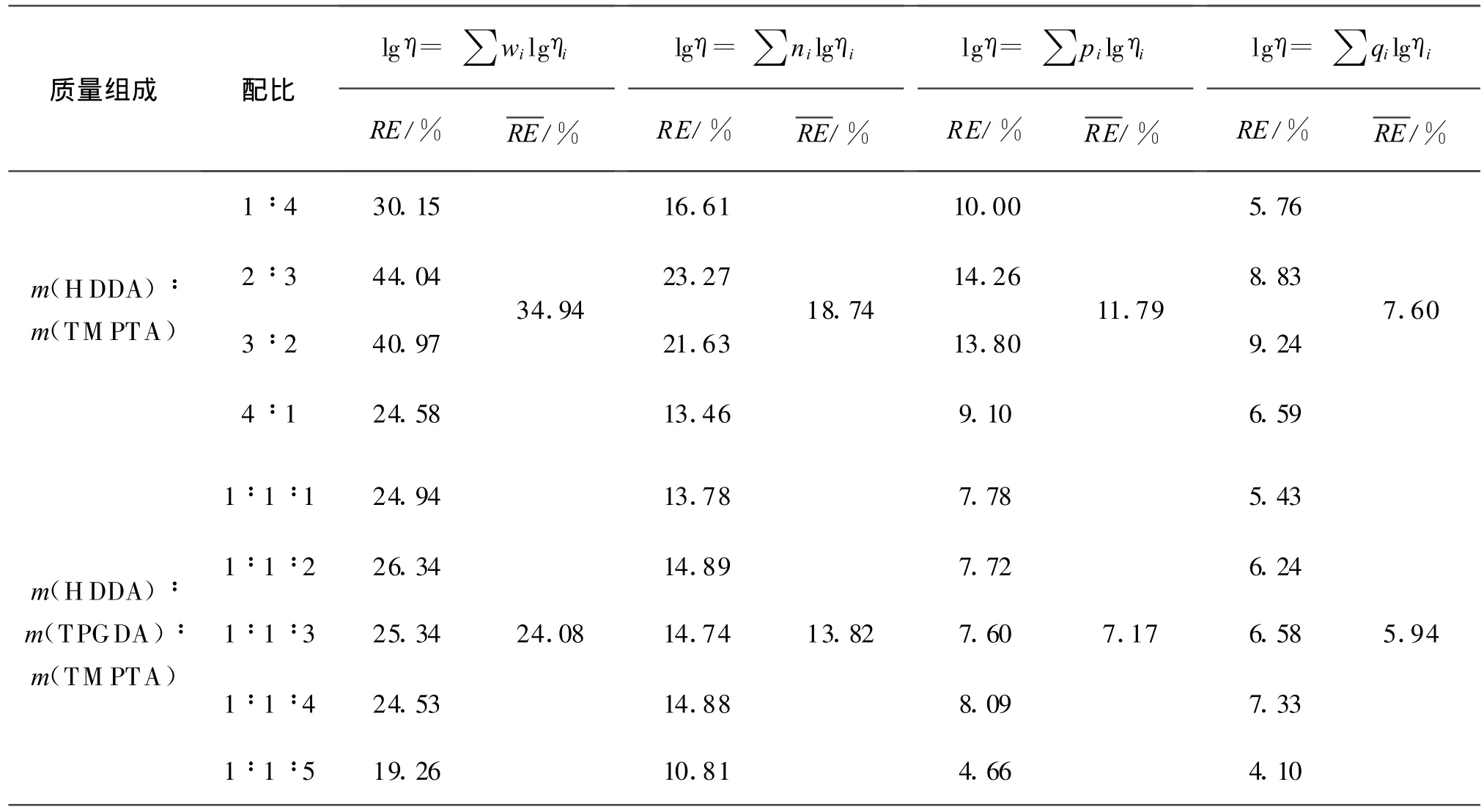
表4 300.15 K下不同配方混合物粘度预测方程计算值与实验值的相对误差比较1)Table 4 The compare of the relative error between calculated values and experimental values of different mixture at 300.15 K

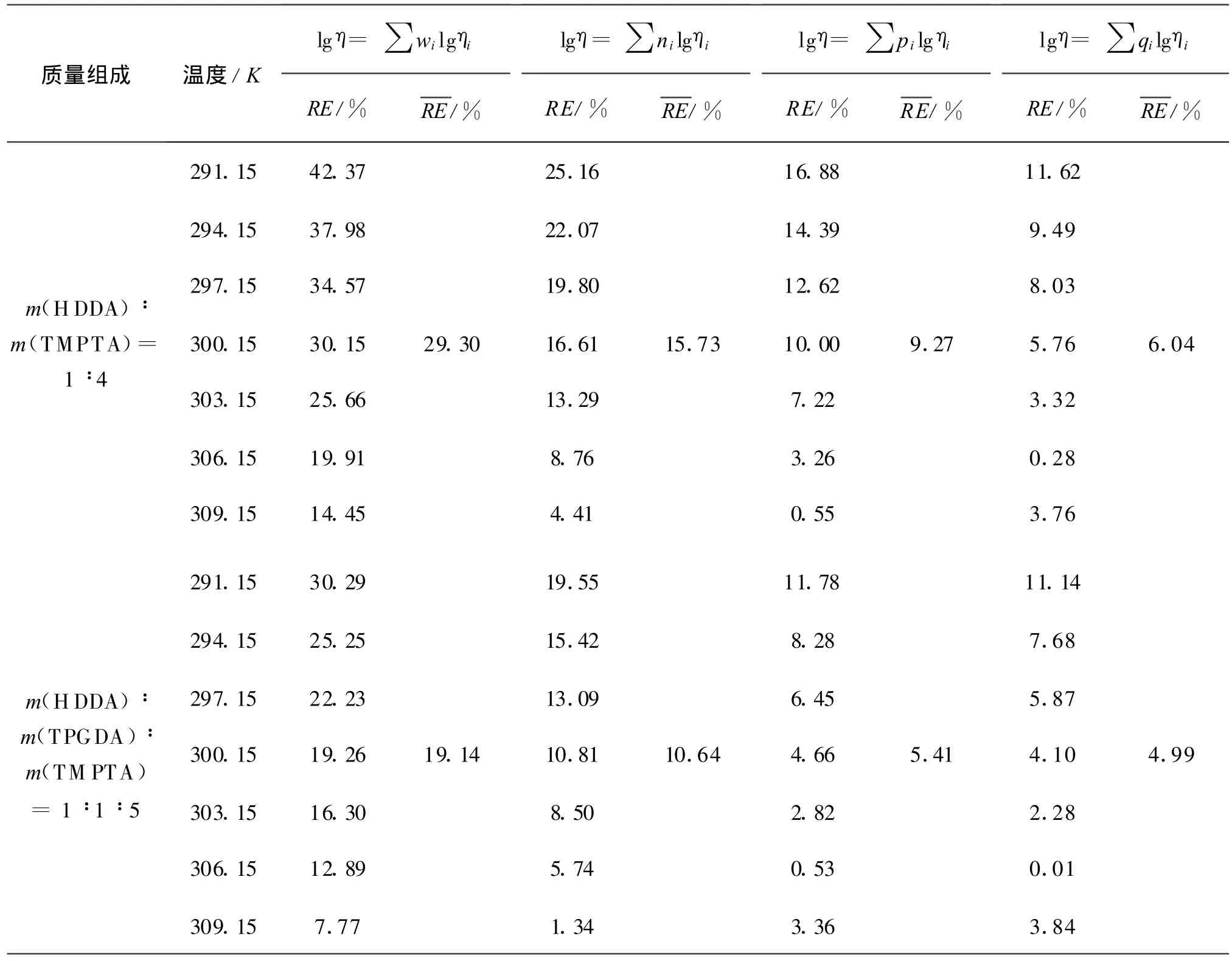
表5 不同温度下混合物粘度预测方程计算值与实验值的相对误差比较1)Table 5 The compare of the relative error between calculated values and experimental values of different mixture at different temperature

从图1,2可以看出,组成变化或是温度变化时,修正方程lgη=∑pilgηi,lgη=∑qilgηi的计算值比传统方程lgη=∑wilgηi,lgη=∑nilgηi的计算值都更接近实验值.在较高温度下,修正方程体现出了更好的适应性.这是因为,温度越高,分子运动越剧烈,不同结构形态的分子对粘度的不同贡献就越明显,所以修正方程在较高温度下体现出了更好的适应性.

从表4,5的相对误差比较中可以看出,修正方程lgη=∑qilgηi计算的粘度值与实验值最接近,平均相对误差仅为4.99% ～7.60%,lgη=∑pilgηi计算结果的平均相对误差为5.41% ～11.79%,相比之下,传统方程lgη=∑nilgηi,lgη=∑wilgηi计算结果的误差较大,分别为10.64% ～18.74%,19.14%～34.94%.

综上所述,相对于传统方程而言,修正方程lgη=∑qilgηi对于小分子混合物的粘度预测体现出了较好的适应性.这是因为,分子结构形态的不同,对粘度的贡献也就不同,修正方程正是考虑这一特征后在传统方程的基础上进行修正的结果.

2.4 lgη=∑qilgηi方程对长链大分子混合物的应用

为了将lgη=∑qilgηi应用于长链大分子混合物的粘度预测上,我们设计了以下实验.将TMPTA,TMP3EOTA和TMP9EOTA混合(图3),用修正方程lgη=∑qilgηi预测了混合物的粘度,并与传统方程的预测值进行了比较,结果如图4所示,同时计算了相对误差,结果列于表6.

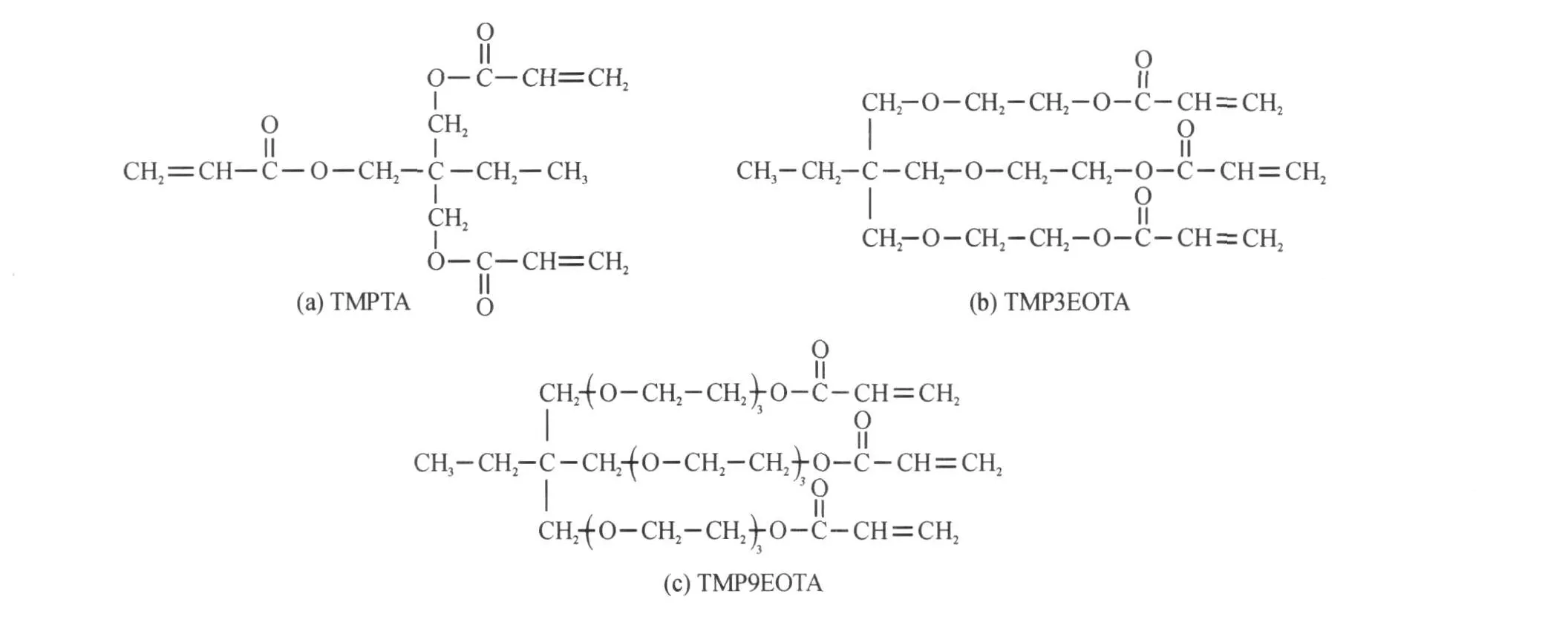
图3 分子结构图Fig.3 The molecular structure of matters

表6 298.15 K下TMPTA,TMP3EOTA和TMP9EOTA的混合物粘度预测相对误差的比较1)Table 6 The compare of the relative error between calculated values and experimental values of the mixture of TMPTA,TMP3EOTA and TMP9EOTA at 298.15.15 K

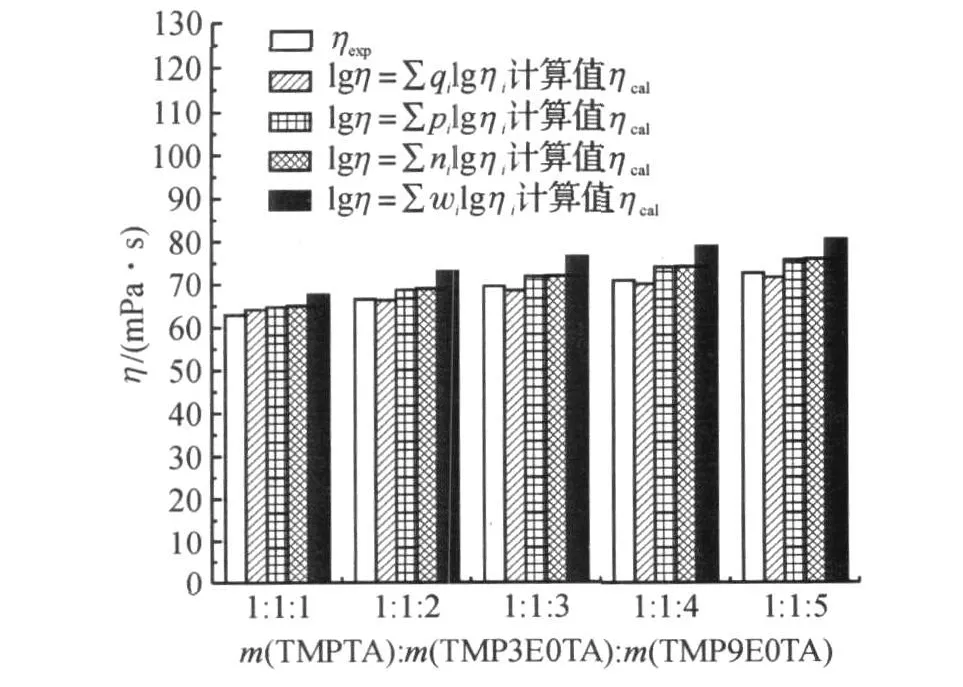
图4 298.15K下TMPTA,TMP3EOTA和TMP9EOTA混合时预测方程计算值与实验值的比较Fig.4 The compare between calculated values and experimental values of mixture blended with TMPTA,TMP3EOTA and TMP9EOTA at 298.15 K

从图4和表6可以看出,修正方程lgη=∑qilgηi对于长链大分子混合物的粘度预测仍然体现出了较好的适应性,平均相对误差仅为1.12%,而传统方程lgη=∑nilgηi,lgη=∑wilgηi平均相对误差分别为3.84%,9.66%.这是因为,分子结构形态越复杂,对粘度的不同贡献这一特征也就越明显,引入结构参数的修正方程也就能体现较好的适应性.

3 结 论

(1)线性回归分析结果表明溶度参数、范德华体积和活化能等结构参数的引入提高了方程的线性相关性,而其中尤 lgη= ∑pilgηi,lgη= ∑qilgηi方程的线性相关系数最接近1.

(2)修正方程lgη= ∑pilgηi,lgη= ∑qilgηi对小分子混合物粘度的计算值与实验值都很接近,平均相对误差分别为5.41%～11.79%,4.99%～7.60%.另外,修正方程在较高温度下体现出了更好的适应性.

(3)修正方程lgη=∑qilgηi对于长链大分子混合物的粘度预测仍然体现出了较好的适应性,平均相对误差仅为1.12%.

[1] 张小娟,陈秀芳.浅谈涂料黏度测定原理和检测方法[J].涂料技术与文摘,2004,25(4):29-31.

[2] 张军,戎宗明,李真德.高分子溶液粘度的测定、关联和预测[J].华东理工大学学报,2003(6):599-603.

[3] 衣守志,李海华,吴家全.对应态基团贡献法(CSGC)估算有机物液体黏度[J].天津科技大学学报,2008,23(1):1-5.

[4] POLING B E,P RAUSNITZ J M,O'CONNELL J P.The properties of gases and liquids[M].5th edition.Berkshire:M cGraw-Hill Education,2001.

[5] FAN Tian-bo,WANG Li-sheng.A viscosity model based on Peng-Robinson equation of state for light hydrocarbon liquids and gases[J].Fluid Phase Equilibria,2006,247:59-69.

[6] DYMOND J H,ASSAEL M J.In transport properties of fluids:their correlation prediction and estimation[M].New York:Cambridge University Press,1996:226-249.

[7] 涂料工艺编委会.涂料工艺[M].北京:化学工业出版社,1997.

[8] 刘引锋.涂料界面原理与应用[M].北京:化学工业出版社,2007.

[9] 高保娇.溶度参数及其应用[J].山西化工,1998(2):18-19.

[10] 孙志娟,张心亚,黄洪,等.溶解度参数的发展及应用[J].橡胶工业,2007,54(1):54-58.

[11] 安智珠.聚合物分子设计原理[M].长沙:湖南科学技术出版社,1985:43-51.

[12] 何曼君,陈维孝,董西侠.高分子物理[M].上海:复旦大学出版社,2005:114-119.