可靠性管理在电力生产中的应用
2011-05-24房中海谷新房何国亮
丁 杨,房中海,谷新房,何国亮
(沾化发电厂,山东 沾化 256800)
0 引言
可靠性工程始于二次世界大战,首先在军用电子工业中形成,20世纪60年代,美、日、英、前苏联等国将可靠性工程引入电力行业,逐步应用于电力系统的规划设计、电力系统调度、改进设备的可使用程度、安排检修计划、设备购买决策等。我国的电力可靠性管理中心成立于1985年,经过20多年的电力可靠性管理,使得我国电力工业的可靠性水平有了大幅度的提高。1986~2007年的22年间,我国100 MW容量等级以上火电机组的平均等效可用系数从79.93%提高到92.93%,增加了13%,每台机组年均非计划停运次数从7.85次/台·年下降到1.02次/台·年,平均下降6.83次/台·年。
1 可靠性在发电企业生产管理中的必要性
可靠性管理是运用科学的数理统计方法来定量的反映设备的健康水平、运行状况及设备制造、施工安装等方面的工作质量。通过对可靠性数据库资料的分析,找出设备故障分布规律,提前预测。做好预防措施,防止事故的发生,从而提高设备的可用率和生产能力。它着重研究设备或系统的故障原因、处理和预防措施,提高设备的可靠性,延长使用寿命、降低维护费用、提高设备的使用效益。
可靠性是衡量机组设备质量的重要技术经济指标。随着科学技术的不断发展和大型火电机组装机容量的增加以及自动化水平的提高,机组的可靠性问题已日益引起制造厂家和电力部门的重视。机组的特征是体积大、批量小、可修复、系统复杂、昼夜连续运行,设备损坏后将造成巨大的经济损失且后果严重。因此,必须高度重视机组设备质量,加强可靠性工程技术研究,其发展过程也可以看作是其设备故障逐步被解决、设备性能逐步完善、可靠性逐步提高的过程。特别是在机组的性能参数日益提高、设备结构日趋复杂的情况下,探讨和研究提高机组设备的可靠性将是一项非常重要的工作。目前,国内外机组设备招标中均有具体的可靠性指标的要求,可靠性已逐渐成为机组设备市场竞争的焦点和发电设备的重要依据之一。因此,探讨和研究机组设备的可靠性及提高可靠性的对策,就显得十分必要。
2 可靠性数据统计分析的常用模型
数据的统计分析是发电企业可靠性管理中研究的核心内容。由于设备的失效是随机的,其寿命不是定值而是随机变量,通过可靠性寿命试验及使用情况,获得产品的失效数据,用统计推断的方法来判断其属于哪一种分布。可靠性管理工作过程中,常用的分布有二项分布、指数分布、正态分布、泊松分布、对数正态分布和威布尔分布等,下面主要介绍二项分布、指数分布和正态分布。
2.1 可靠性分析的二项分布
二项分布满足以下基本假定:
1)试验次数n是一定的;
2)每次试验的结果只有两种,成功或失败,成功的概率为p,失败的概率为q,p+q=1;
3)每次试验的成功概率和失败概率相同,即p和q是常数;
4)所有试验是独立的。
在n次试验中,r次的成功的概率Pr为
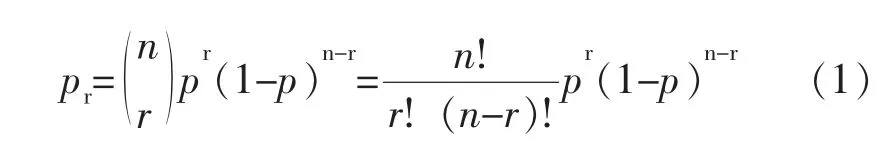
有时写为
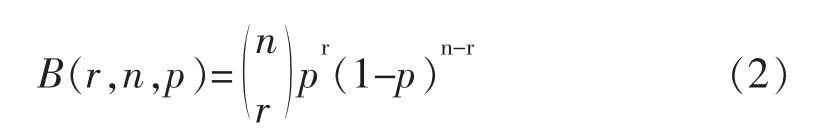
若随机变量X服从二项分布,那么期望值E(X)及方差Var(x)分别为:

式中:σ为标准差。

若有一个系统,含有n个相同的元件,至少有r个元件完好成为系统完好,那么系统完好的概率为
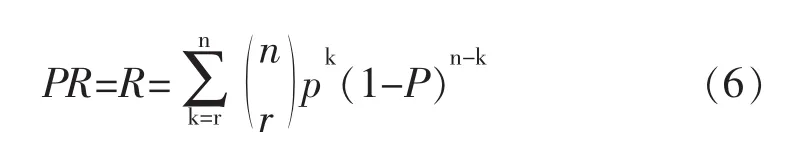
式中:p为一个元件完好的概率。称r<n的系统为冗余的系统。
如果一个系统有三个元件,每个元件有好和坏两种状态,若pi表示元件i完好的概率,qi表示元件失效的概率,那么可得到:
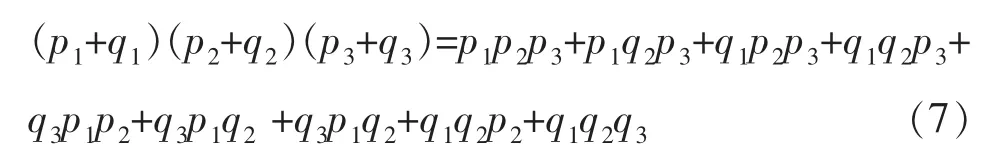
若元件是相同的,可以用二项式表示不同状态:
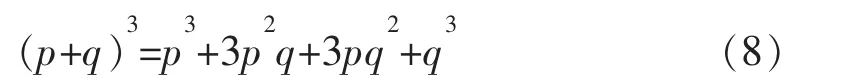
二项分布是一种离散性分布,广泛应用于可靠性和质量控制领域。在可靠性试验和可靠性设计中,常用于相同单元平行工作的冗余系统的可靠性指标的计算;另外二项分布在可靠性抽样检查中也很有用,在一定意义下,确定n个抽样样本所允许的不合格产品数,就需要用二项分布来计算。但在实际工程中,真正完全重复的现象是不多见的,应当根据实际的问题的性质来决定是否可以应用此模型来处理,例如“有放回”抽取是重复试验,而“无放回”抽取是不重复试验,但当产品的批量很大而抽取的样本量相对总数而言很小的时候,可以近似看作“有放回”抽样处理。
2.2 可靠性分析的指数分布
指数分布广泛应用于复杂系统的寿命分布,用T表示产品的寿命,t1,t2,…tn表示T的一组测量采集值,经统计可确定T的分布参数和分布类型,对于包含许多部件的系统可靠性指数分布表达式为
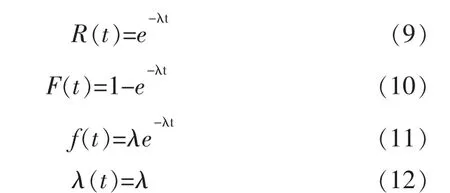
λ为故障率,表示单位时间里发生故障的次数。
在时段(0,T)中不发生及发生故障的概率分别为

接下来再研究在时段(T,T+t)的情况。
事件A表示在t时发生故障,事件B表示在时段(0,T)期间不发生故障。A∩B表示T以前完好,在(T,T+t)发生故障,即:


定义Fc(t)为T以前完好,在t时故障的概率,为后验概率:
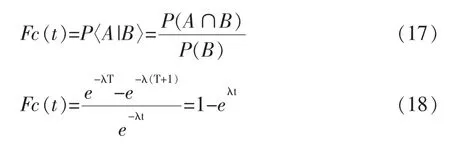
这表明,Fc(t)与运行过的时间T无关,它只与时间t有关,即无论元件运行多长时间,它们在下一段时间t发生故障的概率相同,同样可以理解为元件的质量不因使用时间的延长而下降。
元件的先验故障概率,即在(0,t)间故障的概率为:

对于指数分布,先验与后验概率是相等的

故障概率只与未来的时间有关,与历史无关,即它是无记忆性的。
对于指数分布,数学期望值和方差分别为

2.3 可靠性分析的正态分布
在发电企业锅炉设备中,锅炉部件的加工尺寸、材料强度、产品性能均服从正态分布模型。以寿命的均值E(t)=μ和标准差σ(D(t)=σ2)为参数的正态分布的计算公式可表示为:

3 可靠性管理在状态检修中应用实例
据有关资料统计分析,在火力发电企业中,机组非计划停运主要是由锅炉引起,其中锅炉四管泄漏为第一位,占强迫停运总时间的45%以上,对于超温过热所导致的爆管,通过内壁氧化皮厚度定量测量可以积极主动的预防,现就以锅炉爆管为例阐述一下可靠性管理在状态检修中应用。
超温过热导致内壁氧化皮的存在和管壁减薄是过热器爆管的必要条件,电站锅炉管内壁氧化层的增长厚度与其在该段服役期内的当量金属温度有一定的对应关系,通过监测管子内壁的氧化皮厚度和管壁厚度等相关参数计算出当量温度,研究表明当量温度可以作为超温爆管的特征信号,从该特征信号中选取分界值T0作为故障征兆。对于12Crl-MoV钢来说,T0=585℃。由于超温爆管的原因是壁厚减薄与蠕变,可以归结为应力—强度模型,该模型分布服从正态分布,故当量温度T服从正态分布。参数估计确定T的均值T和标准差σA后,过热器爆管概率F(T)为:
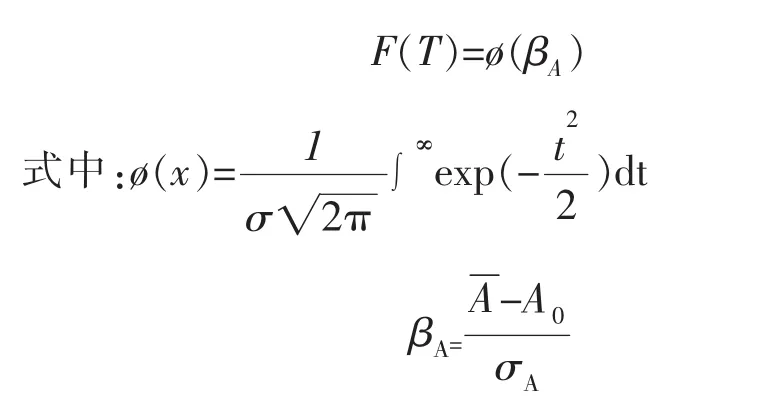
对某电站锅炉的高温过热器管进行寿命评估,其材质为12CrlMoV,已运行73 000 h,其中10根寿命小于3万h的管子依据内壁氧化皮厚度、金属层壁厚、管径周相应力估算的当量金属温度数据排序为594℃、589℃、593℃、592℃、596℃、597℃、587℃、597℃、596℃、595℃。

根据基于当量金属温度及运行应力的Larsonmiller公式、壁厚减壁薄率、氧化和腐蚀计算各管段的剩余寿命,以上的10根管子的剩余寿命从小到大为:15 235 h、15 924 h、16 581 h、17 084 h、18 774 h、19 429 h、21 238 h、27 871 h、28 529 h、28 935 h。 根据正态分布计算:
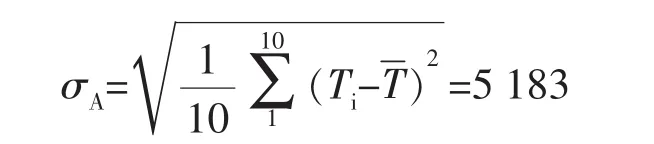
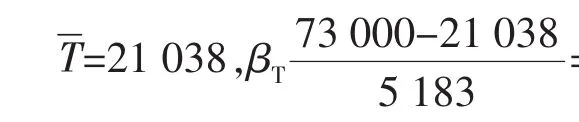
4 结论
目前已厂网分开,竞价上网逐步实施,对于发电企业来说每一次非计划停运损失不仅仅是在启停过程消耗的燃料费和少发电量,电网企业往往还会对每一次的非计划停运进行一定电量的考核,对发电企业来说提高其设备的可靠性同提高其运行的经济性同为重要。可靠性管理工作贯穿电力生产管理全过程,其不再局限于可靠性专责的单线管理,各有关生产单位的领导和工作人员通过对该系统的应用,使可靠性管理工作与日常各专业管理密切结合,把可靠性管理同状态检修有机结合,达到共同参与可靠性管理,并贯穿电力生产管理全过程的目的,较好地体现了电力生产以可靠性为中心的理念,同时,发挥了可靠性管理指导并服务于生产的重要作用。
