基于变时段的线性混合整数机组组合算法

陈 茜

（华北电力大学电气与电子工程学院，北京 102206）

0 引言

电力系统发电机的机组组合又称为开停机计划，研究的问题就是在保证系统安全的前提下如何合理地安排机组运行，使研究时段内的系统消耗费用最小［1-3］。当前随着电力市场机制的实施和电力系统规模不断加大，机组组合问题求解要求越来越高，人们开始了对这一问题的进一步探索和研究，应用线性混合整数规划法求解安全约束机组组合问题就是近年来的一个重要的研究方向［4-6］。文献叙述了美国PJM电力系统中采用混合整数规划法求解考虑市场出清价和安全约束的机组组合问题，回顾了混合整数规划法的发展历程，在实际系统测试中对比了混合整数规划法和拉格朗日松弛法的优劣。

一般机组组合问题研究周期为日到周的时间长度，以小时作为最小时段单位。在求解大规模电力系统机组组合时，由于部分约束个数随研究机组数时段数成倍增长，在机组时段数目较大时导致计算量过大计算时间很长。为此提出了根据不同简化原则对多时段机组组合问题，采用变时段技术减少时段数量进而减少了每次线性规划的计算规模和总体的计算量。算例分析*的结果表明，该方法快速有效，适合求解多时段电力系统机组组合问题。

1 算法模型

1.1 目标函数

机组组合的目标函数可以写为如下形式：

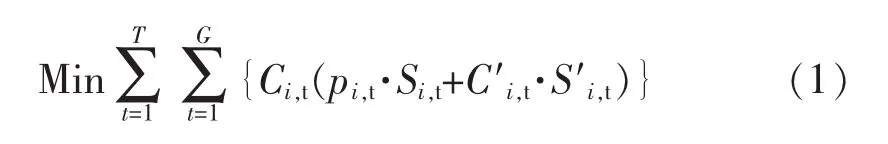
式中，T为研究时段数；G为发电机组数；Pi，t为机组i在时段 t内发电功率；Si，t为机组i在时段t内的状态（0或1）；Ci，t（pi，t）为第i台发电机第t时段的发电费用；C′i，t为机组i第t时段的启机费用；S′i，t为机组i在时段t内启机标志（0或1）。

1.2 约束条件

1）系统功率平衡约束。

式中，i=1，2，…G；t=1，2，…，t；PD，t为时段t内系统负荷。

2）机组功率约束。

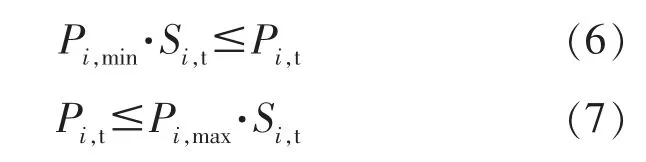
式中，i=1，2，…G；t=1，2，…，T；Pi，min为机组i发电功率下限；Pt，max为机组 i发电功率上限。

3）机组最小开机/停机时间约束。

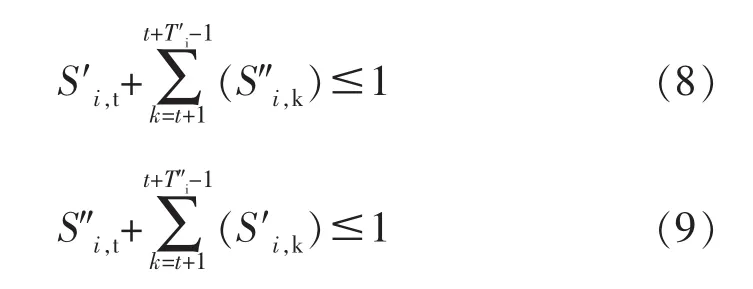
式中，i=1，2，…G，t=1，2，… T；T′i/T″i为机组i最小开 /停机时间；S′i，k/S″i，k为机组i在时段k启 /停机标志。

4）机组功率升降速度约束。

式中，i=1，2，…NG，t=1，2…，NT；Ri，t/Di，t为机组i在t时段爬坡率（向上、向下）极值。

5）网络功率约束。

这里考虑的网络约束为某一线路的功率约束或者系统中某一断面割集的功率约束。

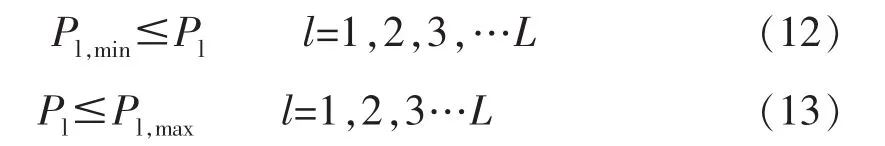
式中，Pl为支路 的有功潮流功率；l为受约束的支路号；Pl，min/Pl，max为第l条线路功率下限 /上限；L为支路总数。

2 变时段技术的应用

2.1 变时段技术原理

求解大规模多时段机组组合时会产生整数变量维数过多导致计算时间过长的问题，故需要根据一定的原则减少时段数量降低变量维数。变时段技术的思路是：精细划分重点关注的计算时段，合并简化其他非重点时段，同时处理简化时段对目标函数和约束条件的影响。时段的划分可以人为指定也可以按照负荷特性 （如负荷变化率）来进行。对1周（168h）机组组合问题尝试了以下3种时段划分。

方法1：不简化时段数，每小时为1时段共168时段。

方法2：按照1周负荷变化规律，将一周时间分为4个时段：A：周一0时至周一12时；B：周一13时至周五12时；C：周五13时至周五24时；D：周六0时至周日24时。对于A段负荷每小时作为1个时段，共12时段；B段负荷共4天96 h，可以根据计算精度的要求分别化为24时段或者48时段求解；对于C段负荷每小时作为1个时段，共12时段；D段负荷共2天48 h，可以根据计算精度的要求分别化为12时段或者24时段求解。这样168 h共分为12+24+12+24=72时段。

方法3：按照人为指定的方式，重点计算前3天各机组的状态和发电功率，将168 h分为24+24+24+12+12+12+12=120，此时前3天每小时为1个计算时段，后4天每两小时为一个计算时段，将1周划分为120个时段。

2.2 负荷的变化

研究时段发生变化后，同样是一个时段但是代表的时间长度却不相同，这样与时间段对应的系统负荷曲线也需要相应变化。在方法2中对不同天的同一时间的负荷进行合并，如表1；在方法3中采用了将不重点的连续几个时段合并为一个时段的方法，如表2。时段合并时采用平均负荷的计算方法，即变化时段的功率取对应时段的功率平均值。

表1 时段变化后的功率数值

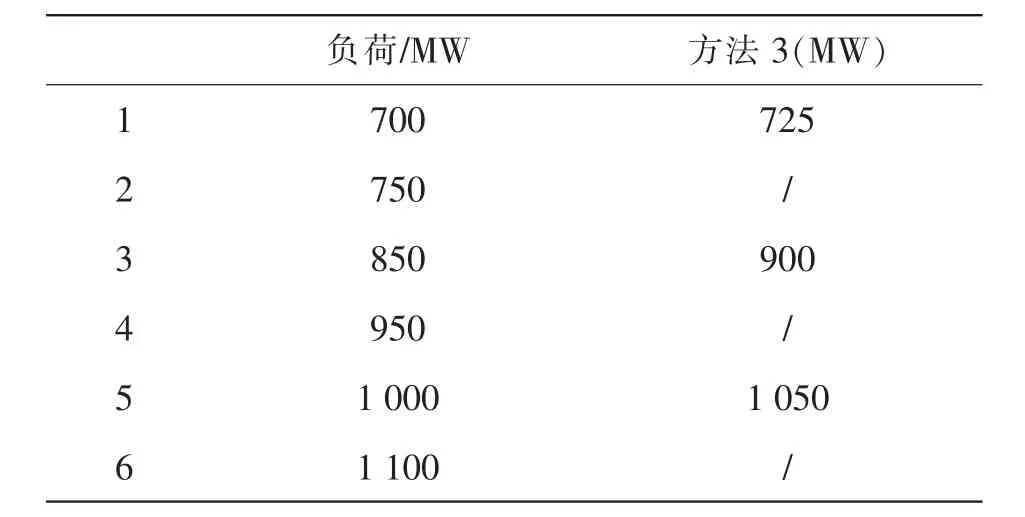
表2 时段变化后的功率数值

2.3 目标函数的变化

研究时段发生变化后，同一时段代表的时间长度不相同，这样与时间段相关的目标函数的表达形式也需要相应的变化。

式中，Bi为变时段后的第i时段发电费用，B′i为最小单位时段的第i时段发电费用，Nm为变时段后与最小单位时段的倍数。

2.4 约束的变化

研究时段发生变化后相关的约束条件也需要相应的变化。

1）机组最小开机/停机时间约束。

由于变时段后不同时段代表的时间长度发生变化，故需将原始的机组开停机时间折算到新的时段数，如：一台最小开机时段为10的机组，在采用第3种划分时段方法时其开停机时段如表3所示。

表3 变化时段的开停机时段数

2）对于方法2，由于简化了整天的时段，无须作此变换。由于时段变化后不同时段代表的时间长度发生了变化，故机组功率升降速度约束也需要相应改变。

式中，Ri，t为变时段后的第i机组t时段机组功率调整量的限制，R′i，t为最小单位时段的第i机组t时段机组功率调整量的限制，Nm为变时段后与最小单位时段的倍数。同上方法2此时不须变换。

3 计算分析

下面针对10机168时段（一周）系统变时段机组组合进行测试分析。机组及负荷数据参见文献附录，168时段负荷数据是将24时段数据重复7次得到。4种不同时段数计算数据如表4所示。

表4 计算结果统计表

从表4中可以看出，使用变时段技术后3次计算结果差异很小分别为0.027%和0.005%，而计算时间仅为以前的15.17%和40.12%。计算时间的大量缩减有两方面的原因：一方面是由于时段数减少导致计算次数的减少即线性规划计算次数分别为方法1的44.41%和81.97%；另一方面在每次计算负荷分配时计算规模也大为减少即求解线性规划时约束数目和非零元素个数也大为减少。

此外在采用变时段技术时，由于对被简化时段采用了平均负荷的处理办法，被简化时段与被合并时段的差值越大误差就会越大，因此在考虑时段的合并时尽量选择负荷变化较小的时段简化合并。

4 总结

电力系统机组组合问题的突出难点就在于整个系统计算量过大。针对多时段电力系统机组组合求解的特点在线性混合整数规划法的基础上提出了变时段技术的应用，该方法精细划分重点关注的计算时段，合并简化其他非重点时段从而削减计算规模减少计算次数。试验结果证明应用该技术可以在不严重影响计算精度的前提下快速、有效地缩短计算时间。