圆形分布资料平均角置信区间的Bootstrap方法实现

朱 凯 李 悦 刘伟新

医学上有些资料是用角度、季节或昼夜时间表示的，如心电向量的电轴、子宫颈口溃疡的位置、疾病发作时间、婴儿出生时刻等，这类用角度或时间表示的数据往往有周期性，形成圆形分布资料〔1〕。一组圆形分布资料，若有集中于某个时间或位置发生的倾向，则这一倾向可用平均角表示其集中位置。圆形统计分析的变量值是角度，所以作圆形统计分析时，计算平均角时需将非角度表示的原始数据转换为角度资料，令αi表示 α1，α2，…，αn角，¯α 表示样本平均角，是总体角均数的估计值。平均角的计算方法如下〔1〕:X=(∑

然而圆形分布的传统统计分析方法虽然能计算样本的平均角、估计角度的标准差，但由于无法获知平均角的确切分布故难以求出平均角的置信区间。因此本文引入Bootstrap非参数方法，利用大量的随机模拟求出平均角的置信区间。

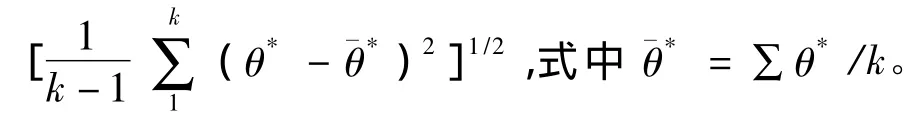
操作步骤

Bootstrap方法计算平均角的置信区间主要操作步骤:

1.根据实际观察到的原数据建立一个原始数据样本，含有n个观察值;

2.自原始数据样本 x=(x1，x2，…，xn)按有放回抽样的方法，抽得容量为n的样本x*=)(简称为Bootstrap样本);

3.相继地、独立地求出k个(k≥1000)容量为n的样本，i=1，2，…，k。对于第i个Bootstrap样本，按圆形分布资料方法计算平均角，，i=1，2，…，k(称为 θ的第i个Bootstrap估计);

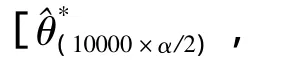
实例应用

现有某市492例精神分裂症患者复发发生时间，列于表1，欲估计复发时间的平均高峰角及平均高峰角的可信区间(α =0.95)〔3〕。

对该数据求平均发病时间的可信区间。每个Bootstrap样本含量n取492例。由文献〔2〕可知，重复10000次以上即可以得到相当好的估计。由于matlab软件执行效率较高，此处重复抽样100000次(k=100000)。每次抽样后得到一个圆形分布平均角，所以全部抽样完成后，一共能得到100000个平均角。对这100000个平均角由小到大排序后，找出2.5%和97.5%百分位数，从而得到平均角的95%的可信区间。对于Bootstrap方法计算平均角的可信区间，笔者编写了Matlab程序实现。程序如下，通过运行该程序，得到了平均角的点估计值为42.18，95%的可信区间为(31.41，52.95)。

表1 492例精神分裂症患者复发发生时间表

a=［609054533125241822283552］;%数据录入

讨 论

在总体分布未知，没有合适公式估计统计量或进行统计推断时，可以使用Bootstrap抽样来进行参数或非参数估计。在应用Bootstrap方法进行圆形分布资料平均角区间估计时需注意如下几个问题:

1.使用Bootstrap方法前须用Rayleigh’s test对圆形分布数据进行检验，以确保数据分布具有集中倾向〔4〕;

2.由于Bootstrap样本是在原数据中抽样获得的，如果已知样本含量太小，Bootstrap样本中重复抽得的数据就会增多，从而引起计算误差，故原数据中的样本含量应尽量大;

3.模拟误差来源于从Monte Carlo模拟抽样。理论上，无限次的模拟将会完全消除模拟误差，但显然这是不可能也没有必要的。因此确定模拟误差足够小并且计算可行的Bootstrap抽样次数是有效控制模拟误差的必要程序;

4.由于程序运行中要用到随机数，因此最终的结果有一定的误差，因此建议多次反复运行程序，待结果相对稳定时再下结论。

1.陆守曾.医学统计学.北京:中国统计出版社，2002，264-268.

2.盛骤等.概率论与数理统计.北京:高等教育出版社，2008，270-279.

3.田考聪.描述性统计分册.北京:人民卫生出版社，2004，108-110.

4.张圣勤.MATLAB教程及实训.北京:机械工业出版社，2008，118-125.

5.蔡雪亚，金丕焕，曹素华.用Bootstrap方法计算中位数的可信区间.中国卫生统计，2002，19(3):185-186.