Auto-regressive模型在全国婴儿死亡率拟合中的应用
2011-05-23潍坊医学院预防医学系261053李晓妹刘晓冬李向云
潍坊医学院预防医学系(261053) 刘 松 李晓妹 刘 健 刘晓冬 李向云
婴儿死亡率〔1〕(infant mortality rate,IMR)是反映居民健康水平、社会经济及卫生服务水平和妇幼卫生服务质量的敏感性指标。据卫生部统计,我国的婴幼儿死亡率由 1991年的 50.2‰下降到2007年的15.3‰〔2〕,总体上呈下降趋势。但与世界上其他国家相比,我国的婴儿死亡率仍然较高〔3〕。本文利用Autoregressive模型拟合我国婴儿死亡率的变化趋势,在评价其效果的基础上探讨残差自回归模型在其他非平稳时间序列数据拟合中的适用性。
资料和方法
1.资料来源 本文所利用的数据为我国1991~2007年的婴儿死亡率,来源于国家卫生部《2008中国卫生统计年鉴》,数据真实可靠。
2.统计方法 运用Auto-regressive模型对我国1991~2007年婴儿死亡率数据序列进行拟合;应用SAS 8.2统计软件对资料进行统计学分析〔4〕。
3.Auto-regressive模型建模步骤
(1)确定性因素分解〔5〕
在自然界中,由确定性因素导致的非平稳,通常显示出非常明显的规律性,比如有明显的趋势或者有固定的变化周期,这种规律性信息通常比较容易提取,而由随机因素导致的波动则非常难以确定和分析。根据这种性质,人们经过长期的观察和实践,通常把序列分解为三大因素的影响:
①长期趋势波动,包括长期趋势和无固定周期的循环波动。
②季节性变化,包括所有具有稳定周期的循环波动。
③随机波动,除了长期趋势波动和季节性变化之外,其他因素的综合影响归为随机波动。
(2)残差自相关检验
①检验原理
确定性模型拟合好之后,我们要对该模型的拟合效果进行检验。
如果残差序列显示出纯随机的性质,即

就说明确定性模型拟合非常好,已经能够充分提取序列中的相关信息,我们不需要再对序列进行二次信息提取,分析结束。
反之,如果残差序列显示出自相关性,即

那就说明确定性模型拟合得不够精确,序列中的相关信息没有得到充分提取,我们应该对残差序列再次拟合,提取其中残存的相关信息,以提高模型拟合的精度。
②残差自相关检验:Durbin-Waston检验(简称DW检验)
下面以残差1阶自相关性检验为例介绍DW检验的原理。
原假设:残差序列不存在1阶自相关性,即
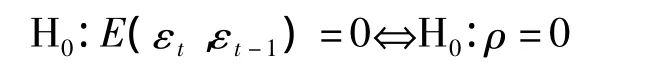
备择假设:残差序列存在1阶自相关性,即

构造DW检验统计量:
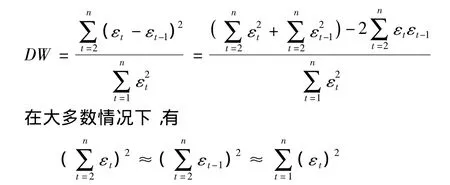
所以DW检验统计量近似等于:

即DW≅2(1-ρ),因为 -1≤ρ≤1,所以0≤DW≤4。当0<ρ≤1时,序列正相关;当 -1<ρ≤0时,序列负相关。
(3)Auto-regressive模型的建立
①确定自回归模型的阶数
根据模型的自相关图和偏自相关图,确定模型残差序列的自相关阶数。
②参数估计
根据原序列回归模型的口径,可以确定残差序列的值。单纯根据残差序列的值可以非常容易地确定残差自回归模型的口径。但是由于残差序列与序列回归值之间具有相关性,所以在将他们分开时不要忽略相关性的影响,否则会降低模型拟合的精度。所以,参数最优估计是在上述分析的基础上,确定回归模型的结构和残差自回归模型的阶数,将所有参数联合求解。
4.评价模型
根据确定系数R2对模型的拟合效果进行评价,以此判断该模型在对我国婴儿死亡率进行拟合的适用性和有效性。
结 果
1.平稳性检验

图1 我国1991~2007年婴儿死亡率序列时序图
时序图显示该时间序列有一个明显的随时间线性递减的长期趋势,同时又包含一定的随机信息,因此考虑使用残差自回归模型拟合该序列的发展。
2.纯随机性检验
纯随机性检验也称为白噪声检验,是专门用来检验序列是否为纯随机序列的一种方法。本文采用LB(Ljung-Box)统计量进行检验。检验结果显示,在6阶延迟下LB检验统计量为3.74(P<0.05),所以我们可以认为1991~2007年我国婴儿死亡率数据序列属于非白噪声序列。
3.Auto-regressive模型的建立
(1)确定性模型的建立

表1 普通最小二乘估计结果
从表1得出,输出的确定性模型为:Xt=108.0373-0.005345t+ μt
输出结果显示DW统计量的值等于0.5077,输出概率显示残差序列正相关(P<0.0001),所以应该考虑对残差序列拟合自相关模型。
(2)回归误差分析
进行回归误差分析时,采用逐步回归向后消除法。逐步回归向后消除报告显示除了延迟1阶和4阶的序列显著自相关外,延迟其他阶数的序列值均不具有显著的自相关性,因此延迟2阶、3阶和5阶的自相关项被消除。初步均方误差为1.2485,1阶残差自回归模型的参数φ1=-0.608073,φ2=0.438357。输出的自回归模型结果为:ut=0.608073ut-1-0.438357 ut-4+εt,具体结果详见表2。

表2 逐步回归向后消除法误差分析输出结果
(3)Auto-regressive拟合模型
该部分输出三方面的汇总信息:收敛情况、极大似然估计结果和回归系数估计,输出结果见表3:
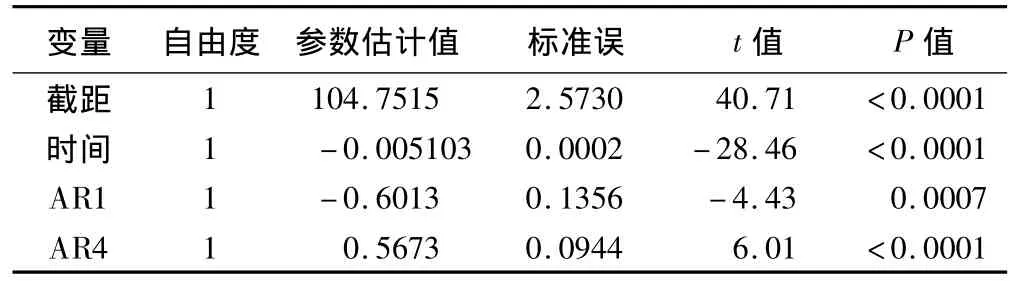
表3 最终拟合模型输出结果
由表3可得出,最终拟合我国婴儿死亡率得到的模型为:
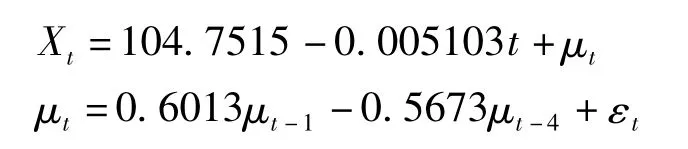
确定系数R2为0.9857,表明该模型所能解释的变异占全部变异的98.57%,比确定模型的决定系数R2=0.9627要大,证明模型拟合较好。
为了得到直观的拟合效果,利用SAS程序输出拟合效果图(图2)。

图2 Auto-regressive模型拟合效果图
拟合效果图中,星号表示实测值,实线表示Xt=104.75-0.005103t+μt的直线拟合,虚线表示整体模型 μt=0.6013μt-1-0.5673μt-4+ εt的曲线拟合。
讨 论
以往的研究多利用线性模型、指数模型等来探讨影响婴儿死亡率的相关因素〔6,7〕,如殷菲等采用径向基函数神经网络建立预测模型对婴儿死亡率进行预测;乔晓东等利用重复测量的多水平模型分析卫生Ⅷ项目县8年监测资料等。因为线性模型、指数模型、logistic回归模型等对资料的要求都比较严格,这些方法只能提取确定性信息,对随机性信息浪费严重。而Auto-regressive模型是一种拟合非平稳时间序列的方法,兼具了时间序列确定性分析和随机性分析的优点,它既能提取序列的确定性信息,又能提取其随机性信息。本文利用我国1991~2007年间婴儿死亡率的数据,时序图显示其具有长期变化和随机波动的非平稳特征,若仅用一般线性回归进行拟合,残差序列会存在自相关性,提示对序列信息的提取不充分。因此考虑选用Auto-regressive模型来拟合,效果较为理想。
由于医学、农业、工业、气象、经济等领域中的诸多现象都具有时间序列的特征,残差自回归模型的应用也日趋广泛。尤其在生物医学领域,如我国妇幼卫生监测网监测的出生缺陷率、孕产妇死亡率以及多种传染病的发病率等都具有非平稳时间序列的特征,可利用残差自回归模型对其进行拟合和预测。因此,Autoregressive模型具有良好的应用和发展前景。
同时,本研究也存在一定的局限性。婴儿死亡率受到多方面的影响,如卫生资源的配置、卫生服务的利用、经济发展状况和居民收入等,并且各种因素对婴儿死亡率影响的程度、方式、途径等都有各自的特点。所以在Auto-regressive模型的推广应用中要慎重加以考虑,否则会致使结果可能出现一定的偏差。
1.黄书香.认真贯彻落实《两纲》指标,提高妇女儿童健康水平.中国妇幼保健,2007,22(19):2609-2610.
2.卫生统计年鉴,中华人民共和国卫生部.2009.
3.刘娅,叶运莉,袁萍.中国婴儿1991~2004年死亡率趋势及预测分析.现代预防医学,2007,34(16):3101-3105.
4.刘晓冬,景睿,孟祥臻,等.残差自回归模型及SAS程序实现.中国卫生统计,2008,25(5):550-551.
5.王燕.应用时间序列分析.北京:中国人民大学出版社,2005.
6.殷菲,潘晓平.基于径向基函数神经网络的婴儿死亡率预测模型.现代预防医学,2006,33(4):486-487.
7.乔晓东,吴擢春,高艳,等.卫生Ⅷ项目地区婴儿死亡率影响因素的多水平分析.中国卫生统计,2009,26(1):49-51.
附录:SAS程序

