考虑滞后作用的地面沉降阿尔蒙分布预测模型

冯 羽，马凤山，魏爱华，赵海军，郭 捷

（中国科学院工程地质力学重点实验室 中国科学院地质与地球物理研究所，北京 100029）

1 地面沉降预测研究现状

地面沉降是一种由多种因素引起的地面标高缓慢降低的环境地质现象，严重时会成为一种地质灾害。人类活动和地质作用是造成地面沉降的主要原因，其中过量抽取地下水是最主要的原因［1］。地下水开采导致水位下降是含水层系统流场变化的关键，也是地面沉降形成与发展的重要因素，地面沉降是渗流场变化及地层应力重分布的过程［2］。过量开采地下水造成的地面沉降多发生在大中城市，对人们的生产、生活、交通等影响极大，造成的损失和危害也大，成为一种严重的环境地质问题，影响和制约着当地国民经济的可持续发展。而且一般沉降范围比较大，沉降过程缓慢，所以早期一般引不起人们的重视。因此，对于地面沉降量的预测问题就具有十分重要的实际意义。

国内外地面沉降预测研究的各种模型，归纳起来可以分为确定性模型和随机性模型两大类。确定性模型是由地下水水流模型和沉降模型耦合在一起构成的数学模型，通过专业软件进行数值模拟预测。随机性模型是根据地面沉降量影响因素的多样性与不确定性，利用概率统计分析方法找出这些不确定性因素的规律，从而建立相应的随机模型。目前常用的随机模型主要有回归分析、灰色模型预测、时间序列、神经网络等［3－5］。

薛禹群指出地面沉降相对于地下水位变化的滞后作用是我国地面沉降方面未来需要解决的问题之一，提出如何用数学表达式来描述这种滞后现象是模拟这些地区地面沉降必须克服的一个难题［6］。许多学者对于沉降的滞后问题也进行了分析研究［7－8］。

滞后，即是沉降变形与水位下降的不同步。滞后是一个比较复杂的问题，它主要与蠕变有关，但也可能更复杂。含水层水位恢复后地面仍表现出继续沉降，这里可能包含有两种情况：一部分是含水砂层的蠕变导致含水层水位恢复后，沉降变形继续发生；另一部分是在水位差消失没有越流后，弱透水层在蠕变影响下的沉降。严格意义上说，弱透水层的次固结沉降不应该算作滞后，只有与蠕变有关的变形现象才是滞后［6］。

含水砂层蠕变的现象在现场监测和室内试验都得到了证明［9］。对于含水砂层蠕变的原因，McDowell和Lade等［10－11］从砂土颗粒沿粒间接触面的相互滑移和颗粒破碎两方面解释了砂土的蠕变机制，原来处于平衡状态的砂土中存在大小不等的孔隙，在荷载作用下颗粒接触面上的剪应力增加，颗粒沿接触面产生错动滑移，土颗粒首先充填到较大的孔隙中，大孔隙被充填后土粒运动空间减小、移动的剪阻力增加，土粒的滑移速率减小，因此，土粒达到新的平衡需要一定的时间。另外，在荷载作用下粒间接触力增加，可导致部分土颗粒破碎，破碎形成的细小颗粒填充到土的孔隙中，颗粒位置重新调整。这两个过程在宏观上都表现为砂土的变形随时间延长而增加，但变形速率不断减小，最后趋近于稳定。另外，由于抽取地下水引起土层中有效应力的变化要缓慢得多，这就使得长期抽水引起的砂土层的变形表现出显著的时间相关性［12］。

对于粘性土的蠕变其产生的机制在学术界有不同认识，一是认为蠕变即为土体的次固结，其产生原因或是土中水膜的变形和作用，或是土颗粒黏结变化导致的结构调整；二是认为蠕变与次固结还是有一定区别，不仅是指体积变化中骨架的蠕动和硬化，更是指剪切造成的一种变形［13］。但粘性土变形的时效特性取决于蠕变和固结的共同作用却是得到共识的。有的学者从微结构变化的角度了解蠕变特性的内在机制，利用微观定量化技术，对比原状软土与蠕变条件下土样的微观孔隙，从微观角度对蠕变机制进行解释［14］；有的学者通过设计室内试验来研究粘性土蠕变的内在机理［12－13，15］，并且都得到了一些很有意义的结论。

2 阿尔蒙分布滞后模型的建立

某些变量之间的滞后因果关系，往往随着时间间隔的延伸而逐渐减弱。计量学中几何分布滞后模型反映了变量的影响程度随滞后期的延长而按几何级数递减，模型为：

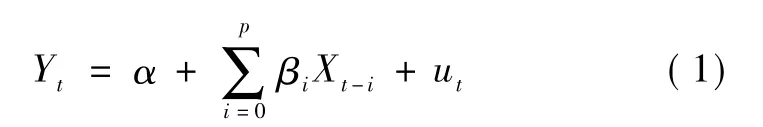
由于几何分布滞后模型中的随机扰动项通常存在一阶负相关关系，因此参数估计变得比较复杂。为解决几何分布滞后模型存在的问题，1965年阿尔蒙提出了利用有限多项式来减少待估参数个数以削弱多重共线性及参数估计中的自由度损失的有限分布滞后模型［16－17］。阿尔蒙分布滞后模型的基本原理，可以表示如下：

方程（1）是右边只含有外生变量及其滞后项的几何分布滞后模型，如果解释变量之间显然存在多重共线性，则不能用最小二乘法估计。为此，可将参数βi（i=0，1，2，…，k）的分布尽量地用一个关于 i的低级次多项式表示，这样就可以利用多项式减少模型中的参数。为此将βi分解为：

βi=α0+α1（i－¯p）+

α2（i－¯p）2+…+αq（i－¯p）q（q＜p）

p为滞后的期数，q是多项式的次数。此式称为阿尔蒙多项式变化。式中，i=0，1，2，…，p，并且

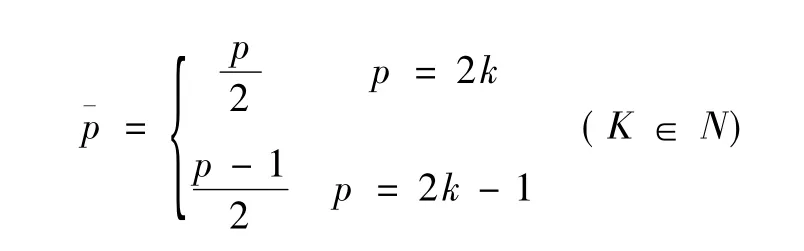
将每个βi参数都用一个阿尔蒙多项式表示，则几何分布滞后模型（1）即可改写为阿尔蒙分布滞后模型：

这样，式（2）相比较式（1）少了p－q个参数。

本文将采用阿尔蒙分布滞后模型来预测考虑地面沉降对地下水水位变化滞后作用的地面沉降量。

现收集到沧州地区连续11年时间内的地下水开采量、地下水水位以及地面沉降数据如下图1所示。

图1 沧州地面沉降数据Fig.1 LandsubsidencedatainCangzhou

分别用y和x两个序列来表示地面沉降量和地下水水位数据。首先，对 y和x两个序列分别取对数，因为时间序列取对数后可以减弱异方差性的影响，而且取对数后回归系数变为弹性，易于解释。同时考虑地下水水位对地面沉降量的作用在2年之后几乎消失，因此可以对模型采用远端限制条件。

对lnx和lny两个序列进行单位根检验，以判断两个时间序列的平稳性，进行单位根ADF检验结果如表1。

表1 单位根ADF检验结果Table1 ADFtestresults

经平稳性检验结果可知，lnx和lny两序列在1％的置信水平下都通过单位根ADF检验，都是平稳序列。

进行模型选择时，可以通过最小信息准则（AkaikeInformationCriterion）来确定滞后分布的长度，即滞后的期数。该项准则运用下式的统计量评价模型的好坏：AIC=－2L/n+2k/n，其中 L是对数似然值，n是观测值数目，k是被估计的参数个数，AIC的准则要求其值越小越好。因为，AIC的大小取决于L和k。k取值越小，AIC越小；L取值越大，AIC值越小。K小意味着模型简洁，L大意味着模型精确。因此AIC和修正的决定系数类似，在评价模型时兼顾了简洁性和精确性。

根据AIC信息准则以及对地面沉降滞后的理论认识，确定模型的滞后期数为3，即当年的地下水抽水作用只对未来三年的地面沉降量有影响，对其后地面沉降的影响暂且忽略。对lnx和lny两序列建立阿尔蒙分布滞后模型，预测模型方程如下：

可决系数R2=0.8023。

预测模型方程中，Yt表示第 t年的地面沉降量，Xt、Xt－1、Xt－2、Xt－3分别表示当年的地下水水位、去年的地下水水位、前年的地下水水位、大前年的地下水水位。其前面的系数，则表示该变量对当年地面沉降量的影响程度。可以看出，影响系数随着前推年数的增加是逐年递减的，符合实际情况。

模型中各参数均是在1％的显著性下通过t检验的，回归方程也通过F检验。对回归结果进行LM检验，证明模型不存在自相关问题。

计量学中规定平均绝对误差百分比（Mean AbsolutePercentageError-MAPE）的取值在0～5之间说明预测精度极高，本文阿尔蒙分布滞后模型的MAPE的值为3.64，说明模型预测效果非常好。西尔不等式系数TIC的取值范围是0～1之间且取值越小越好，本文取值0.02，也说明预测是十分理想的。由于模型滞后期选为3，因此预测曲线是从第4年开始的，模型预测结果见图2。

3 阿尔蒙分布滞后模型精度分析

采用目前非线性分析方法中比较常用的灰色GM（1，1）预测模型和神经网络预测模型的预测结果与阿尔蒙分布滞后模型的预测结果进行对比。

图2 预测值（LNYF）与真实值（LNY）的拟合曲线Fig.2 Fittingcurveofpredictive value（LNYF）andtruevalue（LNY）

为了提高预测精度，分别对这两种算法进行了相关处理。灰色GM（1，1）模型主要存在两方面的局限性。一是数据离散程度越大，即数据灰度越大，则预测精度越差［18］；二是模型的拟合序列为非齐次指数序列，需要原始数据具有明显的指数规律预测结果才够准确，因此不太适合后推年限较长的预测［3］。因此对沉降观测数据进行了归一化后取对数操作，弹性缩小了数据的增长速度，使模型预测的结果更加准确。对于神经网络预测，预测前先对沉降数据进行了归一化处理，以优化网络初始权值和阀值的选取。而且分别计算了选取不同个数中间层神经元个数时神经网络的误差，选取了网络误差最小的中间层神经元个数。灰色GM（1，1）模型与神经网络预测结果见图3、图4。

三种模型预测精度对比见表2。

表2 三种模型预测精度对比Table2 Predictionaccuracycomparisonofthreemodel

通过预测结果相对误差百分比的对比可以发现，阿尔蒙分布滞后模型的预测精度要明显高于灰色GM（1，1）预测模型，与神经网络预测模型的预测精度相当，但神经网络预测精度的起伏较大，而阿尔蒙分布滞后模型的预测精度一直保持较高的预测精度，比较平稳。

图3 灰色GM（1，1）模型预测值拟合曲线Fig.3 FittingcurveofGM（1，1）modelprediction

图4 神经网络预测值拟合曲线Fig.4 FittingcurveofNNmodelprediction

4 结论

地面沉降相对于地下水水位变化的滞后性的机理问题目前仍在研究当中，但地面沉降的发展具有时效性却是得到共识的。本文基于这种滞后作用的考虑，建立了地面沉降的阿尔蒙分布滞后模型，并以沧州地区的地面沉降为算例进行预测；分别用灰色GM（1，1）预测模型和神经网络预测模型进行计算，与阿尔蒙分布滞后模型的计算结果进行精度对比分析。结果表明，阿尔蒙分布滞后模型的预测效果非常好，平均绝对误差百分比MAPE值仅为3.64。通过精度对比，阿尔蒙分布滞后模型相较于另外两种方法均有提高。因此，阿尔蒙分布滞后模型可以应用到地面沉降预测领域中去。

［1］薛禹群，张云，叶淑君.中国地面沉降及其需要解决的几个问题［J］.第四纪研究，2003，23（6）：585－593.XUEYuqun，ZHANGYun，YEShujun.Landsubsidence andissuestobesolvedinChina［J］.ChineseQuaternary Research，2003，23（6）：585 －593.

［2］龚世良.上海地下水流场变化及对地面沉降发展的影响［J］.水资源与水工程学报，2009，20（3）：1－5.GONGShiliang.Changeofgroundwaterseepagefieldand its influence on developmentofland subsidence in Shanghai［J］. JournalofWaterResources ＆Water Engineering，2009，20（3）：1－5.

［3］陈鹏宇.地面沉降模拟计算的灰色离散 GM（1，1）模型［J］.地质灾害与环境保护，2009，20（4）：101－105.CHENPengyu.DiscreteGM（1，1）forgroundsubsidence simulation［J］. Journalof GeologicalHazards and EnvironmentPreservation，2009，20（4）：101 －105.

［4］李红霞，赵新华，迟海燕，等.基于改进 BP神经网络模型的地面沉降预测及分析［J］.天津大学学报，2009，42（1）：60－64.LIHongxia，ZHAOXinhua，CHIHaiyan，etal.Prediction andanalysisoflandsubsidencebasedonimprovedBP neuralnetworkmodel［J］.JournalofTianjinUniversity，2009，42（1）：60 －64.

［5］马保卿，张荫.灰色线性回归组合模型在地面沉降预测中的应用［J］.铁道勘察，2008（5）：20－22.MABaoqing，ZHANGYin.ApplicationofsyntheticModel ofgreytheoryandlinearregressioninforecastingforground subsidence［J］.RailwayInvestigation，2008（5）：20 －22.

［6］薛禹群.我国地面沉降模拟现状及需要解决的问题［J］.水文地质工程地质，2003，（5）：1 －5.XUEYuqun.Presentstatusofmodelinglandsubsidencein Chinaandproblemstobesolved［J］.Hydrogeologyand EngineeringGeology，2003（5）：1 －5.

［7］陈崇希，裴顺平.地下水开采 －地面沉降模型研究［J］.水文地质工程地质，2001，28（2）：5 －8.CHENChongxi，PIEShunping.Researchonmodelingof groundwaterwithdrawingcouplingwithlandsubsidence［J］.ChineseHydrogeology＆ EngineeringGeology，2001，28（2）：5－8.

［8］王光亚，于军，吴曙亮，等.常州地区地面沉降及地层压缩性研究［J］.地质与勘探，2009，45（5）：612 －620.WANGGuangya，YU Jun，WU Shuliang，etal.Land subsidenceandcompressionofsoilLayersinChangzhou area［J］.GeologyandExploration，2009，45（5）：612 －620.

［9］张云，薛禹群，施小清，等.饱和砂性土非线性蠕变模型试验研究［J］.岩土力学，2005，26（12）：1869 －1873.ZHANGYun，XUEYuqun，SHIXiaoqing，etal.Studyon nonlinearcreepmodelforsaturatedsand［J］.Rockand SoilMechanics，2005，26（12）：1869－1873

［10］MCDOWELLGR.Micromechanicsofcreepofgranular materials［J］.Geotechnique，2003，53（10）：915 －916.

［11］LADEPV，LIUCT.Expimentalstudyofdrainedcreep behaviorofsand［J］.JournalofEngineeringMechanics，1998，124（8）：912－920.

［12］张云，薛禹群，吴吉春，等.上海砂土蠕变变形特征的试验研究［J］.岩土力学，2009，30（5）：1226 －1236.ZHANG Yun，XUE Yuqun，WU Jichun，etal.ExperimentalresearchoncreepofShanghaisands［J］.RockandSoilMechanics，2009，30（5）：1226 －1236.

［13］陈晓平，周秋娟，朱鸿鹄，等.软土蠕变固结特性研究［J］.岩土力学，2007，28（S）：1 －9.CHENXiaoping，ZHOUQiujuan，ZHUHonghu，etal.Researchoncreepandconsolidationcharacteristicsofsoft soil［J］.RockandSoilMechanics，2007，28（s）：1－9.

［14］张先伟，王常明，李军霞，等.蠕变条件下软土微观孔隙变化特性［J］.岩土力学，2010，31（4）：1061 －1067.ZHANGXianwei，WANGChangming，LIJunxia，etal.Variationcharacteristicsofsoftclaymicroporeincreep condition［J］.RockandSoilMechanics，2010，31（4）：1061－1067.

［15］陈晓平，朱鸿鹄，张芝芳，等.软土变形时效特性的试验研究［J］.岩石力学与工程学报，2005，24（12）：2142－2148.CHENXiaoping，ZHUHonghu，ZHANGZhifang，etal.Experimentalstudyontime-dependentdeformationofsoft soil［J］.Chinese JournalofRock Mechanics and Engineering，2005，24（12）：2142 －2148.

［16］杜凯，李均立，卞平平.原油价格对天然橡胶价格影响的分布滞后模型［J］.中国市场，2010（20）：114－118.DUKai，LIJunli，BIANPingping.Thelagmodelofnatural rubberpricesimpactedbycrudeoilprice［J］.Chinese Market，2010（20）：114－118.

［17］黄伟力.基于阿尔蒙分布滞后模型的投资利润弹性估计［J］.统计与决策，2008（11）：19－20.HUANGWeili.Theelasticityestimatedofinvestment returnsbasedonAlmonlagmodel［J］.Decision－making andstatistical，2008（11）：19－20.

［18］刘棠洪，周俊，朱庆川.改进的灰色预测模型在地面沉降预测中的应用［J］.地质灾害与环境保护，2007，18（3）：104－107.LIUTanghong，ZHOUJun，ZHUQingchuan.Application ofimprovedgreymodelinlandsubsidenceforesting［J］.Journal of Geological Hazards and Environment Preservation，2007，18（3）：104 －107.